基于改进循环观测的线性预测语音压缩感知

徐皓波,于凤芹

(江南大学物联网工程学院,江苏无锡214122)

基于改进循环观测的线性预测语音压缩感知

徐皓波,于凤芹

(江南大学物联网工程学院,江苏无锡214122)

利用语音信号线性预测残差的稀疏性特点可对语音信号进行压缩感知,但需要信号的线性预测系数来构造稀疏变换矩阵,从而增加预测系数传输的数据量。为此,提出将线性预测系数存入对角阵向量中构造循环矩阵,由此得到循环观测矩阵,再对语音信号进行观测。提取该循环矩阵中的线性预测系数构造残差域稀疏变换矩阵,利用正交匹配追踪算法对观测信号进行重构。仿真实验结果表明,与传统线性预测方法相比,该方法减少了3.9%以上的数据量,且比将高斯随机矩阵作为观测矩阵的方法具有更高的帧平均重构信噪比。

线性预测;压缩感知;循环观测;残差域稀疏变换;正交匹配追踪;重构信噪比

1 概述

压缩感知是近年来兴起的一种信号处理技术,它利用信号在某个变换域的稀疏性,将原始信号的全部信息投影在随机观测矩阵上,得到一个维数较小的观测向量,通过优化算法最终恢复原信号［1］。信号的稀疏性是压缩感知的前提和基础,直接关系着压缩程度和恢复效果［2］。由于语音信号在DCT域是近似稀疏的,目前有关DCT域语音压缩感知进行了广泛的研究。文献［3］利用语音信号的线性预测残差具有一定的稀疏性,提出基于线性预测的语音压缩感知方法,重构效果比DCT域方法更好。文献［4］提出用差分变换提高线性预测残差的稀疏性,从而提高重构效果。文献［5］提出使用线性预测模型和DFT模型组成的融合字典,为每帧语音提供最适合的原子,获得更好的重构质量。使用线性预测方法进行语音的压缩感知时,需要利用每帧语音的线性预测系数来构造稀疏变换矩阵,额外传输每帧信号的预测系数增加了数据量。文献［6］提出用训练语音的预测系数聚类构造过完备字典,从而不需要测试语音预测系数。而文献［7］提出若前后两帧相关性较强则可以使用前帧语音的预测系数代替后帧,从而减少预测系数的计算和传输。减少传输线性预测系数对线性预测语音压缩感知十分关键。

本文以线性预测压缩感知方法为基础,以减少线性预测系数的数据传输量为出发点,对分帧后的各帧语音信号进行线性预测分析;将预测系数平均分布在循环矩阵特征值向量中,利用傅里叶变换的性质构造循环矩阵,从而实现对语音信号的循环观测;从循环矩阵中提取出各帧信号的线性预测系数来构造对应的稀疏变换矩阵,减少预测系数的额外传输;通过OMP正交匹配追踪算法［8］重构信号。

2 线性预测语音压缩感知原理

2.1 压缩感知基本原理

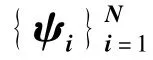
2.2 基于线性预测的稀疏表示

线性预测分析利用了若干个语音取样的过去值的加权线性组合来逼近语音取样的现在值。通过使实际语音抽样和线性预测抽样之间差值的平方和达到最小值,能够唯一决定一组线性组合的加权系数,即线性预测系数。对于一个语音信号取样值x(n),在一定的线性预测系数ai下,可以根据信号过去p个取样值的线性组合来逼近:

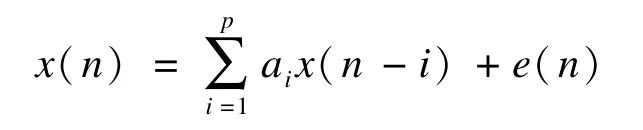
其中,e(n)为线性预测分析的残差。

由于残差e=［e(1),e(2),…,e(N)］T是通过最小均方误差准则得出的,理想情况下残差包含很多零值,具有稀疏性,因此可以利用残差域对语音信号进行稀疏表示。假设语音信号表示为:x=［x(1),x(2),…, x(N)］T,利用线性预测系数可以构成一个矩阵A:

使得e=Ax,则语音信号可以表示为xx=A-1e。根据线性预测分析理论,浊音的残差是以基音周期为周期的单位脉冲序列,有较好的稀疏性,而清音稀疏性较差［4］。

2.3 预测系数循环矩阵的构造

为了使压缩感知更具实用性,文献［11］利用结构化的Toeplitz和循环矩阵来构造观测,通过对矩阵的分析研究证明了其可行性。假设矩阵C是一个基本的循环矩阵,由于循环矩阵的特殊结构,只需矩阵的一列元素就能获得矩阵全部的信息,大大节省了存储计算成本。根据傅里叶变换的应用延伸,可由傅里叶变换矩阵F和对角阵Λ=diag(λ)通过公式C=F-1ΛF得到一个N×N维的循环矩阵［12］。

然后从循环矩阵中随机抽取M行组成一个M× N的矩阵,即可作为压缩感知中的观测矩阵。在利用傅里叶变换构造循环矩阵时,特征值对角阵元素直接影响循环矩阵中的元素,从而影响到循环观测矩阵能否满足投影采样时所需的非相关性,一般对角阵中元素通常使用正负1的伯努利分布。因此,构造循环观测矩阵只需要传输一个长度为N的随机分布向量,由此得到N×N维的循环矩阵,再得到M×N的观测矩阵。而在传统的线性预测语音压缩感知研究中,如何减少预测系数的传输一直是研究的重点,无论是训练过完备字典还是利用帧间相关特性对预测系数进行重复利用,都在预测系数本身考虑。本文却是从另一个角度,利用傅里叶变换构造循环矩阵的性质,将各帧语音的线性预测系数存入特征值对角阵Λ=diag(λ),即确定对角阵固定位置的取值为一个线性预测系数,该对角阵各特征值组成的向量如下式所示:

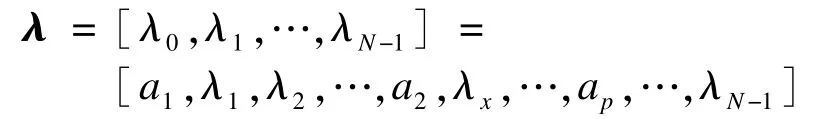
通过包含预测系数的对角阵构造循环矩阵,从而对语音进行循环观测。确定预测系数在对角阵中的位置,就可以由循环矩阵中还原出线性预测系数,减少了构造稀疏变换矩阵时预测系数的数据量。

3 算法实现步骤

本文关于循环观测改进的线性预测语音压缩感知的具体步骤如下:

(1)将语音信号进行分帧处理,对各帧信号进行线性预测分析,得到预测系数ai。

(2)将预测系数ai以固定位置赋值于呈正负1的伯努利分布的向量λ=［λ0,λ1,…,λN-1］中。

(3)由傅里叶变换矩阵F和对角阵Λ=diag(λ)通过公式C=F-1ΛF得到一个包含预测系数信息的N×N维循环矩阵。从N×N维方阵中随机抽取M行构成M×N维的矩阵的循环观测矩阵Φ。

(4)由循环矩阵C反推出该帧信号的线性预测系数,构造出对应该帧的残差变换矩阵A。

(5)各帧信号x(i)经过循环观测矩阵Φ投影得到观测y(i),通过OMP算法重构信号,字典为D=ΦA-1,得到残差系数e的估计e′,从而得到x(i)的重构x′(i)=A-1e′。

(6)由各帧信号合成得到原始语音的重构。

4 仿真实验与分析

实验1主要研究了语音信号在线性预测残差域下稀疏性及重构效果。给定一段16 kHz的男声发音为“大发”的汉语语音,从其中的韵母a和声母f中分别截取一帧信号分别代表浊音和清音,帧长为320个采样点。图1所示为该2帧信号时域波形及其在线性预测残差域下的稀疏系数分布。

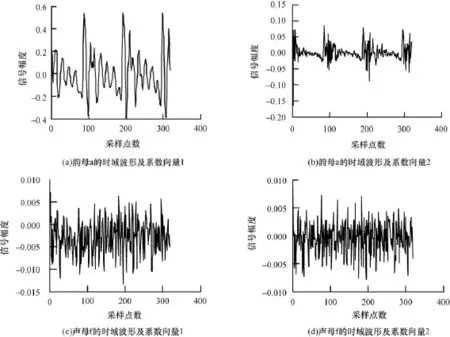
图1 浊音帧与清音帧的时域波形及线性残差域稀疏性

观察图1发现浊音帧的时域波形具有明显的周期性,且振幅较大,在线性预测残差域上展现出较好的稀疏性;而清音帧的时域波形类似于白噪声,且振幅较小,没有明显的周期性,在线性预测残差域上稀疏性较差。对整段语音线性预测残差域的稀疏表示下进行压缩感知重构,使用高斯随机矩阵进行观测,压缩比r=M/N分别取0.8和0.6,线性预测系数取10阶,利用OMP算法进行恢复,以各帧重构信噪比进行比较。

图2所示为基于线性预测语音压缩感知方案的各帧信噪比情况。观察图2发现部分帧的重构信噪比急剧下降,分析语音可以发现这些帧都属于清音帧,稀疏性较差,故重构质量不佳。但由于语音的重要信息大多数都在浊音部分,清音重构虽然存在较大误差也可以忽略;浊音帧部分重构信噪比则相对比较理想。而随着压缩比的提高,各帧信噪比也相应提高。

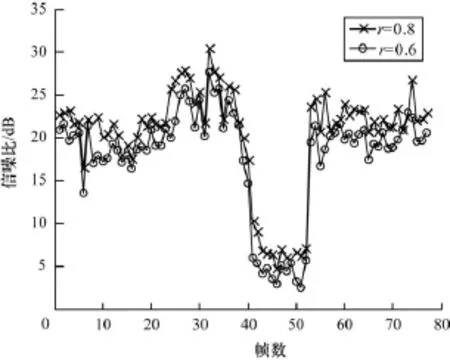
图2 不同压缩比线性预测残差域的各帧重构信噪比

实验2研究了在线性预测语音压缩感知下使用高斯随机矩阵和预测系数循环观测矩阵的重构效果及传送数据量。首先对语音进行分帧,对各帧语音进行10阶的线性预测分析,得到预测系数,再由预测系数构造循环矩阵,从而得到循环观测矩阵,分别以不同压缩比进行观测,计算各帧信号的重构信噪比,然后得到帧平均重构信噪比。图3为不同压缩比下使用2种观测矩阵的平均重构信噪比情况。

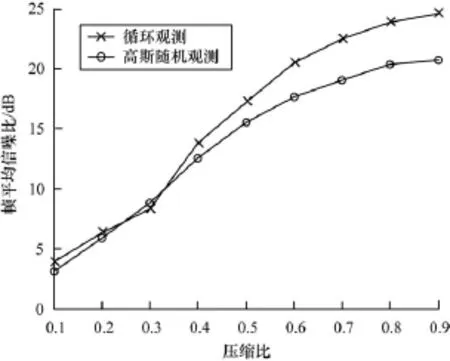
图3 2种观测矩阵的帧平均重构信噪比

表1为预测阶数为10时不同压缩比下节省数据量的比例,数据量=(观测数目 +预测阶数)×帧数。

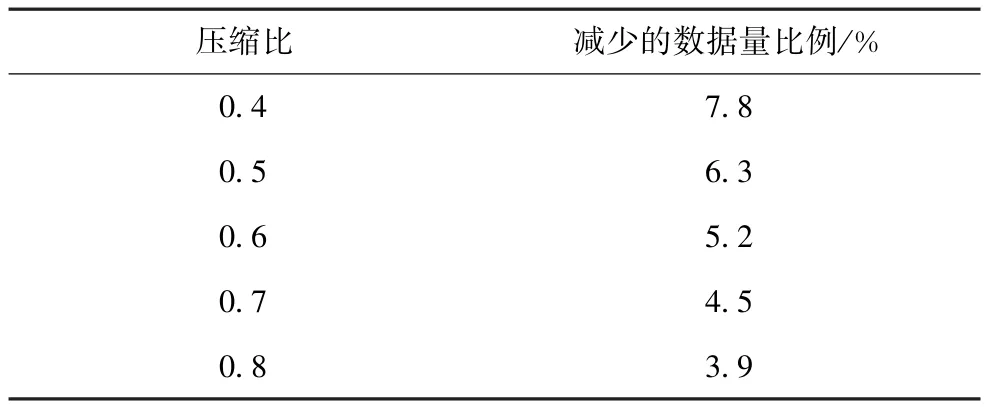
表1 各压缩比和减少的数据量比例

预测系数循环观测在大多数压缩比情形下平均重构信噪比均高于高斯随机矩阵观测,不仅提高重构效果,还从另一角度减少了传递预测系数的步骤,突破了传统线性预测的语音压缩感知的局限,减少数据量比例达到3.9%以上,增强了实用性。

5 结束语

本文提出使用包含预测系数信息的循环矩阵构造观测,在构造观测矩阵的同时可以提取预测系数,不需要额外地传输预测系数,提高了线性预测压缩感知方法的实用性。仿真实验结果证明了线性预测的语音压缩感知方法有较好的重构效果;使用预测系数循环矩阵构造观测,不仅减少了预测系数的传递,而且比起高斯随机矩阵有更高的平均信噪比。因此,选择一种合适的稀疏表示直接关系到信号的重构效果,而寻找更为有效快速的重构算法也是今后研究的重点。

［1］ Donoho D.Compressed Sensing［J］.IEEE Transactions on Information Theory,2006,52(4):1289-1306.

［2］ Candes E J,Romberg J.Sparsity and Incoherence in Compressive Sampling［J］.Inverse Problems,2007,23 (3):969-985.

［3］ Giacobello D,Christensen M G,Murthi M N.Retrieving Sparse Patterns Using a Compressed Sensing Framework: Applications to Speech Coding Based on Sparse Linear Prediction［J］.IEEE Signal Processing Letters,2010,17 (1):103-106.

［4］ 高 悦,陈砚圃,闵 刚,等.基于线性预测分析和差分变换的语音信号压缩感知［J］.电子与信息学报, 2012,34(6):1408-1413.

［5］ Wang Yue,Xu Zhixing,Li Gang,et al.Compressed Sensing Framework for Speech Signal Synthesis Using a Hybrid Dictionary［C］//Proc.of the 4th International Congress on Image and Signal Processing.［S.l.］:IEEE Press,2011:2400-2403.

［6］ 孙林慧,杨 震,季云云,等.基于过完备线性预测字典的压缩感知语音重构［J］.仪器仪表学报,2012,33 (4):743-749.

［7］ 赵 翠,周 遥,毛鑫萍,等.基于线性预测的自适应语音压缩感知［J］.杭州电子科技大学学报,2012,32 (4):13-16.

［8］ Pati Y C,Rezaifar R K.Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition［C］//Proc.of the 27th Annual Asilomar Conference in Signals,Systems and Computers.Pacific Grove,USA:［s.n.］,1993:40-44.

［9］ Tsaig Y,Donoho D.Extensions of Compressed Sensing［J］.Signal Processing,2006,86(3):533-548.

［10］ Emmanuel C,Terence T.Near Optimal Signal Recovery from Random Projections:Universal Encoding Strategies［J］.IEEE Transactions on Information Theory,2006,52 (12):5406-5425.

［11］ Holger R. Circulant and Toeplitz Matrices in CompressedSensing［C］//Proc.ofSPARS'09.Saint Malo,France:［s.n.］,2009.

［12］ Rao K R,Kim D N,Hwang J J.Fast Fourier Transform: Algorithms and Applications［M］.Arlington,USA: Springer,2010:34-37.

编辑 顾逸斐

Linear Predictive Speech Compressed Sensing Based on Improved Circulant Observation

XU Haobo,YU Fengqin
(School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China)

The sparsity of the linear predictive residual of speech signal can be used in the speech compressed sensing, but needs the predictive coefficients of the signal to build sparse transformational matrix increasing the data.This paper proposes to save the linear predictive coefficients into diagonal matrix in order to build circulant matrix,and measures the speech signal in circulant way,extracts the linear predictive coefficients from circulant matrix to build sparse transformational matrix in residual domain,and reconstructs the speech with Orthogonal Matching Pursuit(OMP) algorithm.Simulation experimental result shows that,using circulant measure built by predictive coefficients decreases 3.9%data more than the original linear predictive method,and has higher reconstruction signal to noise ratio per-frame than the Gaussian random matrix as measure matrix.

linear prediction;compressed sensing;circulant observation;sparse transformation in residual domain; Orthogonal Matching Pursuit(OMP);reconstruction signal to noise ratio

1000-3428(2014)11-0278-04

A

TN911.7

10.3969/j.issn.1000-3428.2014.11.055

国家自然科学基金资助项目(61075008)。

徐皓波(1988-),男,硕士研究生,主研方向:语音信号处理;于凤芹,教授。

2013-10-10

2013-11-29E-mail:xhb316@qq.com

中文引用格式:徐皓波,于凤芹.基于改进循环观测的线性预测语音压缩感知［J］.计算机工程,2014,40(11):278-281.

英文引用格式:Xu Haobo,Yu Fengqin.Linear Predictive Speech Compressed Sensing Based on Improved Circulant Observation［J］.Computer Engineering,2014,40(11):278-281.