基于M-H采样的快速反向微分进化算法
2014-06-07涂维维葛洪伟杨金龙袁运浩
涂维维,葛洪伟,杨金龙,袁运浩
(江南大学物联网工程学院,江苏无锡214211)
基于M-H采样的快速反向微分进化算法
涂维维,葛洪伟,杨金龙,袁运浩
(江南大学物联网工程学院,江苏无锡214211)
反向微分进化(ODE)算法基于反向优化对种群进行初始化更新以保持种群多样性。但该算法中反向个体容易偏离全局最优个体,不能很快达到全局最优,在函数优化过程中收敛速度慢且容易陷入局部最优。为此,提出一种基于M-H采样的快速反向微分进化算法。M-H采样用于ODE算法的变异操作,满足马尔可夫链可逆条件。马尔可夫链的一步转移概率根据个体等级分配的选择概率进行计算,既能选择最优个体,又能寻找优化方向并保持种群多样性。仿真结果表明,M-H采样得到的个体具有马尔可夫链平稳分布特性,该算法在单峰函数和多峰函数优化中都能快速收敛,全局和局部搜索性能达到平衡,具有较高的搜索精度及较好的鲁棒性。
微分进化算法;反向微分进化算法;转移概率;平稳分布;马尔可夫链蒙特卡洛;反向学习
1 概述
进化算法是一种模拟生物进化过程求解优化问题的启发式自适应人工智能技术。1995年Storn和Price等人提出微分进化(Differential Evolution, DE)[1-2]算法,其主要特点是算法简单、收敛速度快、可调参数少、鲁棒性好,相对于其他优化算法有较强的全局收敛能力和稳定性。变异操作是微分进化的核心操作,对微分进化的影响很大,文献[3]是关于微分进化算法的参数和变异策略的综述和应用。近年来DE成功应用于不同领域,如:工程优化设计,数字滤波器设计,图像处理,数据挖掘,多传感器融合等。但是微分进化算法在高维多峰函数优化中容易陷入局部最优,收敛速度慢、优化性能不稳定。针对DE算法的缺陷,许多学者提出了很多改进方法,如文献[4]采用自适应控制参数来提高微分进化算法的收敛性能,但是收敛速度依然较慢;文献[5]在文献[4]的基础上增加了种群规模减少机制和3个变异策略,改善收敛速度和DE算法的鲁棒性,但是算法性能不稳定,易于陷入局部最优;文献[6]引入基于排序的变异,将种群个体进行适应度排序后,进行迭代更新,维持局部搜索和全局搜索的平衡;文献[7]将种群分成多个子群,动态调整每个子种群的个体数目,增加子种群间个体信息交换,并且采用局部搜索和自适应方法,然而该算法参数较多,选择困难,且常由于参数选择不当导致性能不稳定;文献[8]提出一种分阶段的二次变异,提高算法的全局搜索能力,但增加了时间复杂度;文献[9]采用邻域变异方法,在某个设定的领域内取得变异的个体,这种方法易于陷入局部最优;文献[10]通过求反向种群来保持种群多样性,但是反向个体容易偏离全局最优个体,更新速率较慢,不能很快地达到全局最优。
本文采用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)思想,提出基于 Metropolis-Hastings(M-H)采样的算法用于反向微分进化(Opposition Differential Evolution,ODE)[10]算法(MHODE)的变异操作。M-H算法具有马尔可夫链的平稳性,所采样的个体具有平稳分布的特性,根据该采样进行变异操作,能使M-HODE算法的收敛速度加快,收敛趋于平稳。
2 微分进化和反向微分进化算法
2.1 微分进化算法


图1 DE算法流程
微分进化算法流程:
(1)初始化种群
在决策空间X内,用式(1)随机产生初始向量:
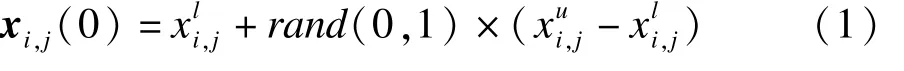
(2)变异操作
微分进化算法的差分向量与缩放因子相乘后跟基向量进行向量合成,一般采用DE/rand/1变异策略,变异操作的公式为:
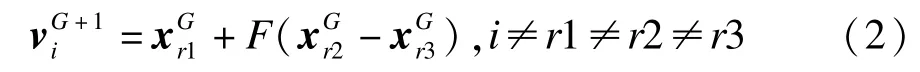
(3)交叉操作
对变异产生的新个体和当前个体进行交叉操作,以增加种群个体的多样性。经过交叉操作得到实验向量:

其交叉操作公式如下:
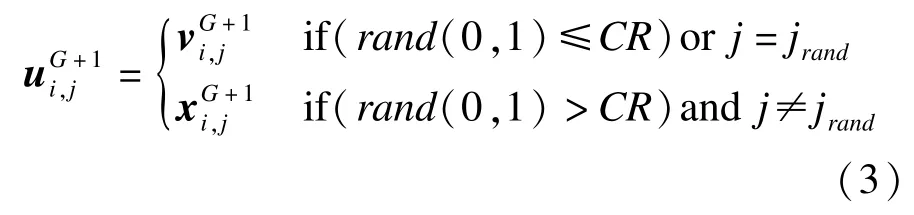
其中,j=1,2,…,D;CR∈[0,1]为交叉概率;jrand∈[1,D]为均匀选取的随机整数。
(4)选择操作
DE算法通过选择操作,对实验个体和当前个体进行适应度评价,根据式(4)决定候选个体是否取代当前个体。
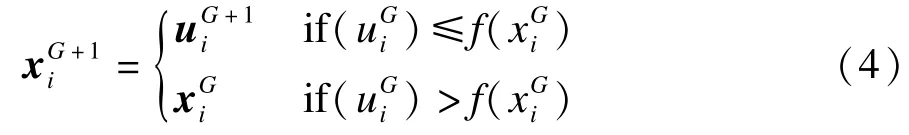
2.2 反向微分进化算法
2.2.1 反向学习理论
反向微分进化算法是基于反向学习(Oppositionbased Learning,OBL)理论的微分进化算法。OBL理论思想如下:
定义1(反向个体) 在多维空间R,p=(x1,x2,…,xD)是D维空间的一个个体,x1,x2,…,xD∈R,xi∈[a,b]∀i∈{1,2,…,D},式(5)求反向个体=。

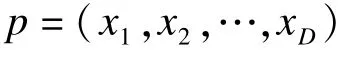
2.2.2 ODE算法步骤
ODE算法步骤具体如下:
步骤1 基于反向学习的种群初始化。
(1)随机产生均匀分布的种群Po,大小为NP。
(2)用定义1中的式(5)来计算Po中每一个个体的反向个体opoi,j=aj+bj-poi,j,使用反向优化方法从集合{po,Opo}中选NP个适应度最好的个体作为初始种群。
步骤2 根据迭代条件,对种群个体进行微分进化算法的变异、交叉、选择操作。
步骤3 随机反向代跳操作,若随机的rand(0, 1)<Jr(Jr是跳转概率),MINPj和MAXP
j分别是当前种群P的区间最小和最大值,用式(6)求出反向个体,然后从集合{P,OP}选择Np个最优个体作为当前代种群P。
opi,j=MINpj+MAXp
j-pi,j(6)
步骤4 判断是否达到迭代终止条件,否则转向步骤2。
3 基于M-H采样的反向微分进化算法
3.1 M-H采样方法
3.1.1 马尔可夫链基本思想
M-H算法是出现较早一般化的马尔可夫链蒙特卡洛[11-12]采样方法,下面先介绍马尔可夫链(Markov Chain)。
定义3(马尔可夫链) 假定随机序列{X0,X1,…}满足马尔可夫性,即在任意时刻t≥0时,序列中某时刻t+1的状态Xt+1由条件分布p(Xt+1|Xt)产生,它只依赖时刻t的状态,与之前的状态{X0,X1,…,Xt-1}无关,这样的一个随机序列被称为马尔可夫链,马尔可夫链的转移核表示如下:
p(x,x′)=p(x→x′)=p(xt+1=x′|xt=x) (7)
定义4(马尔可夫链可逆) 若π(dx)P(x,dy)= π(dy)p(y,dx),x,y∈X则状态空间X上的马尔可夫链关于π(·)可逆。
定义5(平稳分布) 设πj(t)=π{X(t)=j},j∈X,如果关于π(x)可逆的马尔可夫链{X(t),t≥0}满足: πj=lim
t→∞πj(t),j∈X,则称π(x)为该马尔可夫链的平稳分布,平稳分布马尔科夫链的状态转移与初始值状态无关,只与时间间隔有关。
3.1.2 M-H采样思想
MCMC[13-14]基本原理是建立一个平稳分布,采样得到的马尔可夫链样本是一个π(x)样本,其基本步骤可概括为:
(1)构造马尔可夫链,在空间X的样本上选择一个合适的马尔可夫链,转移核设为p(*,*),使其收敛到平稳分布π(x)。
(2)样本提取过程:由空间X的某一点出发X0,用步骤(1)构造的马尔可夫链进行抽样模拟,产生序列X1,X2,…,Xn。
(3)蒙特卡洛积分:对任意整数m和任意足够大的整数n,任一个目标函数的f(x)期望估计为: f(x(t)) (8)
M-H方法最早由Metropolis等人提出,之后由Hastings加以推广,形成Metropolis-Hastings方法。
原理如下:假设马尔可夫链第t个时刻的状态为xt,π(x)是求解问题的目标分布,W(x,xt)是对称的转移函数。Metropolis-Hasting算法通过以下2步得到t+1时刻的状态:
(1)从转移分布W(x,x′)中得到x′,这里W(x, x′)是对称的概率转移函数,即W(x,x′)=W(x′,x)。
(2)取随机数U,使U服从(0,1)均匀随机分布,令r=min(1,π(x′)W(x′,x) π(x)W(x,x′) E[f(x)]= 1 n-m
n
t=m+1
∑
),如果U≤r,则令xt+1=x′;否则令xt+1=x。
3.2 M-HODE算法描述
微分进化算法中最核心的操作是变异操作,MHODE算法提出一种,将Metropolis-Hastings采样方法用于ODE的变异操作,M-HODE在初始化种群后求反向种群,合并初始种群和反向种群并计算每个种群的适应度值,根据适应度值大小进行升序排列,选取前NP个个体作为初始种群。在变异操作中用M-H采样方法选择基向量和差分向量,采样个体组成的马尔可夫链满足马尔可夫平稳分布。在进行变异,交叉,选择操作后,随机的进行反向种群更新,保持了种群的多样性,利于 M-HODE算法的全部优化。
3.3 M-HODE算法步骤
M-HODE算法步骤具体如下:
步骤1 随机产生均匀分布的种群P0,种群大小为NP,用式(5)计算得到种群个体的反向个体opoi,j=aj+bj-poi,j。从集合 P0,OP0),则可得r=min(1, π(x′) π(x) { }中选NP个个体作为初始种群。
步骤2 将种群里所有个体的按适应度值进行升序排列,计算排列后每一个个体的等级 Ri,公式为:
Ri=Np-i,i=1,2,…,Np (9)
步骤3 对每个向量个体进行等级分配后,计算每个个体的选择概率,这里用到已提出的平方模型式(10)[15],向量xi的选择概率计算公式为:
pi= RiNp ,i=1,2,…,Np (10)
步骤4 使用Metropolis-Hastings算法进行抽样参加变异操作的个体。以DE/rand/1策略作为实例,选取xr0,xr1,xr2,xr3为马尔可夫链。
M-H采样方法具体如下:
(1)当rand(0,1)>pr0且r0≠i条件满足时,随机选择r0∈{1,Np}。/*xr0作为马尔可夫链的初始
■■
2
■■向量*/
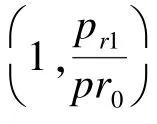
(3)如果U≤r,则x1=xr1,否则x1=xr0。/*选取x1为基向量*/
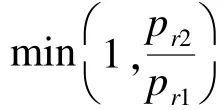
(5)如果U≤r,则x2=xr2,否则x2=xr1并且x1=xr2。/*x2作为差分向量*/
(6)r3≠r1、r3≠r0和r3≠i条件满足时随机选取r3∈{1,NP}。/*随机选取x3*/
步骤5 当函数评价次数小于最大评价次数以及迭代次数小于最大迭代次数2个条件满足时,进行差分进化算法的变异、交叉、选择操作得到种群P。
步骤6 随机反向代跳操作:如果跳转概率Jr大于(0,1)间的一个随机数,那么根据式(6)求出种群P的反向种群OP,然后从集合{P,OP}中选择NP个个体作为当前代种群P。
步骤7 重复迭代到算法停止迭代的条件为止。
4 仿真实验与结果分析
为测试M-HODE算法的有效性和正确性,这里用11个常用的标准测试函数进行仿真评价,将MHODE,DE,JDE及ODE算法进行比较。这11个测试函数中既有高维单峰也有高维多峰函数。其中,f4,f5,f73个函数是特殊维数,分别是10维、2维、2维,其他函数均是30维,另外,f6是一个噪声函数。测试函数的部分参数设置如表1所示。f5的最优值fmin=-1,其他函数的最优值fmin都为0。
本文实验仿真环境为Matlab2012,运行于Intel (R)Pentium(R)4,CPU 2.93 GHz,1 GB内存的联想台式电脑。仿真时设置最大迭代次数MAXIter= 1 000,函数适应度最大评价次数Max_NFFES= 10 000×D,缩放因子和交叉概率初始值分别设置为F=0.5和CR=0.8,反向操作的跳转概率Jr按照ODE算法的Jr取一样值。为验证该算法的精确性,将每个算法独立运行50次,取50次实验结果的平均值和标准方差作为评价算法的主要性能指标,为验证算法的快速收敛,在实验条件的基础上加上目标值VTR=1.0E-10的条件,计算50次所用平均时间。
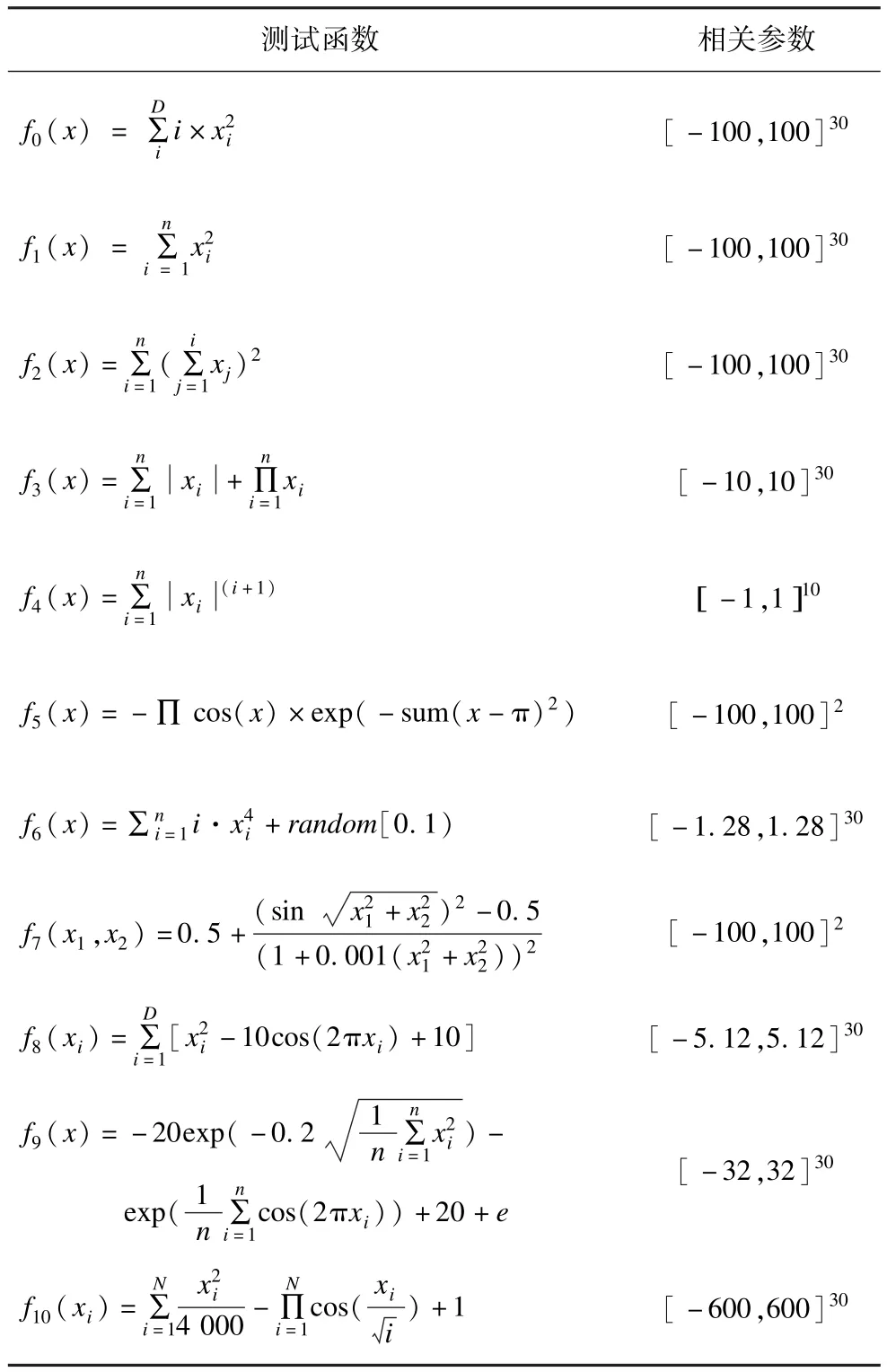
表1 测试函数及相关参数
表2是DE,JDE,ODE及M-HODE算法的实验结果,加粗数据表示最优值。统计表2中的测试函数数据,f0~f4这5个高维单峰函数中有4个函数M-HODE均值优于DE,JDE,ODE算法;2维函数f5的实验结果都是一样的,针对噪声函数f6,M-HODE方差比其他3个算法方差更小,说明M-HODE具有更好的抗噪性;多峰函数f7~f10中有3个函数 MHODE均值优于DE,JDE,ODE算法,M-HODE方差比其他3个算法较小,该优越性归功于M-HODE算法中M-H采样的平稳性。可见,针对一些高维多峰函数优化,M-HODE具有明显优势。
图2~图4给出了f1,f2和f103个具有典型高维测试函数的迭代曲线,迭代次数为1 000次,按一定比例用线条标出,从图2~图4可以看出,M-HODE算法、DE算法、JDE算法、ODE算法曲线趋势相似,但是M-HODE算法有更快的收敛速度和更优的精度。图4对于f10函数,M-HODE算法表现出更加明显的收敛速度和收敛精度。这归功于M-HODE采样方法的稳定性和反向进化的种群多样性,促进了算法的快速收敛。针对其余的测试函数,实验也获得了相似的进化曲线。
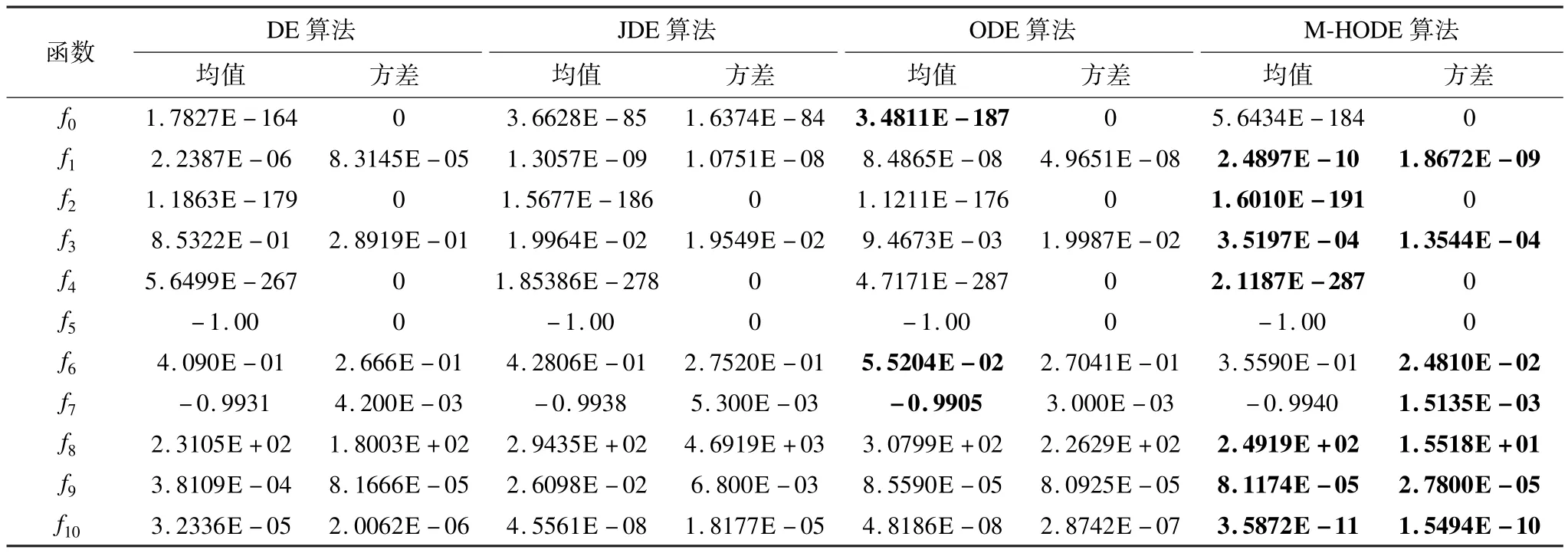
表2 DE,JDE,ODE,M-HODE算法均值和方差
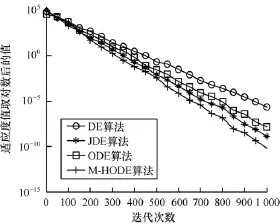
图2 f1函数迭代曲线
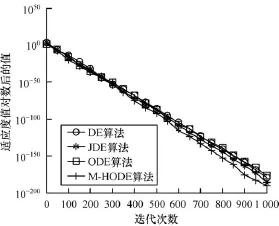
图3 f2函数迭代曲线

图4f10函数迭代曲线
图5是DE,JDE,ODE和M-HODE算法运行时间比较,仿真设置为VTR=1.0E-10,最大迭代次数MaxIter=1 000,函数适应度最大评价次数Max_NFFES=10 000D。从图5可以看出,在运行时间上M-HODE优于DE,JDE,ODE这3个算法,针对有些函数M-HODE算法所用迭代时间甚至可以快到上百倍。M-H采样很大程度上不仅可以提高差微分进化函数的优化精度,而且可以加快函数优化的收敛速度,使优化很快趋于平稳,并减少时间复杂度。
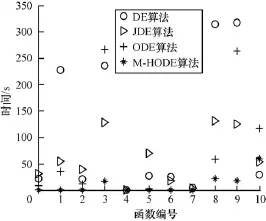
图5 算法运行时间比较
5 结束语
本文提出一种基于M-H采样的快速反向微分进化算法,将M-H采样策略用于反向微分进化算法中,M-H采样个体组成平稳分布的马尔可夫链,能改进ODE算法的变异操作。通过对11个典型的Benchmark函数进行测试,结果表明,M-HODE算法不仅在高维单峰函数和高维多峰函数优化中具有较高的精度,而且M-H采样能加快M-HODE算法的收敛速度,避免陷入局部最优,从而实现M-H快速反向微分进化算法。
[1] Storn R,Price K.Differential Evolution——A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces[R].Berkley,USA:ICSI,Technical Report:TR-95-012,1995.
[2] Storn R,Price K.Differential Evolution——A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization,1997,11(4): 341-359.
[3] Mallipeddi R,Suganthan P N,Pan Q K,etal.Differential Evolution Algorithm With Ensembleof Parameters and Mutate on Strategies[J].Applied Soft Computing,2011,11(2):1679-1696.
[4] Brest J,Greiner S,Boskovic B,et al.Self-adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems[J].IEEE Transactions on Evolutionary Computation, 2006,10(6):646-657.
[5] Brest J,Maucec M S.Self-adaptive Differential Evolution Algorithm Using Population Size Reduction and Three Stragies[J].Soft Computing,2011,15(11):2157-2174.
[6] Gong Wenyin,Cai Zhihua.Differential Evolution with Ranking-based Mutation Operators[J].IEEE Transactions on Evolutionary Computation,2013,43(6):1-16.
[7] 张雪霞,陈维荣,戴朝华.带局部搜索的动态多群体自适应差分进化算法及函数优化[J].电子学报,2010, 38(8):1825-1830.
[8] 王筱珍,李 鹏,俞国燕.分阶段二次变异的多目标混沌差分进化算法[J].控制与决策,2011,26(3):457-463.
[9] Qu B Y,Suganthan P N,Liang J J.Differential Evolution with Neighborhood Mutation for Multimodal Optimization[J].IEEE Transactions on Evolutionary Computation,2012,16(5):601-614.
[10] Rahnamayan S,Tizhoosh H R,Salama M M A.Oppositionbased Differential Evolution[J].IEEE Transactions on Evolutionary Computation,2008,12(1):64-79.
[11] Karandikar R L.On the Markov Chain Monte Carlo (MCMC)Method[J].Sadhana,2006,31(2):81-104.
[12] Gallagher K,Charvin K,Nielsen S,et al.Markov Chain Monte Carlo(MCMC)Sampling Methods to Determine Optimal Models,Model Resolution and Model Choice for Earth Science Problems[J].Marine and Petroleum Geology,2009,26(4):525-535.
[13] Chen Peide.Hasting-metropolis Algorithms and Reference Measures[J].Elsevier Statistics&Probability Letters,1998, 38(4):323-328.
[14] Eidsvik J,Tjelmeland H.On Directional Metropolis——Hastings Algorithms[J].Statistics and Computing, 2006,16(1):93-106.
[15] Kalelo P,Ali M M.Differential Evolution Algorithm Using Hybrid Mutation[J].Computational Optimization and Application,2007,37(2):231-246.
编辑 陆燕菲
Fast Opposition Differential Evolution Algorithm Based on M-H Sampling
TU Weiwei,GE Hongwei,YANG Jinlong,YUAN Yunhao
(School of IOT Engineering,Jiangnan University,Wuxi 214211,China)
In Differential Evolution(DE)algorithm,the population initialization is updated by using opposition optimization rule,so as to maintain the population diversity.However,the reverse individuals are easy to deviate from the global optimal solution,has slow convergence speed and easy to fall into local optimum in function optimization.This paper proposes a fast Opposition Differential Evolution(ODE)algorithm based on M-H(Metropolis-Hastings)sampling method.M-H sampling is used in the mutation operation of ODE.M-H sampling satisfies Markov Chain reversible conditions.One step transition probability of Markov Chain is calculated according to the selecting probability of individual ranking-assignment,not only chooses the best individual,but also searches for the optimal direction and keeps the population diversity.Simulation results show these individuals from M-H sampling have Markov stationary distribution property.The algorithm can accelerate the speed of convergence in unimodal functions and multimodal functions,balance the performance of global searching and local searching,and has higher precision and better robustness.
Differential Evolution(DE)algorithm;Opposition Differential Evolution(ODE)algorithm;transition probability;stationary distribution;Markov Chain Monte Carlo(MCMC);Opposition-based Learning(OBL)
1000-3428(2014)11-0155-05
A
TP301.6
10.3969/j.issn.1000-3428.2014.11.031
国家自然科学基金资助项目(61305017);江苏省自然科学基金资助项目(BK20130154);江苏高校优势学科建设工程基金资助项目。
涂维维(1987-),女,硕士研究生,主研方向:微分进化,人工智能,模式识别;葛洪伟,教授、博士;杨金龙、袁运浩,副教授、博士。
2013-12-13
2014-01-13E-mail:tuweiweier@163.com
中文引用格式:涂维维,葛洪伟,杨金龙,等.基于M-H采样的快速反向微分进化算法[J].计算机工程,2014,40(11): 155-159.
英文引用格式:Tu Weiwei,Ge Hongwei,Yang Jinlong,et al.Fast Opposition Differential Evolution Algorithm Based on M-H Sampling[J].Computer Engineering,2014,40(11):155-159.
