二维主元分析法在心肌梗死心电信号检测中的应用

葛丁飞， 徐爱群

（1.浙江科技学院信息与电子工程学院，浙江杭州 310012；2.浙江科技学院机械与汽车工程学院，浙江杭州 310012）

二维主元分析法在心肌梗死心电信号检测中的应用

葛丁飞1， 徐爱群2

（1.浙江科技学院信息与电子工程学院，浙江杭州 310012；2.浙江科技学院机械与汽车工程学院，浙江杭州 310012）

利用基于联合能量百分比搜索的二维主元分析法对12导高分辨率心电信号（ECG）进行全局特征提取和分类检测研究。所用数据取自PTB诊断数据库，包括健康状态ECG，早期心肌梗死（MI）ECG，急性期MIECG，恢复期MIECG。结果表明，所用的方法能有效地融合12导ECG信号及其高频分量中的细微结构信息，与常规主元分析法相比，其平均分类检测精度可提高10.43%，与常规二维主元分析法相比，能得到维数更低的特征表示，并可获得99.46%的平均分类检测精度。

计量学；心电信号；主元分析；心肌梗死；特征提取

1 引 言

早期心肌梗死（Myocardial Infarction in Early Stage，MIES）的及时发现对降低冠心病患者死亡率起着至关重要的作用。判断病程处于何种阶段，ECG信号（Electrocardiogram，ECG）的特征提取是关键。现有的计算机辅助诊断系统大多是依据ECG特征参数进行决策判断的，然而，ECG特征参数只能反映疾病的局部特征，不能反映其全局特征［1，2］。研究表明，当冠心病患者出现胸痛症状并继发心肌梗死（Myocardial Infarction，MI）时，有时难以从常规的12导ECG中观测到特征参数的明显或高水平的改变［3，4］，并且在MI演变过程中反映在ECG上只体现在局部细节上的差异，这给MIECG特征提取与检测带来了严峻挑战。

本研究尝试从12导高分辨率ECG（High Resolution ECG，HR-ECG）中提取全局特征研究，这也是鉴于以下事实：HR-ECG采样频率可高达1 000 Hz，包含了更丰富的高频分量，而高频ECG信号（100 Hz以上的频率分量）在时域上存在比ECG特征参数改变还要敏感的诊断信息［5］，利用HR-ECG能更有效地提取ECG全局特征；12导联ECG比单导联ECG能更全面地反映疾病的全貌。12导HR-ECG的使用需要克服高维特征矢量降维困难的问题，利用线性判别分析法不仅只能提取有限数量的特征，而且还会遇到小样本问题［6］。就主元分析法（Principal Component Analysis，PCA）而言，尽管通过矩阵的奇异分解可避开高维协方差矩阵计算困难，但这并不意味着特征投影矢量计算精确性问题的解决，因为PCA技术是依赖于传统统计特性的，要求有足够的训练样本［7］。在MI ECG信号特征提取的研究中发现：假使不存在小样本问题，该方法依然不能始终保证类内散度矩阵的非奇异性。将12导HR-ECG信号以二维矩阵的形式加以表示，并利用二维主元分析法（Two-dimensional PCA，2DPCA）进行信息融合并提取特征，其中利用一种基于联合能量百分比（Energy Percentage，EP）搜索的特征值及本征向量选择方法，使特征维数大幅下降，分类检测精度得以提高，并更具广义性。实验结果表明，基于联合EP搜索法的2DPCA技术可从HF-ECG中提取的最少有效特征仅为36个，并可取得99.46%的平均分类精度。

2 方 法

2.1 ECG信号的预处理

表1为取自德国PTB诊断数据库ECG数据，不同阶段MIECG包括：健康状态（Health Control，HC）ECG、MIES ECG、急性期MI（MI in Acute Stage，MIAS）ECG和恢复期MI（MI in Recover Stage，MIRS）ECG。数据采样频率为1 000 Hz，其原始数据频带宽为0～500 Hz。利用一个50 Hz陷滤波器来消除电源噪音，一个截止频率为0.05 Hz高通滤波器消除基线漂移。图1为一个典型的常规导联ECG波形。由MIECG图形演变过程看，各阶段的MI有其自身的特点：MIES：ST段开始升高，异常性Q波尚未出现；AMI：ST段升高后开始下降，并出现异常性Q波；MIRS：ST段恢复正常，异常性Q波依然存在。文中利用Tompkin算法来检测ECG信号的峰值［8］。一般地，P波位于ECG峰值R前0.12～0.2 s内，T波位于ECG峰值R后0.16～0.32 s内，因此文中以0.9 s窗口（0.3 s位于峰值R前，0.6 s位于R后）对ECG信号进行分割是合理的。

表1 取自PTB诊断数据库的实验数据

图1 一个典型常规心电导联ECG波形

2.2 ECG信号的矩阵表示

每个ECG样本进行信号分割后组成12个ECG导联序列。为了融合12导ECG信息，本文采用矩阵表示12个ECG序列，称为ECG样本矩阵M，其中的每一列由各导联某一时刻采样值组成，反映了不同导联间的相关性，每一行依次由ECG导联I，II，III，aVR，aVL，aVF，V1，V2，V3，V4，V5，V6组成，反映了同一心动周期内相关性。

2.3 基于2DPCA的ECG特征矩阵的提取

2.3.1 ECG矩阵行方向上的特征提取

将2DPCA应用于上述矩阵M的特征提取过程称为ECG矩阵行方向（或信号方向）上的特征提取。2DPCA寻找一组特征投影矢量X使样本矩阵经Y＝MX投影后特征矩阵总体散度最大［7］：

式中，Sx为样本矩阵M投影后的协方差矩阵；tr（）为轨运算。假设Gt为ECG样本矩阵M的协方差，则有J（X）可表示为使J（X）最大化的特征投影矢量X为Gt最大特征值所对应的本征向量，式（2）可按下式计算

式中，N为ECG样本矩阵的个数；Mj为第j个ECG样本矩阵为N个ECG样本矩阵均值。选取前d1个最大特征值所对应的本征向量组成特征投影矢量矩阵X＝［X1，X2，….，Xd1］。特征矩阵MX主要反映了同一心动周期内的融合信息。

2.3.2 ECG矩阵列方向上的特征提取

将2.2节中所述的ECG样本矩阵M进行转置得到MT，将2DPCA应用于MT提取ECG特征的过程称为ECG矩阵列（或导联）方向上的特征提取。按2.3.1节中的方法可以得到特征投影矢量矩阵Z＝［Z1，Z2，…，Zd2］，d2为所选最大特征值的个数，ZTM主要反映了ECG各导联间的融合信息。

2.3.3 ECG矩阵行与列方向上的特征提取

为了进一步融合ECG各导联和同一心动周期内的有效信息，对ECG矩阵M做如下变换

式中，C为一个d2×d1特征矩阵，C矩阵中的每一元素即为所提ECG特征。

2.4 特征投影矢量选取

2.4.1 基于独立EP准则的特征投影矢量选取

最流行的特征投影矢量（本征向量）选择方法为选取前L个最大特征值，使样本在所选特征值对应的投影轴上的能量占整个能量的99%以上［9］，即能量百分比准则。如果基于该准则得到上述行和列方向上最大特征值个数分别为d2＝L2和d1＝L1，那么特征矩阵C为一个L2×L1的矩阵。由于以上的特征矢量选择过程是在行和列方向上独立进行的，所以本文称为独立EP准则。

2.4.2 基于联合EP搜索法的特征投影矢量选取

研究表明，上述方法所提取的特征数量依然过多，提出联合EP搜索法，以减少所提特征数量。

（1）EP矩阵构造及敏感性函数值计算

用E表示联合EP矩阵，其维数与特征矩阵C相同，其中的第i行第j列元素为Rij（称为能量点）。将独立EP准则所选最大特征值分别在行和列方向上从大到小依次排列，并分别计算各特征值在各自方向上所占百分比，在行（或列）方向上计算出特征值百分比累加上i（j）的值，再进行行和列方向上加权平均即可得到Rij，加权系数与L1，L2成正比，其计算式为

式中，rm为在行方向上的第m个特征值；rn为在列方向上的第n个特征值。

为了衡量被选特征值数量变化对EP变化的影响，计算敏感性函数Sij，其方法为：在搜索点转移时，能量点EP的增量变化率除以被选最大特征矢量数量增量变化率。当搜索点从（i，j－1）转移到（i，j）时，如果在某列J之后，Sij显著减小，则在行方向上可将EP矩阵划分为：列号大于J的为不敏感区，列号小于J的为敏感区，列号等于J的为敏感性边界区。类似地，当搜索点从（i－1，j）转移到（i，j）时，在列方向上同样可将EP矩阵划分为与上述相应的3个区。

（2）EP矩阵搜索区划分和搜索种子点的选择

在矩阵EP中，将Rij小于某一待定常数α的能量点划分为非搜索区，将Rij≥α的能量点划分为搜索区和边界区，将其与非搜索区相邻的能量点划分为搜索边界区。在搜索边界区中，对应于行数和列数乘积最小的能量点为搜索种子点。

（3）搜索的方法

图2给出了详尽搜索方法，搜索将在搜索区及其边界区内从左（上）到右（下）进行。在搜索过程中，如果某点不在敏感区上，需要进行相应的分类测试，并检查是否满足分类精度要求。如果某点在敏感区上，则从该点开始在相应方向上按如下优先权向最近邻点转移：（1）EP较大的点；（2）行数与列数乘积较小点。

2.5 ECG特征的分类

本文采用二叉树对ECG特征进行分类，其中的每一步只是一个两类分类问题。为了构造这一决策树，以类间欧氏中心距为类间可分性准则进行分组，其特点为：在同一组中的类间中心距相对较小，而不同组间的类间中心距相对较大。在每一步分类中，进行了基于线性分类器的分类，并依据阈值零进行决策分类，即当判别函数值＞0时，将样本决策为一类；当判别函数值＜0时，将样本决策为另一类［10］。

图2 搜索方法

3 结 果

3.1 基于独立EP准则的2DPCA特征提取和分类结果

依据独立EP准则，在行方向和列方向上所选本征矢量的个数分别为L1＝23和L2＝7。ECG样本在投影轴上的能量占整个能量99%的条件下，d1＝L1＝23，d2＝L2＝7。特征投影矩阵X和Z分别为1个900×23和1个12×7的矩阵。依据式（5）可得到1个7×23的特征矩阵C。因此，1个ECG样本可用161（＝7×23）个特征来表示。

计算HC、MIES、MIAS和MIRS之间的欧氏中心距表明，MIES、MIAS和MIRS之间分布相对紧密，而HC和MIES／MIAS／MIRS之间相对离得较远，所以在分类的第一步，HC从MIES／MIAS／MIRS中首先被分离开来。类似地，在分类的第二步，MIRS从MIES／MIAS中被分离开来，最后将MIES和AMI进行分离。表1中训练的样本是从总样本集中随机选取的，其20次分类测试的结果为：HC（100%），MIES（98.94%），MIAS（99.49%），MIRS（99.77%）。

3.2 基于联合EP搜索法的2DPCA特征提取和分类结果

由上可知，ECG样本依据独立EP准则在行方向和列方向上所选最大特征值个数为23和7。因此，能量矩阵E为1个7×23矩阵。依式（6）计算出矩阵元素Rij值，其部分元素值见表2。实验结果表明，在行方向上进行搜索时，当列号大于12后，Sij值显著减小，行方向所选特征矢量个数的增加对EP增加的影响显著减小，将表2中列号等于12，大于12和小于12的区域分别定义为行方向上EP敏感性边界区、EP不敏感区和EP敏感区。基于同样的理由，定义表2中行号等于3，大于3和小于3的区域分别为列方向上EP敏感性边界区、EP不敏感区和EP敏感区。

表2 E矩阵部分元素值

常数α的选择直接影响EP矩阵搜索区及其边界的划分，进而影响种子点的选择和最终能量点的确定。为此，本文选用多个α值进行实验研究。当α＝0.9时，表2中黑体加粗部分为搜索边界区，其左边和上方为非搜索区，其下方为搜索区。能量点（3，8）和（2，12）同时被选为种子点，其搜索结果及其分类精度见表3。

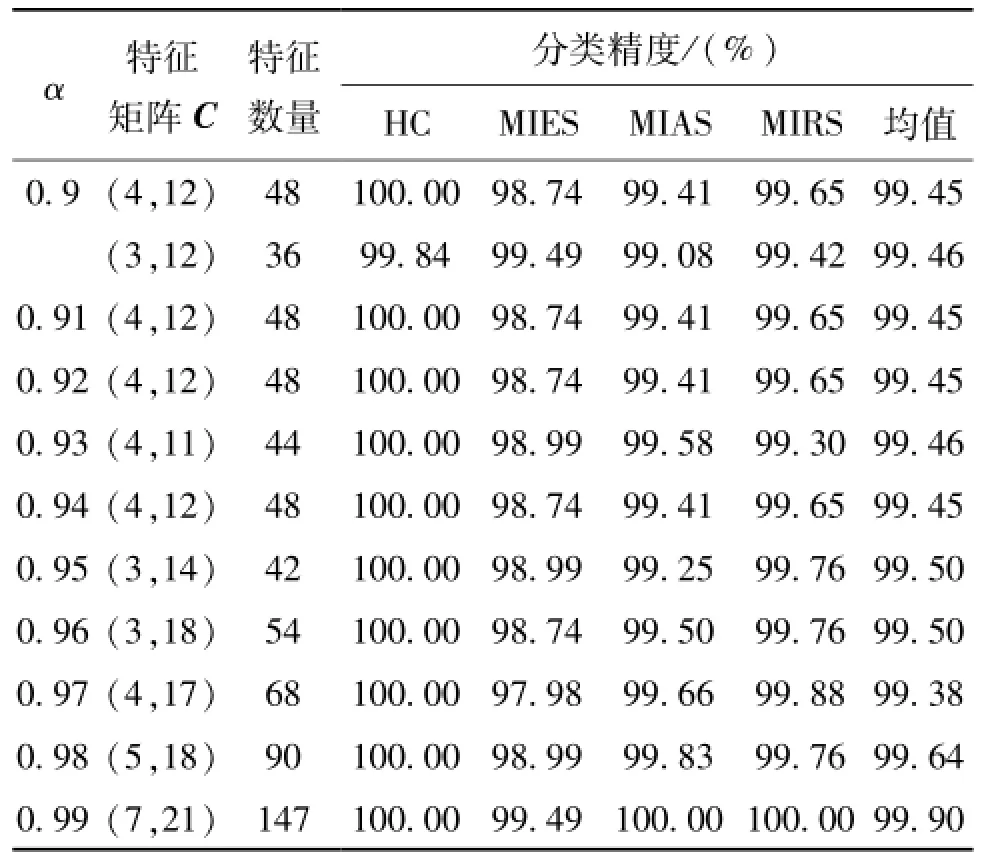
表3 联合EP在不同α下所提特征数量及分类精度

当选（3，8）为种子点时，以均值99%为预期分类效果，其搜索过程为：由于能量点（3，8）位于列方向EP敏感性边界区上，取d1为8，d2为3，进行2.5节中所述的分类测试，其平均分类精度为93.51%，未能达到预期分类效果。点（3，8）在行方向和列方向上的最近邻点为（3，9）和（4，8），其EP值均为0.918，按沿对应点行数和列数乘积较小的方向搜索规则，将搜索点在行方向从（3，8）转移至（3，9）。由于点（3，9）位于行方向上的EP敏感区内，无须进行分类测试。（3，9）的最近邻点（3，10）和（4，9），其EP值分别为0.929和0.930，按沿EP较大的最近邻点搜索规则，将搜索点在列方向从（3，9）转移至（4，9）。点（4，9）位于列方向的EP不敏感区内，对点（4，9）进行分类测试，得到分类精度均值为97.04%，依然未能达到预期分类效果。再依此将搜索点转移至（4，10）、（4，11）、（4，12）。点（4，12）位于行方向上的EP敏感性边界区，对该点进行分类测试，得到平均精度为99.45%，符合预期效果，所以（4，12）被选为当α＝0.9和种子点为（3，8）时搜索终止点，其对应特征维数为48。类似地，当α＝0.9和种子点为（2，12）时可得到搜索终止点为（3，12），其对应的特征维数为36。

表3还给出了当α取0.9～0.99其它值时的搜索结果及其分类精度。由表3可见，当α取0.9～0.99时，所提特征最小个数为36，并取得了均值99.46%的分类精度。

为了比较研究，本研究利用与上述相同的ECG数据进行基于传统PCA＋独立EP准则特征提取和分类研究，其结果见表4。在该研究中，得到所提特征数量为145，应用LDA法进行再次特征提取并分类，即PCA＋独立EP＋LDA，得到平均分类精度分别为86.52%。有关实验条件为：（1）采用相同的信号滤波技术和分割方法；（2）采用将12导ECG信号串接成一维特征矢量的常规做法；（3）为了克服传统PCA技术面对的超高维协方差矩阵计算困难，将ECG信号频率降低至125Hz。利用LDA法对2DPCA＋独立EP法得到的161个特征进行进一步特征提取并分类，得到平均分类精度为95.29%。

表4 基于2D-LDA和PCA特征提取与分类精度比较

4 讨 论

本文主要目的是利用2DPCA分析技术从12导HF-ECG中提取全局心电特征，更好地对MI实现阶段性分类检测。如果采用常规的将12导HR-ECG信号串接成一维ECG特征矢量的方法，那么将形成一个10800维的原始向量空间，相关的协方差矩阵为10800×10800的超大矩阵，这给问题的后续处理带来了极大的困难。文中的2DPCA方法实际上是将高维向量空间中特征提取的过程分解为低维向量空间中多步来完成，并且2DPCA样本协方差矩阵可直接利用ECG样本矩阵进行计算，这使问题的处理变得简单可行。相比于传统PCA，2DPCA协方差矩阵维数要低得多。就本研究而言，在行方向和列方向上的协方差矩阵分别为一个900×900和12×12的矩阵。所以文中的方法为12导HF-ECG的特征提取提供了一个可行的技术方案。

独立EP准则是常规PCA分析技术中最流行的特征投影矢量选择方法。由表4可见，2DPCA＋独立EP准则的方法可提取161个MIECG特征，并可取得均值为99.30%的分类精度，该方法之所以能取得令人满意的分类结果是因为保持了ECG高频分量中的许多丰富的诊断信息。利用PCA＋独立EP方法可提取145个特征，其平均分类精度为89.03%，这不是一个令人满意的结果，主要是因为虽然125 Hz ECG信号满足了临床诊断上带宽应保持在0～100 Hz的要求，但丢失了HR-ECG高频分量中许多丰富的诊断信息，这进一步说明了在MI阶段性分类检测中使用HR-ECG的必要性。

2DPCA＋独立EP准则的方法虽然可取得令人满意的分类效果，但所提取的特征数量依然高达161。实际上，现有的2DPCA的相关应用研究都是基于独立EP准则的。表3可见，将联合EP搜索法应用于2DPCA中特征值及其特征投影矢量的选择，可获得最少的特征数量仅为36，其分类精度均值为99.46%。相比于独立EP准则，联合EP搜索法应用于2DPCA的特征提取可剔除更多冗余数据，并可取得同样令人满意的分类效果。

联合EP矩阵搜索区域划分不仅使种子点的选择变得简单化，而且使搜索速度得以加快。由表3看到，提取特征数量随α的增大呈现总体增加趋势。当α＝0.9时，终止点（3，12）恰好是最优的搜索结果。当α＝0.99时，基于终止点（7，21）的分类虽能获得满意的分类效果，但所提取的特征维数较高。研究表明，分类精度与EP变化规律相一致，较为合理的α选择是0.9～0.95，这能使搜索范围和收敛速度得到兼顾，能以较少数量的特征取得理想的分类效果。

由于2DPCA样本协方差矩阵直接利用ECG样本矩阵进行计算，而无需在12导ECG串接成一维特征矢量后进行，因此相比于传统PCA，2DPCA协方差矩阵维数要低得多，相对同样的样本数量而言，2DPCA获得特征投影矢量更加精确，并更具广义性，同时也节约了大量的计算资源。

5 结 论

基于联合EP搜索法的2DPCA技术应用于12导HR-ECG的特征提取以实现MI阶段性分类检测是可行的。文中的方法不仅能有效地融合12导ECG信息，而且能有效地提取隐含在HR-ECG敏感细微结构中的诊断信息；不仅比常规PCA获得更高的分类精度，而且能获得比2DPCA＋独立EP准则维数更低、分类效果同样令人满意的心电特征矢量。

［1］ Dhruva N V，Abdelhadi S I，Anis A，et al.ST-segment analysis using wireless technology in actue myocardial infarction（STAT-Trial）［J］.Journal of the American College of Cardiology，2007，50（6）：509－13.

［2］ Huang C S.A vector cardiogram-based classification system for the detection of myocardial infarction［C］／／Proceeding in 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society，Boston，2011.

［3］ Joo T H，Schm itt PW，Hampton D R，et al.Enhanced acutemyocardial infarction detection algorithm using local and global signal morphology［C］／／Computer in Cardiology，Cleveland，OH，1998.

［4］ Edenbrandt H L，Ohllsson M.Detecting acutemyocardial infarction in 12-lead ECG using Herm ite expansions［J］.Artificial Intelligence in Medicine，2004，32（2）：127－136.

［5］ Abboud S，Zlochiver S.High-frequency QRS electrocardiogram for diagnosing and monitoring ischemic heart disease［J］.Journal of Electrocardiology，2006，39（1）：82－86.

［6］ Mohamed H J，Noureddine Z.Face recognition system using relevance weighted two dimensional linear discriminant analysis algorithm［J］.Journal of Signal and Information Processing，2012，3（1）：130－135.

［7］ Yang J，Zhang D，Frang A F，etal.Two-dimensional PCA：a new approach to appearance-based face representation and recognition［J］.IEEE Transaction Pattern Analysis and Machine Intelligence，2004，26（1）：131－137.

［8］ Tompkins W J.Biomedical Digital Signal Processing［M］.Englewood Cliffs，New Jersey：Prentice Hall，1993.

［9］ Anderson C W，Stolz E A，Shamssunder S.Multivariate autoregressive models for classification of spontaneous electroencephalographic signals duringmental tasks［J］.IEEE Trans Biomed Eng，1998，45（3）：277－286.

［10］ 葛丁飞，孙丽慧，文小军.基于Frank导联和Hermite展开的心肌梗死检测［J］.计量学报，2009，30（6）：551－554.

The Application of Two Dimensional Principal Component Analysis in the Detection of Myocardial Infarction ECG Signals

GE Ding-fei1， XU Ai-qun2
（1.School of Information and Electronic Engineering，Zhejiang University of Science and Technology，Hangzhou，Zhejiang 310012，China；2.School of Mechanical and Automotive Engineering，Zhejiang University of Science and Technology，Hangzhou，Zhejiang 310012，China）

The joint energy percentage（EP）search method based on two dimensional principal component analysis is introduced to extract global features from 12-lead high resolution electrocardiogram（ECG）for the purpose of classification. Four types of classes are collected from PTB clinical diagnostic database，which corresponding patient's statuses are health control，myocardial infarction（MI）in early stage，MI in acute stage and MI in recover stage，respectively.The experimental results show that the information can be fused efficiently using the proposed method，which are from 12-lead ECG and the details contained in high frequency components of ECG.The average classification accuracy can be increased by 10.43%compared with that of conventional principal component analysis.The ECG signal can be represented with lower dimensions compared with that of independent EP criterion，and an average classification accuracy of99.46%can be achieved.

Metrology；ECG signal；Principal component analysis；Myocardial infarction；Feature extraction

TB97

A

1000-1158（2014）03-0252-06

10．3969／j．issn．1000-1158．2014．03．12

2012-07-18；

2013-05-26

国家自然科学基金（61074143）；浙江省自然科学基金（Y1100219）；浙江科技学院学科交叉预研专项重点项目（2012JC01Z）

葛丁飞（1965－），浙江东阳人，浙江科技学院副教授，研究方向为模式信息处理以及生物医学信号检测与处理。gedingfei＠163.com