低信噪比下基于Chirp信号的频率特性测试方法

魏列江， 李旭方， 王 霖， 董万玉， 孟 犁

（1.兰州理工大学能源与动力工程学院，甘肃兰州 730050； 2.甘肃省计量研究院，甘肃兰州 730060）

低信噪比下基于Chirp信号的频率特性测试方法

魏列江1， 李旭方1， 王 霖1， 董万玉1， 孟 犁2

（1.兰州理工大学能源与动力工程学院，甘肃兰州 730050； 2.甘肃省计量研究院，甘肃兰州 730060）

提出采用带通滤波和小波包变换对响应信号进行预处理，再由FFT分析和处理获得系统频率特性曲线的方法，较好地解决了低信噪比下的系统频率特性测试问题，并降低了测试时对采集系统的硬件要求。实验结果表明：对于截止频率以下的频段，在信噪比较低甚至为－20 dB时，可以得到精度不低于1 dB的幅频特性曲线和不低于3°的相频特性曲线，完全满足系统性能评价和控制器设计的应用要求。

计量学；频率特性；小波包变换；FFT

1 引 言

在控制系统性能评价和控制器设计过程中，频率特性是最为重要的系统特性之一。系统频率特性曲线测试通常采用FFT的分析方法获得，该方法以Chirp信号作为被辨识系统的激励信号，将输入与输出信号作FFT变换，并计算出每个频率处的响应信号与激励信号的幅值比、相位差，由这些计算结果就可以得到被测系统幅频特性和相频特性曲线［1］。这种方法具有计算效率高、测试速度快的特点［2］。但是这种方法在导弹和飞机等飞行器的发动机喷管摆角控制、飞机起落架收放、船舶的减摇鳍运动控制等系统的频率特性测试中往往不能获得可信的结果。因为这类系统广泛采用电液伺服阀控制的液压缸作为执行机构来推动负载运动，系统通常工作在平衡点附近很小的范围内，所以测试其频率特性时Chirp信号的幅值很小，在测试过程中系统的采样量化误差和测量通道干扰所带来的噪声很容易造成信噪比较低的情况，当信噪比低于10 dB以下时，直接对Chirp信号激励和系统响应数据进行FFT分析和处理，获得的系统频率特性曲线并不能满足控制系统性能评价和控制器设计的要求。

2 基于Chirp信号的频率特性测试原理

图1所示为基于Chirp信号的频率特性测试原理，以Chirp信号作为被测系统的激励信号，对激励信号x（t）和响应信号y（t）同时进行高速采集，得到x（k）和y（k）（k＝1，2，…，n；n为最大采样点数），然后采用FFT算法将时域输入输出数据变换到频域内，得到激励信号和响应信号的离散频谱X（jωk）和Y（jωk），则被测对象的频率特性为：

通过式（1）计算得到每个频率处的响应信号与激励信号的幅值比、相位差，由这些计算结果就可以获得被测系统幅频特性和相频特性曲线。

图1 基于Chirp信号的频率特性测试原理

3 测量噪声对频率特性曲线的影响

测量噪声包括采样量化和测量通道干扰所带来的噪声，这两种噪声叠加影响采样数据的信噪比。随着A／D位数的增加，量化误差对响应信号附加的畸变幅度减小，以舍入法处理尾数为例，对于定点舍入的情况，A／D位数每增加1 bit，信噪比增加约6 dB［3］。由于采样量化误差和测量通道的干扰均可视为白噪声序列，因此可以用白噪声模拟测量噪声。测量噪声很容易使得小幅值测量的采样数据信噪比低于10 dB，直接影响频率特性曲线的测试精度。并且，由于在系统工作的平衡点进行测量，系统具有一定的稳态直流分量，也会影响频率特性曲线的测试精度。在Matlab环境下，以典型二阶系统作为被测系统进行仿真研究，典型二阶系统的传递函数为：

令ξ＝0.2，ωn＝1，输入Chirp信号频率特性测试范围为0.001～20 Hz。在测量通道中信号y（k）加入白噪声作为测量噪声，使得信噪比为1 dB，在系统无稳态直流分量的条件下，对Chirp激励信号和响应数据进行FFT分析和处理，获得的被测系统频率特性曲线如图2所示。如果在y（k）中再加入5 V稳态直流分量，对Chirp信号激励和响应数据进行FFT分析和处理，获得的被测系统频率特性曲线如图3所示。对比分析图2和图3可知，系统在受到测量噪声干扰的情况下，会影响频率特性曲线的测试精度，而且当系统具有稳态直流分量时，会直接影响FFT的能量值，频率特性曲线的测试精度更低。

图2 SNR＝1，系统无稳态直流分量

图3 SNR＝1，系统有稳态直流分量

4 带通滤波

为消除平衡点稳态直流分量对系统频率特性曲线测试的影响，可采用高通滤波器消除稳态直流分量。为避免信号频谱混叠情况出现，可采用低通滤波器作为抗混叠滤波器，还可以滤掉高频干扰信号，综合考虑可采用带通滤波器来实现。

带通滤波器的带通下限截止频率ωl和带通上限截止频率ωh可分别由Chirp信号的起始频率f0和系统采样频率fs来确定，即：

式中，Kl和Kh取值与Chirp信号的起始频率、终止频率及被测系统的形式有关，可在对稳态直流分量的滤除速度和滤除效果进行折中后选取。经过在Matlab下对测量通道中具有白噪声的二阶系统中的直流分量进行滤波仿真分析，Kl取在0.01～0.1之间，Kh取在2～3之间，且fs≥2fn（fn为Chirp信号的终止频率）时，可以获得较满意的结果。

5 基于小波包变换的信号去噪

经过带通滤波之后的Chirp信号响应数据仍含有大量噪声，需尽可能地提取被噪声覆盖的真实Chirp信号响应数据。由于小波包变换具有时频局部化和多分辨率的特性，对小波分解中所得到的高频部分再继续细分为一些子频带，并对每个子频带提取各自的阈值，具有更精细的信号去噪能力［4］。在Chirp响应信号高频部分，有用信号被较好地保留下来。因此，本文采用小波包变换作为工具对经过带通滤波的Chirp响应信号数据进行更为精确的滤波。

对Chirp响应信号进行逐层7级小波包分解，以有效反映子频带的范数随分解层数的变化。如果某个子频带内的小波系数极大模值较大，且随着层数的增大而增大，表明信号的能量主要集中在该子频带内。为此，引入子频带范数：

依据最小熵原则［5］，在各层上寻找范数大于均值的子频带，并根据子频带一分为二的小波包分解特点，考察其范数随各层的变化，如果随层数的增大范数出现一最大峰值，则保留该最大峰值所对应的子频带，将范数小于均值和范数虽大于均值但随各层层数的增大范数不出现最大峰值的子频带内的小波系数视为零而舍去，根据最佳熵的原则设定下面的浮动阈值：式中，M为子频带内的小波系数个数，A为子频带范数。将幅值小于t的小波系数置零，保留大于t的小波系数，最后，由剩下的小波系数重构信号。

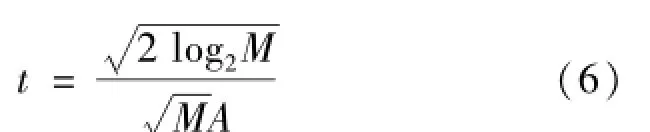
图4所示为经过带通滤波和小波包变换对Chirp信号响应数据去噪后，进行FFT分析与处理得到的二阶系统频率特性曲线。可见，经过带通滤波的响应数据进行小波包变换去噪后获得的频率特性曲线，明显优于图3所示的响应数据未经过处理获得的频率特性曲线。

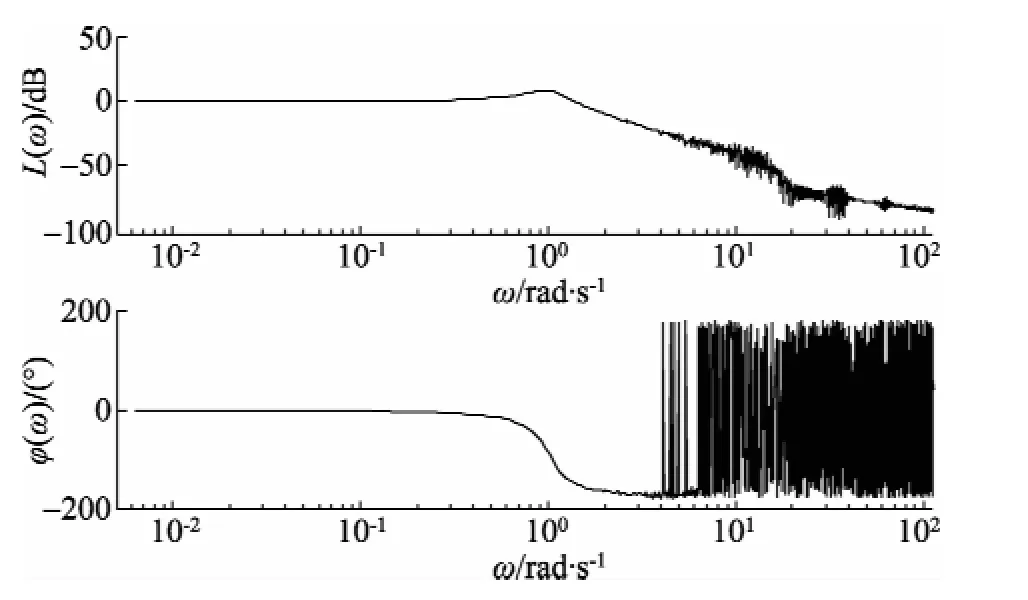
图4 滤波后系统频率特性曲线

6 实验研究

利用电阻、电容和运算放大器等电子元件搭建二阶线性电路作为被测试物理系统，如图5所示，其中运算放大器的型号为OP07CP，其它元件实测参数在图5中已标出。二阶电路系统ξ＝0.8，ωn＝12.5，传递函数为：

在Matlab环境下建立基于xPC Target的频率特性测试系统，xPC Target采用了宿主机-目标机的模式，目标PC机选用研华公司的IPC-610型工控机，与宿主机（普通笔记本电脑）用交叉线型的以太网电缆进行连接。目标机测控板卡选用研华公司PCI-1712，其中A／D和D／A的分辨率为12位。真实的实验系统照片如图6所示。

图5 二阶系统模拟电路

系统频率特性测试范围为0.001～20 Hz，采样频率为1000 Hz，数据长度为217。当输入Chirp信号幅值为0.5 V时，由于电路零偏影响，响应信号包含一个大约为0.21 V的稳态直流分量。在系统响应输出信号中加入白噪声作为测量噪声，使得信噪比为－10 dB。采用带通下限截止频率和带通上限截止频率分别为0.001 rad·s－1和20 rad·s－1的带通滤波器，运用基于Sym8小波函数的浮动阈值小波包变换对经过带通滤波后的典型二阶系统Chirp信号响应数据进行去噪处理，测试系统频率特性曲线，测试结果如图7所示。

图6 真实的实验系统照片

系统频率特性曲线的精度主要考查系统性能评价和控制器设计的重要频段［0，ωc］的测试精度和重复精度，ωc为系统截止频率。以偏离理想频率特性曲线最大点处的误差作为测试精度；同一系统在相同条件下，多次测量结果之间的平均差值作为系统频率特性测试的重复精度。以不加入白噪声并滤除稳态直流分量得到的频率特性曲线作为理想频率特性曲线，将信噪比继续降低，分析在信噪比分别为1 dB、－5 dB、－10 dB、－20 dB的测试精度和重复测量5次的重复精度，如表1所示。

表1 不同信噪比下测试精度分析

由此可知，在真实系统中，信噪比不低于－20 dB时，应用本文方法，幅频特性曲线测试精度在不低于1 dB，重复精度不超过0.03 dB；相频特性曲线测试精度不低于3°，重复精度不超过0.4°，完全可以满足系统性能评价和控制器设计的应用要求。

7 结 论

本文在低信噪比背景下，基于系统对Chirp信号的响应过程，采用带通滤波和小波包变换去噪对系统信号进行预处理，再由FFT进行分析和处理，获得系统频率特性曲线，从而完成系统频率特性测试。

（1）本方法可以有效滤除测量通道干扰造成的噪声和采样A／D分辨率不足所带来的采样量化噪声，降低系统对测量通道抗干扰的要求和对采样系统A／D分辨率的要求。

（2）采用带通滤波器滤除了系统的稳态直流分量，避免了频谱的重复和混叠的情况，还可以滤掉高频干扰信号，为之后的小波包变换减少运算量。

（3）在信噪比＜10 dB的情况下，采用小波包变换对响应信号进行去噪处理，可以有效提取系统真实响应信号，提高获得系统频率特性曲线的精度。

（4）本方法的有效性在典型二阶系统模拟电路的实验中得到全面验证，特别是在控制系统性能评价和控制器的设计过程中，低于截止频率的频段，信噪比不低于－20 dB时，其幅频特性曲线测试精度不低于1 dB，重复精度不超过0.03 dB；相频特性曲线测试精度不低于3°，重复精度不超过0.4°，完全可以满足系统性能评价和控制器设计的应用要求。

［1］ 陈平，裘丽华.液压伺服系统测试的谱分析法研究［J］.机床与液压，2002，（1）：101－141.

［2］ 叶齐鑫，侯国屏，赵伟.虚拟仪器环境下的频率特性测试方法［J］.电测与仪器，2005，22（2）：1－3.

［3］ 张群英，杨雪贤，何佩琨，等.A／D量化误差对脉冲压缩结果的影响［J］.现代雷达，2002，42（6）：64－68.

［4］ 范显峰，姜兴渭.基于小波包变换的信号去噪方法研究［J］.哈尔滨工业大学学报，2003，35（7）：809－811.

［5］ 黄宜军，汪金友.小波分析在微弱信号测量中的应用研究［J］.计量学报，2007，28（2）：163－166.

［6］ 王玥萌.频率特性综合测试系统的研究和设计［D］.哈尔滨：哈尔滨工业大学，2012.

［7］ Wang Q G，Hang C C，Bi Q.Process Frequency Response Estimation from Relay Feedback［J］.Control Engineering Practice，1997，5（9）：1293－1302.

A MeasurementMethod of Frequency Response Characteristics Test Based on Chirp Signalat Low SNR

WEILie-jiang1， LIXu-fang1， WANG Lin1， DONGWan-yu1， MENG Li2
（1.School of Energy and Power Engineering，Lanzhou University of Technology，Lanzhou，Gansu 730050，China；
2.Gansu Institute of Metrology，Lanzhou，Gansu 730070，China）

A method using band-pass filter and wavelet packet transform to pre-treat signal and then using FFT analysis and treatment to get frequency response diagrams is described.Thismethod is better to solve the problems that frequency characteristic testof the system isunder low SNR，and reduce hardware requirements of acquisition system in the test.The research show thatwhen SNR is very low and even negative 20 dB value，the amplitude-frequency characteristic that accuracy is not less than 1dB and phase frequency response curve that accuracy is not less than 3°can be obtained for frequency bands that is below the cutoff frequency，which fully meet the system performance evaluation and controller design app lication requirements.

Metrology；Frequency characteristics；Wavelet packet transform；FFT

TB973

A

1000-1158（2014）03-0272-04

10．3969／j．issn．1000-1158．2014．03．16

2013-09-23；

2013-12-30

国家自然科学基金（51365208）；863计划项目（2012AA052903）

魏列江（1972－），男，甘肃皋兰人，兰州理工大学副教授，博士，主要从事流体测控方面的研究。weiliejiang＠126.com