成像距离对图像畸变系数的影响研究

潘 慧， 汪 敏， 徐建亮， 刘晓辉， 许四祥

（安徽工业大学工程实践与创新教育中心，安徽马鞍山 243002）

成像距离对图像畸变系数的影响研究

潘 慧， 汪 敏， 徐建亮， 刘晓辉， 许四祥

（安徽工业大学工程实践与创新教育中心，安徽马鞍山 243002）

基于共线特征点求解图像畸变系数的方法，研究了拍摄物体平面与镜头平面间的不同距离参数对图像畸变系数的影响，并结合实验结果探寻了畸变系数的变化规律。在此基础上，指出镜头的畸变系数不仅与焦距有关，成像距离也是重要的影响因素，不可忽略。进行了不同距离参数下的畸变系数对相同标准量块图像校正的实验研究，比较了不同畸变系数下校正量块图像的不同高度位置的宽度曲线。实验结果表明，不同距离参数下的畸变参数对量块图像进行校正的结果是不同的，且当选用的畸变参数的距离与实际的成像距离相同时，其校正结果的精度最高，量块图像宽度测量的精度最高。

计量学；成像距离；畸变系数；校正；测量精度

1 引 言

在机器视觉中，光学镜头畸变的存在导致成像模型与针孔模型不一致［1，2］，拍摄出的图像会存在几何失真，因此，对图像畸变的研究是机器视觉中一个非常重要的课题。图像的畸变存在径向畸变和切向畸变，一般而言，图像的切向畸变比较小，大多只需要考虑径向畸变［3～5］。目前对畸变系数的研究方法很多，大体分为两类：一类是综合标定法［4］，即将图像的非线性畸变的求解和相机的内、外参数的求解综合在一起，该方法需要知道物体的空间坐标，并且求解过程复杂。另一类是垂轴法［6～9］，该方法让光学系统光轴垂直于网格标定板，依据针孔模型的原理，求解图像的畸变系数。畸变虽然不影响图像的清晰度，但是当利用像的大小来测量物体大小时，畸变的存在会直接影响测量精度，消除畸变是一个必须的工作。本文采用特制的棋盘格标定板，应用透视投影不变性原理，依据共线特征点投影后依然共线的原理［10］求解图像的畸变参数，对图像进行畸变校正。文献［11，12］认为，图像的畸变系数仅与焦距有关，文献［13］认为，定焦相机焦距的微调会引起图像畸变系数的微小改变，但变化很小，可以认为是常数。除了焦距的影响外，其它外界因素对图像的畸变系数也会产生影响。本文主要研究成像距离对图像畸变系数的影响，即研究拍摄物体平面与镜头平面间的不同距离情况下图像畸变系数的变化规律，并将不同距离参数下的畸变系数对相同标准量块图像进行畸变校正，并获得量块图像的边界，进而得到量块图像在不同高度位置上的宽度值，通过对量块不同高度位置上的宽度值进行详细的数据分析和图表比较，分析得出不同距离参数下畸变系数对量块校正结果精度的影响。

2 图像校正原理

2.1 图像畸变模型

目前在图像测量领域应用最广泛的是摄像机透视投影成像模型，这种模型在物理上相当于薄透镜成像，其最大优点是成像性能是线性的。本文只考虑一阶径向畸变，其模型如式（1）所示。

式中：xu，yu为理想图像坐标；xd，yd为畸变图像坐标。

2.2 畸变参数估计原理

根据透视投影原理，三维场景中一条直线经过透视后在图像平面中应该也为一条直线，但是在实际拍摄过程中，由于畸变的存在，导致三维场景中的直线在图像平面中会弯曲。图像参数估计的原理就是依据直线的透视不变性，即三维场景中的直线与图像平面的曲线的对应关系来估计图像的畸变系数。本文选用棋盘格标定板来进行计算，图1是畸变图像，应用角点检测算法得到畸变图像的图像坐标（xd，yd），理想图像（未发生畸变的图像）坐标为（xu，yu）。由于（xd，yd）与（xu，yu）之间存在偏差，所以三维场景中的直线在图像平面中不能仍为直线。畸变系数的估计正是利用这一特性建立优化函数。

图1 畸变图像

利用角点检测算法求出畸变图像的图像坐标，设为Bij，表示的是第i行第j列的角点（0＜i＜b，0＜j＜bi），其中，b为畸变图像特征点的行数，而每一行则由bi个角点组成。利用式（1）可求出无畸变图像的坐标为Uij，拟合无畸变图像的坐标得到m条直线，设为Li，理想图像中点到直线的距离为|Uij－Li |则点到直线的距离之和最小即为求畸变参数的优化函数，见式（2）：

采用L-M方法对式（2）进行优化，即可求出图像的畸变系数k。求出畸变系数以后，对图1进行畸变校正，校正后的图像如图2所示。

图2 校正后图像

3 图像畸变系数变化规律

3.1 距离对畸变系数的影响

为研究镜头平面与拍摄物体平面间距离参数对图像畸变系数的影响规律，本文特进行实验：在物体平面到相机镜头平面的距离分别为140 mm、160 mm、180 mm、200 mm、220 mm、240 mm、260 mm、280 mm的位置上对棋盘格标定板进行成像，并在相同距离位置上进行3次成像，即在每个距离参数下获取3幅图像，总共获取了24幅图像。如图3中3幅图像分别为物体平面到相机镜头平面的距离为200mm时3次成像所获取的图像。实验中，采用的棋盘格标定板型号为VCBC-75-1-X，精度为0.001 mm，使用的CCD相机型号为CM-140MCL，镜头为Compuar，其焦距为25 mm。

图3 距离为200mm时3次拍摄棋盘格标定板图像

获取图3图像后，应用亚像素角点检测算法对这些获取的图像分别进行检测计算，即可获取图像中各角点的精确坐标。图3中图像的角点检测结果如图4所示，图4中，“○”表示检测到的各角点位置。在进行角点检测计算时，由于图像边缘点易受到边界环境的影响，为了保证检测结果精度，不对这些位于边缘位置的角点进行检测计算。

图4 图3中图像的角点检测结果

基于各幅图像中计算得到的角点位置坐标，根据式（2）的迭代计算即可获取不同图像的畸变系数，8组不同距离参数下的24幅图像的畸变系数计算结果如表1所示。表1中，d为镜头平面到拍摄物体间的距离参数；Ⅰ、Ⅱ、Ⅲ分别表示相同距离参数下3次拍摄所获得的图像的畸变系数。

通过表1中的8组不同距离参数下的图像畸变系数值可知，当距离参数不变时，三次拍摄所得图像的畸变系数相差很小，其中变化最大值为0.000 2，由此可以认为，当距离参数确定时，其图像的畸变系数也是不变的。同时由表1可知，当距离为最小时，图像的畸变系数为最大；当距离为最大时，图像的畸变系数最小；且随着距离参数的增大，图像的畸变系数是单调递减的；由此可知，距离参数的变化将引起图像畸变系数值的改变，且图像畸变系数值的变化显著，如距离参数分别为140 mm和280 mm时，所获得图像的畸变系数值的差值达到0.005 7，即d＝140 mm时所获得图像的畸变系数是d＝280 mm时所获得图像的畸变系数的近似2倍。

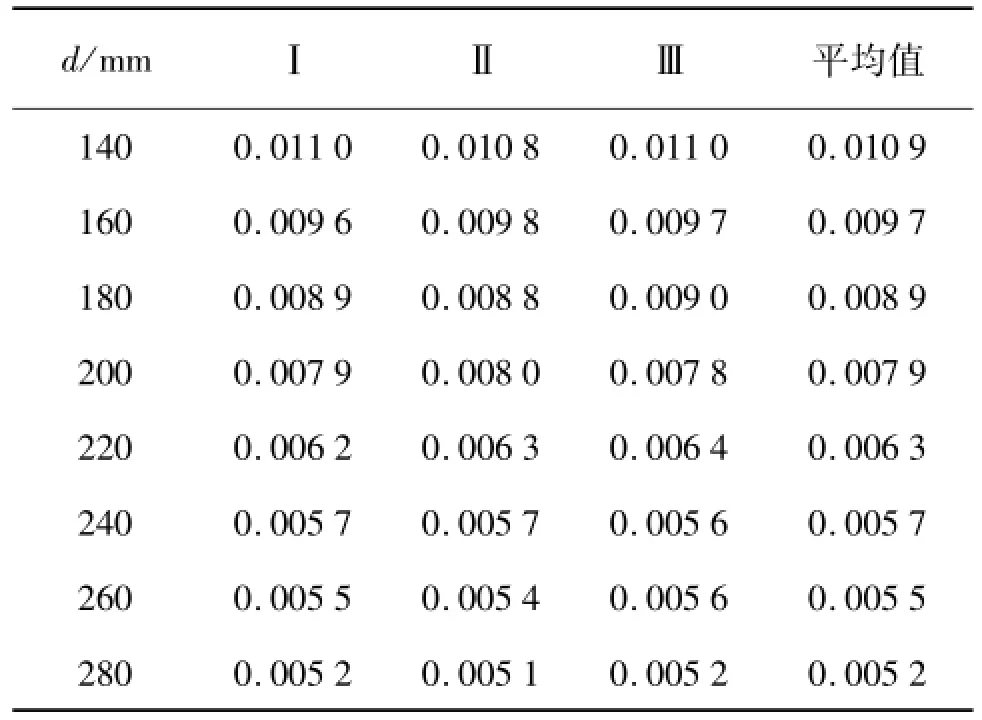
表1 不同距离参数下24幅图像的畸变系数表

为更清楚地反映距离参数与图像畸变系数之间的变化关系，对表1中的平均值进行曲线拟合，拟合后的曲线如图5所示。图5中的横坐标表示拍摄物体平面到镜头平面间的距离，纵坐标表示相同距离参数下3次拍摄所获得图像的畸变系数的平均值。由图5可明显看出，随着拍摄图像与相机镜头间距离的逐渐增大，图像的畸变系数逐渐减小，且呈现出非线性单调递减的变化关系。

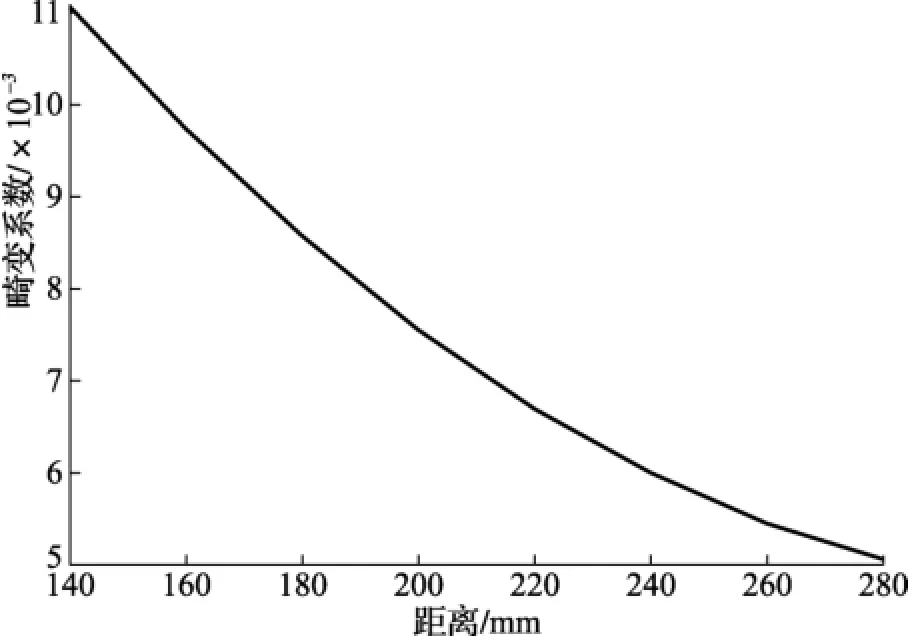
图5 畸变系数拟合曲线

3.2 不同距离参数下畸变系数校正相同图像实验

为了进一步分析不同距离参数下图像畸变系数对图像校正结果的影响，现进行以下实验研究：即首先获取待校正的原始图像，实验中选取的成像对象为80mm×35 mm×10mm的标准量块，成像的具体过程为，先调节相机镜头平面与量块间的距离，当成像距离为200 mm时，对量块进行成像并保存，获得的图像如图6所示，图像大小为1 280 pixel×1 024 pixel，这里需说明的是，该实验的成像条件与本文中第3.1节中描述的棋盘格标定板在距离为200 mm的成像条件完全一致，由此，参照表1可知该条件下量块图像的畸变系数为0.007 9。下面分别用3种不同距离参数下的图像畸变系数（分别为0.007 9、0.010 9以及0.005 2）对图6所示图像进行畸变校正，并对图6及3种不同畸变系数条件下得到的畸变校正幅图像进行边界检测计算，得到量块左右两边缘的边界线，再基于宽度计算公式，即可获得不同高度位置上的量块宽度值，其结果如图7所示。

图6 量块原图

图7 不同高度位置时量块图像的宽度曲线

图7中的横坐标行数表示量块的高度位置，纵坐标表示量块的宽度值。由图7可知，当对量块图像不进行校正，直接应用边界检测算法进行计算时，所获得量块宽度值不精确，此时获得的不同高度上量块的宽度值是不均匀的，且呈现出凸形，明显不合理；用k＝0.007 9、k＝0.010 9、k＝0.005 2分别对量块图像进行畸变校正，对校正后的图像应用边界检测计算获得量块的宽度值，从图7中可看出量块的宽度均匀性均有所提高，且从图7中还可看出，当k＝0.007 9即选用畸变系数的距离与实际的成像距离相同时，得到的量块校正图像的宽度值分布均匀性最好，图像的校正精度最高。为进一步对量块校正图像进行比较，对图6中量块图像得到的不同高度位置上的量块宽度曲线进行数据分析，见表2。

表2 不同高度量块图像宽度值数据分析

表2中，Wmin为图7中4幅图像求得的量块图像不同高度位置上的宽度最小值，Wmax为最大值；Δ＝Wmax－Wmin；δ为量块宽度值的方差。从表2中可看出，未进行畸变校正的量块图像，Δ和δ都最大，Δ最大表示量块图像在不同高度位置上的宽度值变化范围最大，δ表示量块图像在不同高度位置上的宽度值波动最大，最不稳定。而k＝0.007 9时的量块校正图像在不同高度位置上的宽度值Δ和δ都最小，表明量块图像在不同高度位置上的宽度值变化范围最小，同时波动范围最小，数据最为稳定。未被校正的量块图像在不同高度位置上的宽度分布是很不均匀的，量块的宽度值精度比较低，用不同距离参数下的畸变系数对量块图像进行校正以后，不同高度位置上量块图像的宽度值精度均有所提高，且当选用的畸变系数的距离与实际的成像距离相同时，校正后量块图像在不同高度位置上的宽度值的精度最高，校正效果最好。

4 结 论

研究了不同距离参数下图像畸变系数的变化规律。图像的畸变系数随成像距离的逐渐增大而逐渐减小，并且呈现出非线性单调递减的变化关系。进行了不同距离参数下得出的畸变系数对量块的校正实验，实验结果表明：只有当选用的畸变系数的距离与实际的成像距离相同时，图像的校正精度才能达到最高。成像距离是影响图像畸变的重要因素，在实际测量，定焦相机镜头畸变系数不可作为常数，应当考虑成像距离的影响。

［1］ 段发阶，张健新，叶声华.CCD摄像机参数标定新技术［J］.计量学报，1997，18（4）：294－299.

［2］ Weng J，Cohen P，Herniou M.Camera calibration with distortion models and accuracy evaluation［J］.IEEE Trans．Pattern Analysis Machine Intelligence，1992，14（10）：965－980.

［3］ Ahmed M，Farag A.Nonmetric calibration of camera lens distortion：Differentialmethods and robust estimation［J］.IEEE Transaction on Image Processing，2005，14（8）：1215－1230.

［4］ 黄桂平，李广云，王保丰，等.单目视觉测量技术研究［J］.计量学报，2004，25（4）：314－317.

［5］ 杨必武，郭晓松.摄像机镜头非线性畸变校正方法综述［J］.中国图象图形学报，2005，10（3）：269－274.

［6］ Weng J，Cohen P，Herniou M.Camera calibration with distortion models and accuracy evaluation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14（10）：956－980.

［7］ Chao Zhang，Helferty J P，McLennan G，et al. Nonlinear distortion correction in endoscopic video images［C］／／Image Processing 2000 International Conference. 2000，2：439－442.

［8］ 姜大志，孙俊兰，郁倩，等.标准图形法求解相机镜头非线性畸变的研究［J］.东南大学学报，2001，31（4）：111－116.

［9］ 孔明，王式民.共轴法立体视觉三维测量的研究［J］.计量学报，2004，25（4）：294－297.

［10］ 周富强，胡坤，张广军.基于共线特征点的摄像机镜头畸变校正［J］.机械工程学报，2006，42（9）：174－177.

［11］ 郑毅，刘上乾.利用直线特征的定标图像非线性畸变校正［J］.仪器仪表学报，2007，28（6）：1129－1133.

［12］ 李欢，孙茂印，汤晓安，等.一种新的基于规则点阵的图像畸变校正方法［J］.仪器仪表学报，2004，25（4）：581－582.

［13］ 周富强蔡斐华.基于非量测畸变校正的摄像机标定方法［J］.机械工程学报，2009，45（8）：228－232.

Study on the Influence Rule of Different Imaging Distance to Distortion Coefficients

PAN Hui， WANGMin， XU Jian-liang， LIU Xiao-hui， XU Si-xiang
（Engineering Practice and Innovation Education Center，Anhui University of Technology，Maanshan，Anhui243002，China）

Based on the approach to estimate the image distortion coefficients through a set of collinear pints，the influence of the distance between the object plane and the lens plane on the image distortion coefficients is studied. Combined with the experimental result，the change rule of the distortion coefficients is explored.Then，the influence of the distortion coefficients（under various distances between the object plane and the lens plane）on the correction of the same gauge block is experimentally researched.The experimental results show that the correction results of gauge block image are different under different parameters of distortion coefficients.Only when the chosen distance in the distortion parameters is the same as the real imaging distance，the correction precision is the highest，and themeasured accuracy of the gauge is also the highest.

Metrology；Distortion coefficients；Imaging distance；Correction；Measure accuracy

TB96

A

1000-1158（2014）03-0221-05

10．3969／j．issn．1000-1158．2014．03．06

2013-01-21；

2013-04-09

国家自然科学基金（10702001）；安徽省优秀青年科技基金项目（10040606Y23）；安徽省教育厅项目（KJ2009A0172）

作者简介：潘慧（1986－），女，安徽安庆人，安徽工业大学助理实验师，研究方向为数控技术研究，基于图像的高精度测量。panhui123＠ahut.edu.cn