基于球杆仪的旋转轴几何误差测量和辨识

陈剑雄， 林述温， 韩国强，2

（1.福州大学机械工程及自动化学院，福建福州 350108；2.中国科学院福建物质结构研究所，福建福州 350002）

基于球杆仪的旋转轴几何误差测量和辨识

陈剑雄1， 林述温1， 韩国强1，2

（1.福州大学机械工程及自动化学院，福建福州 350108；2.中国科学院福建物质结构研究所，福建福州 350002）

通过圆弧测量轨迹，移动球杆仪测量球心在旋转工作台上3个安装位置的9项误差，采用齐次变换理论建立几何误差辨识模型，引入系数矩阵条件数进行安装参数的优化选取，提出一种辨识旋转轴4项位置和6项运动误差的方法。最后，在四轴数控加工中心上进行了测量和验证实验，该方法可辨识出全部的几何误差项，通过对几何误差计算出的预测值和球杆仪的测量值的比较，预测值的绝对误差小于0.003 mm，具有辨识精度高、测量省时的优点。

计量学；旋转轴；几何误差；球杆仪；条件数

1 引 言

数控回转工作台是多轴数控机床的重要组成部分，由于其零部件在制造、装配的精度有限或者使用过程发生磨损等因素，存在不可避免的几何误差，对数控机床的加工精度具有显著的影响［1，2］。根据ISO 230-7（2011）［3］的定义，旋转轴的几何误差分为4项轴线位置和6项运动误差。对于轴线的位置误差，主要通过多轴联动的测量轨迹，采用球杆仪［4～6］、3D测头［7］、4D测头［8］或电容测头［9］等精密仪器进行测量和辨识。这些方法忽略了与位置有关的运动误差，并不能准确反映旋转轴的几何误差空间分布情况。对于旋转轴运动误差的测量，有关研究［10］采用多面体棱镜、激光自准仪和LVDT等精密仪器进行直接测量，但是对旋转轴的安装位置有特殊的要求，安装和调整困难，测量效率低。近年来，出现了一些商业化的旋转轴运动误差测量仪器［11］，价格较昂贵，而且只能测量部分运动误差项目。因此，有必要研究一种快速简单的、能够在机床上直接测量和辨识旋转轴全部位置和运动误差项目的方法。

本文提出一种采用球杆仪测量和辨识旋转轴位置和运动误差的方法。将球杆仪一端的球心分别安装在旋转工作台的3个不同位置，移动球杆仪另一端球心按圆形轨迹运动，依次测量每个球心位置在X、Y、Z这3个方向上由旋转轴几何误差产生的偏差。根据这9项测量值采用齐次变换理论建立起几何误差的辨识模型。同时引入条件数对球杆仪的安装参数进行评价，实现了安装参数选取的优化。在此基础上，分两步从球杆仪测量结果中辨识出4项轴线位置误差和6项运动误差。最后，在四轴数控机床上采用球杆仪进行了测量和验证实验，通过比较球杆仪的实际测量值与由辨识出的几何误差计算的预测值，并与现有的采用球杆仪辨识方法的预测精度进行对比，验证所提出的辨识方法的有效性和辨识结果的正确性。

2 测量方法与辨识模型

应用球杆仪进行测量时，将球杆仪一端固定在主轴上，另一端安装在旋转轴的工作台面上。如图1所示，由于旋转轴的几何误差会使得球座位置产生偏移，球杆仪一端球心Ps的位置也随之变化，可用变化量［dxs，dys，dzs］表示。通过主轴移动球杆仪绕Ps沿圆弧测量轨迹至坐标轴方向，即误差敏感方向，可依次测量出球心偏差。由于在一个球心的测量点处只能获得3个偏移量，还需额外的测点才能够求解6项误差。以一台四轴联动的数控加工中心为例，在A轴转动角度不变的情况下，选择3个不同的球座位置作为测点。

图1 采用球杆仪测量球心偏差

球座测量点分布如图2所示，旋转轴坐标系的坐标轴方向与机床参考坐标系一致，原点位于A轴轴线与工作台面的交点。3个测点Ps1、Ps2和Ps3分布在半径为R的圆周上，初始位置的坐标分别为（－H，0，R）、（－H，R，0）和（－H，－R，0）。球心距离工作台面的高度为H。在不同旋转角度下，利用球杆仪可依次测得这3个测点处的9个球心偏差。对于球杆仪在移动过程中由直线轴运动产生的误差，可预先进行补偿［12］。所以这些测量值可全部视为旋转轴位置和运动误差的综合。

图2 球座测量点分布

为了从球心偏差的测量值中分离出位置与运动误差，可将误差辨识的过程分为两个步骤。首先，由于位置误差是常数，可将测量值视为全部由位置误差引起的结果。当旋转轴转到第i个测量角度αi时，若测量值为［dxs1i，dys1i，dzs1i，dxs2i，dys2i，dzs2i，dxs3i，dys3i，dzs3i］T，用［Yoa，Zoa，Boa，Coa］T表示A轴轴线位置在Y、Z方向的线性误差及与绕Y、Z轴的角度误差，于是采用齐次变换理论可建立起球心偏差与轴线位置误差的超静定线性方程组：

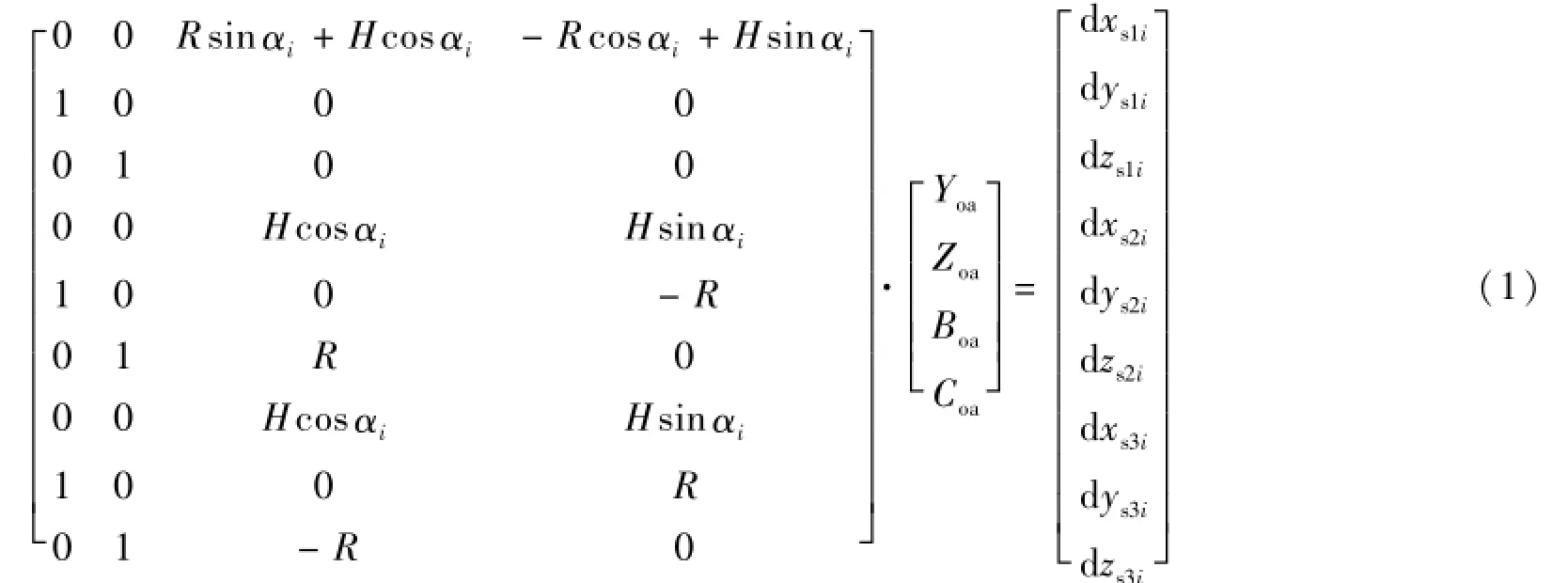
若用Aoi表示系数矩阵，Bi表示测量值，Xo为位置误差矢量，由所有n个测量角度下球心偏差的测量值可构建起位置误差的辨识模型：

［Ao1；Ao2；…；Aon］Xo＝［B1；B2；…；Bn］（2）

接着将位置误差引起球心偏差的部分从测量值中扣除，剩余部分可视为旋转轴运动误差的综合。若用误差矢量［δaxi，δayi，δazi，εaxi，εayi，εazi］T表示第i个测量角度αi时，A轴分别沿X、Y、Z方向的线性误差和绕X、Y、Z轴的角度误差，参照式（1），可得到运动误差的方程组：

若用Ai表示系数矩阵，Xi表示第i个测量角度下的运动误差，用线性方程的形式表示式（3）可得：

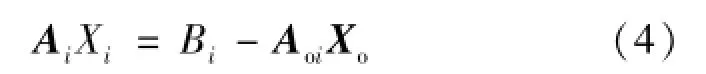
对于式（2）和式（4）的辨识模型，可采用系数矩阵的广义逆的方法，得到误差项的最小二乘解。在求解过程中，旋转轴的转动角度α，安装参数R和H对系数矩阵有重要的影响，也决定了方程的可解性以及解的稳定性。因此，本文引入条件数评价在不同转动角度下安装参数对系数矩阵的影响，并对安装参数的选择进行优化。根据文献［13］，求解广义逆时系数矩阵ATA的条件数可表示为：

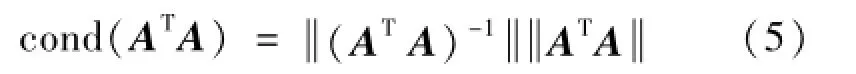
为了简化计算过程，采用∞范数来表示系数矩阵的条件数。考虑到安装参数中，球座上球心与工作台面之间的距离H调节范围仅为70 mm～90 mm，可当作常数处理，在实际测量时H值设置为80 mm。于是R值的选择可表示为优化问题，即选择最优的R值，使得条件数最小，可表示为：

通过计算仿真，在不同转动角度下条件数随R值变化的规律如图3所示。

从图3中可以看出，在不同的旋转角度下，系数矩阵的条件数首先随R值增大而急剧减小，随后又平缓上升。显然，不同角度下都存在一个最优R值使得条件数最小。另外，从图4中可以看出，R值的选取随旋转角度的变化而变化。如果在实际测量时在不同角度下都采用优化后的R值进行测量，安装和调整的过程将会非常繁琐。考虑到各角度下的最优R值变化幅度不大，而且R值的微小变化并不会引起条件数突变，因此本文采用所有角度下最优R值的平均值，即92.902 mm作为最终的安装参数。

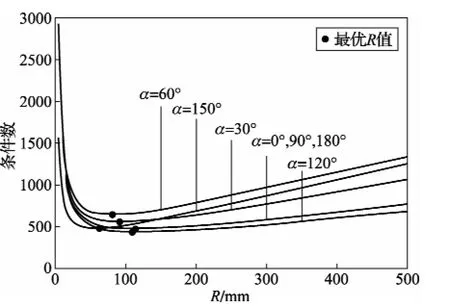
图3 不同旋转角度下条件数随R值变化的规律

图4 不同旋转角度下最佳R值的变化曲线

3 测量与验证实验

测量和验证实验在一台型号为XH715D的四轴立式加工中心上进行。为了避免测量过程中球座处于Z轴方向最低处时，主轴与旋转工作台发生干涉，球杆仪需加装50 mm的延长杆，而3个测点半径R根据上述的优化结果设置为92.902mm。在验证实验中球杆仪需加装200 mm的延长杆，3个测点半径R调整为102.606mm，以满足使用手册中规定的球杆仪轴线与球座轴线的夹角应大于70°的要求。测量和验证实验的安装参数见表1，图5为测量过程中的球杆仪的安装示意图，测量开始前先将一个球座安装到旋转工作台Ps1点处，另外一个球座安装在刀柄上。调整好位置后，将型号为QC20－W的球杆仪安装到两球座的球心处，这时球杆仪的轴线恰好平行于X轴。

图5 测量过程中的球杆仪的安装示意图

随后由主轴带动球杆仪在XY、YZ和XZ平面绕工作台上球座的球心做圆弧运动，使得球杆仪轴线依次平行于Y轴、Z轴和X轴。当球杆仪到达坐标轴方向时暂停6 s，以便从计算机中读取球心的偏差值。为了减少测量过程中安装和调整的时间，测量完一个测点的3个偏差后，由Y轴、Z轴和A轴联动，将球杆仪和球座同时移动到下一个测量角度，重复上述测量过程直到旋转轴转过一周。接着，重新调整底座位置到另外两个测点Ps2和Ps3并重复测量。整个测量过程可在机床上直接完成，只需安装和调整球杆仪的3次位置。而且采用圆弧测量轨迹，易于编程，能有效简化测量步骤，减少测量时间。

表1 实验安装参数mm

为了验证所提出的旋转轴几何误差辨识方法的有效性，同样以这台四轴联动数控机床为研究对象，设计了只有旋转轴运动的验证实验。参照图5，依照表1中的验证实验安装参数将球杆仪安装在机床上，其主轴端的球心位于A轴轴线上且保持静止。由旋转轴转动带动球杆仪绕A轴旋转。由于存在几何误差，球杆仪两端的距离会发生变化，这个变化量可视为旋转轴各项几何误差的综合。于是，通过辨识出来的几何误差，可对这个距离变化量进行预测。将预测结果与实际测量进行比较，即可验证所辨识出的误差的正确性。

4 结果与分析

测量实验过程中，旋转轴从0°开始，每转过5°从计算机中读取球心偏差。对于所有的3个测点，每个测点都进行了72次测量。为了尽量消除测量过程由于读数或者操作不当引起的测量误差，测量实验重复5次，并以5次测量的平均值作为最终测量结果，见图6。

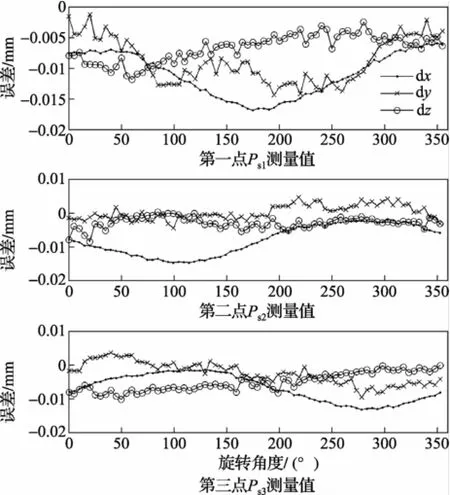
图6 工作台上球座在3个测点处的测量结果

将图6中的测量结果依次代入式（2）和式（4），即可辨识出旋转轴运动误差和位置误差。辨识结果如图7及表2所示。

图7 旋转轴运动误差的辨识结果

在验证实验中，旋转轴每转过5°从计算机中读取球杆仪两球心间距离的偏差。同时，采用辨识出的几何误差可对球杆仪的测量值进行预测，通过将预测结果与实际测量值的进行对比，可对辨识结果的正确性进行验证。另外，为了与现有基于球杆仪的方法进行对比，也单独采用位置误差对偏差值进行预测。如图8所示，如果只考虑旋转轴的位置误差，虽然预测值跟测量值的变化规律基本一致，但预测值的误差较大，最大值达到0.011 mm。而采用本文的方法，如图9所示，预测值与测量值变化规律相同，曲线形状一致，而且预测值的绝对误差值不超过0.003 mm，比现有的只考虑位置误差的方法具有更高的精度，可满足高精度的误差辨识和补偿需求。

表2 旋转轴轴线位置误差辨识结果

图8 只考虑位置误差时预测值与测量值的比较结果

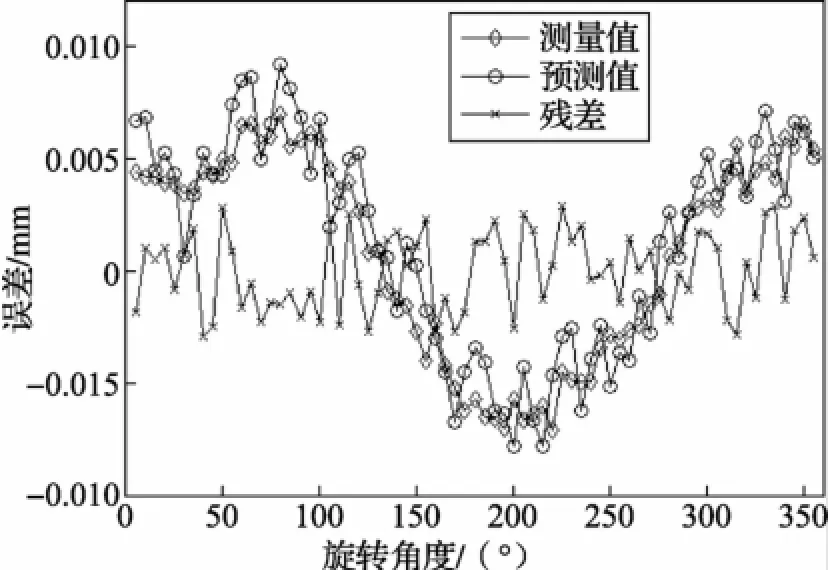
图9 考虑位置误差与运动误差时预测值与测量值的比较结果

5 结 论

通过圆弧轨迹将球杆仪移动至坐标轴方向，测量旋转工作台上的标准球球心在3个测点处的9项误差，简化了测量轨迹的编程，提高了测量效率。采用条件数对安装参数进行了优化，提高了求解误差项时数值计算的稳定性。运用齐次变换理论建立了几何误差的辨识模型，从测量实验的结果中辨识出了旋转轴全部的4项轴线位置和6项运动误差。在验证实验中，运用辨识出的几何误差对测试轨迹上的球杆仪两球心距离进行预测，并与现有的方法进行了对比。实验结果表明，采用本文所提出方法的预测值的绝对误差不超过0.003mm，比现有的方法具有更高预测精度。而且所需的仪器是工业现场广泛使用的球杆仪，可在机床上直接完成整个测量过程，有利于在工程实践中推广应用。

［1］ Schwenke H，Knapp W，Haitjema H，etal.Geometric error measurement and compensation of machines-An update［J］.CIRP Annals-Manufacturing Technology，2008，57（2）：660－675.

［2］ 杨建国，许黎明，刘行，等.加工中心的几何误差和热误差综合补偿模型［J］.计量学报，2001，22（2）：90－94.

［3］ ISO 230－7.Test Code for Machine Tools-Part 7：Geometric accuracy of axes of rotation［S］.Geneva：International Organization for Standardization，2011.

［4］ Tsutsumi M，Saito A.Identification and compensation of systematic deviations particular to 5-axis machining centers［J］.International Journal of Machine ToolsandManufacture，2003，43（8）：771－780.

［5］ 张大卫，商鹏，田延岭，等.五轴数控机床转动轴误差元素的球杆仪检测方法［J］.中国机械工程，2008，19（22）：2737－2741.

［6］ Lee K I，Lee DM，Yang SH.Parametricmodeling and estimation of geometric errors for a rotary axis using double ball-bar［J］.International Journal of Advanced Manufacturing Technology，2012，62（5）：741－750.

［7］ LeiW T，Hsu Y Y.Accuracy enhancement of five-axis CNC machines through real-time error compensation［J］.International Journal of Machine Tools and Manufacture，2003，43（9）：871－877.

［8］ Weikert S，Knapp W.R-Test，a New Device for Accuracy Measurements on Five Axis Machine Tools［J］.CIRP Annals-Manufacturing Technology，2004，53（1）：429－432.

［9］ Zargarbashi S H H，Mayer J R R.Single setup estimation of a five-axismachine tool eight link errors by programmed end point constraint and on the fly measurement with Capball sensor［J］.International Journal of Machine Tools and Manufacture，2009，49（10）：759－766.

［10］ Suh S H，Lee E S，Jung S Y.Error modeling and measurement for the rotary table of five-axis machine tools［J］.International Journal of Advanced Manufacturing Technology，1998，14（9）：656－663.

［11］ 王金栋，郭俊杰，费致根，等.基于激光跟踪仪的数控机床几何误差辨识方法［J］.机械工程学报，2011，47（14）：13－19.

［12］ 王一丁，张国雄，臧艳芬，等.数控加工中心的位置误差补偿模型［J］.计量学报，1995，16（3）：200－205.

［13］ 李庆扬，王能超，易大义.数值分析［M］.北京：清华大学出版社，2008，8－12.

Geom etric Error Measurement and Identification for Rotary Table Using Double Ballbar

CHEN Jian-xiong1， LIN Shu-wen1， HAN Guo-qiang1，2
（1.School of Mechanical Engineering and Automatic，Fuzhou University，Fuzhou，Fujian 350108，China；
2.Fujian Institute of Research on the Structure of Matter，Chinese Academy of Science，Fuzhou，Fujian 350002，China）

The derivations of the center of the ball installed on the rotary table aremeasured by double ballbar with circular paths in the error sensitive directions.Hence，there are nine resultsmeasured from threemounting positions of the ball at the same rotation angle，to form four axis location and six motion errors identification model using homogeneous transformation.In addition，the condition number is applied to select the optimum installation parameters of the ballbar. Finally，themeasurementand verification experiments are conducted on the four-axismachining center.All the elements of the geometric error can be identified by the proposed method from themeasured results with high accuracy and measuring effectively.Then，comparing the predicted value from the identified errors with themeasured results by ballbar，it shows that the absolute residual error is less than 0.003mm.

Metrology；Rotary axis；Geometric error；Double ballbar；Condition number

TB92

A

1000-1158（2014）03-0198-06

10．3969／j．issn．1000-1158．2014．03．02

2013-07-15；

2013-11-22

国家自然科学基金（51205063）；中国博士后基金（2012M521281，2013T60643）；福建省重大科技专项（2010HZ002-1）

陈剑雄（1981－），男，福建莆田人，福州大学讲师，博士研究生，主要从事数控系统、精密测量技术研究。jxchen045＠fzu.edu.cn