考虑矩震级影响的位移谱阻尼调整系数

王国弢 胡克旭 雷 敏

（同济大学结构工程与防灾研究所，上海200092）

考虑矩震级影响的位移谱阻尼调整系数

王国弢*胡克旭 雷 敏

（同济大学结构工程与防灾研究所，上海200092）

基于408条地震地面运动记录统计分析，首先研究了矩震级（Mw）对位移谱阻尼调整系数（DSF）的影响。结果表明：Mw对DSF的影响与周期（T）和阻尼比（ξ）有关；在T＞0.6 s的范围内，当ξ＜5%时，DSF随着Mw的增长而增长；当ξ＞5%时，DSF随着Mw的增长而减小。随着T的增长，Mw对DSF的影响越显著；ξ越远离5%，Mw对DSF的影响越显著。在T＜0.6 s的范围内，Mw对DSF无显著影响；当Mw＝5～6时，DSF受T的影响显著；随着Mw的增大，在T＞～0.6 s范围内，DSF受T的影响逐渐减弱；当Mw＝7～8时，在T＞0.6 s范围内，除阻尼比为0.5%和1%的DSF外，DSF基本不随T而变化；DSF相对于ξ存在异方差性。然后提出了只考虑周期和阻尼比影响的DSF回归方程，计算出在指定周期和阻尼比处的残差，根据在长周期处该回归方程的残差随Mw显直线分布，最后提出了包含线性矩震级项的DSF回归模型并给出了模型的回归系数。该模型的残差随Mw和相对能量持时（D5-95）的分布表明：模型能体现Mw对DSF的影响，能间接地体现D5-95对DSF的影响。模型的标准差能体现DSF相对于ξ的异方差性。

矩震级，阻尼调整系数，周期，阻尼比，重要持时

Keywordsmomentmagnitude，damping scaling factor，period，damping ratio，significant duration

1 引 言

在结构的抗震设计中需要不同阻尼比下的弹性反应谱。一般可采用两种方法来获得不同阻尼比下的弹性反应谱：①直接形成不同阻尼比下的反应谱预测方程；②采用阻尼调整系数将5%阻尼比的弹性反应谱调整到不同于5%阻尼比的弹性反应谱。各国抗震规范中普遍采用的是第二种方法。对于不同的反应谱，有不同的阻尼调整系数，本文所研究的阻尼调整系数为位移谱阻尼调整系数。近年来，对阻尼调整系数的研究表明：矩震级对阻尼调整系数有显著的影响；但中国和欧美现行抗震规范［1-6］中提供的阻尼调整系数只与阻尼比和结构自振周期有关或仅与阻尼比有关，不能反映矩震级对阻尼调整系数的影响。到目前为止，已有许多学者对阻尼调整系数进行了研究。Ashour［7］、Tolis和Faccioli［8］及Priestley［9］提出了仅考虑阻尼比影响的阻尼调整系数回归模型；Newmark和Hall［10］、Wu和Hanson［11］及Idriss［12］提出了考虑阻尼比和周期影响的阻尼调整系数回归模型。Lin和Chang［13］研究了场地条件对阻尼调整系数的影响，并提出了考虑阻尼比、周期和场地条件影响的阻尼调整系数回归模型。以上研究者所提出的回归模型均没有考虑矩震级对阻尼调整系数的影响。Bommer和Mendis［14］研究了矩震级对阻尼调整系数的影响，对阻尼比大于5%的情况，提出了阻尼调整系数随矩震级和观测点到断层面最近距离的增大而减小的结论；Cameron和Green［15］认为阻尼调整系数与地震动的频谱特性和持时有关并且他们将地面运动记录分别按地质构造环境、场地条件和震级进行分组，以表格的形式列出了在指定阻尼比和周期处的阻尼调整系数的中值和标准差，但他们均没有提出一个简单统一的能反映矩震级影响的回归模型。本文的研究目的是提出一个简单统一的阻尼调整系数回归模型并在模型中包含矩震级这个变量，使该模型能体现矩震级对阻尼调整系数的影响。此外，根据Kempton和Stewart［16］，持时与矩震级有正的强相关性，所以包含了矩震级的回归模型还可以间接体现持时对阻尼调整系数的影响。本文所采用的持时为相对能量持时D［17］5-95。

2 地面运动加速度时程记录

在本文的研究中使用了408条地震地面运动记录，这些地面运动记录下载于太平洋地震工程研究中心的强震数据库（http：／／peer.berkeley.edu／peer ground motion database）。地面运动记录的相对能量持时（D5-95）分布在1.4 s～80.3 s之间，矩震级（Mw）分布在5～7.62之间，观测点到断层破裂面的最近距离（Rrup）分布在0.1 km～100 km之间，地表厚度30 m内平均剪切波速（Vs30）分布在116.3 m／s～2 016.1 m／s之间，峰值地面加速度（PGA）分布在0.004 7 g～1.434 5 g之间。图1表明了本文所用记录的Mw和Rrup的分布。

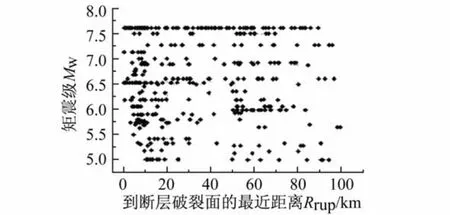
图1 Mw—Rrup分布Fig.1 Magnitude Vs.distance distribution

3 矩震级对阻尼调整系数的影响

式中，DSF代表位移谱阻尼调整系数；ξ代表阻尼比；T代表单自由度体系的自振周期；SD（ξ，T）和PSA（ξ，T）分别是ξ≠5%，周期为T时弹性单自由度体系的位移谱值和拟加速度谱值；SD（5%，T）和PSA（5%，T）分别是ξ＝5%，周期为T时弹性单自由度体系的位移谱值和拟加速度谱值。

本文采用软件SeismoSignal对每条输入地震波分别计算了11个阻尼比下位移谱。11个阻尼比分别为0.5%、1%、2%、3%、5%、7%、10%、15%、20%、25%和30%。对每个阻尼比，单自由度体系取如下20个周期：0.02 s、0.04 s、0.06 s、0.08 s、0.1 s、0.14 s、0.2 s、0.24 s、0.3 s、0.4 s、0.5 s、0.6 s、0.8 s、1 s、2 s、3 s、4 s、5 s、7.5 s和10 s。然后再根据式（1），对每条输入地震波可求

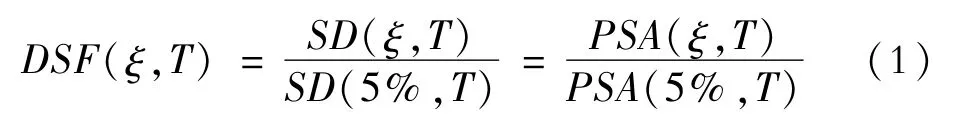
位移谱阻尼调整系数被定义为得各阻尼比下的位移谱阻尼调整系数。

为了研究Mw对DSF的影响，本文将地面运动记录按Mw分为三组，分组情况见表1。

表1 地面运动记录分组Table 1 Groups of ground motion records

图2表明了ξ＝0.5%、2%、7%和25%时，Mw对DSF中值的影响；图3表明了ξ＝1%、3%、10%和30%时，Mw对DSF中值的影响。由图2和图3可见，Mw对DSF的影响可归纳为以下几点：

（1）Mw对DSF的影响与T和ξ有关；在T＞0.6 s的范围内，当ξ＜5%时，DSF随着Mw的增长而增长；当ξ＞5%时，DSF随着Mw的增长而减小.

（2）随着T的增长，Mw对DSF的影响越显著；ξ越远离5%，Mw对DSF的影响越显著。在T＜0.6 s的范围内，Mw对DSF无显著影响.

（3）当Mw＝5～6时，DSF受T的影响显著；随着Mw的增大，在T＞0.6 s范围内，DSF受T的影响逐渐减弱；当Mw＝7～8时，除阻尼比为0.5%和1%的DSF外，在T＞0.6 s范围内，DSF基本不随T而变化。

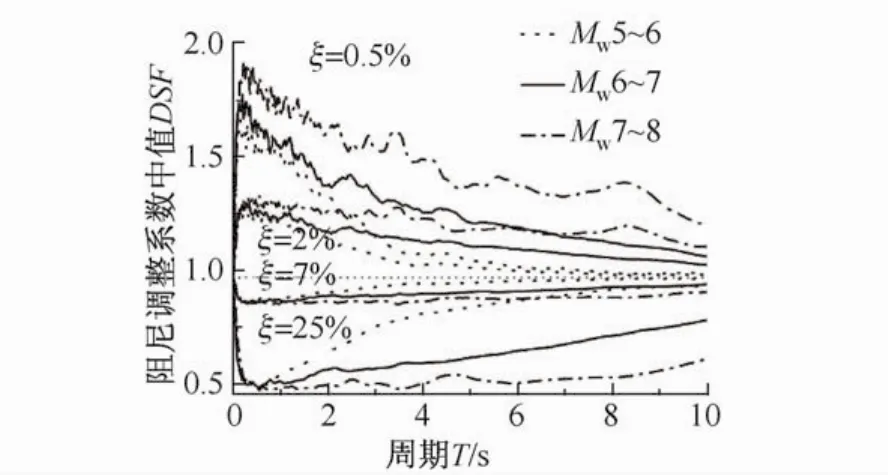
图2 Mw对DSF中值的影响（ξ＝0.5%、2%、7%和25%）Fig.2 Influence of Mwon themedian DSF（ξ＝0.5%、2%、7%and 25%）

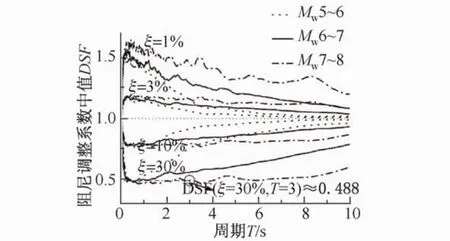
图3 Mw对DSF中值的影响（ξ＝1%、3%、10%和30%）Fig.3 Influence of Mwon themedian DSF（ξ＝1%、3%、10%和30%）

图4 给出了T＝1 s时，Mw与DSF之间的统计关系，图中直线为Mw和DSF的线性拟合线。由图4也可见：Mw对DSF的影响与ξ有关。此外，图4还表明了DSF相对于ξ的异方差性。随着ξ越远离5%，DSF的离散程度越大。DSF相对于ξ的异方差性将在后面的方差模型中考虑。

图4 Mw对DSF的影响Fig.4 Influence of Mwon DSF

综上所述，Mw对DSF有显著的影响，所以在DSF的回归模型中应考虑Mw的影响。

4 DSF的概率分布

通常可以认为PSA服从对数正态分布，对式（1）两边取自然对数有：

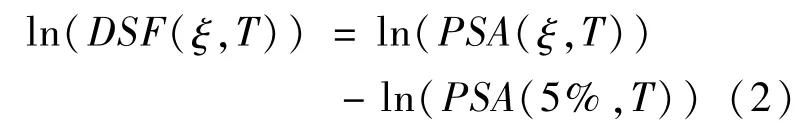
由式（2）可知，如果PSA（ξ，T）与PSA（5%，T）不相关，则ln（DSF（ξ，T））服从正态分布，DSF服从对数正态分布。但是，PSA（ξ，T）与PSA（5%，T）是相关的，所以在理论上DSF并不严格服从对数正态分布。根据对本文数据的分析，在T∈［0.1，7.5］的范围内，ln（DSF（ξ，T））与正态分布曲线拟合得较好。图5给出了ξ＝2%时，在T＝0.2 s和1 s处，ln（DSF）数据点的直方图、累积分布函数曲线图及相应的正态分布函数的拟合结果，图中CDF表示累积分布函数（cumulative distribution function），PDF表示概率密度函数（probability density function）。在此周期范围外，拟合结果并不理想。

综上，本文假设在指定的周期和阻尼比处，DSF近似服从对数正态分布，并取回归模型为

ln（DSF）＝μ（ξ，T，Mw）＋є（3）式中，μ（ξ，T，Mw）为ln（DSF）的期望；є代表随机误差且є服从正态分布N（0，σ2）；σ2为方差。

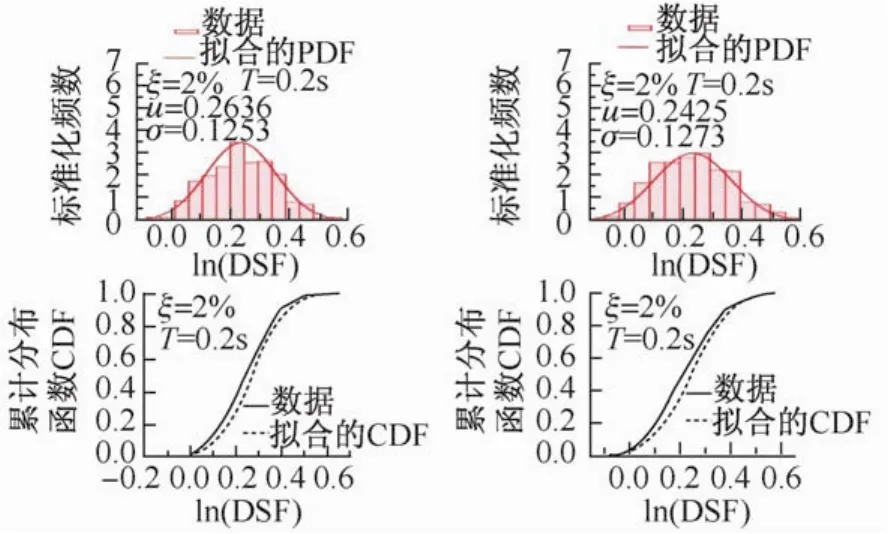
图5 ln（DSF）的分布和拟合曲线Fig.5 Distribution of ln（DSF）and fitted curve

5 建立回归模型

5.1 回归方程μ（ξ，T，Mw）

首先设回归方程仅是ξ和T的函数，取回归模型为

在指定周期Ti和阻尼比ξj处，μ（ξj，Ti）的估计值为

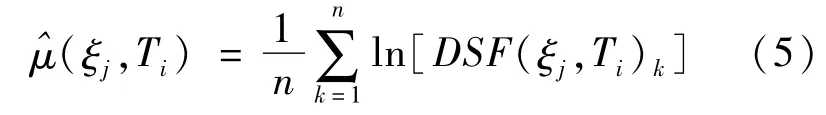
其中，ln［DSF（ξj，Ti）k］为在Ti和ξj处ln（DSF）的第k个数据值，n＝408为数据总数；在Ti和ξj处，第k个数据与回归方程的残差［Δ（ξj，Ti）］k为

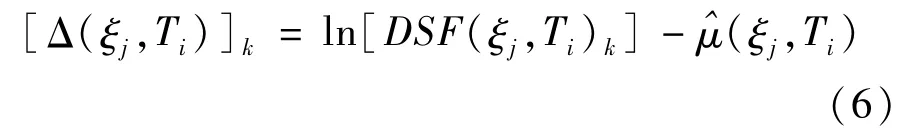
按式（6）可求出在ξj和Ti处每个数据与回归方程的残差，然后可作出残差相对于Mw和D5-95的分布。图6和图7给出了在T＝0.1 s和3 s处，ξ＝2%和20%时，残差相对于Mw和D5-95的分布。分别将计算出的残差按Mw和ln（D5-95）各分为9组。按Mw分组的情况为：5≤Mw＜5.3、5.3≤Mw＜5.6、5.6≤Mw＜5.9、5.9≤Mw＜6.2、6.2≤Mw＜6.5、6.5≤Mw＜6.8、6.8≤Mw＜7.1、7.1≤Mw＜7.4和Mw≥7.4。

按ln（D5-95）分组的情况为ln（D5-95）＜1.7、1.7＜ln（D5-95）＜2、2＜ln（D5-95）＜2.3、2.3＜ln（D5-95）＜2.6、2.6＜ln（D5-95）＜2.9、2.9＜ln（D5-95）＜3.2、3.2＜ln（D5-95）＜3.5、3.5＜ln（D5-95）＜3.8和ln（D5-95）＞3.8。

图中黑色方框代表每组残差的均值，黑线为均值的连线，表明了残差随Mw和D5-95的分布。根据残差分析可知：在短周期处（如T＝0.1 s），各阻尼比下的残差基本随机对称的分布于零水平线的两侧（见图6和图7），这表明了在短周期处Mw及D5-95对DSF没有显著的影响；在长周期处（如：T＝3 s），各阻尼比下的残差相对于Mw近似显直线分布，相对于D5-95显曲线分布，这表明了在长周期处Mw及D5-95对DSF有显著的影响。以上通过残差分析所反映的Mw对DSF的影响是与前文的分析结果是相一致的。

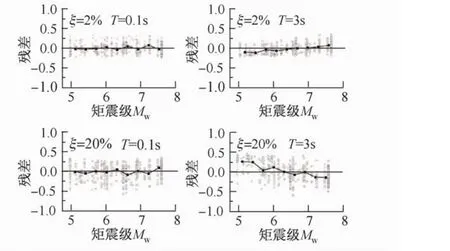
图6 残差相对于Mw的分布Fig.6 Residuals vs.Mw

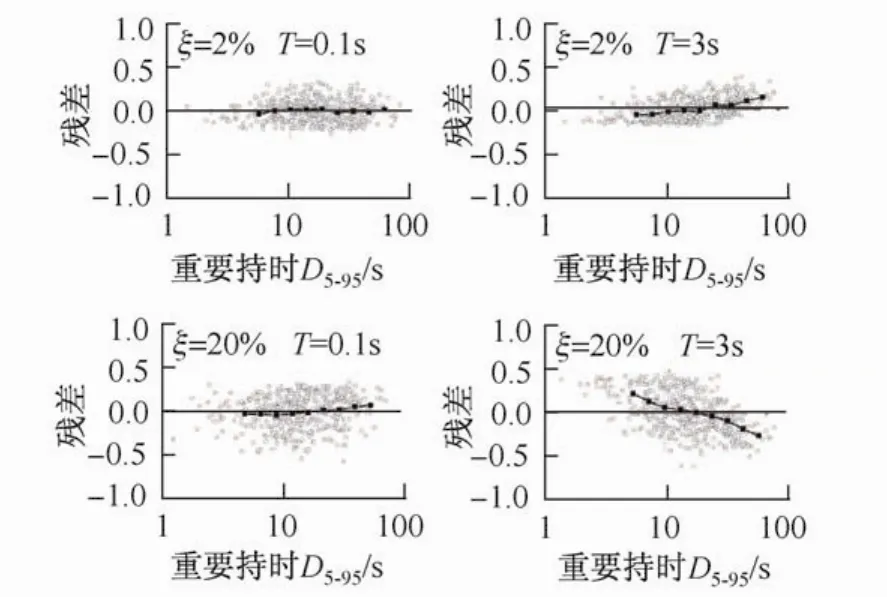
图7 残差相对于D5-95的分布Fig.7 Residuals vs.D5-95

为了改善长周期处残差相对于Mw的分布，在指定周期点Ti处，本文将回归方程取为Mw的线性函数：

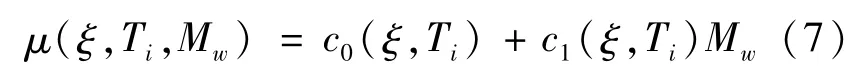
在指定周期点Ti处，回归过程分为以下两步。

第一步：在Ti处，用最小二乘法回归出式（7）中在指定阻尼比ξj处，主系数的估计值（＾c0（ξj，Ti）和＾c1（ξj，Ti））。

对11个阻尼比重复上述过程，可获得所有阻尼比处主系数的估计值。

第二步：在Ti处，采用y＝a＋b lnξ＋c（lnξ）2的函数形式来拟合主系数的估计值与ξ之间的关系（ξ取为百分号中的数值，例如，当阻尼比为5%时，取ξ＝5，以下各方程中均类同）。设

以11个阻尼比处主系数的估计值为数据点，分别对式（8）和式（9）执行回归分析，可求得式（8）和式（9）中次系数的估计值（如＾b0（Ti）、＾b1（Ti）和＾b2（Ti）等）。图8给出了在T＝0.1 s和3 s处，式（8）和式（9）的拟合结果。对20个周期点重复上述回归过程，可获得所有周期点处的回归方程。在Ti处的回归方程如下式：

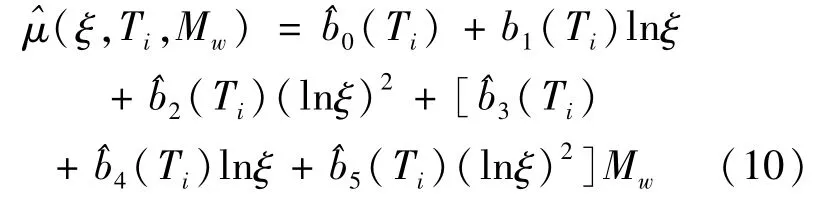
表2给出了20个周期点处回归系数的估计值。其余周期点处回归系数的估计值可由线性插值确定。在Ti和ξj处，第k个数据与回归方程的残差为：

按式（11）求出在ξj和Ti处每个数据与回归方程的残差，然后可作出残差相对于Mw和D5-95的分布。图9和图10给出了在T＝0.1 s和3 s处，ξ＝2%和20%时，残差相对于Mw和D5-95的分布。根据残差分析可知：在短周期处（如T＝0.1 s），采用式（11）的回归方程对残差相对于Mw和D5-95的分布无明显影响（将图6、图7与图9、图10对比可知），再次说明在短周期处Mw和D5-95对DSF无显著影响，各阻尼比的残差随机对称的分布于零水平线的两侧；在长周期处（如T＝3 s），采用式（10）的回归方程使得残差相对于Mw不再具有直线分布，各阻尼比下的残差随机对称的分布于零水平线的两侧（见图9），这说明了本文回归模型的合理性且能反映出长周期处Mw对DSF的影响；此外，采用式（10）的回归方程极大地改善了长周期处残差相对于D5-95的分布（对比图7和图10），间接地反映了D5-95对DSF的影响。图11给出了在ξ＝0.5%、2%、7%、15%和25%处，按本文模型（取Mw＝6.5）所计算的DSF中值与本文数据（Mw＝6～7）所计算的DSF中值的对比。由图可见，两者吻合得较好。

现以一算例进一步说明所建议模型的有效性及模型中考虑矩震级影响的必要性。对于基地隔震结构，当上部结构的抗侧刚度远大于隔震层的抗侧刚度时，可将其简化为一单自由度体系。设有一基地隔震结构，上部结构的抗侧刚度远大于隔震层的抗侧刚度，基本周期为3 s，阻尼比为30%。该结构可简化为自振周期为3 s，阻尼比为30%的单自由度体系。当该体系遭受表1中矩震级Mw＝7～8的地面运动记录激励时，通过分析可求得该体系精确的阻尼调整系数中值为0.488（图3）。对式（5）取指数，可求得不考虑矩震级影响的阻尼调整系数模型的阻尼调整系数中值为0.579。取Mw＝7.5，采用本文所建议的考虑矩震级影响的阻尼调整系数模型所求得的阻尼调整系数中值为0.48。由上述计算可见：采用不考虑矩震级影响的阻尼调整系数模型计算的阻尼调整系数中值所产生的误差为＋18.6%（“＋”代表高估）；采用本文建议的考虑矩震级影响的阻尼调整系数模型计算的阻尼调整系数中值所产生的误差仅为－1.6%（“－”代表低估），在工程允许的误差范围内。以上分析说明了考虑矩震级对阻尼调整系数影响的必要性，尤其对于长周期大阻尼比的结构，不考虑矩震级的影响将带来较大的误差，也说明了本文模型的有效性和优越性。

图8 ＾c0，＾c1和拟合曲线Fig.8 ＾c0，＾c1and fitted curve

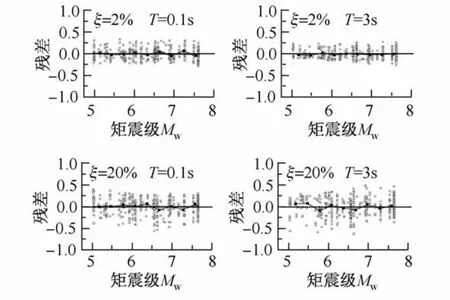
图9 残差相对于Mw的分布Fig.9 Residuals vs.Mw

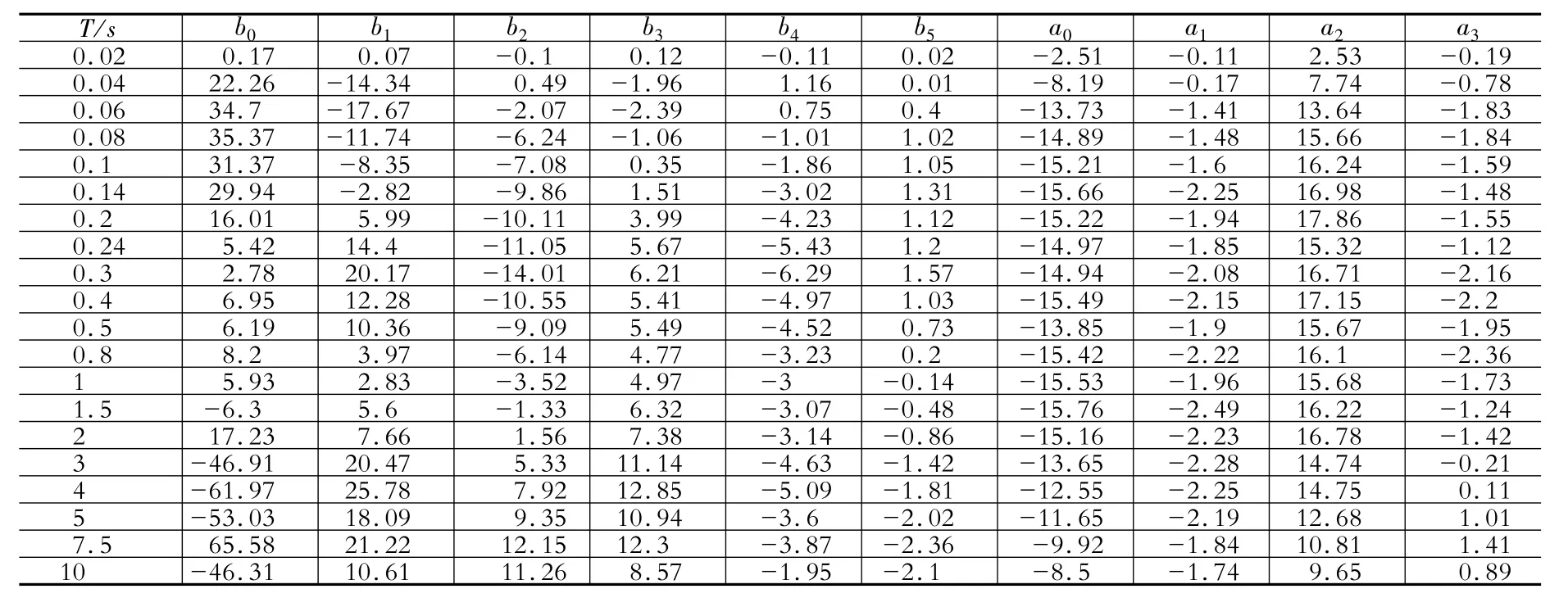
表2 模型回归系数（×10-2）Table 2 Regression coefficients for themodel（×10-2）

图10 残差相对于D5-95的分布Fig.10 Residuals vs.D5-95

图11 本文模型和数据的DSF中值对比Fig.11 Comparison on median DSF between the model and data

5.2 标准差σln（DSF）

对于一元线性方程，在Ti和ξj处，＾σlnDSF（ξj，Ti）的无偏估计可用下式［18］计算：在指定的Ti处，用式（12）可求得11个阻尼比处

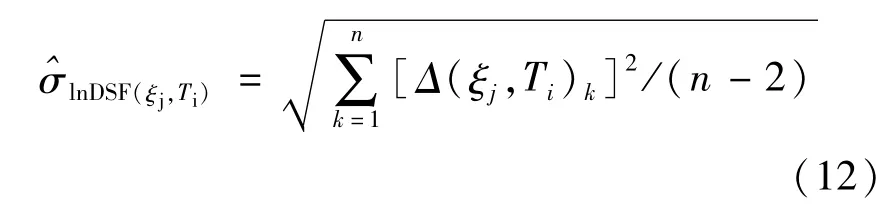
标准差的估计值。在Ti处，本文采用的函数形式来拟合标准差的估计值与ξ之间的关系。取：

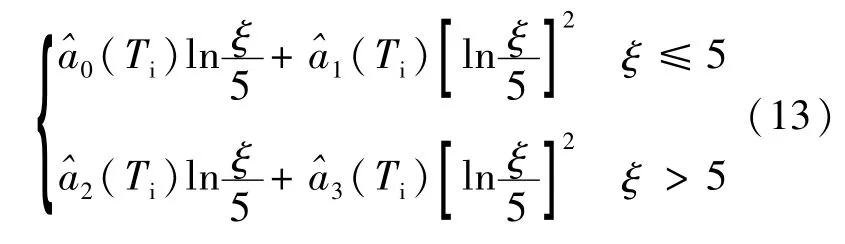
图12给出了在T＝0.1 s和3 s处式（13）的拟合结果。由图可见，DSF相对于ξ存在异方差性。随着ξ越远离5%，DSF的离散程度越大。这与前文的分析结果是一致的。各周期点处回归系数的估计值列于表2。

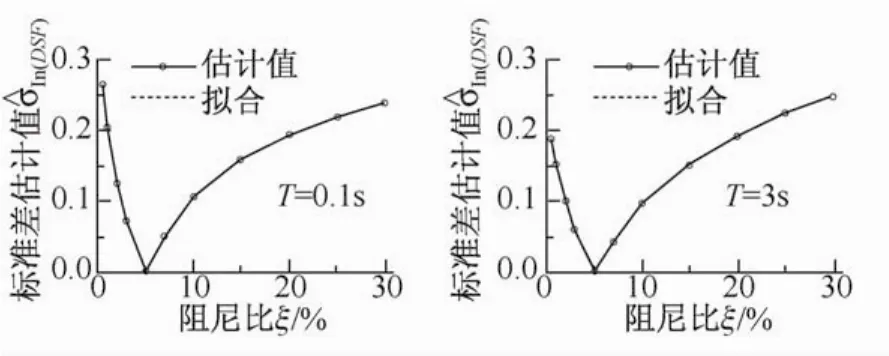
图12 ＾σln（DSF）和拟合曲线Fig.12 ＾σln（DSF）and fitted curve

6 结 论

基于408条地震地面运动记录，本文研究了Mw对DSF的影响，并在此基础上提出了考虑Mw影响的回归模型，得出以下结论：

（1）Mw对DSF的影响与T和ξ有关；在T＞0.6 s的范围内，当ξ＜5%时，DSF随着Mw的增长而增长；当ξ＞5%时，DSF随着Mw的增长而减小。随着T的增长，Mw对DSF的影响越显著；ξ越远离5%，Mw对DSF的影响越显著。在T＜0.6 s的范围内，Mw对DSF无显著影响；

（2）当Mw＝5～6时，DSF受T的影响显著；随着Mw的增大，在T＞0.6 s范围内，DSF受T的影响逐渐减弱；当Mw＝7～8时，除ξ＝0.5%和1%外，在T＞0.6 s范围内，DSF基本不随T而变化。

（3）DSF相对于ξ存在异方差性；ξ越远离5%，DSF的离散程度越大。

（4）本文所提出的回归模型能体现Mw对DSF的影响，及DSF相对于ξ的异方差性，也能间接地体现D5-95对DSF的影响。

［1］ 中华人民共和国住房和城乡建设部.GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.Ministry of Housing and Urban-Rural Department of the People’s Republic of China.GB 50011—2010 Code for seismic design of buildings［S］.Beijing：China Architecture and Building Press，2010.（in Chinese）

［2］ UBC.Uniform building code［S］.Whittier，CA：International Conference of Building Officials，1994，1997.

［3］ IBC.International building code［S］.Whittier，CA：International Conference of Building Officials，2000.

［4］ NEHRP.Recommended provisions for seismic regulations for new buildings［R］.Washington，DC：Federal Emergency Management Agency，1994，1997，2000.

［5］ FEMA-273.NEHRPGuidelines for the seismic rehabilitation of buildings［R］.Washington，DC：Federal Emergency Management Agency，1997.

［6］ Eurocode 8.Design of structures for earthquake resistance，part 1：general rules，seismic actions and rules for buildings［S］.Brussels：European Committee for Standardization，2004.

［7］ Ashour SA.Elastic seismic response of buildingswith supplemental damping［D］.Ann Arbor：University of Michigan，1987.

［8］ Tolis SV，Faccioli E.Displacement design spectra［J］.Journal of Structural Engineering，1999，3（1）：107-125.

［9］ Priestley M.Myths and fallacies in earthquake engineering，revisited［M］.Pavia（Italy）：IUSS Press，2003.

［10］ Newmark N M，Hall W J.Earthquake spectra and design［M］.Oakland：Earthquake Engineering Research Institute，1982.

［11］ Wu J，Hanson R D.Study of inelastic spectra with high damping［J］.Journal of Structural Engineering，1989，115（6）：1412-1431.

［12］ Idriss IM.Procedures for selecting earthquake ground motions at rock sites［R］.Report NISTGCR 93-625，Washington，D.E：National Institute of Standards and Technology，1993.

［13］ Lin Y Y，Chang K C.Effects of site class on damping reduction factors［J］.Journal of Structural Engineering，2004，130（11）：1667-1675.

［14］ Bommer J J，Mendis R.Scaling of spectral displacement ordinates with damping ratios［J］.Earthquake Engineering and Structural Dynamics，2005，34（2）：145-165.

［15］ Cameron W I，Green I.Damping correction factors for horizontal ground-motion response spectra［J］.Bulletin of the Seismological Society of America，2007，97（3）：934-960.

［16］ Kempton J J，Stewart J P.Prediction equations for significant duration ofearthquake groundmotions considering site and near-source effects［J］，Earthquake Spectra，2006，22（4）：985-1013.

［17］ 谢礼立，张晓志.地震动记录持时和工程持时［J］.地震工程与工程振动，1988，8（1）：31-38.Xie Lili，Zhang Xiaozhi.Accelerogram-based duration and engineering duration of ground motion［J］.Earthquake Engineering and Engineering Vibration.1988，8（1）：31-38.（in Chinese）

［18］ Ang A H S，TangW H.Probability concepts in engineering planning and design volume1 basic principles［M］.New York：John Wily and Sons，Inc，1975.

Damping Scaling Factor w ith a Consideration of Influence of M oment M agnitude

WANG Guotao*HU Kexu LEIMin
（Resecnch Institute of Struetural Engineering and Disaster Reduction，Tongji University，Shanghai200092，China）

The influence ofmomentmagnitude（Mw）on damping scaling factor（DSF）was firstly investigated based on the statistical analysis of408 earthquake ground motion records.It is showed that the effect of Mwon DSF depends on period of vibration（T）and damping ratio（ξ）.The DSF increases as Mwincreases for the periods greater than about0.6 s ifξ＜5%，but it decreases ifξ＞5%.The pattern with Mwismuchmore significant as T increases orξdeviates from 5%.Almostno pattern with Mwis seen for the periods less than about 0.6 s.DSF is significantly affected by T when Mw＝5～6.The influence of T on DSF becomes less significant with the increase of Mwfor the periods greater than about 0.6 s.When Mw＝7～8 DSF does not basically change with T within the range of periods greater than 0.6 s except DSF corresponding to 0.5%and 1% damping.The heteroscedasticity in the DSF with respect toξexists.Then DSF regression equation was proposed that only depends on T andξand equation residualswas calculated at specified T andξ.Finally according to the residual plots showing an almost linear relationship with Mwat long periods，the regressionmodel that includes a linearmagnitude term was proposed and regression coefficients were tabulated.Residual analysis shows that the proposed model can reflect the influence of Mwon DSF and can indirectly reflect the influence of significant duration（D5-95）on DSF.The standard deviation of themodel can reflect heteroscedasticity in the DSF with respect toξ.

2013-06-17

国家科技支撑计划重点项目（2009BAJ28B02）*联系作者，Email：802212wgt＠tongji.edu.cn