组合梁桥截面温度分布影响因素对比分析

张凯龙 马如进 陈艾荣

（同济大学桥梁工程系，上海200092）

组合梁桥截面温度分布影响因素对比分析

张凯龙*马如进 陈艾荣

（同济大学桥梁工程系，上海200092）

针对某变形精确控制组合梁桥的温度变形问题，综合桥梁所处地理环境特征、桥梁结构几何构型等因素，实现对相关随机气象参数（尤其太阳辐射强度）的取值修正；进而通过对结构热环境的有限元模拟，得到截面温度分布的数值结果。以此为基础，着重探讨了三种结构材料（沥青混凝土、混凝土和钢）的相关热力学参数以及沥青混凝土铺装层厚度对截面温度分布的影响方式及程度，并就对应的荷载效应进行了定性的评估与对比。以此为指导，结合目前新型材料的优良热力学性能，工程人员可采取针对性设计或补偿措施达到降低梁体温度变形响应及优化线形的目的。

组合梁桥，温度分布，对流换热，时程模型，参数分析

1 引 言

自20世纪50年代，桥梁结构的温度变化被归结为三方面：日照温度作用、骤然降温作用和年温温度变化等［1］。其中，尤以日照温度作用产生的问题最为复杂，其核心在于提出特定地理特征条件下的截面温度梯度模型。比较有代表性的是由Kennedy和Soliman于1987年提出的双折线模型，如图1所示［2］。

图1 组合梁桥双折线温度梯度模型Fig.1 The temperature gradientmodel of the composite bridge

目前，欧洲规范采用了非线性双折线分布模式的正常算法和简化算法［3］。而美国AASHTO规范和我国的公路桥梁设计规范采用了相似的非线性双折线梯度模型［4，5］。而我国现有的《钢结构设计规范》中尚未给出相应的计算方法［6］。

但上述模型在工程实践中却暴露出诸多涉及使用性能的问题，尤其在一些变形精确控制桥梁（高铁桥梁、磁悬浮桥梁等）上体现得更明显。

以高铁桥梁为例，目前在欧洲不少高铁线路的建设中，组合梁桥受到青睐。但在线路投入运行后，通过检测，发现某些地区多跨连续组合梁桥的边跨段，在夏季出现了预期外的具有日循环周期特征的非正常变形。这一变形显著影响着轨道的平顺性，从而进一步威胁着高速列车的行车舒适度和相关材料的耐久性。通过初步分析，研究人员推断这一变形的根源是温度作用。

目前，既有规范所强调的仅是最不利温差分布情形下的一种状态分析，而针对一些敏感度较高的结构，尚存在以下几个问题：

（1）对不同桥梁结构的几何特征（梁体方位、截面构造等）未加区分；

（2）对地理特征和气象条件的考虑较粗糙；

（3）对结构所采用材料的热力学参数的特殊性及相关随机影响因素未予考虑。

因此，本文以某公路组合梁桥为例，首先结合桥梁几何特征及日照情况，明确日照影响的范围和程度；然后建立有限元模型，着重分析各参数对截面温度分布的不同影响。这一分析将有助于研究人员明确温度作用的机理，并为后续针对既有问题桥梁的工程补偿措施的提出提供参考。

2 温度时程分析基本原理

根据传热学原理，热量传递有三种基本方式：热传导、热对流和热辐射［7］。日照条件下组合梁桥与周围环境的热交换情况如图2所示。

图2 组合梁桥结构与环境热交换过程Fig.2 Thermal interaction between a structure and environment

在各种环境因素的作用下形成的这一温度场实质是一个三维非稳态温度场，为简化计算，可忽略构件纵向的温度梯度，按平面问题计算温度场［8，9］，然后用二维热传导方程表示，再加上适当的边界条件和初始条件即可求解。相关方法在文献［10］中已有较详细的阐述。在此基础上，借助有限元软件，可以进行组合结构温度场的瞬态分析，得到温度场随时间的变化规律。

3 气象参数及材料参数

为提高温度场时程分析的可靠性，必须考虑太阳辐射、气温和风速等气象参数的随机性。由于本文着重探讨各参数的影响方式和程度，其随机分布规律［10］不在探讨范围，故以下分析将以既有气象数据资料为基础。

3.1 太阳辐射量的时程处理方法

太阳辐射作用是一个由多因素共同影响的过程，其主要涉及以下四个因素：

（1）桥梁地理位置及其方位角；

（2）太阳的位置：高度角和方位角；

（3）桥梁结构各截面的几何特征；

（4）太阳辐射量的时程特征。

针对前两个因素，传统的分析方法需要通过计算赤纬角、太阳时角等天文学参数，结合目标经纬度计算某一给定时刻的太阳方位角、高度角等参数。这一方法计算过程复杂，易出错，下面推荐另一种更为准确、实用的计算工具。

SunEarthTools是一款太阳能领域研究专用的在线应用计算工具。输入地球上任意位置的地理信息（城市名或经纬度）及时间，即可得到当日目标位置处的太阳运行轨迹（如图3以上海为例）以及每隔10 min的太阳方位角和高度角数据，并可以直接输出为Excel表格形式。大大方便后续的分析工作。

结合太阳和结构的各几何参数，通过立体几何关系即可计算和判断每个边界在一天当中受太阳直射的时间区段，这样区别分析有助于准确模拟结构所处的热环境。这一几何分析过程容易理解，但Excel计算内容琐碎，这里不做展开，仅在表2中示以结果。

3.2 材料参数的取值

材料（包括结构材料和附属材料）特性对热交换过程的影响是目前研究的热点，其核心就是明确不同材料参数对热量传递过程的影响方式和程度并寻找关键因素。这也是下文分析的重点。

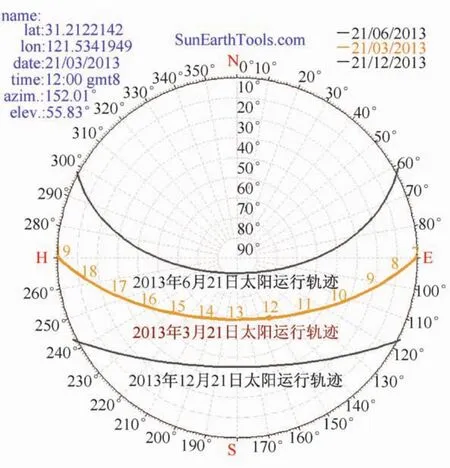
图3 上海市2013年3月21日，6月21日及9月21日的太阳运行轨迹（来源：SunEarthTools.com）Fig.3 Daily sun path in Shanghai on 21／3／2013，21／6／2013 and 21／9／2013（Source：SunEarthTools.com）

4 算例分析

4.1 桥梁概况

一座六跨连续组合梁公路桥，跨度组合为47.3 m＋4×60 m＋47.3 m，如图4所示。大桥为双向六车道，分为独立的两幅。大桥的走向为南偏西10°。大桥采用传统的双梁式钢板组合梁结构，其中边跨跨中截面尺寸如图5所示。这里忽略截面横坡以简化分析。

图4 组合梁桥桥跨布置图（单位：mm）Fig.4 Arrangement of the bridge spans（Unit：mm）

经搜集，表1列举了所涉及材料的主要类别及参数初值（具体定义将在下文逐一解释）。因以下分析将会通过变化参数取值来评估其效应，故参数初值的偏差并不影响分析的结论。相关参数初值的确定过程可参考文献［11，12］。

图5 边跨跨中截面构造及尺寸（单位：mm）Fig.5 Cross section of in themiddle of the side span（Unit：mm）

表1 材料热力学参数及其初值Table 1 Thermodynam ic parameters and their initial values of differentmaterials

4.2 有限元模型

采用ANSYS Mechanical进行温度场的瞬态分析。以边跨跨中截面为对象，此处钢梁壁板最薄，温度效应也最为显著。模型采用热传导平面单元PLANE55和界面单元SURF151，见图6。

图6 温度时程分析有限元模型Fig.6 Finite elementmodel for the temperature-time analysis

建模中除须设定加载的对象和顺序外，还要注意一个问题，即ANSYS中同时施加对流面荷载和热流密度的不可叠加性，对此，通过一定的编程技巧可以予以解决。此外，模型取5日中的第1日清晨6h30的环境温度值15℃作为分析的初始值。

本算例的荷载主要包括两部分：一是环境温度值（对流面荷载）；二是太阳辐射值（热流密度）。这里不采取人为计算［10］而是现成气象数据，因两种途径的差别并不影响最终结论。由The Solar Data Warehouse获取美国棕榈谷（Palmdale）地区2005年6月间的完整气象记录，取26日至30日这5天，从中提取每半小时的环境温度和太阳辐射值数据，施加于相应单元和边界上。另外，对于结构下表面，还应考虑地面反射太阳光的辐射作用，这一辐射量一般取太阳辐射量的0.2倍（裸露岩土）或0.25倍（植被覆盖）［13］，本文取前者。

根据3.1中方法计算得到截面各个边界每日受太阳辐射的时间范围，这里列出26日的分析结果，如表2所示。以此为依据，对不同边界上施加的热流密度荷载进行相应的处理即可。

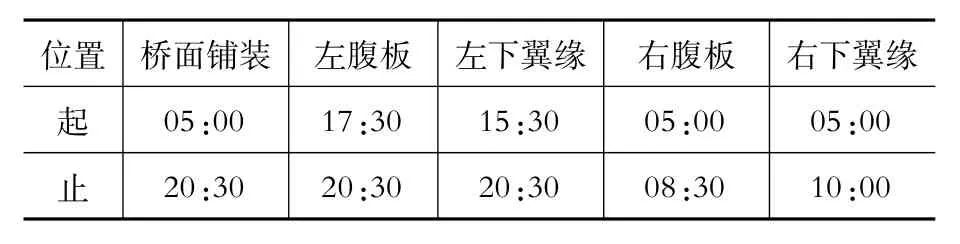
表2 组合梁截面各边界在6月26日受太阳辐射的时间范围Table 2 Time range for different edges of the section under the sun in 26／06／2005

4.3 计算结果分析

截面内温度分布随时间的变化过程是分析的重点。选取10个具有代表性的节点，绘制其温度时程曲线。然后通过规律地改变特定参数的取值来对比同一节点处温度时程曲线的变化情况，进而得出对参数的评估结论。这10个代表性的节点分布如图7所示。

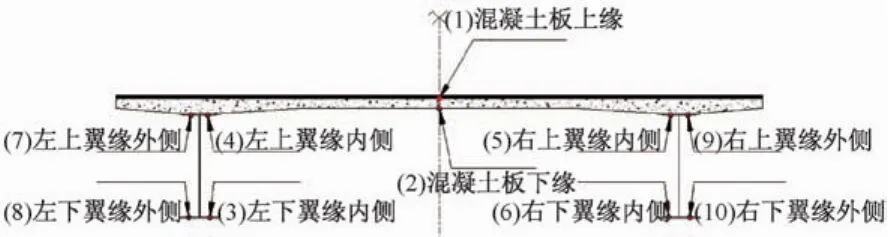
图7 10个代表性节点Fig.7 Ten representative nodes

初始值下各代表性节点处温度的时程变化曲线如图8、图9所示。

根据曲线走势，可主要归纳出以下两方面结论：

（1）内外不均：表现为内部空间温度变化相对滞后，从而形成内外温差，引起温差变形响应。

图8 初始值下截面不同位置处温度时程曲线（1）Fig.8 Temperature-time curves in different positions of the section with initial parameter values（1）

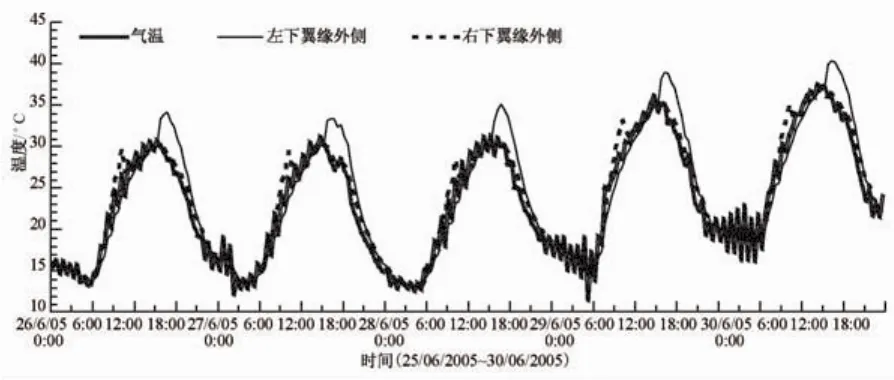
图9 初始值下截面不同位置处温度时程曲线（2）Fig.9 Temperature-time curves in different positions of the section with initial parameter values（2）

（2）左右不均：太阳辐射的方向性和时段性引起左右温差，进而形成水平向的温差变形响应。

这些截面温度分布的基本特点揭示出下文参数分析的主要目标：探讨引发截面温度分布不均衡的关键因素，进而为补偿措施的提出做参考。

4.3.1对流换热系数（h）的影响

这里对流换热系数包含了两方面含义：对流换热（hc）和热辐射散热（hs）。这两者中的前者受风速（v，m／s）影响最为明显，Kehlbeck［12］提出的换算关系式为

而hs受热辐射率（ε）的影响较显著，即取决于材料的特性以及介质温度。其换算关系同样在文献［12］中有阐述。这两者之和的取值以表1为准。

因此，基于对结构内外气流差异影响的考虑，将参数分为两类：h外和h内，并通过逐步变化取值的倍数（0.5，1，1.5和2.0）计算截面不同位置处的温度变化情况。

1）外部对流换热系数：h外

经分析，混凝土板受该系数的影响最为显著，且取值越小，混凝土板上缘的温度越高。

这是由于该系数取值的大小对应于构件与外界环境热交换的强弱，值越小，交换程度也越弱，从而蓄积的热量也越难散去。

同样的影响也出现在钢梁内，如图11、图12所示。系数越大，热交换的程度越高，从而构件的温度变化幅度也越接近环境温度的变化幅度。

图10 外部对流换热系数（h外）对砼桥面板上缘的影响Fig.10 Influence of the outside convective heat transfer coefficient on the top border of the concrete deck

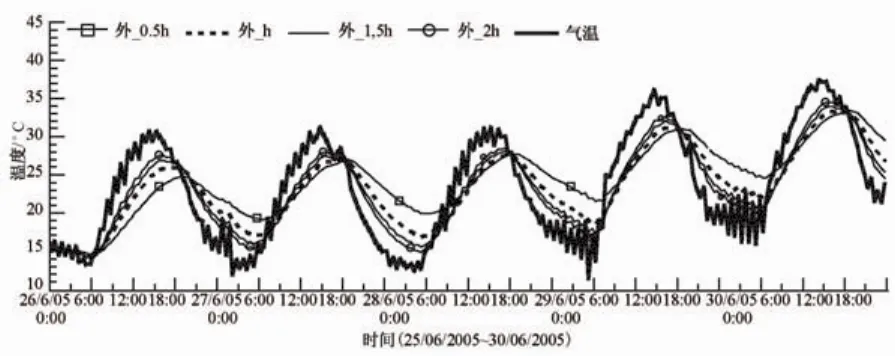
图11 外部对流换热系数（h外）对左上翼缘外侧的影响Fig.11 Influence of the outside convective heat transfer coefficient on the outside part of the left top flange

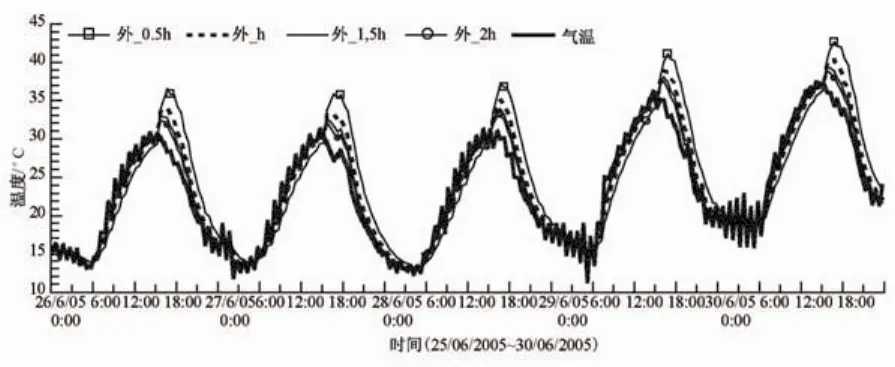
图12 外部对流换热系数（h外）对左下翼缘外侧的影响Fig.12 Influence of the outside convective heat transfer coefficient on the outside part of the left bottom flange

2）内部对流换热系数：h内

内部对流换热系数（h内）对截面各部分的影响较弱，但本质规律不变。

综上所述，对流换热系数这一参数直接影响着结构内、外区域之间的温差。这一温差过大，易造成薄壁型截面的畸变，引发温度变形响应。因此，设计中宜通过合理的布置（如结构通透）来尽量实现温度分布的均匀、合理。

4.3.2表面太阳辐射吸收系数（α）的影响

太阳辐射吸收系数（α）是材料表面吸收的太阳辐射量值与入射的总太阳辐射量值的比值。这一参数的取值取决于材料表面的颜色以及材质。这里在初始值0.9的基础上，分别对桥面铺装和钢梁依次取值0.7，0.5和0.3，分析其温度时程分布曲线，结果如下。

1）桥面太阳辐射吸收系数：α桥面

由图13可见，随着α桥面线性减小，混凝土板内的温度也线性减小，且系数每变化0.2所引起的温度变化量级在1℃～2℃。

图13 桥面太阳辐射吸收系数（α桥面）对砼桥面板上缘的影响Fig.13 Influence of the solar radiation absorbility factor of the bridge floor on the top border of the concrete deck

2）钢梁太阳辐射吸收系数：α钢

图14 钢太阳辐射吸收系数（α钢）对左下翼缘外侧的影响Fig.14 Influence of the solar radiation absorbility factor of the bridge floor on the outside part of the left bottom flange

综合上述分析可见，与h相比，α对截面温度分布的影响更为显著，对结构温度变形响应的影响也更为直接。降低桥面太阳辐射吸收量有助于减小竖向温差，从而有效削弱竖向的温度变形响应；而降低钢梁的太阳辐射吸收系数不仅有前述效果，同时还可有效减小截面左、右温度分布的不均及相应水平向的温度变形响应。

4.3.3热导率（λ）的影响

λ是材料固有的热力学属性，取值主要受到材料属性、环境温度、湿度及气压的影响。

这里针对三种材料，逐步变化各自λ取值的倍数（0.5，1，1.5和2.0），然后计算比较截面不同位置处的温度变化情况。

1）桥面铺装层热导率：λ铺装

λ铺装对混凝土板的温度影响最显著、直接。由图15可见，随着λ线性增大，混凝土板内的温度呈非线性增长，即影响程度越来越弱。这是由于取值的升高，导致热量的获取快于热量的扩散，从而温度波动的幅值增大。

图15 铺装层热导率（λ铺）对混凝土桥面板上缘的影响Fig.15 Influence of the thermal conductivity of the pavement on the top border of the concrete deck

2）钢梁热导率：λ钢

对于钢梁来说，λ的升高同样造成梁体板件内温度波动幅度的加大，但其影响并不如λ铺装的影响来得明显。

3）混凝土桥面板热导率：λ砼

从以上表格我们可以总结出：将“小”与“少”误用的情况所占比例为一半以上，是本文的重点研究对象，其次是将动词“减少”与“少”误用，占到10%左右，剩下还有21种与“少”误用的情况，我们将分析其中比较有代表性的“消失”、“多”与“不多”，同时也可以发现与“少”误用的词语大部分是表示“减少”的词语，仅有几例表示“增加”。

由图16和图17可见，λ砼与λ铺装的影响方式有所不同。随着λ砼的增大，混凝土板上缘的温度波动幅度非线性减小，而下缘却在非线性增大。且参数取值越小，其温度波动相对于环境温度波动的滞后程度越明显。

图16 混凝土桥面板热导率（λ砼）对自身上缘的影响Fig.16 Influence of the thermal conductivity of the concrete deck on the top border of itself

图17 混凝土桥面板热导率（λ砼）对自身下缘的影响Fig.17 Influence of the thermal conductivity of the concrete deck on the bottom border of itself

这一现象的原因在于，随着λ砼的增大，混凝土板整体的温度分布趋向于均匀，趋于有利。

由以上分析可见，λ一方面影响热量的吸收量（铺装），另一方面显著影响着温度在截面内分布的均匀性。吸收量过大且传导不畅会加剧竖向温差，增大竖向温度变形响应。因此，选材时须依据以上分析结论进行合理配置。

4.3.4比热容（c）的影响

同热导率一样，比热容也是材料固有的一种属性。比热容的变化主要受温差及物质状态等的影响。经同样的分析过程发现，随着c的增大，混凝土板内的温度波动幅度在减小。但应注意到，这一参数的影响并不明显，非控制因素。

4.3.5桥面铺装层厚度的影响

由前述分析可见，桥面铺装层的热力学性能在截面温度分布变化中扮演着重要角色。对于一般公路桥梁的铺装层而言，相比于改变其材料的固有参数，改变厚度是一种更为可行的方式。因此，在以下分析中铺装层厚度将从5 cm逐级增加至12.5 cm，每一级增幅设为2.5 cm，然后分别计算绘制其温度时程曲线进行对比分析。

由图18可见，厚度较小时，每增加2.5 cm，波动幅度减小2℃～3℃。当铺装层厚度超过10 cm，其对温度波动的影响逐渐减弱，可以预见，当厚度超过15 cm，其影响已基本可忽略。

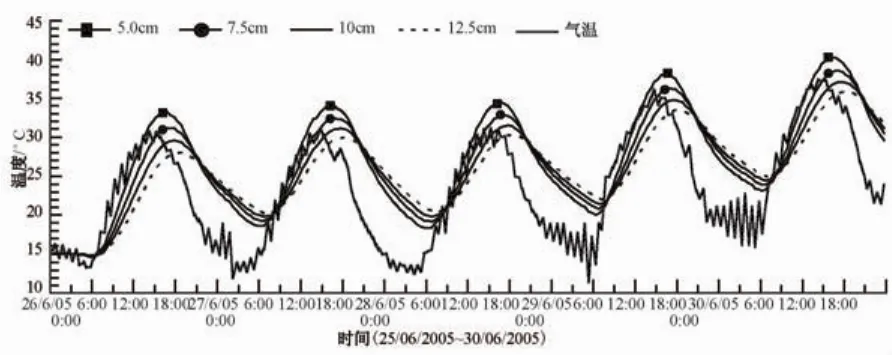
图18 桥面铺装层厚度对砼桥面板上缘的影响Fig.18 Influence of the thickness of the pavement on the top border of the concrete deck

由此可见，桥面结构设计时，在满足行车性能的前提下，应尽量避免采用过薄的铺装层，可以通过适当增加铺装的厚度（以10～12.5 cm为宜）来改善结构的温度分布状况，从而减小温度变形响应。

5 结论和展望

通过上述分析，所得结论总体归纳如下：

（1）外部对流换热系数（h外）越大，截面的温度峰值越小，但其影响程度随着该参数取值的增大而减弱。

（2）表面太阳辐射吸收系数（α）与截面温度变化幅度呈线性正相关，影响直接而显著。

（3）铺装层热导率（λ铺）和混凝土板热导率（λ砼）对截面温度分布的影响是不同的，前者增大会加剧温差效应，而后者增大则削弱温差效应。

（4）比热容（c）和铺装层厚度的影响较类似，随参数取值增大，影响程度减弱。但二者不同的是，前者是材料的固有参数，不易改变，而后者属于设计可控范围，可以通过设计实现取值的优化。

截面温度分布是结构温度变形响应的直接影响因素，明确了前者的分布规律，有助于工程人员采取针对性的措施来平衡乃至消除截面内温度分布的这种不均衡，进而减小相应的温差变形。

目前，具备优良热力学性能的各类新型材料不断涌现，为降低修缮成本，通过附加保护措施来实现对既有结构温度变形的补偿已成为可能。因此，若能依照上述结论寻找到合适的材料，借助合理的设计方法，就能够达到降低梁体温度响应位移，优化线形的目的，从而更有效地满足结构的可靠性和耐久性需求。

［1］ 陈璨.钢板组合梁桥的温度及温度效应研究［D］.长沙：中南大学，2012.Chen Jie.Study on the temperature field and its action on steel plate-girder bridges［D］.Changsha：Zhongnan University，2012.（in Chinese）

［2］ Kennedy JB，Soliman M H.Temperature distribution in composite bridges［J］.ASCE-J Struct Eng，1987，113（3）：475-82.

［3］ CEN：European Committee for Standardization，BSI：British Standards Institution.EUROCODE（English Version）［S］.BSI，1990-2010.

［4］ U.S.Department of Transportation.AASHTO，Load and resistance factor design，bridge design specifications［S］.1994.

［5］ 中华人民共和国交通部.JTG D60—2004公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.Ministry of Communications of the People′s Republic of China.JTG D60—2004 general code for design of highway bridges and culverts［S］.Beijing：China Communications Press，2004.（in Chinese）

［6］ 吴迅，陈经伟，肖春，等.温差、收缩引起的钢-混凝土组合梁界面处剪力作用研究［J］.结构工程师，2009，25（1）：41-44，54.Wu Xun，Chen Jingwei，Xiao Chun，et al.Study on shear effect caused by temperature and shrinkage on the interface of steel-concrete composite beams［J］.Structural Engineers，2009，25（1）：41-44，54.（in Chinese）

［7］ 刘兴法.混凝土结构的温度应力分析［M］.北京：人民交通出版社，1999.Liu Xingfa.Analysis of temperature stress of concrete structure［M］.Beijing：China Communications Press，1999.（in Chinese）

［8］ Mirambell E，Aguado A.Temperature and stress distributions in concrete box girder bridges［J］.Journal of Structural Engineering，1990，116（9）：2388-2409.

［9］ Saetta A，Scotta R，Vitaliani R.Stress analysis of concrete structures subjected to variable thermal loads［J］.Journal of Structural Engineering，1995，121（3）：446-457.

［10］ 肖建庄，宋志文，赵勇，等.基于气象参数的混凝土结构日照温度作用分析［J］.土木工程学报，2010，43（4）：30-36.Xiao Jianzhuang，Song Zhiwen，Zhao Yong，etal.A-nalysis of solar temperature action for concrete structure based on meteorological parameters［J］.China Civil Engineering Journal，2010，43（4）：30-36.（in Chinese）

［11］ 逯彦秋，张肖宁，王圣保.钢箱梁桥沥青混凝土铺装层温度场的模拟分析［J］.沈阳建筑大学学报（自然科学版），2006，22（5）：750-754.Lu Yanqiu，Zhang Xiaoning，Wang Shengbao.Simulation analysis of temperature field of the asphalt concrete pavement of steel box girder bridge［J］.Journal of Shenyang Jianzhu University（Natural Science Edition），2006，22（5）：750-754.（in Chinese）

［12］ 刘兴法（译）.太阳辐射对桥梁结构的影响［M］.北京：中国铁道出版社，1981.Liu Xingfa.The effect of solar radiation on bridge structure［M］.Beijing：China Railway Publishing House，1981.（in Chinese）

［13］ Tayeb Ameziane El Hassani，étienne Persoons.Agronomie moderne：bases physiologiques et agronomiques de la production végétale；ouvrage collectif［M］.Paris：Hatier，1995.

Com parative Study of Influential Factors for Tem perature Distribution in a Composite Bridge Cross-section

ZHANG Kailong*MA Rujin CHEN Ai’rong
（Department of Bridge Engineering，Tongji University，Shanghai20092，China）

This article studied thermal deformation of composite bridges.Firstly，based on geographical location and geometric characteristics of a bridge，themethod to adopt solar radiation datawas corrected.Numerical results of temperature distribution in the cross-section were acquired by finite elementmodeling.Secondly，by numerical calculations，different influential factors such as pavement thickness，various thermodynamic parameters of the three components of the structure，which include asphalt deck pavement，concrete deck and steel beam，were studied.It is concluded that proper thermodynamic properties ofmodern materials can be used to compensate of thermal deformation of a bridge.

composite bridge，temperature distribution，convection，time historymodel，parameter analysis

2013－09－30

*联系作者，Email：kailong.zhang＠hotmail.com