箱形截面扭转刚度的计算方法分析

牛金龙 金志强

（1.上海市城乡建设和交通委员会科学技术委员会，上海200032；2.沈阳远大铝业工程有限公司，沈阳110027）

箱形截面扭转刚度的计算方法分析

牛金龙1，*金志强2

（1.上海市城乡建设和交通委员会科学技术委员会，上海200032；2.沈阳远大铝业工程有限公司，沈阳110027）

在工程应用中，采用箱形截面承受外力偶的作用，在极限状态设计中要对箱形截面的扭转角及扭转剪应力进行校核，但箱形截面的抗扭刚度采用经典的弹性力学解析解比较困难。采用有限元软件ANSYS和弹性力学薄膜比拟计算方法及材料力学简化计算方法分别针对矩形截面及箱形截面的抗扭转刚度进行了分析性对比，并绘出相应的曲线图，相应提出了三种计算方法的使用性范围，同时给出了相同厚度条件下ANSYS及弹性力学解析解计算扭转刚度比值δ随a／b的变化曲线，对工程的应用具有指导性意义。

力偶，箱形截面，抗扭刚度，有限元，薄膜比拟

1 引 言

在幕墙结构及其建筑结构工程应用中，由于结构设计上的要求，使矩形截面构件承受扭转外力偶作用，在对截面进行承载能力极限及使用能力极限要求校核时，要计算截面的剪应力和杆件的扭转角。但矩形截面构件的自由扭转不同于圆柱截面的扭转，由于轴向翘曲变形的存在，使得材料力学［1］方法在解决问题上遇到了很大的困难。针对这些问题，于海洋等［2］利用应力函数法求得的截面剪应力解析解表达式和运用有限元分析得到了关于截面控制线上的剪应力分布规律。尹刚等［3］采用加权残值解法对矩形截面进行的分析。但由于目前的截面抗扭计算公式都是采用实心截面与现实箱形截面杆件有所区别，且按照弹性力学［4］推导的计算公式计算比较繁琐无法运用的实际的工程中，针对这些情况，本文结合工程实际运用中采用弹性力学解析解法和有限元软件ANSYS［5，6］及材料力学简化解分别针对不同的情况进行截面抗扭刚度的结果进行了对比性分析，在一定条件下采用三种计算方法都能达到设计精度的要求，反之采用简化计算方法会产生错误的变化的关系，同时分析了有限元分析方法和弹性力学的解析解的关系，在工程设计应用中供设计者作为参考的依据。

2 经典弹性力学解析解［7］

按照弹性力学矩形截面应力函数φ表达式为

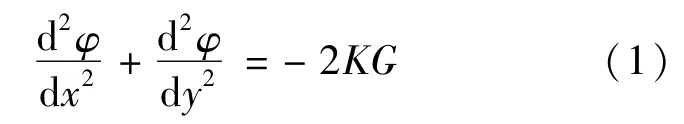
式中 K——截面扭转角；

G——截面的剪切模量。

图1 箱型截面图Fig.1 Box section drawing

对于纯扭转的闭口薄壁截面其应力边界条件为

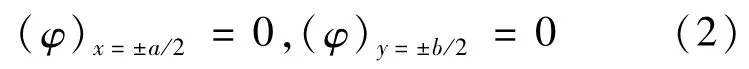
对于横截面边长a／b为任意数值的应力函数表达式为

为了能满足边界条件式（2），可设函数为无穷级数为

将式（4）代入式（1）并满足边界条件式（2）并整理得：

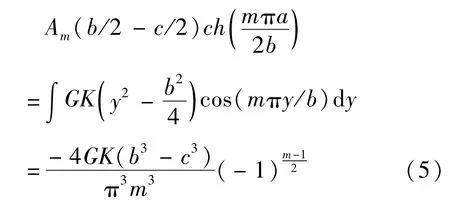
将式（5）代入式（4）及式（3）并整理得应力函数表达式：

式中，c＝b－2t。

由薄膜比拟可以断定，最大剪应力发生在矩形横截面长边的中点，例如A点（x＝0，y＝b／2），其大小为

应力函数表达式为

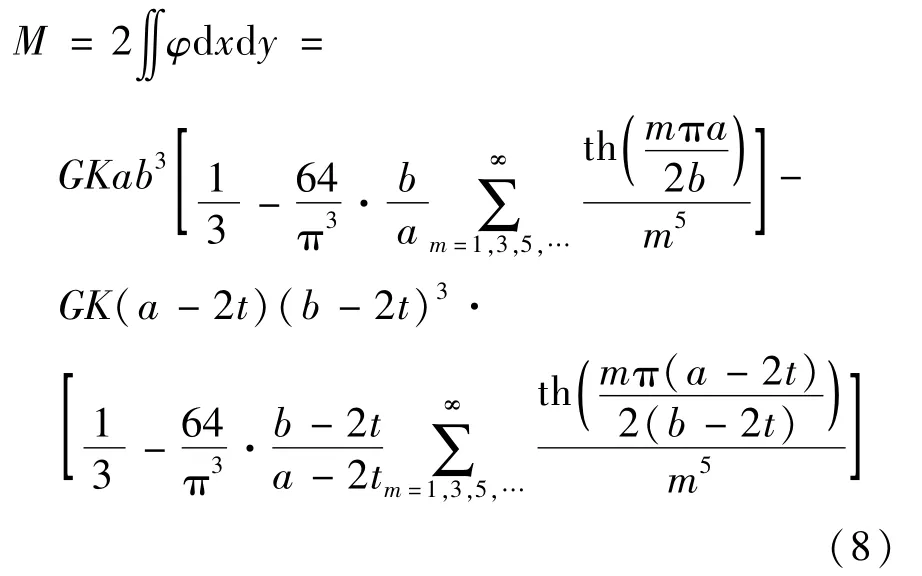
由式（8）得薄壁钢件的最大抗扭刚度为

3 箱形截面扭转刚度简化解

在材料力学［1］中对于闭口薄壁杆件自由扭转杆件规定截面产生的剪应力沿壁厚均匀分布，因此横截面上一点处的剪应力为

对于单位长度的整个闭口杆件的变形能表达式为

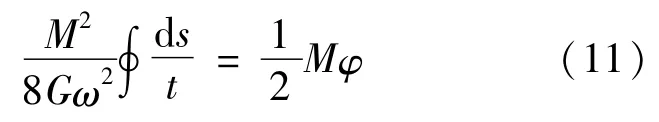
对于杆件壁厚不变的情况下，式（11）整理得：

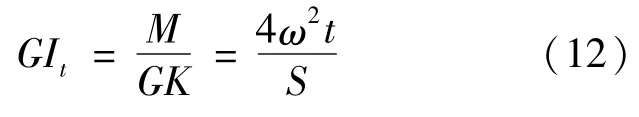
式中 S——截面中线的长度即∮d s；

ω——截面中线所围面积。

4 三种不同计算解法对比

（1）算例1：矩形截面杆件抗扭刚度的计算

对于宽度b＝1 m、长度为a的矩形截面柱体，运用有限元软件ANSYS和弹性力学薄膜比拟原理分别对长宽比相同的矩形截面进行抗扭刚度计算。

从图2中可知两者计算结果一致，表明采用有限元软件ANSYS对截面抗扭刚度计算的正确性。

图2 抗扭刚度—矩形截面长宽比值变化曲线Fig.2 Changing curve of ratio between torsional rigidity-length and width of rectangle section

（2）算例2：等边箱形截面杆件抗扭刚度的计算

对于边长a＝b箱形截面柱体，图3所示为应用弹性力学解析解与材料力学简化解及采用有限元软件ANSYS计算得到的针对不同边长抗扭刚度J—截面厚度与边长t／a的变化曲线。采用三种不同的计算方法的抗扭刚度J-t／a的变化曲线（图3）可知，对于厚宽比t／a≤0.1时采用三种计算方法计算结果基本一致，但对于t／a＞0.1时材料力学简化方法计算结果已偏离弹性力学解析解和ANSYS的计算结果，t／a＞0.25时材料力学简化计算抗弯刚度将产生错误的变化曲线。当t／a≤0.3时采用解析解和ANSYS软件计算截面抗扭刚度J-t／a增大而增大，而t／a＞0.3时采用解析解和ANSYS软件计算截面抗扭刚度J-t／a基本上没变化，即在截面尺寸一定的情况下，在截面厚度增加到一定比例时，在通过增加截面厚度改变截面抗扭刚度已不再适用。

图3 等边箱形截面抗扭刚度—厚宽比值变化曲线Fig.3 Changing curve of ratio between equal-side box torsional rigidity-thickness and width

（3）算例3：等厚薄壁杆件抗扭刚度的计算

在本算例中，对于宽度b＝1 m箱形截面，为了研究针对三种计算方法得到杆件的抗扭刚度与箱型截面长宽a／b的变化关系，取了t＝0.025、0.05、0.1、0.125 m四种不同厚度的箱形截面，图4所示为应用两种不中计算方法计算的截面抗扭刚度的比值—a／b变化关系。

图4 等厚箱形截面计算抗扭刚度比值随长宽比a／b变化曲线Fig.4 Changing curve of equal thickness box section torsional rigidity by length-width ratio

从图4可知，在厚度t一定的箱形截面，运用薄膜比拟法与ANSYS计算的截面抗扭比值随箱形截面长宽比的变化曲线为不规则的变化曲线，但两种方法计算抗扭刚度比值随a／b的增大而减小，且计算抗扭刚度比值基本上在1.1～1.0之间范围内变化。

5 结 论

（1）对矩形截面杆件的扭转刚度计算，采用有限元软件ANSYS计算的截面的抗扭刚度与采用弹性力学薄膜比拟方法计算的结果一致，在工程实际应用中，为了便于简化计算避免解高次方程，应采用有限元软件计算的截面抗扭刚度。

（2）对等边箱型截面，当t／a≤0.1时采用三种计算方法的计算结果比较接近，反之t／a＞0.1时材料力学简化抗扭刚度计算方法已不再使用甚至会产生与实际相违背的结论。在厚宽比t／a≤0.3时采用弹性力学解析解和有限元软件计算截面抗扭刚度J—厚宽比t／b增大而增大，当厚宽比t／a＞0.3时采用解析解和ANSYS截面抗扭刚度随厚宽比t／a增大基本上保持不变。

（3）在不同厚度的薄壁箱形截面，采用弹性力学解析解计算与ANSYS计算的截面抗扭刚度比值比值随a／b的增大而减小，且计算抗扭刚度比值基本上在1.1～1.0之间范围内变化。

（4）在工程设计的应用中，为了提高工程结构的安全系数，能采用ANSYS计算的截面抗扭截面刚度代替薄膜比拟计算的精确解，使有限元软件代替弹性力学解析解在工程应用中具有指导性应用。

［1］ 刘鸿文.材料力学［M］.北京：高等教育出版社，1992.Liu Hongwen.Mechanics ofmaterials［M］.Beijing：Higher Education Press，1992.（in Chinese）

［2］ 于海洋，武建华，李凤佩.对矩形截面杆弹性自由度扭转的探讨［J］.力学与实践，2007，29：73-74.Yu Haiyang，Wu Jianhua，Li Fengpei.Discussion of elestic free torsion of rectangle seceion rod［J］.Mechanics and Practice，2007，29：73-74.（in Chinese）

［3］ 尹刚，冯贤桂.矩形截面杆件扭转的加权残值解法［J］.重庆工学院学报，2005，3（19）：18-20.YiGang，Feng Xiangui.Weighted residualmethod of rectangle section rod torsion［J］.Chongqing Engineering Institute Journal，2005，3（19）：18-20.（in Chinese）

［4］ 程昌钧.弹性力学［M］.兰州：兰州大学出版社，1996.Cheng Changjun.Elastic mechanics［M］.Lanzhou：Lanzhou University Press，1996.（in Chinese）

［5］ 王新敏.ANSYS工程结构数值分析［M］.北京：人民交通出版社，2007.Wang Xinmin.ANSYS engineering structure data analysis［M］.Beijing：China Communications Press，2007.（in Chinese）

［6］ 尚晓江，邱峰，赵海峰，等.ANSYS结构有限元高级分析方法与范例应用［M］.北京：中国水利水电出版社，2005.Shang Xiaojiang，Qiu Feng，Zhao Haifeng，et al.ANSYSadvanced analyticalmethod and sample application［M］.Beijing：China Water Power Press，2005.（in Chinese）

［7］ 薛强.弹性力学［M］.北京：北京大学出版社，2006.Xue Qiang.Elastic mechanics［M］.Beijing：Peking University Press，2006.（in Chinese）

Torsion Stiffness Calculation M ethod of a Box Cross-section Structural M ember

NIU Jinlong1，*JIN Zhiqiang2
（1.Construction and Traffic Committee of Science and Technology Committee of Shanghai，Shanghai200032，China；2.Shenyang Yuanda Aluminum Industry Engineering Co.Ltd.，Shenyang 110027，China）

In engineering applications，box cross-section structuralmembers are used to resist external couple loads.The torsion angle and torsional shear stress are checked in limit state design.However，it is difficult to calculate its torsional rigidity by a classical analytical solution of elasticmechanics.This paper compares three calculation methods-the finite element ANSYS，the membrane analogy of elastic mechanics，and the simplified calculation for the calculation of the torsional rigidity of a rectangular section and a box cross-section.The application limitation for threemethods is proposed.The curve ofδ-a／b is drawn in the same thickness.

coupled moment，box cross-section，torsional rigidity，large deformation，membrane analogy

2013－05－20

*联系作者，Email：niu8888＠vip.sina.com