垃圾填埋场沿底部衬垫双层界面失稳破坏分析
2014-06-28冯世进孙锦剑
冯世进 孙锦剑
(1.同济大学地下建筑与工程系,上海200092;2.同济大学岩土及地下工程教育部重点实验室,上海200092)
1 引言
填埋场底部衬垫系统一般包含双层或多层界面,衬垫系统内的危险界面主要是黏土-土工膜界面和土工织物-土工膜界面。近年来,国内外一些填埋场发生沿底部衬垫界面失稳破坏,使得该类破坏模式得到了国内外的重视。Dixon和Jones建立了单层界面计算模型,将剪切特性为应变软化型的土工织物-土工膜界面作为衬垫系统中的控制界面,分析了垃圾体和填埋场几何构型等参数对填埋场失稳破坏的影响[1]。Filz等考虑了双层界面的影响,利用有限元法对美国Kettleman Hills填埋场进行稳定性分析[2];高丽亚采用随着塑性剪切位移而减小的黏聚力和摩擦角来构建位移软化模型,分析了填埋场衬垫系统中单层和双层界面的剪切位移和剪应力的分布[3]。
近年来,对于接触面的本构模型一直都有学者进行研究,但适用于填埋场衬垫系统的界面本构模型研究较少。Esterhuizen等提出了位移软化模型和功的软化模型,并指出功的软化模型较为适合土工合成材料界面,但功的软化模型较为复杂,难以运用到数值计算中[4];Dixon和 Jones提出了另外一种土工织物界面位移软化本构模型[1],该方法结合传统的摩尔 -库仑理论,以摩擦角和黏聚力来定义界面剪切强度,但该模型较为简单,不能反映复杂条件下土工合成材料界面的软化特性。Anubhav和Basudhar基于邓肯-张模型提出了土与土工织物界面的本构模型[5],但该模型同样不能反映复杂条件下土工合成材料界面的软化特性。
本文考虑土工织物界面的软化特性,将土工织物界面应力应变曲线分为峰前、软化和残余三个阶段,建立了土工织物界面位移软化本构模型,并与实验结果进行对比,验证了该模型的正确性。最后,采用该本构模型分析填埋场底部双层界面衬垫系统的失稳破坏,研究了垃圾体弹性模量、密度、背坡坡度和填埋高度等对界面剪应力和剪切位移的影响。
2 土工织物界面本构模型
本文采用位移软化模型描述土工织物界面的剪切特性,将土工织物界面剪应力随剪切位移的变化分为三个阶段:峰前阶段,软化阶段和残余阶段。
2.1 峰前阶段
峰前阶段的界面剪切特性采用Kondner 1963年提出的双曲线方程来表示[6]:

式中,τ为界面抗剪强度;s为界面剪切位移;1/a为初始剪切模量Ei;1/b为最终抗剪强度τult,根据 b 值,定义破坏率 Rf等于 τp/τult。
试验研究表明,初始剪切模量和正应力可以用下式表示[7,8]:

式中,Ei为初始剪切模量;σn为正应力;γw为水的重度;K为无量纲的剪切系数;Pa为大气压;n为模量指数。
2.2 软化阶段
本文采用位移软化模型来描述界面的软化阶段[4,5],位移软化模型如图 1 所示,其中,sp为峰值剪切位移,sf为峰后剪切位移,sr为残余剪切位移,τp为峰值抗剪强度,τf为峰后抗剪强度,τr为残余抗剪强度,(sf-sp)为峰后位移的增加值,(sr-sp)为残余位移与峰值位移之差,(τp-τf)为峰后强度的减小值,(τp-τr)为峰值强度与残余强度之差。
下面通过无量纲形式表达界面位移软化特性:
(1)把软化阶段的应力位移曲线转化成(sf-sp)-(τp-τf)曲线。
(3)画出S-D曲线,用双曲线进行模拟,得到如下关系式:
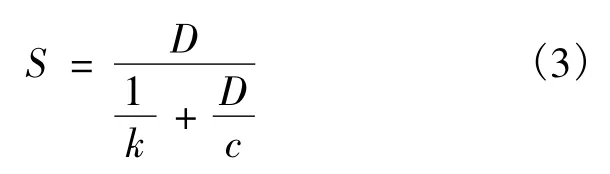
式中,k为曲线的初始斜率;c为水平渐近线与S轴上的截距。
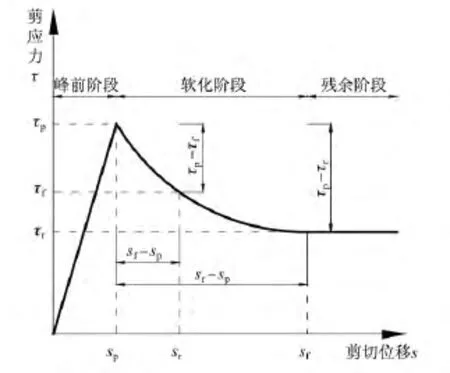
图1 位移软化模型Fig.1 Displacement softening model
2.3 残余阶段
残余阶段为最后阶段,此时,随着剪切位移的增加,界面抗剪强度不再增加,达到残余强度值,即:

式中,φr为残余摩擦角;cr为残余黏聚力。
3 计算模型的应用与验证
3.1 试验介绍
文献[9]中设计了一个垃圾填埋场衬垫系统大型斜坡模型试验,试样宽度为1 m,长度为4.5 m,最大正应力为75 kPa。该试验采用GT和GM两种土工合成材料组成的单界面衬垫系统,如图2所示。为了保障GT最终不会产生拉伸破坏,GT/GM单界面试验选取较小的正应力为35 kPa。根据GT/GM界面峰值摩擦角随正应力的变化规律,为保证实验加载至35 kPa时GT/GM界面发生滑移,斜坡坡角定为35°。试验利用砂土堆载产生的沿斜坡方向的下滑力模拟垃圾填埋场施加在衬垫系统上的剪力,进而研究剪应力在衬垫系统内部的传递机理。本文将提出的界面本构模型嵌构在FLAC2D有限差分程序中,分析该模型试验的结果。

图2 GT/GM界面试验模型示意图Fig.2 Testing model of GT/GM interface
3.2 模型的建立与验证
分析大型斜坡模型试验沿底部衬垫界面的失稳破坏时按平面应变问题考虑,以斜坡的典型剖面作为研究对象,尺寸和边界条件均与试验一致。土体采用摩尔-库伦模型,剪切模量G为1×108Pa,体积模量B为2×108Pa,密度ρ为2 258 kg/m3,黏聚力c为0 kPa,摩擦角φ为35°;土工织物界面采用前文提出的软化模型进行模拟,土工织物厚度为2 mm,拉伸模量为7×106Pa,界面法向刚度为2×108Pa/m,界面的峰值黏聚力为5 kPa,峰值摩擦角为19°,残余黏聚力为3 kPa,残余摩擦角为12.8°。在计算过程中,每级施加10 kN荷载,总荷载为180 kN,根据砂土密度和模型尺寸可以推算出每一级填埋的高度为0.12 m,总高度为2.16 m。
图3为数值模拟与试验结果的对比曲线,可以发现随着加载重量的增加,数值模拟得到的界面位移发展趋势与实验结果得到的界面位移发展趋势较为吻合,且两者数值接近。这说明本文提出的三阶段界面本构模型能用于模拟填埋场稳定分析。

图3 土工织物0.1 m处界面位移对比曲线Fig.3 Comparison of interface displacement of geotextiles at 0.1 m
4 填埋场沿底部衬垫系统界面失稳破坏分析
4.1 计算模型的建立及参数选取
本文根据上述的界面本构模型,研究填埋场底部存在双层界面剪切破坏时,剪应力和剪切位移的发挥过程。计算模型如图4所示,图中最底层为下卧地基土,上面为垃圾体,地基土与垃圾体之间为衬垫系统。图5为衬垫系统界面的局部放大图,土工织物采用梁单元模拟;该模型共有180个界面单元,上层界面为土工布(GT)/土工膜(GM)界面,下层界面为土工膜(GM)/地基土界面。
填埋场基底水平长度为L,填埋高度为H,填埋场背坡坡度为1/S1,垃圾体前坡坡度为1/S2。在计算模型中下卧地基土网格在水平和垂直方向均被固定,其他所有网格内的区域都可以在任何方向自由运动。基本工况如下:垃圾体采用摩尔-库仑模型,黏聚力c为5 kPa、摩擦角φ为25°;地基土的弹性模量E为3.0×l07Pa,泊松比υ为0.3、密度 ρ为 1 900 kg/m3、体积模量 B 为 25 MPa、剪切模量为 11.5 MPa、内摩擦角 φ 为 20°、黏聚力c为10 kPa。GT/GM界面法向刚度为4.0×107Pa/m,界面的峰值黏聚力为2.3 kPa,峰值摩擦角为16°,残余黏聚力为 1.8 kPa,残余摩擦角为9°。GM/地基土界面法向刚度为4.0×107Pa/m,界面的峰值黏聚力为3.2 kPa,峰值摩擦角为 24.5°,残余黏聚力为 2.5 kPa,残余摩擦角为12.8°。计算中认为地基处于稳定状态,不考虑地基的破坏。

图4 填埋场剖面示意图Fig.4 Schetch of landfill hillslope
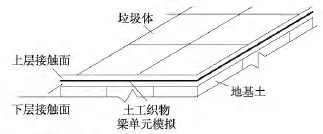
图5 接触面局部放大图Fig.5 Local amplified figure of interface
4.2 垃圾体弹性模量的影响
图6(a)为垃圾体弹性模量E变化时GT/GM界面基底和背坡处位移的变化曲线。可以发现,随着垃圾体弹性模量的增加,基底处界面位移逐渐增大而背坡处界面位移逐渐减小;当垃圾体弹性模量从500 kPa增加到2 000 kPa时,基底最大位移从27 mm增大到35 mm,背坡最大位移从55 mm减小到52 mm。但总体来说,垃圾体弹性模量对界面位移的影响不大。图6(b)为垃圾体弹性模量E变化时GM/地基土界面基底和背坡处位移的变化,结果与GT/GM界面相似。
图7(a)为垃圾体弹性模量E变化时GT/GM界面基底和背坡处剪应力的变化曲线。根据图7(a)及表1可以发现,随着垃圾体弹性模量的增加,基底处界面剪应力逐渐增大而背坡处界面剪应力基本不变;当垃圾体弹性模量从500 kPa增加到2 000 kPa时,基底最大剪应力从27.6 kPa增大到31.4 kPa,但总体来说垃圾体弹性模量对界面剪应力的影响不大。图7(b)为垃圾体弹性模量E变化时GM/地基土界面基底和背坡处剪应力的变化曲线,结果与GT/GM界面相似。

图6 垃圾体弹性模量变化时GT/GM和GM/地基土界面位移变化曲线Fig.6 Effect of MSW elastic modulus on interface displacement
4.3 垃圾体密度的影响
图8(a)为垃圾体密度ρ变化时,GT/GM界面基底和背坡处位移的变化曲线。可以发现,随着垃圾体密度的增加,基底和背坡处界面位移都逐渐增大,但背坡处增幅较大;当垃圾体密度从1 000 kg/m3增加到1 600 kg/m3时,基底最大位移从22 mm增大到36 mm,背坡最大位移从49 mm增大到65 mm。图8(b)为垃圾体密度ρ变化时,GM/地基土界面基底和背坡处位移的变化曲线,变化规律与GT/GM界面一致。

图7 垃圾体弹性模量变化时GT/GM和GM/地基土界面剪应力变化曲线Fig.7 Effect of MSW elastic modulus oninterface shear stress
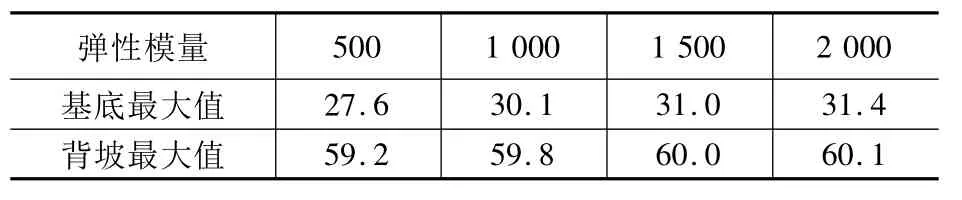
表1 GT/GM界面接触面最大剪应力Table 1 The maximum shear stress of GT/GM interface kPa

表2 GM/地基土界面接触面最大剪应力Table 2 The maximum shear stress of Gu/soil interface kPa
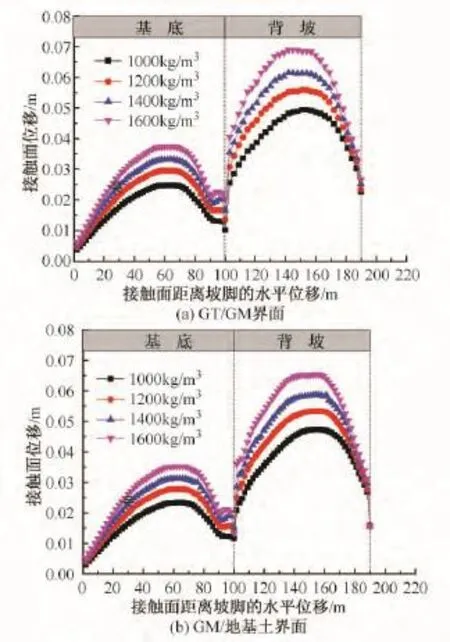
图8 垃圾体密度变化对GT/GM和GM/地基土界面位移的影响Fig.8 Effect of MSW density on interface displacement

图9 垃圾体密度变化时,GT/GM和GM/地基土界面剪应力变化曲线Fig.9 Effect of MSW density on interface shear stress
图9(a)为垃圾体密度变化时GT/GM界面基底和背坡处剪应力的变化曲线,可以发现随着垃圾体密度从1 000 kg/m3增加到1 600 kg/m3,基底最大剪应力从22 kPa增加到34 kPa,背坡最大剪应力从49 kPa增加到74 kPa。图9(b)为垃圾体密度变化时GM/地基土界面基底和背坡处剪应力的变化。可以发现,剪应力随垃圾体密度变化的曲线与GT/GM界面剪应力随垃圾体密度的变化曲线较为一致。
4.4 填埋场背坡坡度的影响
图10(a)为垃圾体背坡坡度S1变化时,GT/GM界面基底和背坡处位移的变化曲线。可以发现,随着垃圾体背坡坡度的增加,基底处界面位移变化很小,而背坡处在坡度为1/2.5时迅速增大,这表明此时界面已经发生失稳破坏。图10(b)为垃圾体背坡坡度变化时,GM/地基土界面基底和背坡处位移的变化曲线,可以发现,背坡坡度变化对GM/地基土界面影响不大,这可能是因为该界面抗剪强度参数较大所致。

图10 填埋场背坡坡度的变化对GT/GM和GM/地基土界面位移的影响Fig.10 Effect of back slope gradient of landfill on interface displacement
图11(a)为垃圾体背坡坡度S1变化时,GT/GM界面基底和背坡处剪应力的变化曲线。可以发现,随着垃圾体背坡坡度的增加,基底处界面剪应力变化很小,而背坡处在坡度为1/2.5时迅速增大,这也导致该界面位移迅速增大。图11(b)为垃圾体背坡坡度变化时,GM/地基土界面基底和背坡处剪应力的变化曲线,结论与界面剪切位移的变化曲线较为一致。
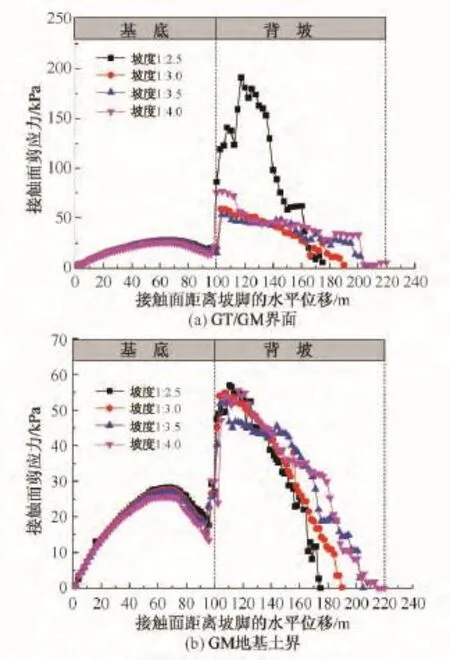
图11 填埋场背坡坡度的变化对GT/GM和GM/地基土界面剪应力的影响Fig.11 Effect of back slope gradient of landfill on interface shear stress
4.5 垃圾体填埋高度的影响
图12(a)为垃圾体填埋高度变化时GT/GM界面基底和背坡处位移的变化。可以发现,随着垃圾体高度的增加,基底和背坡处界面位移都逐渐增大,且增幅都较大;当垃圾体填埋高度从20 m增加到40 m时,基底最大位移从17 mm增大到51 mm,背坡最大位移从22 mm增大到90 mm。图12(b)为垃圾体填埋高度变化时GM/地基土界面基底和背坡处位移的变化,变化曲线与GT/GM界面一致。

图12 垃圾体填埋高度对GT/GM和GM/地基土界面位移的影响Fig.12 Effect of landfill height on interface displacement
图13(a)和图13(b)分别为垃圾体填埋高度变化时,GT/GM界面和GM/地基土界面基底和背坡处剪应力的变化。可以发现,剪应力随垃圾体填埋高度变化的曲线与界面位移的变化曲线较为一致。
4.6 上下界面剪应力和剪切位移对比分析
垃圾填埋场衬垫系统存在多个界面,使得失稳破坏时的滑移面存在不确定性。为了研究填埋场沿何种界面发生失稳破坏,本文采用上节的基本工况,并在垃圾体弹性模量为1 000 kPa,密度为1 200 kg/m3,填埋高度为30 m,背坡坡度为1/3的条件下进行GT/GM和GM/地基土两个界面的剪应力和剪切位移分析。计算结果如图13所示。
图14(a)为GT/GM界面与GM/地基土界面基底和背坡处剪切位移变化的对比曲线。可以发现,GT/GM界面最大剪切位移基底为32 mm,背坡为52 mm,略大于GM/地基土界面的30 mm和49 mm。图14(b)为GT/GM界面与GM/地基土界面基底和背坡处剪应力变化的对比曲线。可以发现,GT/GM界面基底与背坡的剪应力稍大于GM/地基土界面。
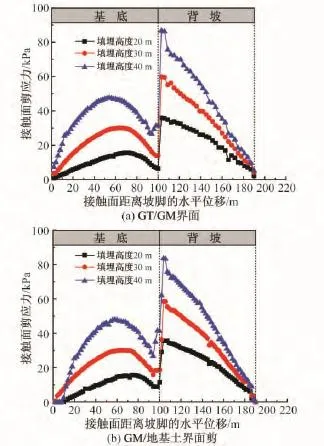
图13 垃圾体填埋高度变化对GT/GM和GM/地基土界面剪应力的影响Fig.13 Effect of landfill height on interface shear stress

图14 GT/GM界面和GM/地基土界面剪应力和剪切位移对比曲线Fig.14 Interface shear stress and displacement on the interface of GT/GM and GM/soil
以上分析结果表明,在此种工况下,填埋场的危险界面为GT/GM界面,出现这种情况的原因主要是本文采用的GT/GM界面强度参数小于GM/地基土界面。由此可见,填埋场发生失稳破坏的界面往往是抗剪强度较小界面,这与文献[9]结论一致。
5 结论
运用三阶段界面本构模型对填埋场底部衬垫系统双层界面的模拟分析可以得到如下结论:
(1)填埋场界面剪切特性可以分为峰值阶段、残余阶段和软化阶段,本文提出了三阶段界面本构模型并与试验结果进行了对比。
(2)随着垃圾体弹性模量增加,基底处界面剪切位移和剪应力逐渐增大,而背坡处界面剪切位移和剪应力的影响逐渐减小。
(3)随着垃圾体填埋高度和密度的增加,界面的剪应力和剪切位移均逐渐增大,而背坡坡度对界面剪切位移影响较大。
(4)界面失稳破坏往往发生在抗剪强度较小界面。
[1] Dixon N,Jones D R V.Landfill lining stability and integrity:the role of waste settlement[J].Geotextiles and Geomembranes,23(1):27-53.
[2] Filz G M,Esterhuizen J B,Dunean J M.Progressive failure of lined waste impoundments[J].Journal of Geotechnicaland GeoenvironmentalEngineering,2001,127(10):84-848.
[3] 高丽亚.垃圾填埋场沿底部衬垫界面失稳破坏及土工膜拉力研究[D].上海:同济大学,2007.Gao Liya.Analysis of instability failure of landfill along geosynthetic interface and tension of geomembranes placed on landfill slope[D].Shanghai:Tongji University,2007.(in Chinese)
[4] Esterhuizen J B,Filz G M,Dunean J M.Constitutive behavior of geosynthetic Interfaces[J].Journal of Geotechnicaland GeoenvironmentalEngineering,2001,127(10):83-540.
[5] Anubhav,Basudhar P K.Modeling of soil-woven geotextile interface behavior from direct shear test results[J].Geotextilesand Geomembranes,2010,28(11):403-408.
[6] Kondner R L.Hyperbolic stress-strain response:cohesive soils[J].Journal of Soil Mechanics and Foundations Division,1963,89(1):289-324.
[7] Jnabu N.Soil compressibility as determined by oedometer and triaxial tests[C].European Conference on Soil Mechanics and Foundations engineering,Wiesbaden,Germany,1963,1:19-25.
[8] Seo M W,Park J B,Park I J.Modeling of interface shear behavior between geosynthetics[J].Journal of Civil Engineering,2003,7(1):9-16.
[9] 林伟岸.复合衬垫系统剪力传递、强度特性及安全控制[D].杭州:浙江大学,2009.Lin Weian.Shear stress transfer,strength characteristics and safety control of composite liner systems[D].Hangzhou:Zhejiang University,2009.(in Chinese)
