分光计调节途径优化的理论探讨

叶丽军，许富洋，范晓珍

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

·实验科学理论·

分光计调节途径优化的理论探讨

叶丽军，许富洋，范晓珍

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

在普物实验中，分光计的调节和使用作为一个经典的实验项目被普遍采用，但在其调节过程中往往带有一定的机械性和偶然性，对初学者有较大的困扰。针对关键的细调环节，通过对渐近法调节原理的探讨，从理论上得出了反射镜法线和望远镜光轴偏离程度及调节到位情况的直接判据，可实现反射镜和望远镜的分离调节，使学生在调节中能真正做到“知其然，知其所以然”，优化调节途径，有利于初学者快速掌握分光计调节的原理和技巧。

分光计；渐近法；十字叉丝反射像；分离调节

分光计是一种精密的测角仪，其基本结构和调节方法在某种程度上可以说是现代一些光谱仪、单色仪的简易原型，是一种典型的光学仪器。在普物实验中，分光计的调节和使用作为一个经典的实验项目被普遍采用，但学生在实验中往往感到难度较大，是一个疑难实验[1_2]。

有关分光计的调节技巧及相关问题已有较多的探讨[3_5]，其中，分光计细调是最重要、最关键的一环，而渐近法(又称各半调节法)是细调最有效的调节方法[6]。各种调节技巧的本质往往是对渐近法传统调节途径的改进和优化[7_9]，但目前鲜有文献进行渐近法调节途径优化的理论探讨，这对于学生全面掌握分光计调节技巧是不利的。本文拟在这方面进行一些探索，使学生在调节中能真正做到“知其然，知其所以然”。

1 渐近法调节原理

假设分光计粗调后如图1所示，其中M表示双面反射镜;n为其法线方向;y轴表示分光计的转轴;χ表示分光计调节完毕后(即望远镜的光轴与分光计旋转轴垂直)的望远镜光轴;α表示入射光线N(即望远镜的光轴)与χ轴间的夹角;β表示M与y轴之间的夹角;θ表示入射光线N与反射光线N＇间的夹角。

为了讨论方便，作如下规定：α由入射光线N转至χ轴、β由M转至y轴、θ由反射光线N转至入射光线N。若为顺时针，α、β、θ取正数，反之取负数。

如图1所示的状态有：

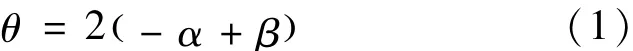
分光计调节完毕的状态为：θ=α=β=0。

调节时，分别调望远镜高度调节螺丝和载物台调平螺丝，使望远镜中十字叉丝反射像与调整用叉丝的垂直距离各减少一半，并最终达到重合状态，则N、N＇重合于原∠NOn的平分线上。如图2(a)所示，各角度变为：

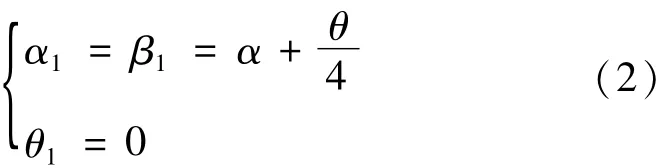
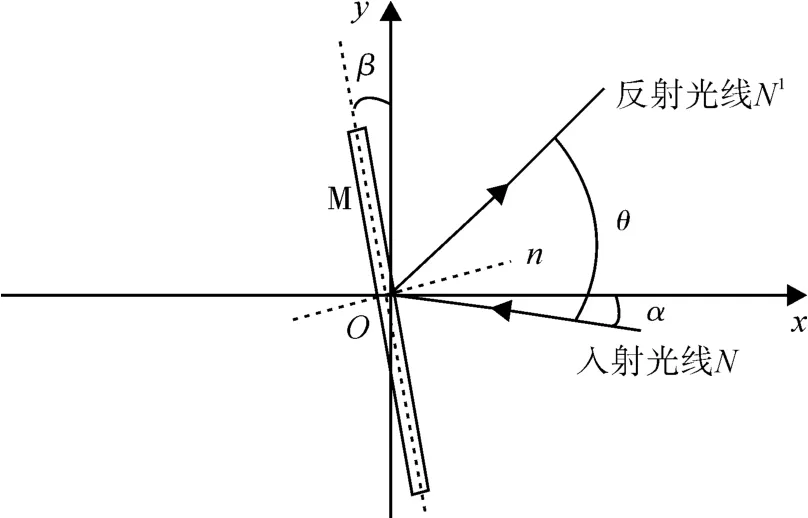
图1 粗调后分光计的状态

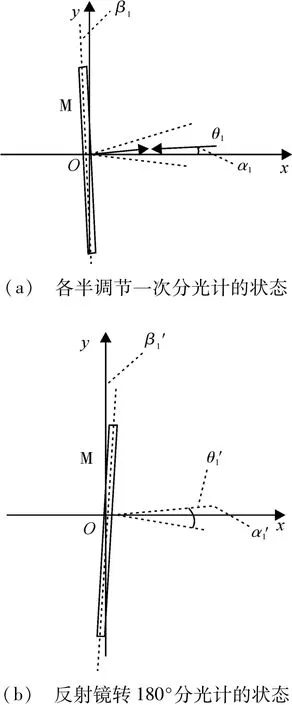
图2 渐近法调节过程示意图

然后旋转载物台使双面反射镜转过180°，如图2(b)所示，则：

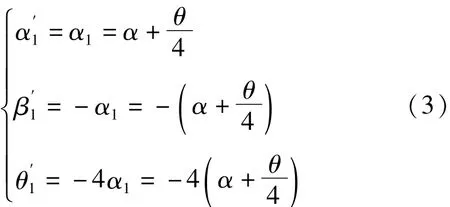
此时，再次调望远镜高度调节螺丝和载物台调平螺丝，使望远镜中十字叉丝反射像与调整用叉丝的垂直距离各减少一半，则N、N＇与χ轴完全重合，θ2=α2=β2=0，即采用渐近法调节，只需经过两次调整，就可达到调节目标。从理论上看，第一次调整时，通过各半调节将处于随机状态的α、β调至相等，达到式(2)的状态;接着将反射镜旋转180°，各角度变为式(3)的状态，再次进行各半调节。结合式(1)～式(3)可知，当再次达到式(2)的状态时，α、β、θ值为0，调节完成。

2 渐近法调节途径优化原理探讨

由于实验教学对象大多是初学者，在操作中往往不能象理论预期的那样，经过两次调节就达到目的。实际上，即使是很有经验的操作者也要通过多次调节才能调好，这是因为精确严格的各半调节难以实现。如图1所示，假设在多次调节过程中有如下两个状态，即：

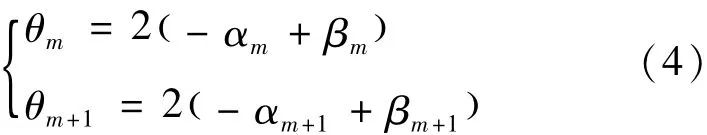
两式作差得：

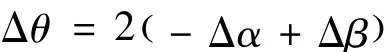
式中：Δα、Δβ分别对应于调节过程中望远镜高度调节螺丝和载物台调平螺丝的调节;Δθ则对应于调节中十字叉丝反射像的移动;可以认为Δα、Δβ为自由变量，而Δθ为应变量。传统的渐近法调节往往是依次对双面反射镜的两个面反复进行Δα、Δβ的各半调节，当某一面调节完成时，有

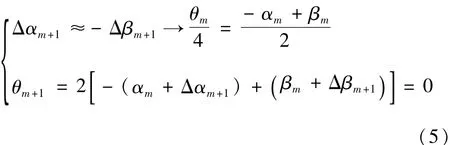
由式(3)可知，这样的操作对另一面造成的影响是：θ

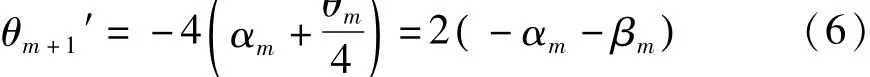
根据式(4)和式(6)可知，第m+1次调整对θm和θm+1＇不产生影响，但由于分光计望远镜视场较小(约为3°24＇)[10]，而m+1次调整改变了入射光线的方向，因此很容易出现一面调节完成，转至另一面十字叉丝反射像偏离或消失的情况。分光计调节的目标是使α、β、θ同时趋向0，而传统的渐近法调节仅将θm+1→0作为调节判据，缺乏对反射镜和望远镜偏离情况的分析，调节时采用式(5)方式，“胡子眉毛一把抓”，对某个面的有效调节可能会对另一个面的状态造成较大破坏，存在较多的冗余操作，调节效率不高。

比较式(4)和式(6)可以得出：(1)若αm=0，则θm和θm+1＇异号，两个面的十字叉丝反射像位于调整用叉丝的异侧，如图3(a)所示，两个面的反射像关于调整用叉丝在垂直方向呈一上一下对称分布。此时可控制αm不变，仅改变Δβm，即调节时仅对载物台调平螺丝进行调整，使两个面的十字叉丝反射像向调整用叉丝逼近;(2)若βm=0，则θm和θm+1＇同号，两个面的十字叉丝反射像位于调整用叉丝的同侧，如图3(b)和图3(c)所示，两个面的反射像关于调整用叉丝在垂直方向呈同上同下等高分布。此时可控制βm不变，仅改变Δαm，即调节时仅对望远镜高度调节螺丝进行调整，使两个面的十字叉丝反射像向调整用叉丝逼近。

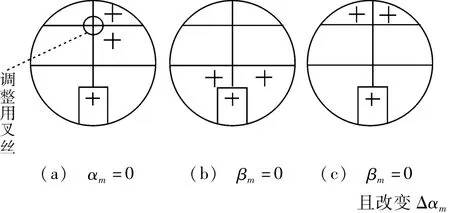
图3 十字叉丝反射像分布示意图

具体实验时，α、β通常均不为0，即反射镜法线和望远镜光轴均不水平。但由上述分析可知，可将α、β作为独立的自由变量进行分离调节，即通过对载物台调平螺丝的调节，使两个面的十字叉丝反射像等高(可将此现象视为β→0的判据);通过对望远镜高度调节螺丝的调节，使两个面的十字叉丝反射像的中心位置与调整用叉丝等高(可将此现象视为α→0的判据)，从而最终使θ→0。这样，变传统调节的结果判据为过程判据，变Δα、Δβ的同步调节为分离调节，将调节幅度与偏离程度关联起来，可减少式(5)的盲目性，确保每一次操作的纯粹性和有效性。

3 结束语

渐近法调节是一种巧妙而有效的分光计细调方法，但传统的调节方式带有一定的机械性和偶然性，对初学者有较大的困扰。通过对渐近法调节原理的探讨，可以发现根据反射镜两个面的十字叉丝反射像与调整用叉丝的位置关系，能得到反射镜法线和望远镜光轴偏离程度及调节到位情况的直接判据;可实现反射镜和望远镜的分离调节，优化调节途径，同时可增强操作的直观性，有利于初学者快速掌握分光计调节的原理和技巧。

[1]张锐波，潘克宇，刘建平.分光计调整难点原理图析[J].山西师范大学学报：自然科学版，2005，19(1)：61_63.

[2]杨百愚，冯大毅.分光计调整实验中望远镜的调整技巧[J].大学物理，2005，24(4)：45_47.

[3]王小怀.分光计调节和使用中的困难及解决措施[J].实验室研究与探索，2007，26(2)：35_37.

[4]李伟，潘玲珠.分光计调节难点剖析[J].实验科学与技术，2008，6(3)：27_28.

[5]高国棉，杨百愚，王益军，等.两步到位快速调节分光计[J].物理与工程，2009，19(3)：12_15.

[6]何丽.快速调节分光计的有效方法[J].实验科学与技术，2009，7(3)：29_30，147.

[7]赵宗坤.分光计调节方法的优化[J].实验科学与技术，2010，8(3)：31_33.

[8]王卫星，冯中营.分光计中望远镜的调节原理[J].大学物理实验，2010，23(3)：15_16.

[9]张敏园，张世功.光路分析在分光计调整中的作用[J].大学物理实验，2010，23(5)：56_58.

[10]陈艳山，闵爱琳，陈明伟.分光计望远镜视场角的研究[J].大学物理实验，2004，17(1)：50_53.

Theoretical Discussion about the Optim ization of the Spectrometer Ad justment

YE Lijun，XU Fuyang，FAN Xiaozhen
(College of Mathematics，Physics and Information Engineering，Zhejiang Normal University，Jinhua 321004，China)

The adjustment and usage of spectrometer is a typical experiment in the college physics experiments，but there is always a great puzzle for beginners for itsmechanical process and accidental results of adjustment in some ways.In regard to the significant step of fine adjustment，the direct criteria of the degree of the deviation and adjustment of the reflector normal and telescope axiswere obtained in theory according to the analysis ofasymptotic adjustment.Thus，the spectrometer adjustment can be optimized by adjusting the reflector and telescope separately.Besides，itwill help students to understand and master the principles and skills of adjustment better.

spectrometer;asymptoticmethod;the“+”image;separate adjustment

O435.1

A

10.3969/j.issn.1672_4550.2014.01.043

2012_12_28

金华市科学技术研究计划项目（2010_1_052）；浙江师范大学教改项目。

叶丽军（1980_），女，工程师，主要从事大学物理实验教学与研究工作。