数学解题常用的六种逆向思维方法

■江思容

数学解题常用的六种逆向思维方法

■江思容

数学学习离不开思维，思维能力的发挥和思维活动的发展决定了学习效果的高低。只有科学地把握思维特点，才能够从总体上把握事物的本质特征。在教学解题中常常运用逆向思维，它大致有六种常用方法。

一、反客为主

反客为主，换而言之，就是要将常量当作变量，将变量当作常量，变量与常量既统一，又互相转化，是一个相互矛盾的统一体。反客为主的思维方法是一种很好的思维方法。

例1当m是什么整数时，关于x的方程x2－（m－1）x+m+1=0的两根都是整数？

【方法导引】因为关于x的方程有解，那么关于m的方程也应有解，且解都是整数，故先解关于m的方程。

解：以m为主元，已知方程化为（x－1）m=x2+x+1

∴x－1=±1，±3，

∴x=2，0，4，－2

把x以上述值依次代入m的表达式得：m=7或－1。

二、无中生有

有时需要巧妙地造出与原问题有关的新元素和新模型来对某些数学问题进行解决，这就是无中生有。

（1）若方程没有实数根，求p的范围。

（2）若p>0，问p为何值时，方程有两个相等的实数根，并求出这两个根。

【方法导引】首先要弄清无理方程没有实根的含意是将其换元后所得的一元二次方程的解求出，令其解小于零，这样就可以求出p的范围。

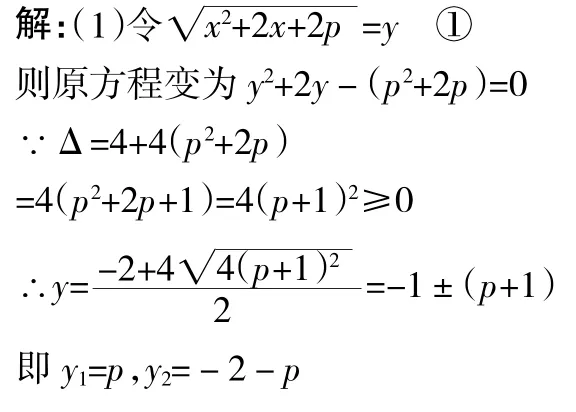
解这个不等式组得，－2＜p＜0

（2）∵p>0，把y1=p代入①得

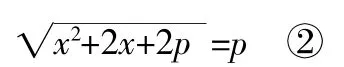
而y2=－2－p＜0（不合题意，舍去）

将②式平方，整理得

x2+2x－（p2－2p）=0③

令Δ=4+4（p2－2p）

=4（p2－2p+1）=4（p－1）2=0

解之得：p=1

当p=1时，原方程有两个相等实根，把p=1代入③得x2+2x+1=0，

∴x1=x2=－1，经检验，当p=1时，

x1=x2=－1是原方程的根。

三、声东击西

提出一个问题往往比解决一个问题更重要,因为解决问题也许仅是一个数学上或实验上的技能而已。而提出新的问题、新的可能性,从新的角度去看旧的问题,都需要有创造性，声东击西是一种很好的方式，可以通过另外一个问题的解决来对原问题进行间接解决。

【方法导引】由已知条件直接求出代数式的值繁而难，若根据题目所给的条件，巧妙地利用方程知识进行求解，就方便得多，于是采用声东击西的策略，达到由此及彼的目的。

四、以退为进

解数学题有时候要以退求进，有时候要先进后退，恰当运用进退的互化是辩证思维的一条重要方法。

例4如图，△ABC中AE是∠A的外角平分线，D是AE上任意一点，试确定AB+AC与BD+CD之间的大小关系。

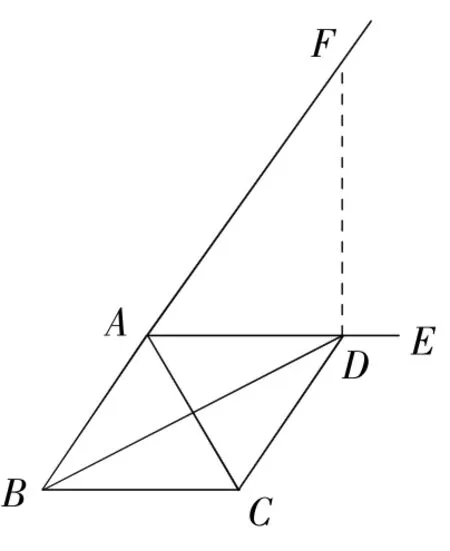
【方法导引】D为AE上任意一点，说明D点有随意移动的特性，给问题的研究带来了难度，我们巧借D点可动的情况，取特殊的位置①D与A重合；②AD⊥CD加以研究，收到以静止动，以退求进的效果。①当D与A重合时，显然有AB+AC=BD+CD；②当CD⊥AD时，只要延长CD交BA的延长线于F，由等腰三角形性质及两边之和大于第三边的特性不难证明AB+AC＜BC+CD，综①，②启发我们证明，AB+AC≤BD+CD。

解：要确定的关系是AB+AC≤BD+ CD，下面对此结论加以证明。

如上图，在BA的延长线上取点F，使AF=AC，连DF。

显然△AFD≌△ACD，

则DC=DF，

又AC=AF，

故AB+AC=AB+AF＜BD+DF=BD+ CD。

当D与A重合时，AB+AC=BD+CD

综上得，AB+AC≤BD+CD

五、分而治之

有些数学问题我们想从整体上考虑比较困难时，我们不妨采用分而治之的方法来处理，即将问题划分为几种情况（或类型），各个击破，分而治之。

例5当a为何值时，方程

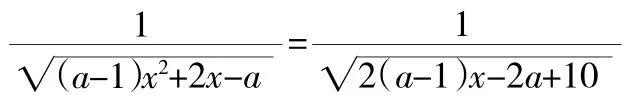
的解只有一个？

【方法导引】这是一个根式方程，应变换为等价的方程（方程组），注意到a=1或a≠1时，已知方程有本质的不同，因此应对这两种情况分别讨论。进而，为讨论何时只有一个解，又要进行第二级分类。

解：化简变形得到与原方程同解的不等式组

六、出奇制胜

奇兵能克制强敌，巧解可轻取难题，难题之难就在于条件与结论之间的内在联系比较隐蔽，欲揭示这种内在联系，如循常规老路，必费时费力，只有敢于创新，才能以巧取制。

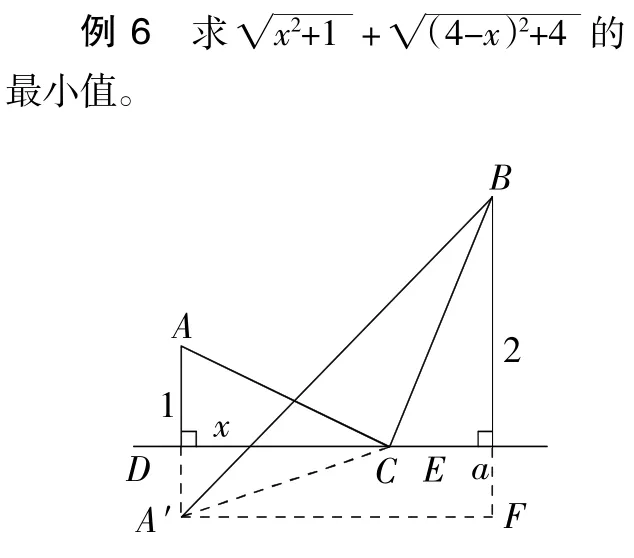
解：构造如图所示的Rt△ACD，Rt△BCE，使AD=1，BE=2，CD=x，DE=4，且CD、CE在直线a上，则所求最小值转化为“在直线a上求一点C，使AC+ CB的值最小”。

（作者单位：武汉市洪山中学）

责任编辑 王爱民