有限群的广义转移

刘 秀，韦华全，马儇龙

（1.昭通学院数学与统计学院，云南昭通657000；2.广西师范学院数学科学学院，广西南宁530023；3.广西大学数学与信息科学学院，广西南宁530004；4.北京师范大学数学科学院，北京100875）

有限群的广义转移

刘 秀1，韦华全2，3，马儇龙4

（1.昭通学院数学与统计学院，云南昭通657000；2.广西师范学院数学科学学院，广西南宁530023；3.广西大学数学与信息科学学院，广西南宁530004；4.北京师范大学数学科学院，北京100875）

给出了有限群广义置换表示和广义转移映射的概念，推广Burnside定理.

有限群；广义置换表示；广义转移；p-幂零

确定一个已知群的非单性或可解性，是群论中最重要的课题之一，其中单项表示方法和转移方法是行之有效的研究方法.本文提出广义置换表示和广义转移映射的概念，目的是推广Burnside定理，为研究有限群的非单性、p-幂零性和可解性打下基础.

1 基本定义及引理

定义1（参见文献［1］定义1） 设G1，G2是群，映射f：G1→G2叫做G1到G2的广义同态映射，记为G1G2，如果∀a，b∈G1，等式（ab）f＝afbf和（ab）f＝bfaf至少有一个成立.当f为同态时，可简记G1～G2；当f为反同态时，亦可记G1G2.

定义2（参见文献［2］定义2） 设G是群，称群G广义作用在非空集合Ω上，如果G到变换群SΩ有一个广义同态，即对每个元素x∈G，对应Ω上的一个变换φ（x）：α｜→αx，并且满足（αx）y＝αxy，或者（αy）x＝αxy，这里x，y∈G，α∈Ω.

定义3 所谓群的广义置换表示指的是群到置换群中的广义同态.

例1 设G是群，H≤G，取Ω＝｛Hx｜x∈G｝为H的全体右陪集的集合.作如下映射：P：G→SΩ，其中P（g）：Hx｜→Hxg，或P（g）：Hx｜→Hxg-1，∀Hx∈Ω，∀g∈G.由于

假定

则τ（g）是集合｛1，2，…，n｝的一个广义置换，而τ可看成是G到对称群Sn内的广义同态映射.

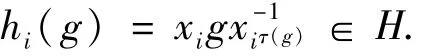
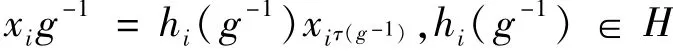
所谓G到H内的广义转移指的是G到H／H′内的映射VG→H，满足

定义5（参见文献［3］5.3定义Ⅱ） 设G是有限群，P是G的Sylow p-子群.如果G有正规子群N，满足N∩P＝1，NP＝G，则称G为p-幂零群，而称N为G的正规p-补.

引理1（参见文献［3］4.9命题Ⅰ） G′是G的全不变子群，并且若N◁G，则G／N是交换群⇔N≥G′.

2 主要结果

定理1 1）VG→H是G到H／H′内的广义同态；

2）VG→H不依赖于H的陪集代表的选取；

证明 1）设g1，g2∈G，则

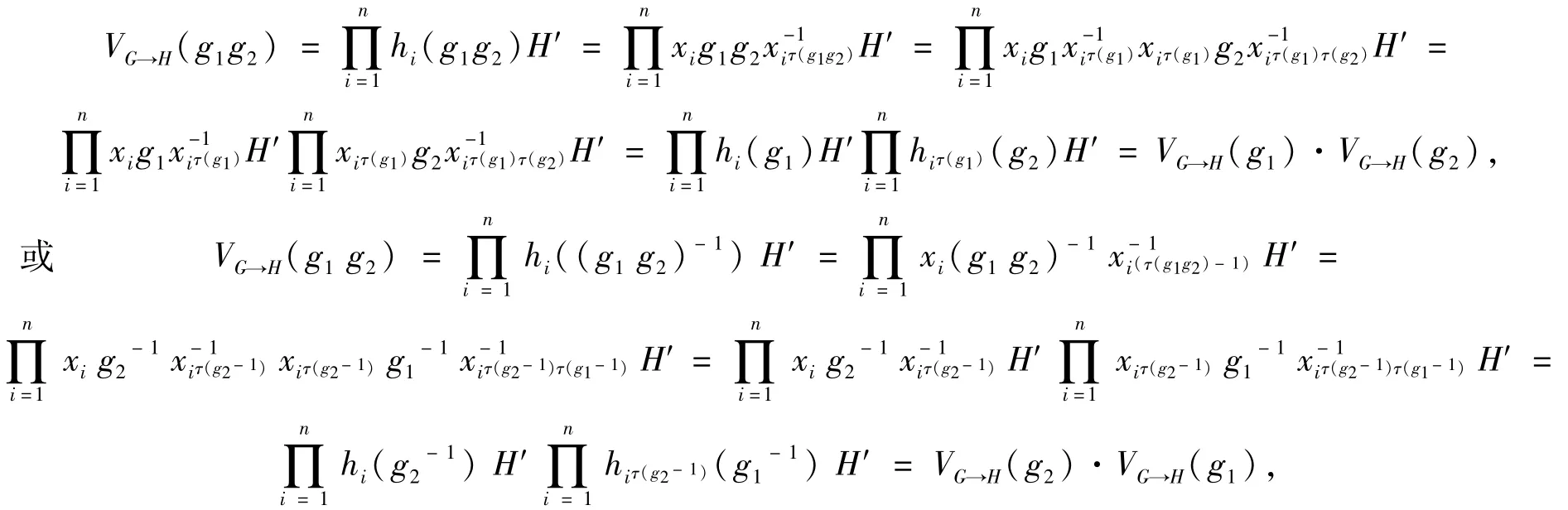
故VG→H是广义同态.

或

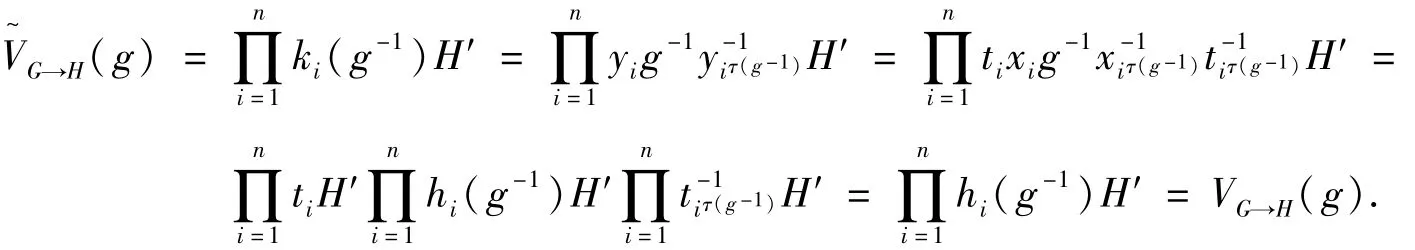
对于任意的h∈H，设yjh＝kj（h）yjσ（h）或yjh-1＝kj（k-1）yjσ（h-1），其中kj（h），kj（h-1）∈K，σ是H在K上的广义置换表示得到的H到Sm中的广义同态.于是有

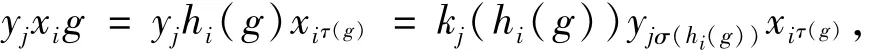
或

由此得

或

又因为K／K′是交换群，且由同态基本定理，H／Ker VH→K≅Im（K／K′）≤K／K′，所以H／Ker VH→K是交换群，于是由引理1得，Ker VH→K≥H′，因而有VH→K（h′）＝K′.

由计算可得

或

由定理1，映射VG→H不依赖于H的陪集代表系的选择，下列定理中所给出的陪集代表的选择方法，对于许多须计算广义转移的问题都是比较方便的.

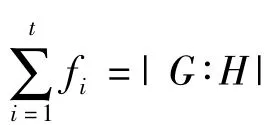
定理3 设G是有限群，P是G的Sylow p-子群.若NG（P）＝CG（P），则G为p-幂零群.

证明 由NG（P）＝CG（P）≥P，知P为交换群.考虑广义转移映射VG→P.若能证明VG→P（G）＝P，则由同态基本定理知Ker VG→P就是G的正规p-补，G为p-幂零群.

事实上，我们可以证明VG→P（P）＝P.设1≠g∈P，由定理2，并注意到P′＝1，有

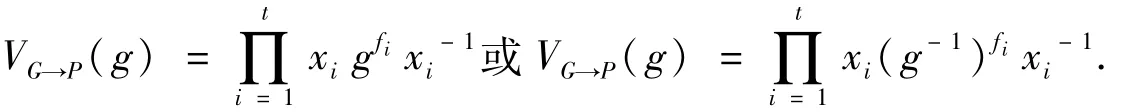
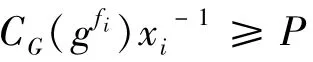
或

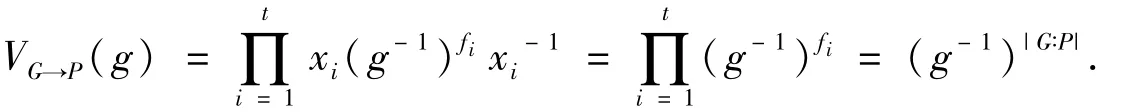
因为（p，｜G：P｜）＝1，由g≠1就得到VG→P（g）≠1.这说明VG→P限制在P上是P到P的单射.由P有限，当然也是满射.因此有VG→P（P）＝P.于是P＝VG→P（P）≤VG→P（G）≤P／P′＝P，从而VG→P（G）＝P.

［1］韦华全，刘秀，杨丽英.广义自同构与有限群结构［J］.四川师范大学学报：自然科学版，2008，31（5）：522-525.

［2］谢芬芳，韦华全，马儇龙.群在集合上的广义作用及广义自同构群［J］.广西师范学院学报：自然科学版，2012，29（2）：17-20.

［3］徐明曜.有限群导引（上册）［M］.北京：科学技术出版社，1999.

［4］张远达.有限群构造（上册）［M］.北京：科学出版社，1982.

［5］HUPPER T B，BLACKBURNN.Endliche cruppen［M］.New York：Springer-Verlag，1967.

［6］王守峰.半群成群的几个充要条件［J］.云南师范大学学报：自然科学学版，2012，32（2）：39-41.

（责任编辑 梁志茂）

Generalized transfer of a finite group

LIU Xiu1，WEI Hua-quan2，3，MA Xuan-long4
（1.School of Mathematics and Statistics，Zhaotong University，Zhaotong 657000，China；2.School of Mathematics，Guangxi Teachers University，Nanning 530023，China；3.College of Mathematics and Information Science，Guangxi University，Nanning 530004，China；4.School of Mathematcal Sciences，Beijng Normal University，Beijng 100875，China）

The concept of generalized substitution expressibility and generalized transfer are given and the Burnsider theory is generalized.

finite group；generalized substitution expressibility；generalized transfer；p-nilpotency

O152.1

：A

：1672-8513（2014）01-0048-04

2013-06-17.

国家自然科学基金（10961007，11161006）；云南省教育厅科学研究基金（2012Y435）.

刘秀（1980-），女，硕士，讲师.主要研究方向：群论.