时空Kriging插值在边坡变形监测中的应用

王建民,张 锦,邓增兵,王燕涛

(1.太原理工大学矿业工程学院,山西太原 030024;2.中煤平朔集团有限公司,山西朔州 036006)

时空Kriging插值在边坡变形监测中的应用

王建民1,张 锦1,邓增兵2,王燕涛2

(1.太原理工大学矿业工程学院,山西太原 030024;2.中煤平朔集团有限公司,山西朔州 036006)

边坡形变监测中的监测点布设受限现场条件,布设位置可能不尽合理且数量有限,监测区域数据处理时需要进行时空插值。将经典的Kriging空间插值进行时空扩展,利用时空一类积和式方法建立了时空变异函数模型;分析了参数与变形的之间的关系;给出了时空插值的计算方法。以平朔露天矿边坡监测为实验对象,将整体时空Kriging插值与单一的Kriging空间插值结果进行对比分析,结果表明,同时兼顾了时间与空间关联性的时空Kriging插值精度有所提高。将监测区进行网格化,初步建立了监测区域的三维动态形变场模型,从整体上分析了边坡的稳定性。

时空插值;Kriging;边坡监测;变异函数

矿山地面灾害种类繁多,其中露天开采工程产生的边坡会给矿山的安全生产带来隐患,实时动态监测边坡的稳定性,研究其变形规律和变形趋势,有利于促进矿山地质灾害环境的一体化管理,对矿区生产建设服务具有重要的现实意义。

近年来,GNSS(global navigation satellite system, GNSS)、测量机器人、多传感器集成系统等高新技术在变形监测中得到应用[1-5],呈现出自动化,高精度的特点,这些先进的监测设备仍需人为布置一定数量的监测点才能发挥其优势。边坡监测点位的选择既受地形条件限制,又受施工作业干扰;另外,贵重的监测设备也不允许无限地增加监测点,从而导致监测点布置缺乏合理性且测点数目相对稀少;有时受其他因素的影响,造成部分监测点的数据缺失或被污染。为了弥补监测点不足、布置不合理以及数据缺失造成的影响,需要应用空间插值方法。变形监测获取的数据是时空数据,如果只进行空间插值,可能忽略了时空相关性,有必要进行时空插值。

空间插值方法主要有几何方法、统计方法、函数方法以及综合方法[6],其中以Kriging为代表的地学统计方法就是对空间随机分布变量的相关性进行定量描述,该方法已应用于众多学科,其可行性和有效性已得到证实。文献[7]应用Kriging方法研究边坡的变形速率,将区域变化量演化为与时间有关的函数,弱化了时空关联性。朱吉祥等运用Kriging插值法研究滑坡危险性区划[8],没有关联前期的观测数据。文献[9]虽然给出了Kriging空间插值的时空扩展方法,但该方法实现简单,其不足之处是计算分隔距离时,仅仅是将时间和空间距离合并计算,没有构建时间变异函数。文献[10-11]应用时空Kriging插值研究了区域变化量的时空分布特征,给出了精度分析,没有与 Kriging空间插值进行对比,体现不出Kriging插值经时空扩展后的优越性。虽然Kriging插值在工程领域得到广泛应用,并得到了较高的评价,但该方法在变形监测数据处理中应用的较少,主要原因是变形监测对于数据的精度要求高,这就决定了插值结果也要达到相应的精度。

本文以平朔露天煤矿边坡监测为研究实验区,从监测数据的特征和规律出发,将单一Kriging空间插值扩展到时空域进行时空Kriging插值,用一类积和式构建时空变异函数,注重的是测点与测点的时空相关性,以2个不同监测周期的监测数据为例,分别进行Kriging空间插值计算,并与整体时空Kriging插值结果进行对比分析。在监测区进行时空插值,建立了时空形变场模型,从整体上分析其变形趋势和稳定性。

1 时空Kriging插值基本原理

Kriging方法是以变异函数理论和结构分析为基础,根据未知样点有限邻域内的若干已知样本点数据,以及变异函数提供的结构信息,对未知样点进行的一种线性无偏最优估计[12]。在实际应用中,常采用抽样的方式获得区域化变量在某个区域内的值。如果采样是一个时空过程,此时的区域变化量将演变成为时空区域变化量[13],时空位置用函数 Z(ha, ta)=Z(x,y,z,t)(ha=f(x,y,z))表示。用普通Kriging进行时空扩展,即

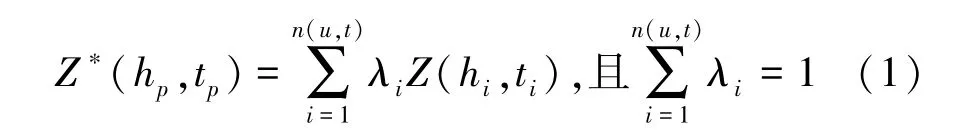
式中,Z∗(hp,tp)为未知点p的估计值;Z(hi,ti)为未知点周围的已知点i的值;λi为第i个已知样本点的权重;n(u,t)为已知样本点对的数目。

1.1 实验变异函数值的估计

为求取权重系数λ,首先根据观测数据计算变异函数γ(hs,ht)的估计值γ∗(hs,ht),即实验变异函数值。用所有已知样本点组成的任意点对计算时空变异函数值,用式(2)进行估算。

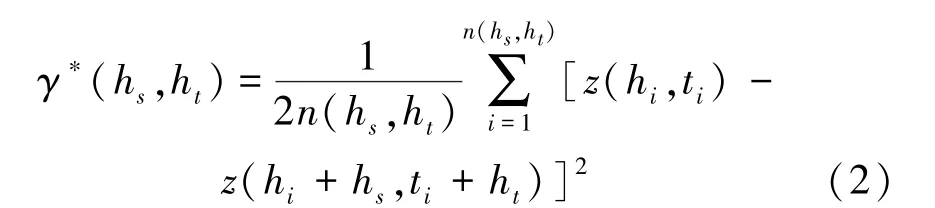
式中,hs,ht为对应的样本空间分隔距离和时间分隔距离;z(hi,ti)为点i的观测值;z(hi+hs,ti+ht)是与z(hi,ti)在空间上相距hs,时间上相距ht的观测值; n(hs,ht)是时空分隔距离为hs和ht的样本点对总数。

取不同的分隔距离(hs,ht),用式(2)可计算出相应的γ∗(hs,ht),以h为横轴,γ∗为坚轴绘制实验变异函数散点图。

1.2 时空变异函数模型

构建变异函数并正确的估计模型参数是时空Kriging插值的核心,常用的有效变异函数模型有指数模型、球形模型、高斯模型[14-15],式(3)是球形模型的一般计算公式。

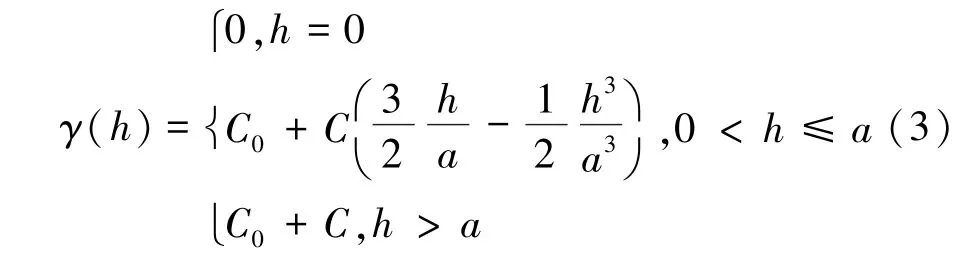
式中,C0为块金值;C0+C为基台值;C为偏基台值;a为变程。

根据变异函数散点图分布特点,选择合适的变异函数模型拟合出变异函数曲线。变异函数曲线反映了一个采样点与其相邻采样点的空间关系。

在变异函数曲线图中有4个相应的参数:块金值(C0)、变程(a)、基台值(C0+C)、偏基台值(C),由这4个参数决定了区域变化量在空间上的变异性。就构造空间变异函数模型而言,技术方法成熟,这里不进行详细说明。在变程a为半径的邻域内,任何两点的数据都是相关的,其相关程度一般随两点的距离增大而减弱。块金系数U(U=C0/(C0+C))是块金值与基台值的比值[16],用于反映变量的空间自相关程度,其值越小表明自相关程度越高。

将空间域扩展到时空域,时空变异函数模型的建立相比空间变异函数复杂。目前,关于时空变异函数模型的研究主要可分为两大类:可分离型和不可分离型[17]。可分离型主要通过将空间变异函数与时间变异函数简单的相乘或相加得到,分割了时间空间的相关信息;而后者虽然构建相对复杂,但更有效地描述了变量的时空变异结构。其中,一类积和式是常用的一种不可分离模型,式(4)是一类积和式时空变异函数模型[13,18]。

其中,γst,γs,γt分别为对应的时空变异函数、空间变异函数和时间变异函数;Cst(0,0),Cs(0),Ct(0)分别为对应的基台值,这3个量可用时空变异函数实验模型(式(2))进行估计;k1,k2,k3是模型中的参数。

时空变异函数γst(hs,ht)的一个主要优点是根据空间变异函数γs(hs)、时间函数γt(ht)和时空台基值Cst(0,0)来确定。Kriging插值要求估计误差的方差最小,用式(4)可以计算出任意2点的时空变异函数值,引入拉格朗日乘除数可求得权重系数λ,许多文献进行过详述[12-13,16],这里不再说明。

1.3 时空插值

空间Kriging只能估计某一时间上未知区域的变形量,估计任意时刻任意位置的变形量,需要用到时空Kriging插值,时空插值的计算步骤如下:

(1)运用式(2)计算实验时空变异函数值,并估计时空台基值Cst(0,0)。

(2)分别设ht=0和hs=0得到对应的γs(hs)和γt(ht),拟合最佳空间变异函数和时间变异函数,得到相应的Cs(0)和Ct(0)。

(3)计算 k1,k2,k3,将参数 Cst(0,0),Cs(0), Ct(0)代入式(4)得到时空变异函数模型。

(4)运用时空变异函数计算观测点的各个权重系数λi,用式(1)计算待估计点的形变Z∗。

2 应用实例

2.1 数据来源

实验区是平朔露天煤矿开采形成的典型边坡,走向方位约为120°,走向长约300 m,海拔约1 300 m,监测区面积约为3.5万m2。研究区域是露天开采后形成的边坡,目前已不再进行露天开采,但是在边坡的一侧下方仍然进行井工开采,如果边坡发生崩塌下滑,可能危害到井工开采,发生安全事故,需要进行监测。监测区沿倾向方向呈阶梯状分布(图1)。为了充分发挥监测点的作用,根据监测区地形特征,在监测区沿走向方向在各个“台阶”上布设了监测点,构成5条监测线,总共有67个监测点。受地形条件限制和施工作业干扰,研究区域上布置的监测点在纵向分布上点间距较小,在横向分布方向上点间距较大,小部分区域的点稀少。

图1 监测点分布Fig.1 Monitoring point arrangement

2.2 实验过程

实验数据由20期的数据组成,因个别监测点数据缺失,总的监测数据量个数小于n=67×20。区域变化量Zk(hi)(i=1,2,…,q(k))(k=1,…,m),m为周期数,m=20。Kriging插值的条件是数据符合正态分布,对监测数据进行正态分布检验(表1,以两期的结果为例),满足Kriging插值的要求。

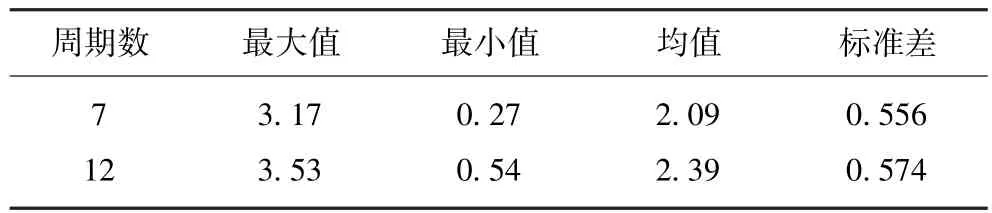
表1 数据统计特征值Table 1 Statistical feature values of data cm

2.2.1 空间插值变异函数

取每期的监测数据用普通Kriging进行独立的空间插值,根据监测点的平均距离和分布,最终确定分隔距离为5 m。在GS+软件的支持下得到实验变异函数值,做实验变异函数的散点图,选择球形模型拟合变异函数曲线,得到对应的变程、台基值、块金值参数,将其代入式(3)可得任意点对的变异函数值。

图2是其中2个周期的空间变异函数结构,对应曲线是经拟合后的变异函数曲线,各自的参数差异列于表2。第12期的变程有所减小,表明监测点较第7期的变异范围减小,趋于稳定;第12期的块金值较小,表明随机性因素影响更小;两期的块金系数都较小,形变有较强的自相关性,可进行空间插值。

图2 2个周期的空间变异函数值的分布及拟合后的变异函数曲线Fig.2 Sample spatial variograms(squares)and fitted variogram models(line)for deformation at two different periods

表2 空间变异函数参数Table 2 Parameters of spatial variograms function

2.2.2 时空插值变异函数

用GS+软件单独进行时间插值(hs=0)和空间插值(ht=0)得到相应的Ct(0)和Cs(0),因GS+不具有时空插值的功能,结合Matlab编程按照前文描述的时空插值的计算步骤,进行时空插值得到时空变异函数的参数(表3),其中时间块金系数小于空间块金系数,表明时间上的相关性强于空间的相关性,时空块金值有所增加,受随机因素的影响增大。

根据表3中的参数值用式(4)求得另3个参数值(k1,k2,k3)。图3(a)是用所有的时空数据利用式(2)建立的时空变异函数的实验模型。图3(b)是用式(4)计算得到的一类积和模型。

表3 时空变异函数参数Table 3 Parameters of space-time variograms function

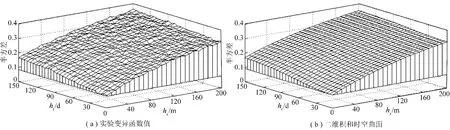
图3 时空变异函数值和二维积和时空曲面Fig.3 Sample space-time variogram surface and 2-D product-sum space-time variogram model

3 插值精度评价

交叉验证法是进行插值的有效性评价的理想方法,基本思想:假设研究的区域内有n个已知点,将测量值Z(θi)(i=1,…,n)暂时从数据中除去,用剩下的测量值建立模型估计除去的测量值 Z∗(θi);将Z(θi)放回到已知数据中,再选其他点进行估计,这样就能得到每个测量值的估计值Z∗(θi)。计算残差dZi=Z∗(θi)-Z(θi),残差值用于计算Z与Z∗一致性的评价指标。经交叉验证后,以Z∗(θi)作为竖轴, Z(θi)作为横轴作误差统计分布。图4(a)和(b)分别是第7期和第12期的空间插值的估计值与实测值的分布和误差统计,图4(c)是时空插值的估计值与实测值的分布和误差统计,从图中可以看出时空插值的点距离直线相对集中一些,而且小误差更多,说明时空插值精度有所提高。

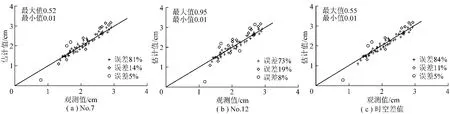
图4 2个不同周期仅空间插值的估计值与实测值散点图和时空插值的散点Fig.4 The bivariate distribution of predicted against actual values with only space Kriging for No.7 and No.12 and the bivariate distribution of predicted against actual values with space-time Kriging

根据残差计算结果,用残差由式(5)计算均方根预测误差(RMSE),式(6)计算平均误差(ME)作为检验标准衡量插值效果的有效性,检验标准值越小则估值结果越准确,插值效果越好,预测值就越接近它们的真实值;平均误差趋于0认为估计是无偏的;式(7)计算判定系数R2,R2由残差平方和总体平方和两部分组成,其值越接近1,表明线形相关程度越高。

式中,Z∗(θ)为估计值;Z(θ)为在相同点的观测值;n为估计点的数量。

将空间插值和时空插值交叉验证的评价指标列于表4,从表中可以看出空间插值和时空插值都具有较强的线形相关性,时空插值的预测精度有所提高,其中时空插值的RMSE比空间插值分别提高38.8%和47.6%;时空插值的ME比空间插值分别提高54%和58%。

将监测区域进行网格化,在格网点上对同期数据分别进行空间插值和时空插值,建立三维时空形变场模型(图5)。从模型中可以看出,接近边坡底部位置变形较大,边坡上方的形变较小,两种插值结果变化不明显;边坡下方区域时空插值比空间插值变形大,由于时空插值使用了时空数据,说明该区域长期以来变形较大。

表4 精度评价指标Table 4 Precision evaluation

图5 同期空间插值和时空插值的三维形变场Fig.5 Three-dimensional deformation field at the same period spatial interpolation and space-time interpolation

4 结 语

考虑边坡变形的区域性,将Kriging空间插值扩展到时空域,依据实验区的监测点分布特征和监测周期,选择合适的时空分隔距离,构建了时空变异函数模型,给出了相应的算法,实现了时空联合插值。经过实例验证,时空Kriging比单粹Kriging空间插值精度得到提高。在监测区域进行时空插值计算,建立了监测区域的三维形变场模型,从整体上预测了边坡区域的稳定性和形变趋势。

时空Kriging插值的不足之处是计算量较大,在选择变异函数模型时还需要人工干预。今后需进一步研究自适应变异函数模型,优化算法提高多周期累积数据计算效率,实现变形观测数据处理和图形输出的自动化。

[1] Zhao Y,Qian Q.A new type of automatic monitoring system of static and dynamic[J].Procedia Engineering,2012,43:387-392.

[2] Xiao J,Zhang J.Analysis and application of automatic deformation monitoring data for buildings and structures of mining area[J].Transactions of Nonferrous Metals Society of China,2011,21(S3): 516-522.

[3] 张 锦.矿山地面灾害精准监测地学传感网系统[J].地球信息科学学报,2012,14(6):681-685.

Zhang Jin.The geosensor networks for precise monitoring of mine ground disaster[J].Journal of Geo-Infromation Science,2012, 14(6):681-685.

[4] Peci L M,Berrocoso M,Paez R.Automatic system for monitoring ground deformation on the Deception Island volcano[J].Computers and Geosciences,2012,48:126-133.

[5] 孟 磊,丁恩杰,吴立新.基于矿山物联网的矿井突水感知关键技术研究[J].煤炭学报,2013,38(8):1398-1402.

Meng Lei,Ding Enjie,Wu Lixin.Research on key technologies of water inrush perception based on mine IoT[J].Journal of China Coal Society,2013,38(8):1398-1402.

[6] 李 新,程国栋,卢 玲.空间内插方法比较[J].地球科学进展,2000,15(3):260-265.

Li Xin,Cheng Guodong,Lu Ling.Comparison of spatial interpolation methords[J].Advance in Earth Sciences,2000,15(3):260-265.

[7] 刘志平,何秀凤,张淑辉.多测度加权克里金法在高边坡变形稳定性分析中的应用[J].水利学报,2009,40(6):709-716.

Liu Zhiping,He Xiufeng,Zhang Shuhui.Multi-distance measures weighted Kriging method for deformation stability analysis of steep slopes[J].Joural of Hydraulic Engineering,2009,40(6):709-716.

[8] 朱吉祥,张礼中,周小元,等.Kriging法在区域滑坡危险性评价中的应用[J].水文地质工程地质,2012,39(3):114-118.

Zhu Jixiang,Zhang Lizhong,Zhou Xiaoyuan,et al.Application of Kriging to the assessment of regional landslide hazards[J].Hydrogeology&Engineering Geology,2012,39(3):114-118.

[9] 徐爱萍,胡 力,舒 红.空间克里金插值的时空扩展与实现[J].计算机应用,2011,31(1):273-276.

Xu Aiping,Hu Li,Shu Hong.Extension and implementation from spatial-only to spatio temporal Kriging interpolation[J].Journal of Computer Applications,2011,31(1):273-276.

[10] 李 莎,舒 红,徐正全.利用SKKriging进行气温插值研究[J].武汉大学学报信息科学版,2012,37(2):237-240.

Li Sha,Shu Hong,Xu Zhengquan.Interpolation of temperature based on spatioal-temporal Kriging[J].Geomatice and Information Science of Wuhan University,2012,37(2):237-240.

[11] Kyriakidis P C,Journel A G.Geostatistical space-time models:A review[J].Mathematical Geology,1999,31(6):651-684.

[12] 王建民.基于Kriging下的移动曲面拟合法研究[J].测绘科学, 2012,37(4):160-162.

Wang Jianmin.Moving surface fitting models based on Kriging method[J].Science of Surveying and Mapping,2012,37(4): 160-162.

[13] Gething P W.A local space-time Kriging approach applied to a national outpatient malaria data set[J].Computer&Geosciences, 2007,33(10):1337-1350.

[14] 张仁铎.空间变异理论及应用[M].北京:科学出版社,2005: 20-26.

[15] Hamid A S.Application and evaluation of Kriging and cokriging methods on groundwater depth mapping[J].Environ Monit Assess,2008,138(1-3):357-368.

[16] 吴学文,晏路明.普通Kriging法的参数设置及变异函数模型选择方法[J].地球信息科学学报,2007,9(3):104-109.

Wu Xuewen,Yan Luming.Setting parameters and choosing optimum semivariogram models of ordinaty Kriging interpolation[J].Journal of Geo-Infromation Science,2007,9(3):104-109.

[17] Cesare L D,Myers D E,Posa D.Estimating and modeling space time correlation structures[J].Statistics&Probability Letters, 2001,51(1):9-14.

[18] Jost G,Heuvelink G B M,Papritzc A.Analysing the space-time distribution of soil water storage of a forest ecosystem using spatio-temporal Kriging[J].Geoderma,2005,128(3):258-273.

Slope deformation analyses with space-time Kriging interpolation method

WANG Jian-min1,ZHANG Jin1,DENG Zeng-bing2,WANG Yan-tao2

(1.College of Mining Technology,Taiyuan University of Technology,Taiyuan 030024,China;2.China Coal Pingshuo Group Co.,Ltd.,Shuozhou 036006, China)

Slope deformation analyses based on monitoring points are unscientific because of limited monitoring points and unreasonable layout.Therefore,the interpolation of deformation information from monitoring points is very necessary.In this paper,the space-time Kriging interpolation was used to analysis slope deformation in Pingshuo Open-pit Mine instead of classic Kriging interpolation.The space-time variograms function using the space-time of 2D productsum method was established,and the relationship between the main parameters of the model and the deformation was analyzed.The results show that the accuracy of space-time Kriging interpolation is satisfactory when the temporal-spatial relevance is considered.Accordingly,the dynamic deformation models were established based on the grid points of the monitoring area.The models are important for the analysis of slope stability from the regional scale.

space-time interpolation;Kriging;slope monitoring;variogram function

TD824

A

0253-9993(2014)05-0874-06

王建民,张 锦,邓增兵,等.时空Kriging插值在边坡变形监测中的应用[J].煤炭学报,2014,39(5):874-879.

10.13225/j.cnki.jccs.2014.0282

Wang Jianmin,Zhang Jin,Deng Zengbing,et al.Slope deformation analyses with space-time Kriging interpolation method[J].Journal of China Coal Society,2014,39(5):874-879.doi:10.13225/j.cnki.jccs.2014.0282

2014-03-09 责任编辑:王婉洁

国家高技术研究发展计划(863)资助项目(2013AA122301);国家自然科学基金资助项目(41371373);山西省软科学基金资助项目(2013041060-02)

王建民(1976—),男,内蒙古乌兰察布人,讲师。E-mail:8844.4321@163.com