基于混合指标类型的评价方法研究与应用

荣丽丽，刘培德

（1．山东广播电视大学计算机与通信学院，山东 济南 250101；2．山东财经大学管理科学与工程学院，山东 济南 250014）

基于混合指标类型的评价方法研究与应用

荣丽丽1，刘培德2

（1．山东广播电视大学计算机与通信学院，山东 济南 250101；2．山东财经大学管理科学与工程学院，山东 济南 250014）

为增强决策的科学性，优化混合指标类型的评价方法，本文综合考虑了评价体系中的定性和定量指标，采用AHP方法确定指标的主观权重，离差最大化方法确定指标的客观权重，乘法合成法确定指标的组合权重。通过基于混合指标的TOPSIS方法排序，确定方案的优劣。案例分析表明，该方法在实际应用中是有效的。

评价；混合指标；TOPSIS

在社会经济的各个领域中，利用模糊数学解决了许多大型的决策优化问题。郝庆龙等［1］将其应用于液化天然气终端港址的比较与选择；侯彩虹等［2］应用于海关企业诚信评价；简迎辉等［3］应用于水利工程总承包交易模式选择；郭璘等［4］用于公共交通领域；邓晓衡等［5］用于人防预案评估；王中兴等［6］给出了一种区间直觉模糊数的排序方法，并将此排序方法应用到多属性决策当中；吴莉等［7］建立了一种基于区间直觉模糊集模型的群决策途径，并根据群决策结果评判专家的水平。但是很多数学模型形式复杂，使得决策者难以驾驭。本文将区间模糊数、三角模糊数应用于混合指标类型的评价和决策过程中，使得评价指标实现了量化，具有可操作性。

农业是国民经济和社会发展的基础，社会主义新农村建设是我国现阶段一项复杂的系统工程，建立一套科学、全面、合理、可操作的社会主义新农村评价方法具有重要意义。至今为止，很多专家及不同的组织对我国社会主义新农村建设提出过不同的评价方法，马晓燕等［8］提出了基于集对分析的社会主义新农村建设评价模型；薛芬菊等［9］提出了基于聚类分析方法的甘肃民族地区新农村发展水平评价模型；朱春江［10］提出了综合加权和神经网络相结合的社会主义新农村建设评价方法，并以连云港新农村建设评价为例给出了实证研究；王汝发等［11］提出了基于模糊分析的社会主义新农村建设评价模型。

随着我国新农村建设的不断深入，现有的评价指标体系和评价方法的缺点也日显凸出，一方面，评价指标体系的全面性和系统性有待于进一步完善；另一方面，没有考虑评价指标的模糊性，特别是同时考虑定性指标和定量指标情况。本文建立的社会主义新农村建设评价模型，采用了新的评价方法，即考虑评价指标同时存在定性和定量的情况。

1 基于混合指标类型的评价方法

在评价和决策过程中，评价指标存在模糊性，不可能都用定量的实数表示。因此，对某些定性指标可以采用语言变量表示，对某些指标可能采用区间数表达较为方便。本文考虑评价指标为实数、区间数、三角模糊数以及语言变量等情况下的评价方法。

1.1 语言变量转化为模糊数

1.1.1 语言变量集

设语言评价集S＝（s0，s1，…，sl－1）应由奇数个元素组成，即l应为奇数。在实用中l一般取5，7，9等。其表示为

S＝（s0，s1，s2，s3，s4）＝（差，较差，中，好，很好）。

S＝（s0，s1，s2，s3，s4，s5，s6）＝（很差，差，中下，中，中上，好，很好）。

S＝（s0，s1，s2，s3，s4，s5，s6，s7，s8）＝（极差，很差，差，中下，中，中上，好，很好，极好）。

1.1.2 语言变量转化为区间数

设语言评价集中的语言词si用区间数表示为：［ai，bi］，则有［12］

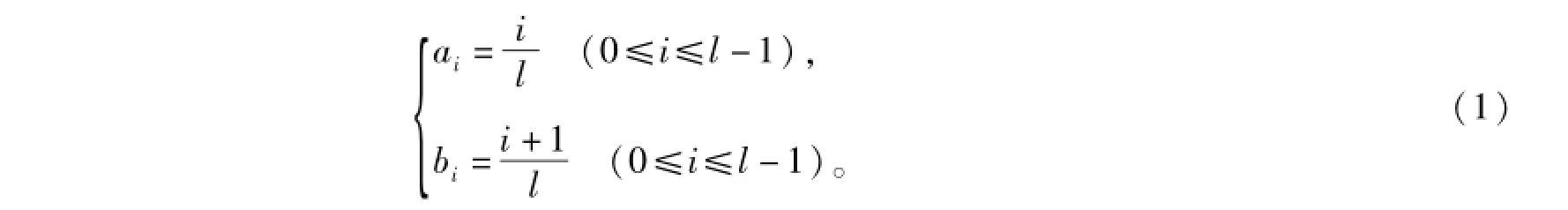
如当l＝5时，语言变量集所有语言词用区间数表示为

s0＝［0，0.2］，s1＝［0.2，0.4］，s2＝［0.4，0.6］，s3＝［0.6，0.8］，s4＝［0.8，1.0］。

1.1.3 语言变量与三角模糊数的转化

设自然语言的三角模糊数表示为：si＝（ai，bi，ci），则有

由此，可以得到5时的语言变量集与三角模糊数的对应关系（已规范化），见表1。

表1 五级语言评价集转化为三角模糊数Table 1 Conversion of 5 linguistic evaluation sets to triangle fuzzy numbers

1.2 不同类型评价数据的规范化

对语言变量，直接转化为三角模糊数即可。

1.2.1 精确数的规范方法

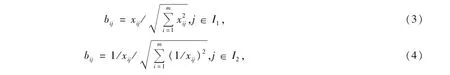
I1为效益型指标，I2为成本型指标（以下同）。

1.2.2 区间模糊数的规范化方法

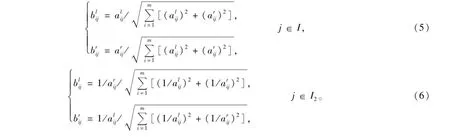
1.2.3 三角模糊数的规范化方法

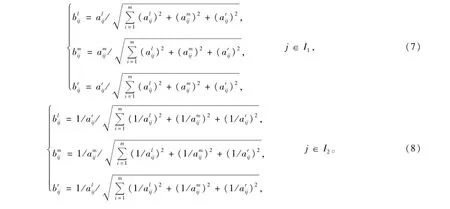
1.3 不同类型评价数据的距离

1.3.1 实数型变量之间的距离

设a，b是两个实数，则实数a，b之间的距离定义为

1.3.2 区间数之间的距离

设a＝（al，ar）和b＝（bl，br）是两个区间数，则区间数a，b之间的距离定义为

1.3.3 三角模糊数之间的距离

设a＝（al，am，ar）和b＝（bl，bm，br）是两个三角模糊数，则三角模糊数a，b之间的距离定义为

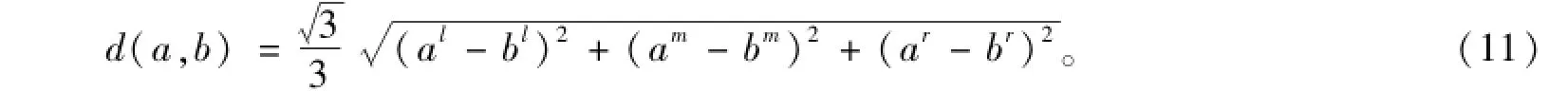
1.4 基于离差最大化的客观权重确定方法

由于评价属性权重未知，而属性权重的不同将会引起决策方案排序的不同。通常情况下，如果得到的指标属性cj下的属性值rij（j＝1，2，…，n）有较小的离差，说明该属性对方案决策起到的作用较弱；如果得到的决策属性cj下的属性值rij＝（j＝1，2，…，n）有较大的离差，则说明该属性对方案决策起到的作用较强（属性值rij是规范化后决策数据）。

综上所述，在对决策方案进行排序的过程中，将属性值差异大的方案赋予较大的权重，将属性差异小的方案赋予较小的权重。其中，差异用两个属性值之间的距离表示。

构建如下优化模型

构造Lagrange乘子函数，有

求解该模型，可以得到

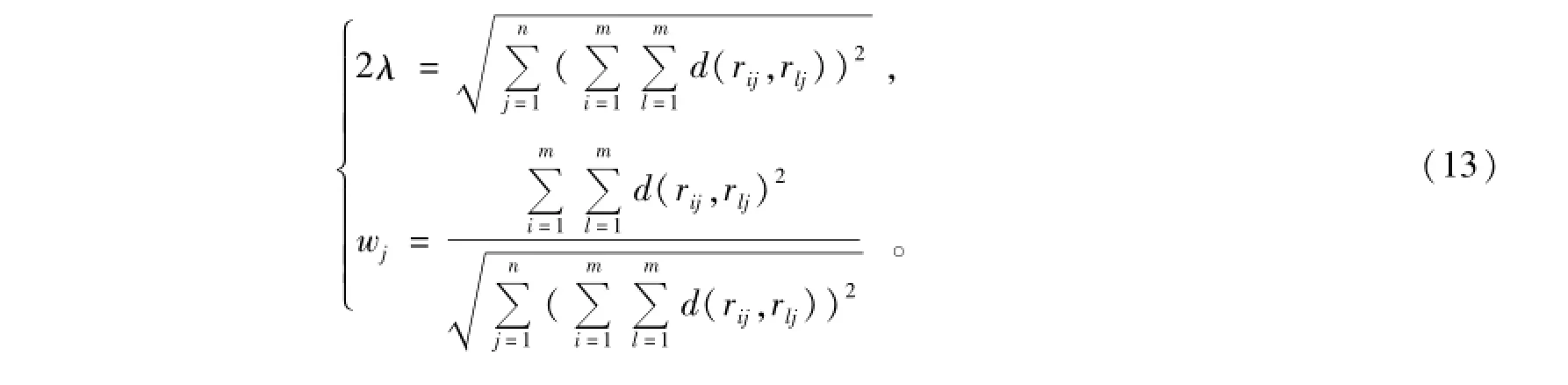
对指标权重归一化后，得到

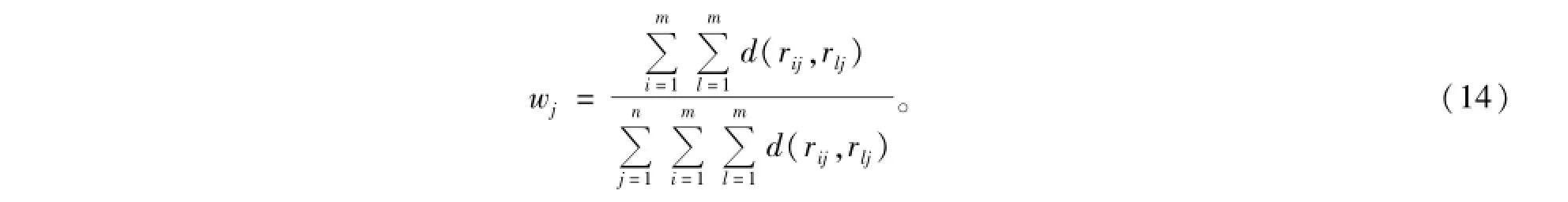
1.5 组合权重的确定方法

主观权重存在着专家经验背景丰富的优势，也同时存在主观偏好影响科学决策的劣势。为了减少评价体系中的主观随意性，引入客观数据，达到主客观统一，从而提高决策的科学性与准确性。

1.6 基于混合指标值TOPSIS方法的评价模型

TOPSIS（Technique for order performance by similarity to ideal solution）也称为逼近理想点法，用以评价决策方案的相对优劣。此方法需要先计算各项指标的正理想解（各指标属性达到最满意的解）和负理想解（各指标属性达到最不满意的解），然后将原方案与正负理想解进行比较，通过计算它们之间的距离评价方案的优劣。

通常TOPSIS方法只适合属性值为实数的情况，本节我们将扩展TOPSIS方法以适合混合数据类型，其步骤如下。

1.6.1 计算虚拟理想解和负理想解

（i）如果指标j为实数型，则有

（ii）如果指标j为区间数，则有

（iii）如果指标j为三角模糊数，则有

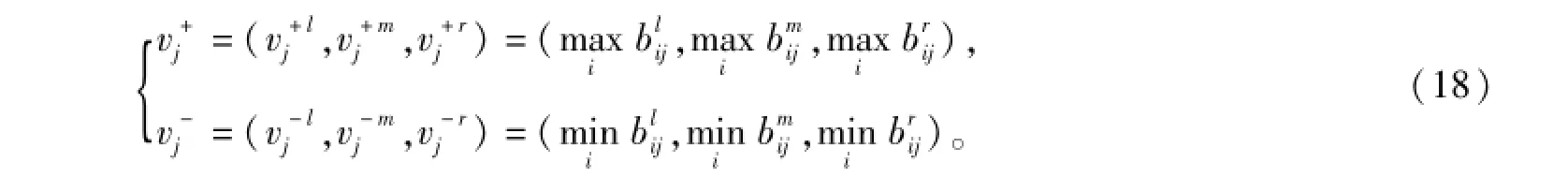
1.6.2 计算各方案ai与虚拟理想方案v＋和虚拟负理想方案v－的广义加权距离

计算公式为

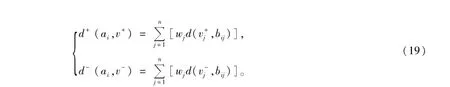
1.6.3 计算各方案的相对贴近度

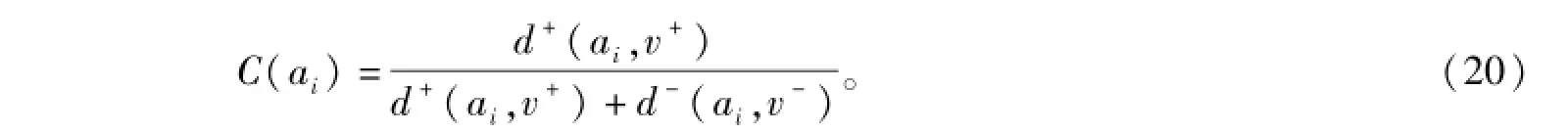
1.6.4 方案优劣排序

计算出相对贴近度C（ai），根据数值大小，进行排序。C（ai）数值越小，方案越优；否则，方案越劣。

2 应用实例

为了深入地了解山东省新农村建设的情况，课题组深入到潍坊、枣庄、烟台、滨州和聊城等地进行走访。调查村庄132个，走访乡镇24个，访谈对象为村民、村支部书记和分管副乡长。通过调研，获得了详实的调查数据，这些数据为构建基于混合指标类型的社会主义新农村评价体系提供了依据。

2.1 指标体系的建立

根据社会主义新农村建设的具体要求，首先提取了相关的指标，主要包括生产发展、生活富裕、乡风文明、村容整洁和管理民主。

分别采用了深度访谈法与网上问卷调查的方法，向中国26位资深专家及教授进行调查咨询。基于调查结果，本文构建出社会主义新农村建设评价指标体系，详见表2。

表2 社会主义新农村建设评价指标体系Table 2 Evaluation index system for the construction of new socialist country

2.2 指标主观权重的确定

指标主观权重的确定采用层次分析法（Analytic Hierarchy Process，AHP），此方法由美国匹兹堡大学的T．L．Saaty教授率先提出，用于解决定性与定量相结合的决策分析。其核心是将决策目标层层分解，逐级构建判断矩阵，最后加权递归求得权重。

采用AHP方法，通过对12位专家的调查，构造如下的判断矩阵、特征向量及一致性检查。

（1）判断矩阵A-A1

CR＝0．037 9＜0．10

（2）判断矩阵A1-B

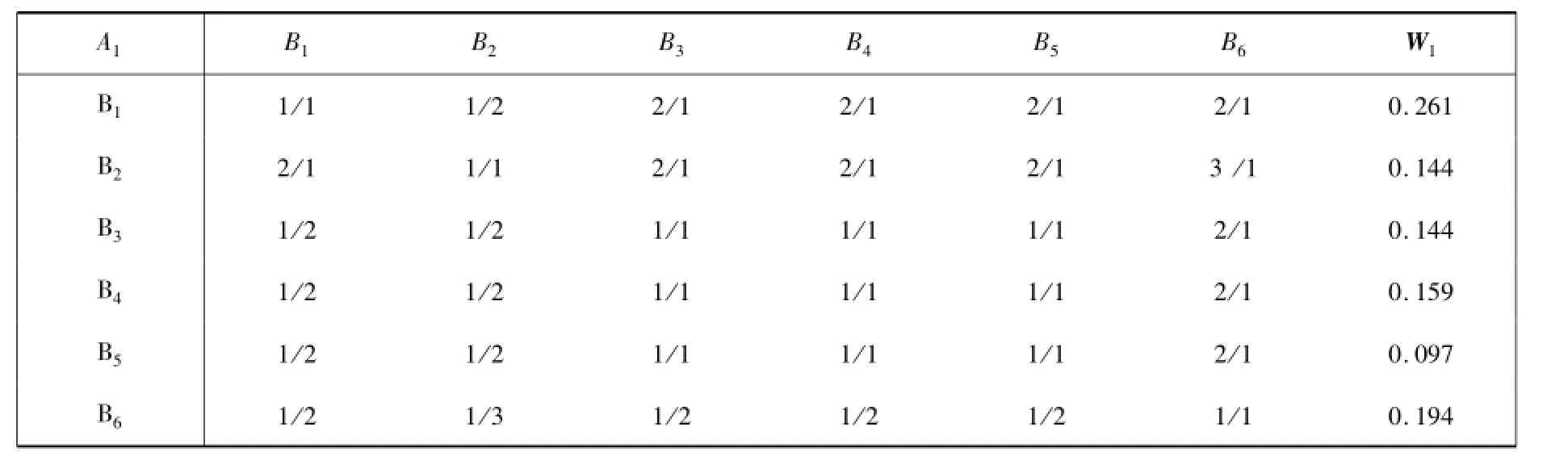
CR＝0．043 1＜0．10

（3）判断矩阵A2-B

CR＝0．015 5＜0．10

（4）判断矩阵A3-B

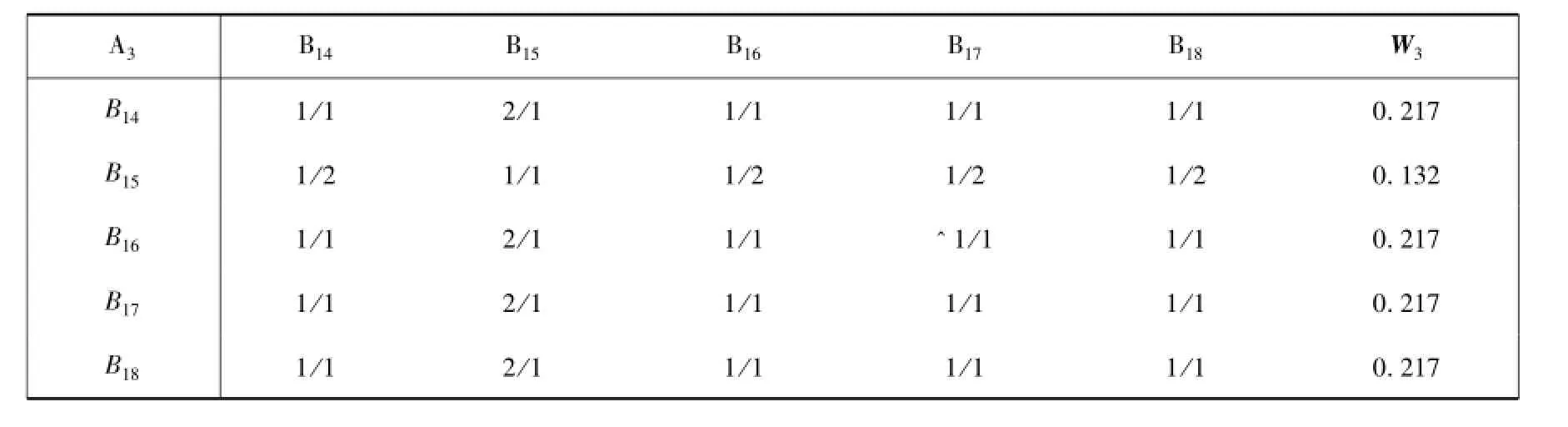
CR＝0.008 2＜0.10

（5）判断矩阵A4-B

CR＝0.001 7＜0.10

（6）判断矩阵A5-B

CR＝0．00＜0．10

根据W及W1，W2，W3，W4，W5，求层次总排序权重。

层次总排序的随机一致性比例为CR＝0.0372＜0.1，故层次总排序有效。

2.3 基于离差最大化确定权重属性

为了确定指标的客观权重，课题组通过调研，获得了详实的调查数据。为便于对比分析，我们对资料进行整理，形成了潍坊市5个乡镇的新农村评价数据，见表3。

在表3中，对B18（人民群众对社会治安的满意度）和B25（村民对村务公开的满意度）采用语言评价，语言变量集采用S＝（s0，s1，s3，s4）（很不满意，不满意，一般，满意，很满意）5级语言变量集。

设a1＝临朐九山镇，a2＝昌乐乔官镇，a3＝青州王坟镇，a4＝寿光营里镇，a5＝坊子区坊子镇。

步骤如下。

2.3.1 对决策数据规范化

B8和B13为成本型指标，其他为收益型指标。另外，将B18指标的语言变量转化成区间数，将B25指标的语言变量转化成三角模糊数。设归一化后的矩阵为X，则有

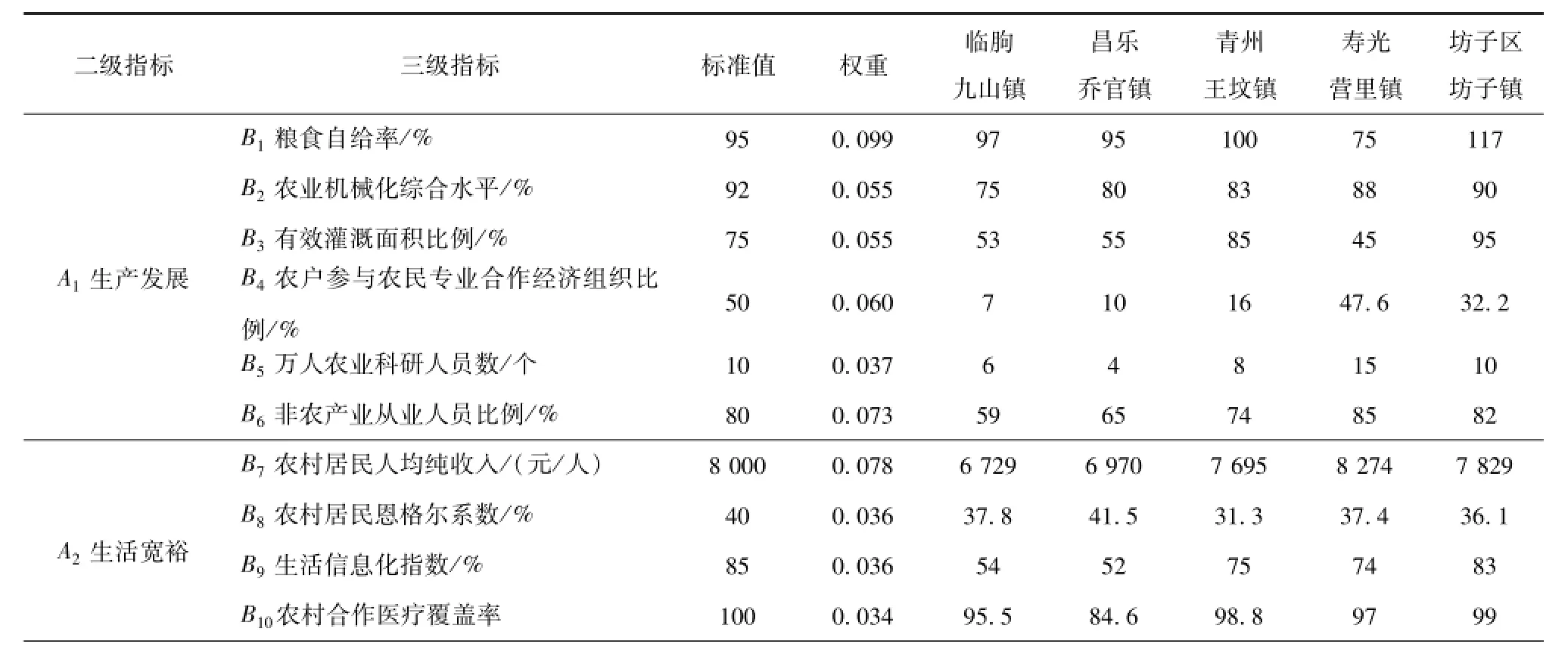
表3 山东省潍坊市社会主义新农村建设评价指标数据表Table 3 Data table of the evaluation index for the construction of new socialist country in Weifang of Shandong

其中，我们改行为乡镇，列为指标，则矩阵为5×25。

2.3.2 基于离差最大化方法确定指标权重W

2.3.2 求组合权重

根据AHP方法确定权重为主观权重，用离差最大化求得权重为客观权重，组合权重采用乘积方法，得到的组合权重为ω，则有

2.4 利用TOPSIS方法对方案进行排序

2.4.1 求加权矩阵R（R＝X*ωT）

2.4.2 计算正负理想解R＋，R－

2.4.3 计算各方案与正负理想方案之间的距离

2.4.4 计算相对接近度

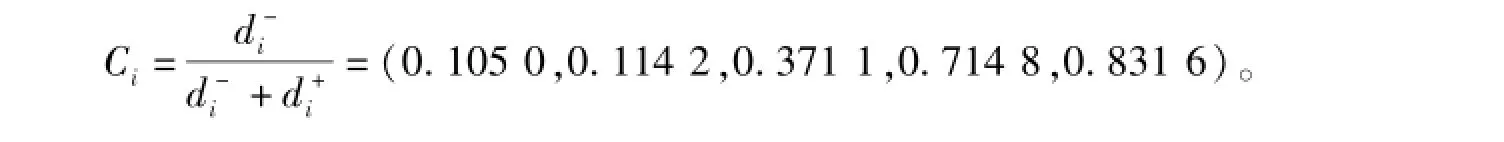
2.4.5 对方案进行排序

根据相对接近度大小对方案进行排序。可以得到

a5＞a4＞a3＞a2＞a1

即坊子区坊子镇的新农村建设最好，临朐县九山镇的建设最差。

3 结论

本研究将混合指标类型评价方法进行优化，从只处理单一的实数、区间数、三角模糊数或语言变量，扩展到混合数据类型，将定性分析和定量分析的优势结合起来。研究结果表明，该方法便于操作，易于推广使用。今后，在研究广度上，需要进一步扩大实证范围；在研究深度上，需要考虑不同规范化方法对混合指标类型排序产生的影响。另外，基于混合指标类型的评价体系是动态变化的，因此其评价指标需要不断进行调整，评价方法需要不断进行优化。

［1］郝庆龙，戴冉．基于模糊评价的大连液化天然气终端港址比选［J］．大连海事大学学报：自然科学版，2013，39（3）：103－106．

［2］侯彩虹，李红霞．基于灰色模糊决策法的海关企业诚信评价［J］．统计与决策，2012（17）：175－177．

［3］简迎辉，张勇．基于直觉模糊IFWA算子的水利工程总承包交易模式选择研究［J］．中国农村水利水电．2012（2）：142－145．

［4］郭璘，陈琳莉，王茹．基于模糊综合评判的多源公交动态数据融合［J］．计算机工程，2012，38（12）：169－171．

［5］邓晓衡，刘雪芹，陈志刚．基于模糊综合评判的人防预案评估模型［J］．计算机工程，2011，37（17）：252－255．

［6］王中兴，唐芝兰，牛利利．基于相对优势度的区间直觉模糊多属性决策方法［J］．山东大学学报：理学版，2012，47（9）：92－97．

［7］吴莉，徐肖震．基于区间直觉判断矩阵的群决策及逆判方法［J］．重庆文理学院学报：自然科学版，2012，31（5）：28－32．

［8］马晓燕，国忠金，田力，等．社会主义新农村建设评价指标体系的集对分析模型［J］．数学的实践与认识，2010，40（14）：9－15．

［9］薛芬菊，张艳荣．基于聚类分析法对甘肃民族地区新农村建设评价研究［J］．黑龙江农业科学，2011（10）：106－108．

［10］朱春江．基于神经网络理论的新农村建设评价研究［J］．江苏农业科学，2011（1）：466－468．

［11］王汝发，韩文春．基于模糊分析的社会主义新农村建设评价模型［J］．中国发展，2012，12（1）：51－55．

［12］刘培德．基于模糊多属性决策的企业信息化水平评价方法与应用研究［D］．北京：北京交通大学，2009．

Research and application of evaluation method based on the hybrid indexes type

RONG Li-Ii1，LIU Pei-de2
（1．School of Computer and Communications，Shandong TV University，Jinan 250101，China；2．School of Management Science and Engineering，Shandong University of Finance and Economics，Jinan 250014，China）

This paper add resses qualitative and quantitative indexes of a com prehensive evaluation method to enhance the scientificity of a decision and optimize the evaluation methods of hybrid index type．We determine their subjective weights with AHP，their objective weights with deviation maximization，and their portfolio weights with multiplication synthesis．We determine the positives and negatives of the approach through hybrid indexes based TOPSIS sorting．Case study shows that the approach is effective in practical applications．

evaluation；hybrid indexes；TOPSIS

O159；C934

A

1002-4026（2014）03-0093-10

10.3976／j.issn.1002－4026.2014.03.018

2014-04-15

国家自然科学基金（71271124）；山东省自然科学基金（ZR2011FM036）

荣丽丽（1982－），女，硕士，研究方向为决策理论与优化方法。Email：ronglili＠126．com