基于时间序列模型的轨道质量指数预测研究

宋博洋

（北京交通大学交通运输学院，北京 100044）

基于时间序列模型的轨道质量指数预测研究

宋博洋

（北京交通大学交通运输学院，北京 100044）

轨道质量指数（TQI）是反映区段轨道整体不平顺的一项重要指标，是一个具有随机性特征的时间序列。本文用灰色系统理论分析TQI序列与各单项指标间的关联度并预测某区段下一次检查的数值；运用ARMA模型对200 m单元区段的TQI序列数据进行研究，分析其变化趋势并对未来一段时间的TQI进行预测。算例分析表明，两个模型的预测精度有所提高，相对误差小于5%。

时间序列；ARMA模型；关联度；修正GM（1，1）；轨道质量指数

1 引言

随着我国铁路网规模的不断扩大，铁路运输在促进国民经济发展中起着越来越重要的作用。同时，铁路养护维修工作也变得更为重要和复杂［1］。铁路行车安全是铁路运输工作的基本要求，而铁路轨道不平顺是使列车产生振动的主要原因，会对列车的行车质量产生重大影响［2］。准确掌握轨道状态的变化规律，制定合理的养护维修计划，是解决行车安全问题的重要内容。因此，铁路工务部门提出了以轨道状态为基础的“状态修”。

轨道质量指数（track quality index，TQI）是反映区轨道整体平顺程度的一项重要指标，是一个具有随机特性的时间序列。徐伟昌［3］提出一种基于累计通过总重的线性模型进行预测，其基本公式为

其中，TQI0为初始时刻的轨道质量指数，K为线路的劣化速率，T为累计通过总重。

此模型的预测结果可以基本反映短期TQI的变化趋势，但是影响轨道的劣化因素不仅包括累计通过总重，而且跟所处的地理位置、温度、降水以及测量误差等因素相关，因此用直线拟合可能会产生比较大的偏差。

本文针对上述线性模型存在的问题，提出用灰色系统理论对TQI序列进行相关性分析和短期预测，用时间序列分析模型ARMA对每个200 m单元区段分别建模进行中长期预测，对制定铁路线路的维修计划具有一定的指导意义。

2 灰色分析及预测

灰色预测是针对介于白色系统和黑色系统之间的灰色系统的预测，系统内一部分信息是已知的，另一部分信息是未知的，且内部各因素之间具有不确定的关系。

2.1 灰色关联分析

灰色关联分析的基本思想是根据序列曲线集合形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度就越大，反之就越小［4］。

设x0＝（x0（1），x0（2），…，x0（n））为某一系统的行为特征序列，且

为相关性因素。记

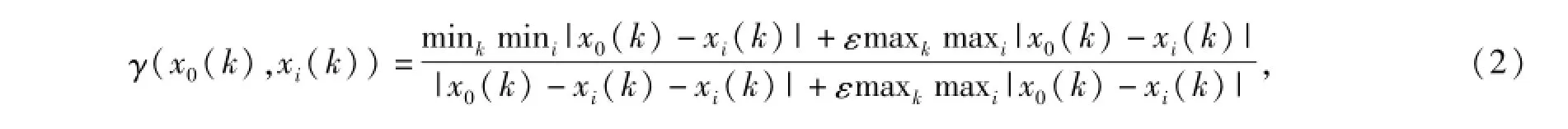
轨道质量指数TQI是7项单项指标的标准差之和，通过进行灰色关系度分析，可以找出影响TQI值的最主要因素，为采取有预防性的措施提供理论基础。

2.2 改进灰色GM（1，1）模型

灰色GM（1，1）模型主要是针对指数递增序列进行预测的，但实际上大部分时间序列数据不具有指数递增的趋势，此时灰色模型的预测精度就会降低。因此需要对原始模型进行改进，使之能够扩大应用领域。本文提出了利用残差对原始模型进行改进的方法，试验证明这种改进后的模型可以在一定程度提高预测的精度，预测结果对实际工作具有指导意义。

设数据的原始序列为：X0＝（x0（1），x0（2），…，x0（n））（x是TQI时序检测数据），根据灰色系统理论，灰色预测模型GM（1，1）的基本形式为［3－4］：

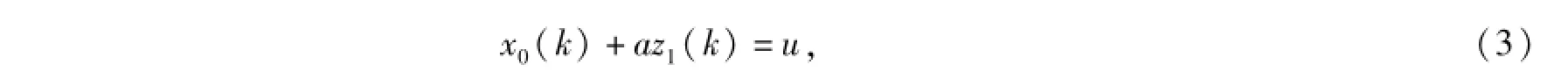
模型的时间响应序列为

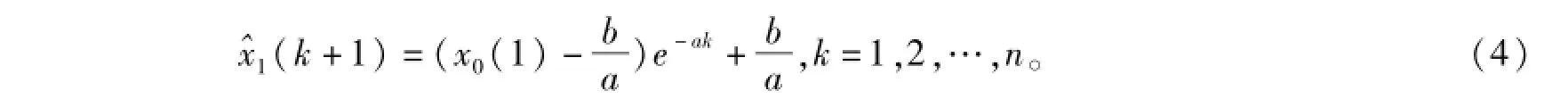
当原始序列的波动性比较大时，GM（1，1）模型的精度比较低，此时需要对原始模型进行修正改进，以提高精度。

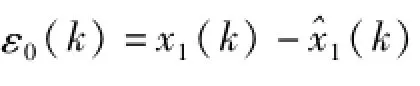
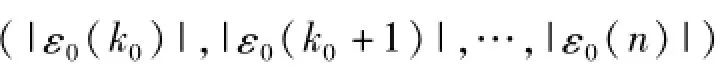
对ε0应用GM（1，1）模型进行计算，得其模拟序列

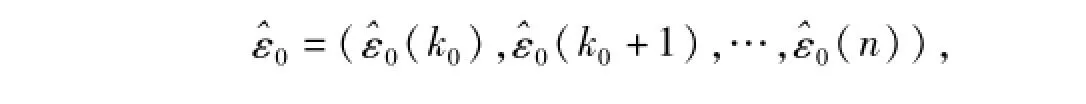
用模拟得到的序列ε0修正，称修正后的时间响应式

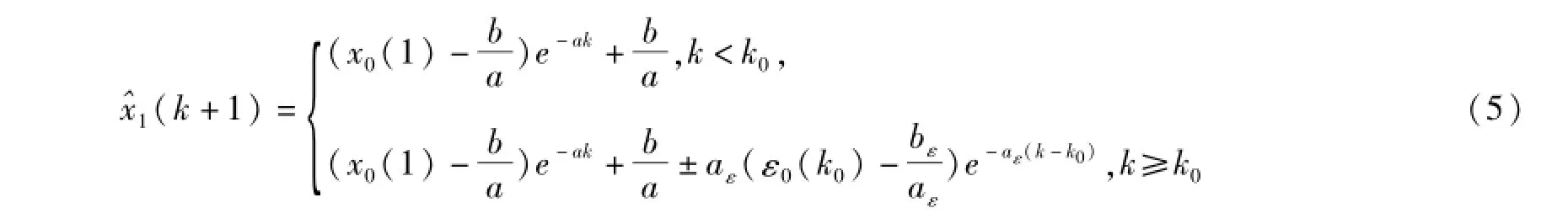
为残差修正GM（1，1）模型。

3 ARMA模型及改进

3.1 ARMA模型及其求解

ARMA模型（auto-regressivemoving averagemodel）又称自回归移动平均模型，是一种精度较高的时序短期预测模型，其基本思想是：某些时间序列是依赖于时间t的一组随机变量，构成该时序的单个序列值虽然具有不确定性，但整个序列的变化却有一定的规律性，可以用相关的数学模型近似描述。通过对该数学模型的分析研究，更本质地认识时间序列的结构与特征，达到最小方差意义下的最优预测。ARMA（p，q）的一般形式为［7－8］：

其中，p，q分别表示滞后的阶数，εt是白噪声序列。

由已有的研究可知，轨道质量指数TQI随时间变化的序列｛TQIt｝不是一个平稳的时间序列，在一定程度上具有指数变化的特征。本文取经过差分后的序列作为研究对象。｛TQIt｝的一阶差分序列用｛TQIt1｝表示，其计算公式为

同理，可以计算TQI的二阶、三阶差分序列。具体的差分阶次由差分后的序列是否平稳所决定。这样经过d阶差分变为平稳序列后，对其进行建模预测，得到结果后再反向推导出原始序列的预测值。

确定模型的阶数，即确定p和q。一般有3种方法，即偏、自相关函数法、FPE准则和AIC及BIC准则。本文采用第一种方法确定p和q的取值，并结合TQI的变化规律，在此方法上提出改进。

3.2 模型的改进

轨道质量指数序列是一组沿时间方向上下波动的数据，数据本身的单调性不明显，此时ARMA模型的适用性会降低，进而影响预测的精度。TQI时间序列的波动性是由趋势项和随机噪声两项叠加而成的，基于此本文采用灰色系统理论中的叠加处理手段对ARMA模型进行了改进，尽量消除TQI波动性对模型预测精度的影响。具体的实现过程如下

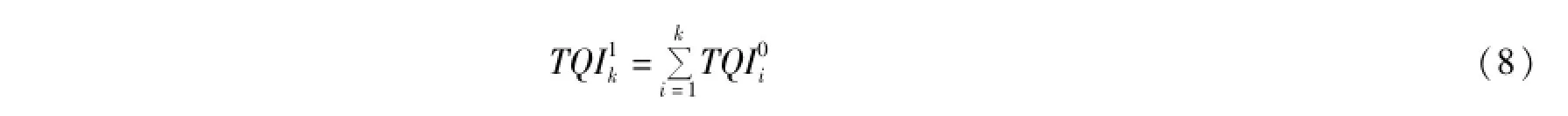
将经过处理后的数据序列建立模型进行预测，步骤如3.1，预测得到的结果为

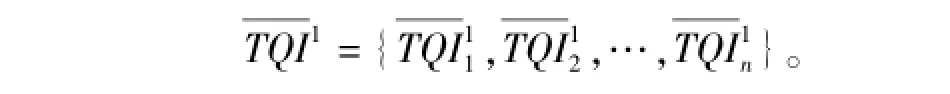
这个结果为对处理后数据的预测，对其按下式进行反向递减计算，可得到对原始TQI序列的预测结果：

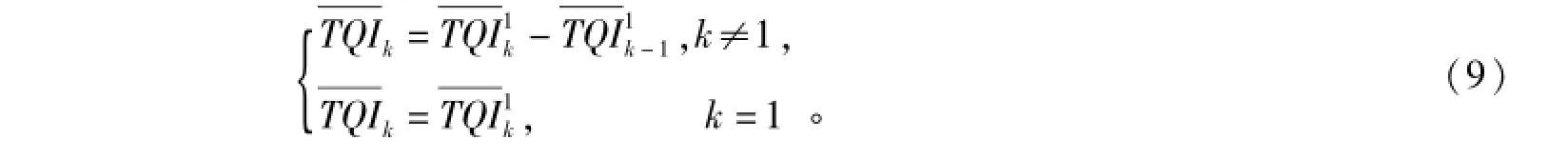
4 算例分析

4.1 数据来源

京九铁路是一条贯穿我国南北的交通大动脉，北起首都北京，南至香港特别行政区，途径9个省市，全长2 536 km。本文所使用的轨检测数据为京九线北段K372．776至K650．333区段的数据，区段长度为227．557 km，采集了2008年2月20日至2010年7月23日共86次检测数据做分析研究。

4.2 TQI与各指标的关联度

TQI值是轨距、水平、左高低、右高低、左轨向、右轨向和三角坑7项指标的标准差之和，这7项指标序列分别用X1，X2，X3，X4，X5，X6，X7表示。对于不同的单元区段，每一个单项指标对TQI的影响程度是不一样的，需要分别考虑。这里，选择上行468.8 km处2009年的10次检测数据作分析。经过反复试验，取ε＝0.5，按照2.1所述方法，对7项指标与整体TQI值进行灰色关联分析，得到计算结果见表1。

表1 TQI值与各指标关联度Table 1 Correlation of TQI value and every index

由表1可以看出，就本单元区段而言TQI值与7项指标之间的关联度大小顺序分别是：三角坑、水平、右轨向、轨距、右高低、左高低、右轨向。并且与三角坑指标之间的关联度远大于其他几项指标。这说明三角坑对整体TQI值得影响是最大的，需要在实际工作中注意预防三角坑超限，使整体区段保持良好状态。

4.3 区间预测

京九线上行K468．2～K469区段2009年1月至2009年10月的TQI检测数据见表2。

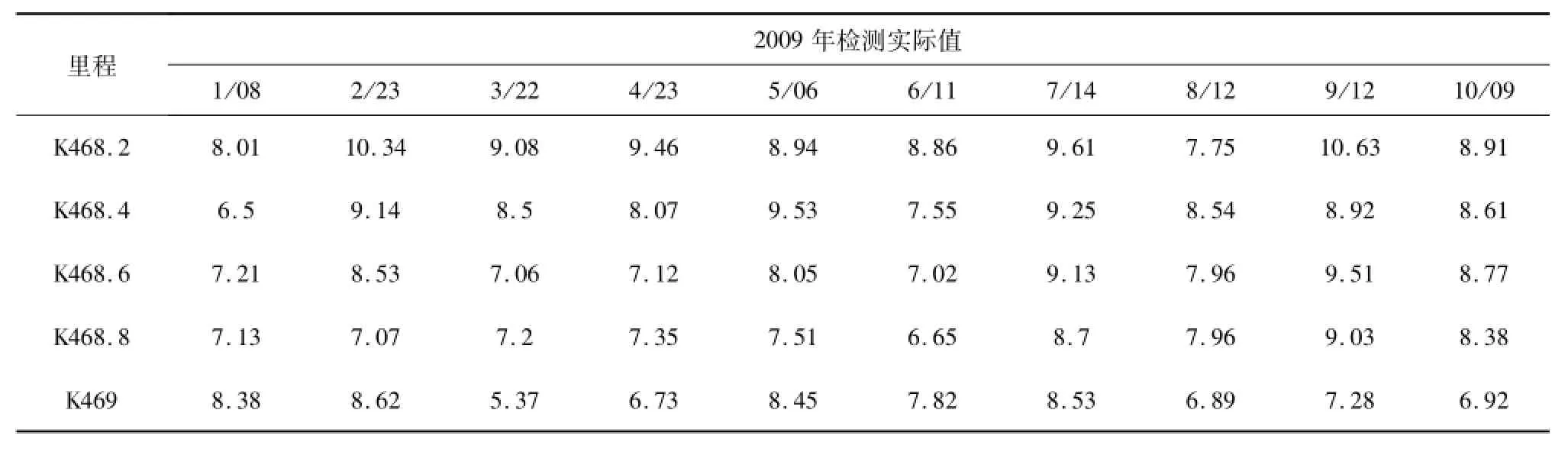
表2 TQI数据表Table 2 TQI data table

以K469处的10次检测数据为例，绘制TQI变化趋势图，见图1。

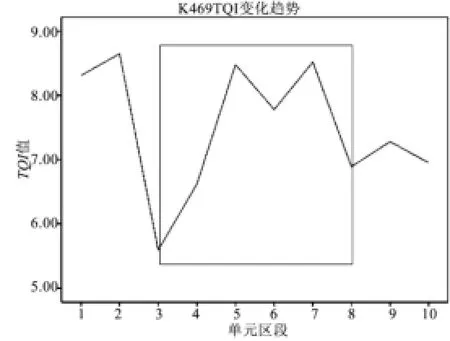
图1 TQI变化趋势图Fig.1 TQIvariety trend

由图1可知，整个变化过程大体分为三个阶段。第一阶段是前三次检测，第三次检测的TQI值较前两次有明显的降低，说明在第二次检测之后发生了维修活动，使轨道质量明显提高。第二阶段是第四至七次检测，在这一期间内TQI总体上成上升的趋势，说明轨道质量在逐步劣化。第三阶段的特点与第一阶段相似。

在整个变化过程中，引起TQI劣化的原因是多方面的，包括自然条件引起的轨道沉降和行车引起的轨道状态的改变等。运用灰色理论，可以避免具体因素的影响，对TQI进行预测和分析。

应用残差修正模型，对5个单元区段2010年11月的TQI检测值进行预测，预测结果见表3。

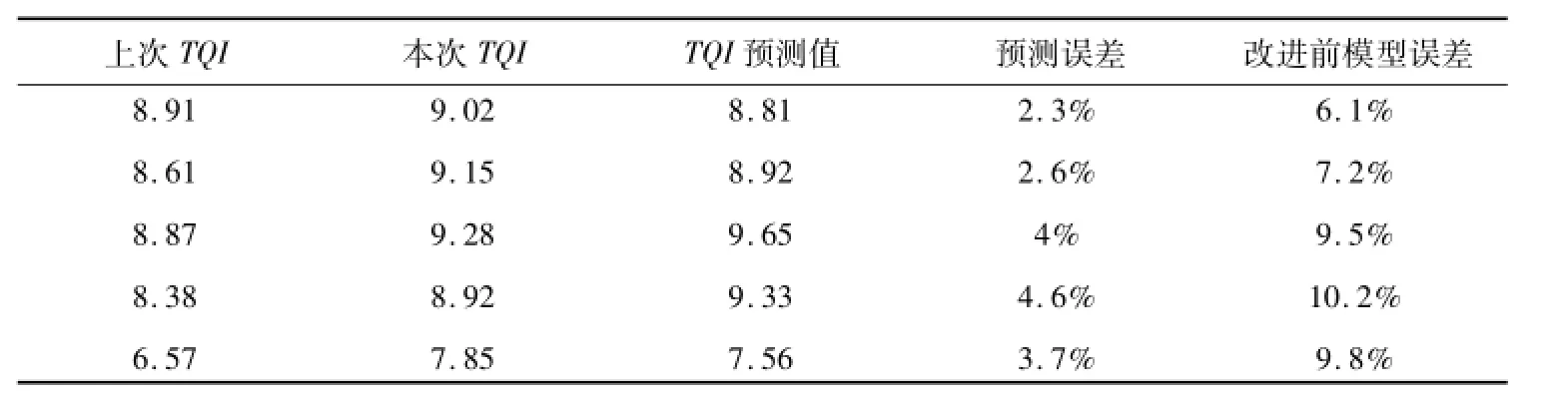
表3 TQI预测结果Table 3 Prediction results of TQI

通过2010年11月的实际检测数据与预测数据对比分析，残差修正模型的预测值可以将预测误差控制在5%以内，较改进前的模型有了很大的提高，对指导实践维修活动更具有实际意义。

4.4 单元区段预测过程

随机选取京九线北段468．6 km的一个200 m单元区段，以2008年3月至2009年3月20次TQI监测数据的实际值作为原始序列，见表4。

表4 TQI检测数据实际值Table 4 The actual value of TQI test data

京九铁路的轨道数据是采用Ⅳ型轨检车检测得到的。Ⅳ型轨检车一般不单独开行，而是编挂在其他列车上。由于受运行速度、传感器灵敏度和其他一些外界条件的影响，会导致一些误差的产生，200 m单元区段TQI的值是通过800个采样点的7项不平顺指标的标准差得到的。但是单个采样点在每次采样中的位置不是绝对固定的，这样即使在不考虑外界环境对检测活动的影响下，每次采样的随机性，也会引入相应的误差，称为选择性偏差。从理论上讲，在没有维修活动发生的情况下，对于同一区段而言，后一次的TQI检测值应该大于等于前一次的检测值，但是考虑到上述误差的影响，实际的检测数据并不完全如此，见图2。

图2 整区段相邻两次TQI检测值Fig.2 The adjacentTQIvalue of the entire segment

为了去除偏离点的影响，将表中后一次检查结果比前一次检查小并且幅度介于0．5到1之间的数据除去，得到修正后的TQI序列，见表5。

表5 TQI检测数据预处理结果Table 5 Preprocessing results of TQI test data

应用公式（8）对表5的数据进行累加，结果见表6。

表6 数据累加结果Table 6 Accumulation results of data

对得到的新序列建立ARMA模型，模型的阶数为p＝2和q＝1，参数为c＝0.023 213，φ1＝0.512 689，φ2＝0.456 254，θ1＝－0．198 625，得到预测结果后，逆推出原始TQI序列的预测值，结果见表7。

表7 进后TQI数据预测结果Tale 7 Improved prediction results of TQI data

如果采用文献［1］中提出的直线预测法，得到的预测值与真实值之间的相对误差平均在12%。表3和表7的预测结果表明，残差修正GM（1，1）和改进的ARMA模型在一定程度上减小了数据本身误差的影响，提高了预测的精度，相对误差｜r｜＜5%，结果比较理想，对指导线路的维修工作，具有一定的借鉴意义。

5 结论与展望

本文首先利用残差修正GM（1，1）模型对不同单元区段的TQI进行预测，得到的结果基本反应了TQI的实际值，同时对影响TQI值得各种指标进行了关联性分析。其次，用改进的ARMA模型针对单元区段建立单独模型进行中长期的预测。两个分析预测模型的结果较精确，对铁路线路的维修工作有一定的实际指导意义。

当有维修活动发生时，TQI值会大幅度降低，导致预测值与实际值的偏差增大，因此如何更好地解决维修活动的影响，是下一步研究的重点。

［1］刘国强，颜颖．国内外高速铁路线路养护维修分析［J］．中国铁路，2006（10）：57－59．

［2］中华人民共和国铁道部．铁路线路修理规则［M］．北京．中国铁道出版社．2007．

［3］徐伟昌．利用轨道质量指数（TQI）预测轨道不平顺发展的探讨［J］．上海铁道科技，2011（2）：5－7．

［4］曲建军，高亮，张新奎，等．基于灰色GM（1，1）非等时距修正模型的轨道质量预测［J］．中国铁道科学，2009，30（3）：5－8．

［5］贾朝龙，徐维祥，王福田，等．基于GM（1，1）与AR模型的轨道不平顺状态预测［J］．北京交通大学学报：自然科学版，2012，36（3）：52－56．

［6］谭冠军．GM（1，1）模型的背景值构造方法和应用［J］．系统工程理论与实践，2000，4（9）；98－103．

［7］李敏，陈胜可．EViews统计分析与应用［M］．北京：电子工业出版社，2011．

［8］李瑞莹，康锐．基于ARMA模型的故障率预测方法研究［J］．系统工程与电子技术，2009，30（8）：1588－1591．

［9］刘思峰，谢乃明．灰色系统理论及其应用［M］．北京．科学出版社．2008．

［10］王建玲，刘思峰，邱广华，等．基于信息集结的新型灰色关联度构建及应用［J］．系统工程与电子技术，2010，32（1）：77－81．

Time sequence model based track quality index prediction

SONG Bo-yang
（School of Traffic and Transportation，Beijing Jiaotong University，Beijing 100044，China）

Track quality index（TQI），a time series with random characteristics，is an important indicator reflecting the total unevenness of a track segment．We analyze the correlation betweenTQIsequence and every single indicator with grey theory and predict next inspection value of a certain segment．Moreover，we investigateTQIsequence data for 200 m track segment with auto-regressive moving average（ARMA）model，analyze their variation tendency and predictTQIvalue in future time．Analysis show that the accuracy of each model has been improved，and the relative error is less than 5%．

time sequence；ARMA model；correlation；fitted GM（1，1）；TQI

U216

A

1002-4026（2014）03-0066-07

10.3976／j.issn.1002－4026.2014.03.013

2014-02-15

宋博洋（1990－），男，硕士，研究方向为交通运输工程，运输系统工程。Email：13125720＠bjtu．edu．cn