电磁层析成像系统中标量磁势的数值解法

赵 倩，郝建娜，尹武良

(天津大学电气与自动化工程学院，天津 300072)

电磁层析成像系统中标量磁势的数值解法

赵 倩，郝建娜，尹武良

(天津大学电气与自动化工程学院，天津 300072)

电磁层析成像技术是一种基于电磁感应定律的工业过程成像技术，激励线圈产生的交变磁场在目标物体中产生涡流，进而产生二次磁场．接收线圈检测到感应电压后利用重建算法可以得到物场的分布信息．边界元法以积分方程为数学基础，同时采用了与有限元法相似的划分单元离散技术，将边界积分方程离散为代数方程组后用数值方法求解．边界元法在电磁层析成像技术中已有一定的应用，而基于标量磁势的边界元法使得求解过程的速度和效率显著提高．本文针对一个简化的电磁层析成像系统模型，利用3种数值方法求解目标物体表面的标量磁势，并利用Matlab编程得到仿真结果．对结果进行对比分析后，选出最优解法．

电磁层析成像；边界元法；标量磁势；数值仿真

电磁层析成像(electromagnetic tomography，EMT)技术是20世纪90年代发展起来的一种新型电学层析成像(electrical tomography，ET)技术，EMT技术基于电磁感应原理，载流线圈在目标物体中产生涡流，进而激励出二次磁场，这样接收线圈可以测量到感应电压．最后采用一定的图像重建算法得到被测场域内的分布信息．它具有非接触、非侵入、响应快速、信息量丰富等特点，因而在工业生产过程和生物医学领域都有着广泛的应用前景[1-7]．

边界元法(boundary element method，BEM)具有边界积分方程的深厚的数学根基．它以边界积分方程为数学基础，通过单元离散技术将边界离散为边界元，将边界积分方程离散为代数方程组．再用数值方法求解代数方程组，从而得到原问题边界积分方程的解．边界元法的优点为可以降低求解问题的维数，提高了求解效率，并且由于求解过程中采用了解析基本解，所以具有更高的精度[8-14]．

BEM在EMT中的应用已经有了许多的研究[15].在边界元法求解电磁问题的过程中，标量磁势作为基本变量具有重要意义．在求解外部磁场分布之前，需要先求出目标物体表面的标量磁势，以此为基础再进行后续计算．目前对于标量磁势的求解方法一般表示为对要求点处求立体角[16]，该方法同样涉及如何求解积分的问题．对于复杂不规则物体，快速多极算法是一种快速有效的计算方法[17]．但是该算法的步骤较为繁琐，对于一些简单问题反倒不适用．

笔者通过建立一个简单的EMT系统模型，推导出标量磁势的最终表达式．通过3种不同的数值方法——曲面积分定义法、高斯-勒让德积分公式法和积分坐标变换法，分别仿真得到不同的结果．对这些数据进行分析可以得出，在保证其他条件不变和相同求解精度的前提下，高斯-勒让德积分公式法是最简单快速的方法．

1 建立模型并推导公式

假设一个简单的EMT系统，只含有1个激励线圈和1个接收线圈．激励线圈和接收线圈的中心分别位于(0，0，4,m)和(0，0，-4,m)处，半径均为1,m．目标球体为一般金属，中心位于原点，半径为1,m．

对于恒定磁场，由磁场环路定理可得

式中L为曲面S的边界．这种情况下如果想引入标量磁势，其前提条件是，对于求解区域内的任何闭合回路，都有

根据上面推导出的公式，这里采用了3种方法来求解球体表面离散点处的标量磁势．之后利用Matlab仿真，对这3种方法的求解速度和所得数据精度进行了分析对比．

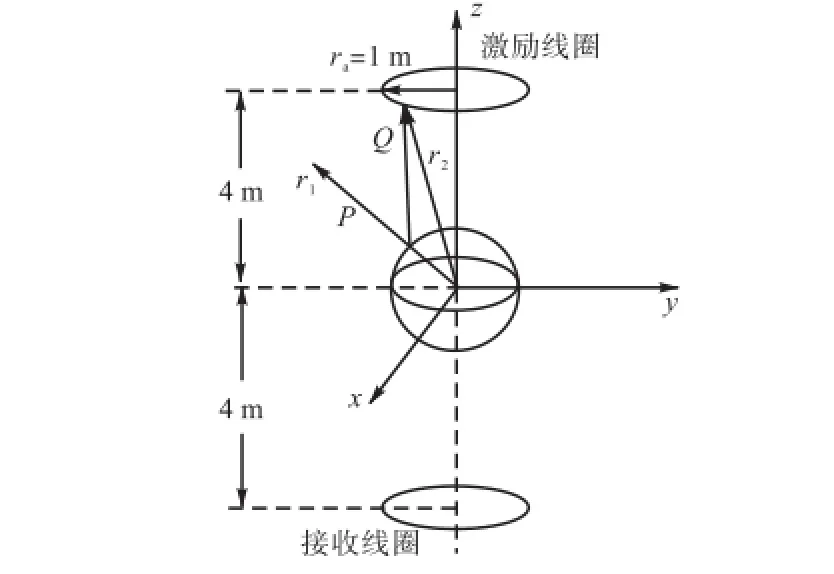
图1 一个简单的EMT系统Fig.1 A simple EMT system

在实际应用中，对于单连通，不存在自由电流的区域，全区域皆可以引入标量磁势描述磁场．如果区域中存在自由电流，则挖去电流及电流线围着的一个曲面S，剩余空间里磁场是无旋的[18-19]，可以假设为标量磁势，A．

图1所示的EMT系统中，载流线圈在物体表面产生的磁场可由毕奥-萨伐儿定理求出[19]，即

式中：上标pr表示外部激励产生的场量；B为磁感应强度；r=r1-r2，r1为球面上的点到原点的矢径，r2为激励线圈所围平面上的点到原点的矢径．

式中：S为由激励线圈L围成的平面；n0为S的单位法向量．

对场域中的球体表面进行三角形网格划分，如图2所示，可以得到38个离散点和72个网格．划分时，纵轴z的范围为1,m到-1,m，每隔0.2,m取一组，对应11个不同的z值．在每个z确定的圆上，角度范围为0到2π，间隔为π/2．

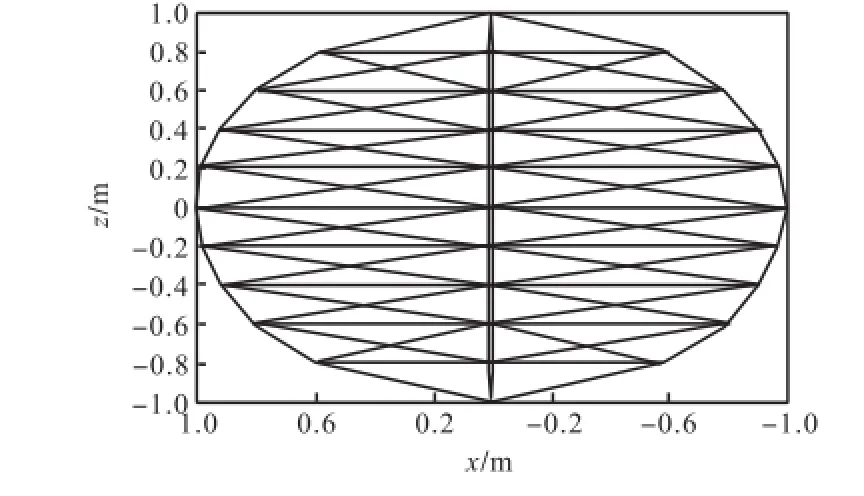
图2 EMT系统中球体表面的网格划分Fig.2 Mesh of the target surface in the EMT system

若激励线圈上载有单位电流，即I=| I |=1,A，则球体表面由外加磁场产生的标量磁势为

2 Matlab数值仿真

2.1 由曲面积分的定义求解(方法1)

由曲面积分的定义可得[20]，通过将积分区域划分成正方形网格，可将积分离散化，有

式中：iSΔ为第i个正方形网格的面积；2ir为激励线圈所围平面上的点到原点的矢径．在式(6)中，积分平面为激励线圈所包围的圆面，将该平面分成N个小正方形，r2i为矢径取第i个正方形的中心到原点的矢径．首先对r2i的位置进行判断，若是在圆内则将其带入积分公式；若在圆外，则其对积分的作用为0；再将所有的积分进行求和，最终得到在球体表面每个离散点处的标量磁势．

由仿真结果可得，随着划分网格数目的增多，积分结果成收敛趋势．当网格数为6,400时，积分基本不再变，计算时间为t=0.556,122,s．38个离散点对应11个z值，通过仿真可知，每个z值相同的点具有相等的标量磁势，故可用11个不同z值上的标量磁势来表示所有离散点处的标量磁势．

表1 方法1得到的标量磁势Tab.1 Magnetic scalar potential obtained by the first method

以表1第1行为例，可以画出随着网格数增加标量磁势逐渐收敛的仿真图形，如图3所示．

由于每个确定的z值对应的圆上的4个点处具有相同的标量磁势，所以下面的表格中可以只列出不同z值处的标量磁势．图4为x=0处的球体切面上的等势线，可以看出，球体从上往下标量磁势逐渐减小，并且在每个确定z值处具有相同的标量磁势．

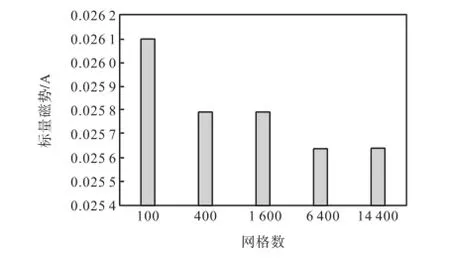
图3 随着网格数标量磁势数值逐渐收敛Fig.3Convergence of the magnetic scalar potential as the increase of mesh

图4 x=0处的切面上等势线分布Fig.4 Isopotential lines on the section where x=0

2.2 利用N段高斯-勒让德积分公式来求解(方法2)

首先将面积分转换成二重积分[21]为

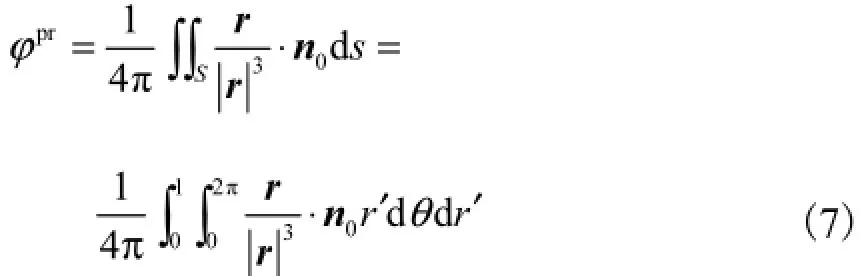
则原积分可以简写为

积分变量θ和r′分别表示角度和半径，积分函数为

对积分区间进行标准化得

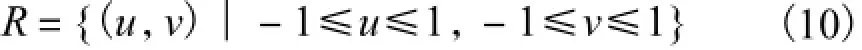
变换方程为

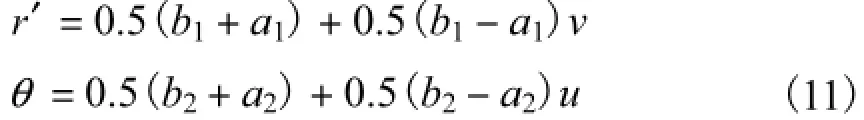
则

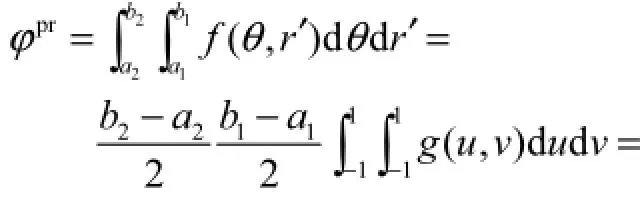
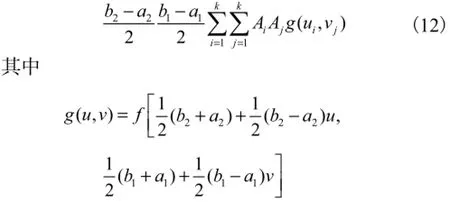
式中：n为节点数；k为插值节点数；Ai和Aj(i，j=1，2，…，R)均为系数矩阵A中第i个和第j个值．具体的节点和对应的系数矩阵如表2所示．为了使精度更高，在这里先将积分区域划分为N段小区域，然后在每段小区域上进行插值积分运算．运行程序得到的结果表明，当N=2，即分成2段，然后进行5点插值可得高精度的解，用时为t=0.109,799,s．

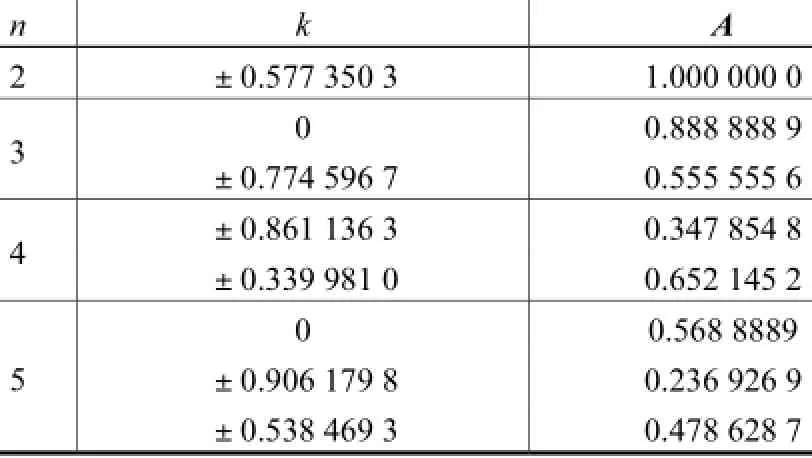
表2 高斯-勒让德积分公式的节点及系数矩阵Tab.2 Nodes and coefficient matrices of Gaussian-Legendre integral formula

由表3可知，对于N(N=1，2，4)段积分公式而言，所求得的标量磁势基本与N无关．只有在z=0时，不同N对应的求解结果才有细微差别．故可知，利用N段高斯-勒让德积分公式来求解标量磁势时，段数N对结果精度的影响甚微，从而为了节约计算时间，可以直接使用1段5点积分公式来求解．

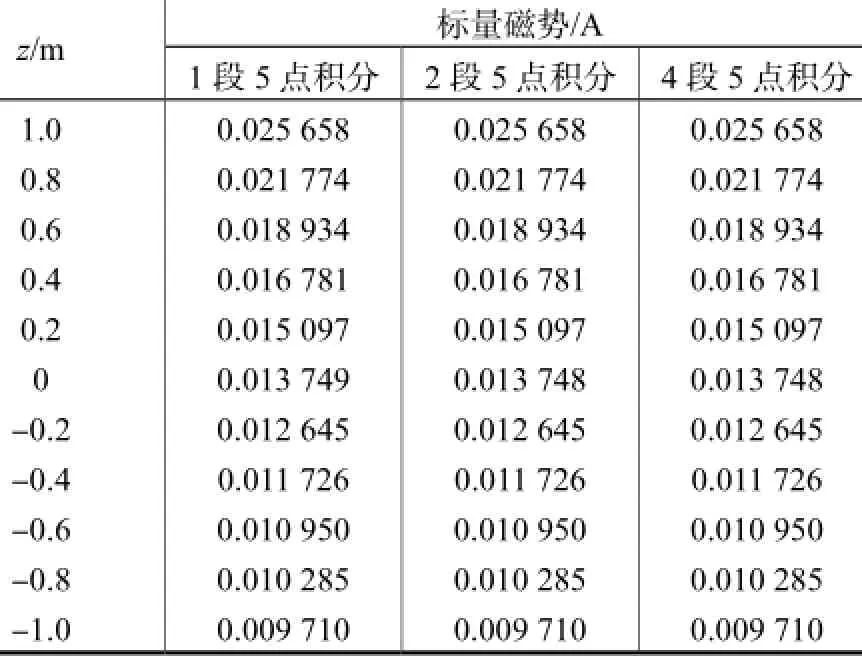
表3 方法2得到的标量磁势Tab.3 Magnetic scalar potential obtained by the second method

2.3 利用积分坐标变换法来求解(方法3)

这种方法首先将积分平面划分为三角形网格，然后利用坐标系转换得到的积分公式来求解[22-24]．

划分网格时，先将圆面上的点进行离散，然后按照逆时针顺序将点依次连接为三角形．根据其中心点的位置，可以判断出三角形是否在圆内．为了方便求解，在这里将全局坐标系转换为局部坐标系．对每个网格而言，新坐标系平行于该网格所在的平面，并且以其中的一边为其横坐标．坐标系的各参数项如图5所示．

图5 局部坐标系与全局坐标系的关系及局部坐标系中的参数Fig.5 Relationship between the local coordinate system and the global coordinate system and the parameters of the local coordinate system

采用与文献[22]中类似的参数和函数，这里以一个三角形网格为例．

V1、V2和V3为第e个三角形网格eΓ的3个顶点．iS∂为eΓ的第i条边．li、si和mi(i=1，2，3)分别是iS∂的长度、单位切向量和单位法向量．则局部坐标系可以定义为

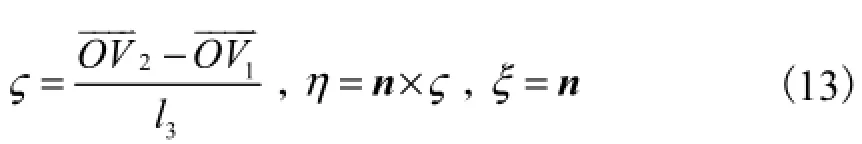
根据以上所列参数，则原积分可化为

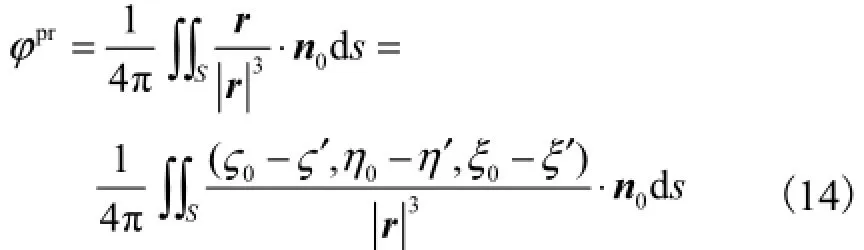
其中n0=(0,0,1)，ξ′=0．故有

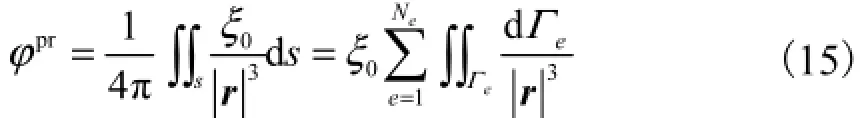
式中Ne为三角形网格的个数．

由文献[22]可得eΓ上的积分为

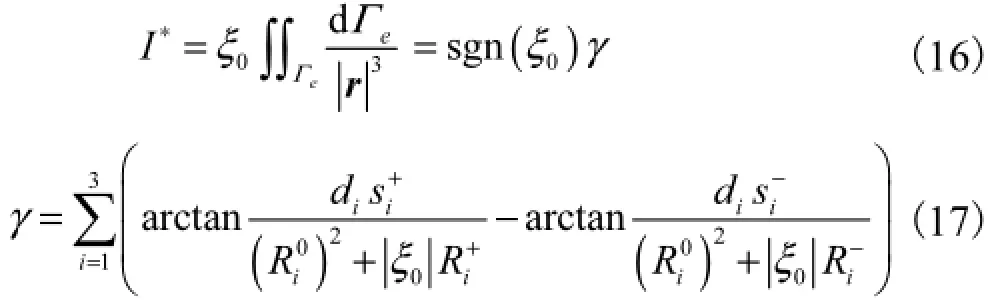
数值计算表明，当网格数为12,800时，标量磁势可以收敛，但用时较长，t=157.126,357,s．

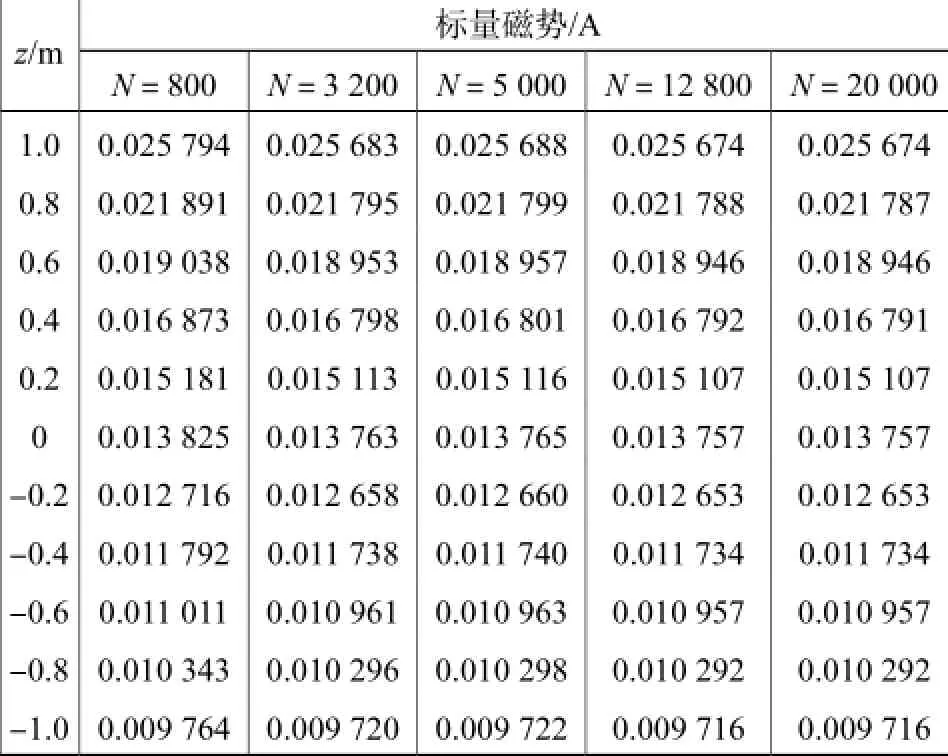
表4 方法3得到的标量磁势Tab.4 Magnetic scalar potential obtained by the third method

2.4 利用Matlab进行数据对比分析

利用Matlab软件对3种方法得到的数据进行分析，如图6所示．

从图6可以看出，3种方法得到的数值解具有很好的一致性，即3种方法都可以得到精确的解，从程序运行时间上看，高斯-勒让德积分公式用时最短，t=0.109,799,s，积分坐标变换法用时最长，t= 157.126,357,s．

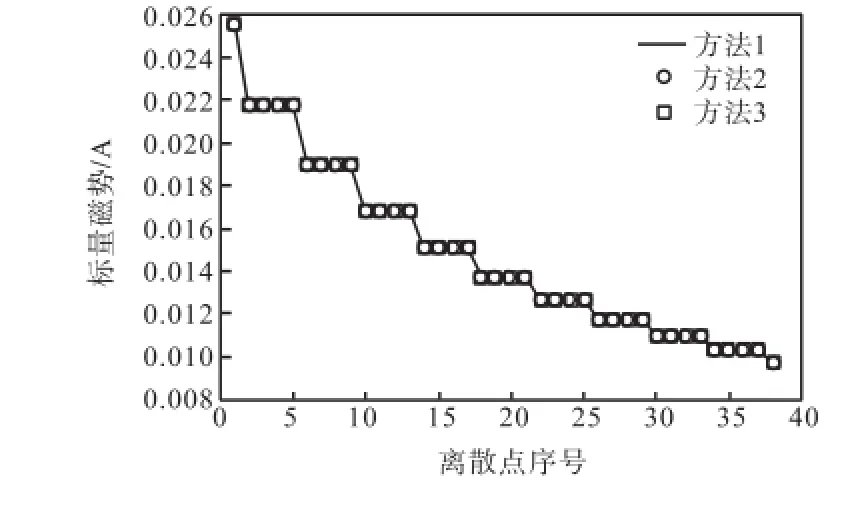
图6 3种方法得到的数据曲线Fig.6 Results obtained by the three methods

3 结 语

快速求解标量磁势为后续计算磁场分布提供了良好基础．本文采用了3种数值方法来求解物体表面的标量磁势，通过以上计算可以看出，以上3种方法都能有效求解目标物体表面的标量磁势．若综合考虑的话，高斯-勒让德积分公式是最好的计算方法，不仅精度高，而且速度快．

［1］ Griffiths H. Magnetic induction tomography[J]. Meas Sci Technol，2001，12：1126-1131.

［2］ Watson S，Wee H C，Griffiths H，et al. A highly phase-stable differential detector amplifier for magnetic induction tomography[J]. Physiol Meas，2011，32：917-926.

［3］ Watson S，Williams R J，Gough W A，et al. A magnetic induction tomography system for samples with conductivities less than 10 S·m-1[J]. Meas Sci Technol，2008，19：1-11.

［4］ Yin W L，Peyton A J. A planar EMT system for the detection of faults on thin metallic plates[J]. Meas Sci Technol，2006，17：2130-2135.

［5］ Soleimani M，Lionheart W R B，Riedel C H，et al. Forward problem in 3,D magnetic induction tomography(MIT)[C]//Proc 3rd World Congr Industrial Process Tomography. Banff，Canada，2003：275-280.

［6］ Yin W L，Peyton A J. Sensitivity formulation including velocity effects for electromagnetic induction systems[J]. IEEE Transactions on Magnetics，2010，46(5)：1172-1176.

［7］ Yin W L，Peyton A J，Zysko G，et al. Simultaneous noncontact measurement of water-level and conductivity [J]. IEEE Transactions on Instrumentation and Measurement，2008，57：2665-2669.

［8］ Brebbia C A，Telles J C F，Wrobel L C. Boundary Element Techniques：Theory and Applications in Engineering[M]. New York：Springer -Verlag，1984.

［9］ 姚振汉，王海涛. 边界元法[M]. 北京：高等教育出版社，2010.

Yao Zhenhan，Wang Haitao. The Boundary Element Method[M]. Beijing：Higher Education Press，2010(in Chinese).

［10］ 刘永健，姚振汉. 三维接触边界元法的一种误差直接估计[J]. 清华大学学报：自然科学版，2003，43(11)：1499-1502.

Liu Yongjian，Yao Zhenhan. Direct error estimate for the boundary element method for a 3-D contact problem[J]. Journal of Tsinghua Univ：Sci & Tech，2003，43(11)：1499-1502(in Chinese).

［11］ 单 磊，董天临. 应用边界元法对电磁场计算的分析及优化[J]. 信息通信，2007，33(1)：31-33.

Shan Lei，Dong Tianlin. Analysis and optimization of boundary element method to irregular electromagnetic field[J]. Information & Communications，2007，33(1)：31-33(in Chinese).

［12］ Harrington R F. Field Computation by Moment Methods[M]. New York：Acmillan Company，1968.

［13］ Banerjee P K. The Boundary Element Methods in Engineering[M]. New York：McGraw-Hill Book Company，1994.

［14］ Chen W，Fu Z. A novel numerical method for infinite domain potential problems[J]. Chinese Science Bulletin，2010，55(16)：1598-1603.

［15］ Pham M H，Peyton A J. A model for the forward problem in magnetic induction tomography using boundary integral equations[J]. IEEE Transactions on Magnetics，2008，44(10)：2262 -2267.

［16］ 张泽明，邓亦仁. 运用毕-沙定律导出磁标量位表达式的新方法[J]. 重庆建筑工程学院学报，1985(4)：99-103.

Zhang Zeming，Deng Yiren. A new method using Biot-Savart Law to derive magnetic scalar potential notation[J]. Journal of Chongqing Institute of Civil Engineering and Architecture，1985(4)：99-103(in Chinese).

［17］ Hafla W，Buchau A，Rucker W M. Efficient computation of source magnetic scalar potential [J]. Adv Radio Sci，2006，4：59-63.

［18］ 阮放鸣. 有限区域里的磁标势和磁多极展开[J]. 贵州师范大学学报：自然科学版，1997，15(3)：102-107.

Ruan Fangming. Magnetic scalar potentials in finite regious and the multipole expansion in material media[J]. Journal of Guizhou Normal University：Natural Science，1997，15(3)：102-107(in Chinese).

［19］ 谢处方，饶克谨. 电磁场与电磁波[M]. 北京：高等教育出版社，1987.

Xie Chufang，Rao Kejin. The Electromagnetic Field and Waves[M]. Beijing：Higher Education Press，1987(in Chinese).

［20］ 同济大学数学教研室. 高等数学 [M]. 4版. 北京：高等教育出版社，1996.

The Mathematical Teaching Team of Tongji University. Advanced Mathematics[M]. 4th ed. Beijing：Higher Education Press，1996(in Chinese).

［21］ 张 军. 数值计算[M]. 北京：清华大学出版社，2008.

Zhang Jun. Numerical Computation[M]. Beijing：Tsinghua University Press，2008(in Chinese).

［22］ Graglia R D. On the numerical integration of the linear shape functions times the 3-D Green's function or its gradient on a plane triangle [J]. IEEE Transactions on Antennas and Propagation，1993，41(10)：1448-1455.

［23］ Morrison J A. Integral equations for electromagnetic scattering by perfect conductors with two-dimensional geometry [J]. Bell Syst Tech J，1979，58(2)：409-425.

［24］ Graglia R D. Static and dynamic potential integrals for linearly varying source distributions in two- and threedimensional problems [J]. IEEE Transactions on Antennas and Propagation，1987，AP-35(6)：662-669.

(责任编辑：孙立华)

Numerical Approach for the Magnetic Scalar Potential of Electromagnetic Tomography System

Zhao Qian，Hao Jianna，Yin Wuliang
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

Electromagnetic tomography (EMT) is an industrial process tomography based on the Faraday law of electromagnetic induction. In EMT, current-carrying coils are used to induce eddy currents in the object which in turn radiates a scattered field. The induced voltages are sensed with receiving coils and image reconstruction algorithms are used to solve for the spatial distribution of the complex conductivity in the target. Boundary element method (BEM) based on integral formulations is an effective way to analyze the problems of EMT system. By adopting the similar mesh technique as FEM, the boundary integral equations can be transformed into linear equations. Then numerical method is used to solve the linear equations and the solution of the original integral equations can be obtained. The magnetic scalar potential was the important part of the application of BEM into EMT which improves efficiency and speed. Three numerical approaches were used to calculate the magnetic scalar potential on the surface of the target for a simple EMT model. With the aid of Matlab, the optimal method was chosen by comparing the results obtained by the three methods.

electromagnetic tomography；boundary element method；magnetic scalar potential；numerical simulation

O241.8

A

0493-2137(2014)07-0613-06

10.11784/tdxbz201210003

2012-10-06；

2013-01-23.

国家自然科学基金国际重大合作资助项目(60910001)；教育部博士点基金资助项目(20090032110062).

赵 倩（1987— ），女，博士研究生，shmilyshenzhen@163.com.

尹武良，wuliang.yin@gmail.com.