单轴旋转式激光陀螺捷联惯导系统对准精度分析

刘永红, 刘明雍, 谢 波

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 中国航天科技集团公司 第九研究院十六研究所, 陕西西安, 710100)

单轴旋转式激光陀螺捷联惯导系统对准精度分析

刘永红1, 刘明雍1, 谢 波2

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 中国航天科技集团公司 第九研究院十六研究所, 陕西西安, 710100)

设计了单轴旋转式激光陀螺捷联惯导系统的对准方案, 分析了影响旋转对准精度的惯性器件误差参数,同时对不同惯性器件误差对应的对准精度进行了比对分析, 并进行了仿真试验验证。仿真结果表明, 天向陀螺标度因数非对称性误差、天向陀螺标度因数误差对航向角对准精度的影响较大, 该结论可为单轴旋转式激光陀螺捷联惯导系统的设计提供参考。

捷联惯导系统; 对准精度; 惯性器件; 标度因数

0 引言

捷联惯导系统初始对准就是确定从载体坐标系到计算地理坐标系的初始姿态矩阵, 并且进行姿态校准[1]。在静基座条件下, 捷联惯导系统的可观测性较差, 而在采用卡尔曼滤波进行捷联惯导系统精对准过程中, 系统的观测性直接影响滤波器进行状态估计的收敛速度和估计精度。在单轴旋转的捷联惯导系统中, 通过惯性测量单元(inertial measurement unit, IMU)的转动可改变系统误差模型中的姿态矩阵, 从而改善定位定向系统的可观测性[1]。因此, 单轴旋转对准是一种提高对准精度快速对准时间的有效方法。单轴旋转式激光陀螺捷联惯导系统的旋动并没有提高惯性器件本身的精度, 惯性器件的误差依然存在, 只是消除或减小了惯性器件的常值漂移对对准计算结果的影响。但同时惯性器件各误差项在单轴旋转下也会发生变化, 给对准精度带来一定影响。本文先对单轴旋转式激光陀螺捷联惯导系统的对准方案进行了设计, 然后对影响旋转对准精度的主要惯性器件误差参数做了分析, 并通过仿真试验对所设计的对准方案进行验证, 同时对比分析了不同惯性器件误差对应的对准精度, 可为单轴旋转式激光捷联惯导系统的设计提供参考。

1 对准方案设计

1.1 转动方案设计

单轴旋转可以补偿惯性元件在与旋转轴垂直的平面上的惯性仪表常值漂移。为了减小旋转过程中惯性器件误差效应的影响, 一般采取正转反转相结合的方式进行旋转[2], 本文设计的对准阶段的转动方式见图1。

首先, 在A点停止T0;

次序1: 从A点出发逆时针转180°, 到达位置B点, 停止时间Ts;

次序2: 从B点出发逆时针转180°, 到达位置A点, 停止时间Ts;

次序3: 从A点出发顺时针转180°, 到达位置B点, 停止时间Ts;

次序4: 从B点出发顺时针转180°, 到达位置A点, 停止时间Ts;

然后按照次序 1～4的顺序循环运动; 最后,在A点停止T0。

图1 单轴转动方案设计图Fig. 1 Rotation scheme of single axis

1.2 对准算法设计

1.2.1 粗对准算法设计

假设导航坐标系为东北天地理坐标系, 载体惯性坐标系(ib0系)在粗对准开始时刻t0将b系在惯性空间中凝固成为ib0系[3], 即(t0)=I。初始对准姿态矩阵可表述如下

式中, 设对准位置的纬度为L, 经度为λ, e 系相对于i 系转过的角度ωiet, 则

1.2.2 精对准算法设计

当不存在线运动时单轴旋转捷联惯导系统的姿态误差方程和速度误差方程为

在单轴旋转捷联惯导系统精对准过程中, 利用卡尔曼滤波器完成姿态误差角的最优估计。由于陀螺零位误差和加速度计零偏误差并不完全是白噪声, 为了使单轴旋转捷联惯导系统的误差方程适合卡尔曼滤波模型, 将陀螺零位误差和加速度计零偏误差扩充为状态变量[1]。故, 通常选取状态变量

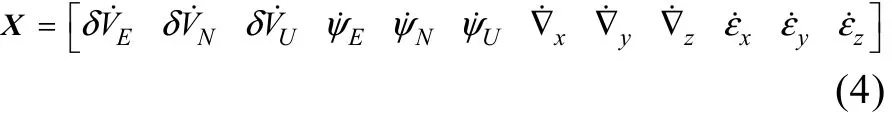
则系统状态方程为

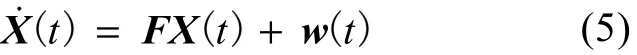
其中

其中:ωU= ωiesin L , ωN= ωiecos L 为地球自转在天向和北向上的分量;Cij为姿态矩阵的矩阵元。

在单轴旋转捷联惯导系统中, 很难保证 3个加速度计的安装位置不偏离系统的质心, 在外界和自身角运动的情况下, 3个加速度计会敏感到附加的切向加速度和向心加速度。若把这些附加的加速度当作来自于理想“点测量组件”的输出进行导航解算, 将从原理上引起导航误差, 即尺寸效应误差[4]。因此选取速度误差作为观测量时,应先对速度进行尺寸效应误差补偿, 具体补偿算法文献[4]中有详细推导, 本文对此不展开介绍。

选取经过尺寸效应误差补偿的速度误差作为观测量, 则建立系统的观测方程为

2 对准误差源分析

传统单位捷联惯导系统初始对准水平姿态对准精度与水平加速度等效零偏有关, 方位对准精度与等效零位有关。单轴旋转式捷联惯导系统由于增加了单轴旋转过程, 因此, 对准误差源也会发生相应变化。在单轴旋转式捷联惯导系统中由于影响对准精度的因素较多, 本文假设旋转轴误差、测角器件误差、换向超调误差、转速控制误差等可以忽略, 仅考虑惯性器件误差对对准精度的影响。由于惯性器件的标度因数和安装误差无法标定的绝对准确, 而且标度因数和安装误差还可能随着时间、环境等因素发生改变, 实际系统中总存在着惯性元器件的标度因数误差和安装误差。另外, 由于原理和工艺等原因, 一般标度因数还存在着正反不对称性, 实际的使用过程中往往忽略了这种不对称性, 或者把标度因数直接取为正向标度因数和反向标度因数的平均值, 这也会引起一定的标度因数不对称误差[2,5]。

下面对单轴旋转式捷联惯导系统中影响对准精度的陀螺和加速度计误差进行分析。为了分析方便, 假设1.1节中Ts=0, T0=0, 也就是对准期间是一个连续正反旋转的过程。同时假设导航坐标系为东北天地理坐标系, 且初始时刻姿态矩阵为单位矩阵, 初始时刻的东北天方位和 3个陀螺的敏感轴重合, 且使旋转系统的转轴和IMU本体坐标系的坐标轴近似重合, 从0时刻开始, 控制系统的IMU绕竖直方向以角速度ω开始匀速转动。

2.1 陀螺误差

由式(9)可以看出, 在单轴旋转式捷联惯导系统中影响对准精度的主要陀螺误差为安装误差Exy, Eyx, 标度因数误差E1z, 陀螺的标度因数非对称性误差E1zf和陀螺零位误差E0x,E0y,E0z。其中,E1zf对航向角对准精度的影响约为 Δϕf=（/2）·旋转圈数, 如= 10−4,且整个对准过程中共旋转12圈, 则Δϕf=0.216 0°

2.2 加速度计误差

IMU机体系中由加速度计的零偏、标度因数误差和安装误差所产生的速度误差为

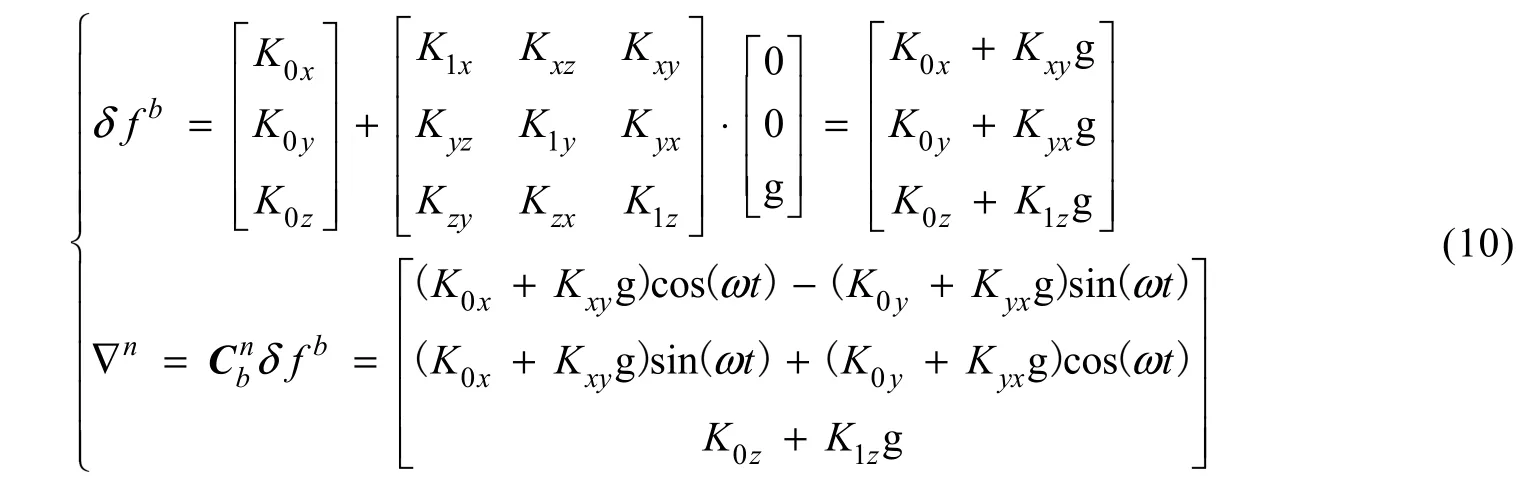
由式(10)可看出, 在单轴旋转式捷联惯导系统中影响对准精度的主要加速度计误差为安装误差K, K, 标度因数误差 K1z, 加速度计安装误差K,K和 K。

3 仿真结果与分析

对1.1节旋转方式进行仿真, 在位置A静止18.5 s, 然后以18°/s逆时针旋转180°到达位置B,在位置B停止1 s, 再以18°/s逆时针旋转180°到达位置A, 在位置A停止1 s, 再以18°/s顺时针旋转180°到达位置B, 在位置B停止1 s, 再以18°/s顺时针旋转180°到达位置A, 在位置A停止1 s;共循环6次, 最后在位置A静止18.5 s。整个流程共300 s。设置陀螺和加速度计的误差参数如下。

陀螺零偏常值误差为0.01°/h, 水平陀螺标度因数误差、天向陀螺标度因数误差、水平陀螺标度因数不对称、天向陀螺标度因数不对称性均为10-5,陀螺安装误差为10-5rad。

加速度计零偏常值误差为100 µg, 标度因数误差为10-4、安装误差为10-5rad。

15 s粗对准后, 再进行精对准。旋转调制对准过程中姿态角特别是航向角是不断变化的。图2～图4为旋转调制对准的姿态估计曲线图。可以看出, 300 s俯仰角对准误差为0.000 7°, 横滚角对准误差为–0.001 0°, 航向角对准误差为0.025 2°。

第2节中, 虽然对影响对准精度的主要误差参数进行了分析, 但无法进行具体量化。为了进一步分析惯性器件误差对对准精度的影响, 其他误差参数保持不变, 对主要影响对准精度的不同惯性器件误差和对应的对准精度通过仿真试验进行了比对分析, 结果见表1。从表中可知: 1) 这些误差参数中对航向角对准精度影响较大的是天向陀螺标度因数非对称性误差, 这与2.1节的分析结果相吻合。E1zf为10-5, 5×10-5和10-4分别对应的航向角对准误差为 0.025 2°, 0.108 2°和0.212 0°。2) 天向陀螺标度因数误差E1z对航向角的对准精度影响较明显, E1z为10-5, 5×10-5和10-4分别对应的航向角对准误差为0.025 2°, 0.032 4°和0.041 4°。3) 陀螺安装误差Exy和Eyx对水平姿态对准影响较明显, 但对航向角对准精度影响较小。4) 相对而言, 加速度计误差对对准精度影响较小。

图2 俯仰角估计曲线图Fig. 2 Estimation curve of pitch angle

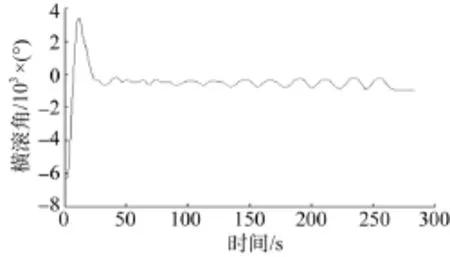
图3 横滚角估计曲线图Fig. 3 Estimation curve of roll angle

图4 航向角估计曲线图Fig. 4 Estimation curve of course angle

4 结束语

本文对单轴旋转式激光陀螺捷联惯导系统的对准方案进行了设计, 对影响对准精度的主要惯性器件误差进行了分析。通过仿真试验对所设计的对准方案进行了验证, 并比对分析了不同惯性器件误差对应的对准精度。从比对结果可看出,对航向角对准精度影响较大的是天向陀螺标度因数非对称性误差和天向陀螺 E1z, 而陀螺安装误差Exy和Eyx对水平姿态对准影响较明显, 但对航向角对准精度的影响较小, 此外和陀螺相比较, 加速度计误差对对准精度影响较小。

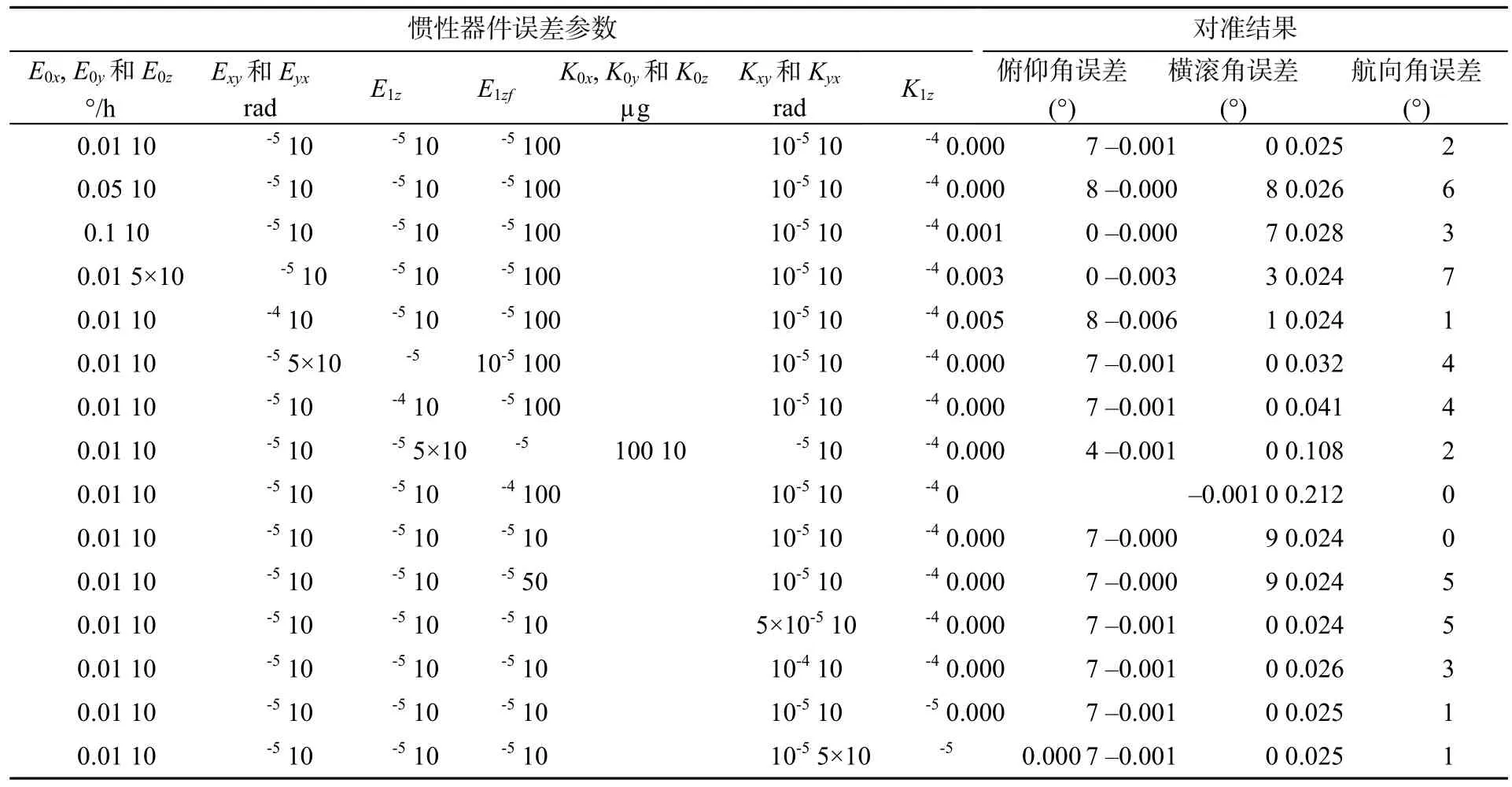
表1 对准结果比对分析表Table 1 Comparison of alignment results

参考文献:

[1] 孙枫, 孙伟. 旋转捷联惯导系统精对准技术[J]. 系统工程与电子技术, 2010, 3(3): 630-633.

Sun Feng, Sun W ei. Fine Alignment by Rotation in Strapdown Inertial Navigation Systems[J]. Systems Engineering Electronics, 2010, 3(3): 630-633.

[2] 袁保伦. 四频激光陀螺旋转惯导系统研究[D]. 长沙:国防科技大学, 2007.

[3] 周章华. 一种单轴旋转捷联惯导系统抗晃动快速自对准方法[J]. 中国惯性技术学, 2011,19(6): 648-653.

Zhou Zhang-hua. Fast Self-alignment Method for Single axial Rotation SINS on Disturbing Base[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 648-653.

[4] 严恭敏, 严卫生, 徐德民. 捷联惯性测量组件中内杆臂效应分析与补偿[J]. 中国惯性技术学报, 2008, 16(2): 148- 153.

Yan Gong-min, Yan Wei-sheng, Xu De-min. Analysis and Compensation on Inner Lever Arm Effect of Strapdown Inertial Measurement Unit[J]. Journal of Chinese Inertial Technology, 2008, 16(2): 148-153.

[5] 祝燕华, 蔡体菁. 旋转式光纤捷联惯导系统的误差效应分析[J]. 中国惯性技术学报, 2011, 19(1): 140-144.

Zhu Yan-hua, Cai Ti-jing. Error Analysis of Rotating Strapdown Inertial Navigation System Based on FOG[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 140-144.

[6] Ishibashi S, Tsukioka S, Sawa T. The Rotation Control System to Improve the Accuracy of an Inertial Navigation System Installed in an Au tonomous Underwater Vehicle[C]//Workshop on Scientific Use of Submarine Cables and Related Technologies, 2007: 495-498.

[7] Ishibashi S, Tsukioka S, Yoshida H. Accuracy Improvement of an Inertial Navigation System Brought about by the Rotational Motion[C]//Oceans 2007. Europe, 2007: 1-5.

[8] Ma Tao, Gao Yan-bin. Application and Comparison of Two Methods for Alignment of Fog SINS[C]//Jinan: 2010 8thWorld Congress on Intelligent Control and Automation, 2010: 3581-3584.

[9] Ahn H S, Won C H. Fast Alignment Using Rotation Vector and Adaptive Kalman Filter[J ]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 70-83.

(责任编辑: 杨力军)

Analysis of Alignment Accuracy for Single-Axis Rotation Ring Laser Gyroscope SINS

LIU Yong-hong1, LIU Ming-yong1, XIE Bo2
(1. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China; 2. The 16 Re -search Institute of the 9th Academy, China Aerospace Science and Technology Corporation, Xi′an 710100, China)

An alignment scheme for single-axis rotation ring laser gyroscope(RLG) strapdown inertial navigation system (SINS)is designed, and the error parameters of the inertial device affecting the alignment accuracy are analyzed. The alignment scheme is validated by simulation, and the different errors of inertial devices corresponding to the alignment accuracy are compared. Simulation result indicates that the scale factor asymmetry error and the scale factor error of the vertical axis gyro exert significant effects on the alignment accuracy of course angle. This study may offer a reference for design of single-axis rotation RLG SINS.

strapdown inertial navigation system; alignment accuracy; inertial device; scale factor

TJ630.33; U666.1

A

1673-1948(2014)02-0115-06

2013-10-25;

2014-02-18.

刘永红(1981-), 女, 在读博士, 高级工程师, 主要研究方向为惯性导航技术.