超空泡航行体通气规律数值仿真
2014-06-05孙士明陈伟政
孙士明, 颜 开, 陈伟政
(中国船舶科学研究中心 水动力学重点实验室, 江苏 无锡, 214082)
超空泡航行体通气规律数值仿真
孙士明, 颜 开, 陈伟政
(中国船舶科学研究中心 水动力学重点实验室, 江苏 无锡, 214082)
为了研究针对高傅汝德数(Fr数)下超空泡航行体通气规律问题, 基于 RANS方程, 采用流体体积函数(VOF)多相流模型对小空化数下超空泡航行体通气规律进行仿真, 分析了通气空化条件下空泡内的流场速度及压力分布, 对比不同通气率条件下的空泡形态及空泡壁面压力分布, 得出了不同自然空化数和雷诺数(Re数)条件下超空泡通气规律, 仿真结果与试验现象一致。基于仿真结果与量纲分析, 针对高Fr数下通气超空泡, 给出了考虑自然空化数影响的通气系数计算公式, 可为进一步研究人工超空泡通气规律提供参考。
超空泡航行体; 空化; 通气率; 流体体积函数; 数值仿真
0 引言
通气超空泡技术是指利用人工通气的方式使水下航行体周围完全被气体包裹, 从而大幅降低阻力。为了维持航行体获得稳定航行所需要的流
体动力, 需要保证空泡具有稳定的尺度, 即必须保证空泡内相应的气体含量, 这就需要连续稳定地向空泡内通气。通气率的大小是控制空泡形态的重要参数, 它受到多参数的影响。
由于通气超空泡涉及很多复杂理论, 目前对通气规律的理论研究多是在大量试验数据基础之上归纳总结得到的。Logvinovich和Spurk针对高傅汝德数(Fr数)下的通气超空泡通过量纲分析和试验研究分别得到了相应的通气率计算经验公式[1-2]。随着计算机的发展, 数值仿真可以很好地解决一些理论和试验上的困难, 对超空泡研究的手段进行补充。Kunz等人基于均值平衡流模型发展了一套完整的超空泡流动计算程序, 可计算自然空化和通气空化流场等[3]。Kinzel等人在 Kunz基础上分别引入分离涡模拟和标准双方程湍流模型, 仿真了迟滞效应影响下的空化数随通气率的变化规律[4]。国内文献多是在商业软件基础上对通气空泡进行研究, 大多采用均质混合多相流模型, 而且公开的文献中对通气规律的研究比较少。陈鑫等在流体体积函数(volume of fluid, VOF)多相流模型框架内进行了 2D水翼的通气空泡气液两相流动的数值仿真[5]。周景军利用分相流模型仿真了低Fr数和通气率条件下的空泡泄气率[6]。以上研究均集中在中低Fr数范围内, 而且对影响通气率的因素大多仅考虑Fr数, 但实际情况中超空泡航行体往往是在高 Fr数和小空泡数下航行,因此很有必要对高Fr数下的航行体通气规律及影响通气率的因素问题展开系统研究。
本文采用 VOF多相流模型, 并耦合自然空化模型, 针对高 Fr数下的航行体超空化流场进行数值仿真, 分析了不同条件下通气系数对航行体空泡形态的影响, 并重点研究了自然空化数和雷诺数(Re数)对通气率的影响。
1 数学模型和计算方法
1.1 控制方程
采用如下控制方程

假设流动过程绝热等温, 则无需引入能量方程。针对气体的可压缩性, 还需求解理想气体的状态方程

1.2 空化模型
本文计算采用 Zwart空化模型, 该模型是基于 Rayleigh-Plesset气泡动力学方程发展出来的,得到蒸发和凝结相的表达式分别为

式中:RB表示气泡半径;Fc和Fe分别为蒸发和凝结常数项;pv为气泡压力;p为环境压力。
1.3 湍流模型
计算采用标准k-ε湍流模型[7]
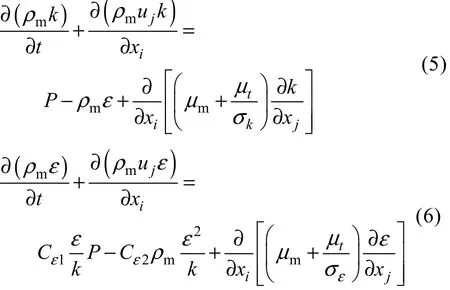
1.4 计算网格与边界条件
计算模型为装有圆盘空化器的轴对称体。前段为圆锥体, 后段为圆柱体, 空化器直径 8 mm,后体圆柱段直径40 mm, 模型总长550 mm。模型头部装有2个通气碗, 前后2处通气孔宽度均为1 mm。计算采用2D轴对称模型, 整个计算域为3700mm× 500mm, 采用四边形结构化网格划分。图1和图2为网格划分情况及边界条件。外流场的进出口设置为压力入口和压力出口, 两侧为不可滑移壁面边界条件, 通气孔设置为质量流量入口。

图1 计算网格与边界条件Fig. 1 Computation mesh and boundary condition

图2 模型头部放大示意图Fig. 2 Schematic of partially enlarged model head
本文的计算采用有限体积法对控制方程进行离散, 利用SIMPLE算法进行压力速度耦合。动量方程和湍流输运方程的差分格式均采用2阶迎风格式。
2 计算结果与分析
2.1 与试验对比验证


图3 不通气条件下空泡形态比较Fig. 3 Comparison of cavity shapes without ventilation

图4 通气条件下空泡形态比较Fig. 4 Comparison of cavity shapes with ventilation
2.2 通气超空泡流场分析
通气空泡与自然空泡一个明显的差别就是,通气空泡内的气体会不断向下游流动, 并从空泡尾部泻出, 因此, 了解空泡内气体流动状态对通气规律的研究具有重要意义。图5显示了航行体形成超空泡后的流场压力分布。可以看出, 当超空泡形成后会在航行体周围形成一个低压区。靠近空化器的下游区域压力最低, 尾部空泡闭合处压力最高, 整个空泡内的压力并不完全恒定, 而是呈现缓慢上升的趋势。这种趋势从图6中的沿空泡壁面和航行体壁面的压力系数曲线可以看得更为清晰。在航行体圆锥段, 压力上升较为明显;而在航行体圆柱段, 压力基本保持不变; 当空泡壁面越过整个航行体后, 空泡的闭合使压力又迅速提升。空泡壁面和航行体壁面都显示了相同的趋势, 可以认为空泡内的压力在径向基本保持不变, 仅沿轴向变化。

图5 超空化流场压力分布Fig. 5 Pressure distribution of supercavitating flow field

图6 空泡壁面及航行体壁面压力系数曲线Fig. 6 Pressure coefficient curves of cavity wall and vehicle wall
图7显示了空泡首尾部的流线图, 从中可以看出气体从通气孔流出后的走向。航行体头部结构的复杂性使得空泡头部流动较为复杂, 可以看出, 从前部通气孔流出的气体一部分向圆盘空化器头部低压区流动, 随后受外流场影响沿空泡壁面与该通气孔流出的另一部分气体汇合, 一起向下游流动; 从后通气孔流出的气体受空泡内回流气体的作用, 在流动一段距离后流向空泡壁面附近并沿空泡壁面向下游流动。除空泡头部存在若干涡结构外, 在航行体圆锥段部分存在一个环流结构, 当空泡发展到航行体圆柱段时, 由于空泡壁面与航行体之间流动通道的突然减小, 这种环流流动形式不再存在, 气体全部向下游流动。在航行体尾部, 由于空泡壁面与航行体相对位置的突变, 存在与空泡首部类似的环流流动结构。气体主要沿空泡壁面向下游流动, 在空泡尾端, 一部分气体由尾部泻出, 一部分则回流进空泡。由以上分析可以看出, 空泡壁面会对空泡内气体流动产生重要影响, 这也是造成空泡内沿轴向压力变化的重要原因之一。

图7 空泡首尾部流线图Fig. 7 Streamlines in front and back of cavity
以上对空泡内的流场分析仅针对某一工况,当通气率变化时, 空泡形态也会随之变化。图 8显示了不同通气系数条件下的空泡形态变化规律,计算中的自然空化数控制为 0.18。可以看出, 通气率对空泡形态影响显著。小通气率条件下, 航行体无法生成超空泡, 空泡尾部闭合点无法越过航行体, 造成尾部的不稳定泄气; 当通气率增加到一定值时, 空泡闭合在航行体后, 可以形成稳定超空泡; 此后, 继续增加通气率, 空泡最大直径变化不大, 但会导致空泡尾部流场发生变化。

图8 不同通气系数下空泡形态比较Fig. 8 Comparison of cavity shapes with different ventilation coefficients
图 9为不同通气系数条件下的空泡壁面压力分布, 图中的通气系数均可保证航行体生成超空泡。可以看到, 随着通气系数的增加, 空泡壁面沿轴向的压力变化趋于平缓。这种变化在航行体圆锥段和尾部表现得更为明显, 而在航行体圆柱段, 空泡壁面沿轴向压力仅随通气率的提高略微增加。

图9 不同通气系数下空泡壁面压力系数曲线Fig. 9 Pressure coefficient curves of cavity wall with different ventilation coefficients
2.3 自然空化数对通气率的影响
自然空化数的改变可以通过改变来流速度或环境压力来实现。本文通过保持来流速度不变而改变环境压力来探究不同自然空化数对通气率的影响, 这样做可以保证除自然空化数外的其他参数不变。图10和图11分别为不同自然空化数条件下通气系数随通气空化数变化曲线和阻力系数随通气系数变化曲线。可以看出, 在不同自然空化数下, 通气空化数均随通气系数增加而降低,但随着自然空化数的降低, 相同通气空化数下的通气系数也随之降低, 即形成相同尺寸的空泡,自然空化数越小时所需的通气系数也越小。这种规律同样可从阻力系数曲线中看出, 相同通气系数下, 低自然空化数时的阻力系数也相对较低;随着通气系数的逐渐增加, 低自然空化数时, 阻力系数最先达到最小值, 即形成稳定的超空泡。
2.4 Re数对通气率的影响
Re 数的改变往往伴随着Fr数的改变。为了分析 Re数对通气系数的影响, 本文计算了空化器直径分别为8 mm和17 mm 2种尺度下的通气超空泡, 通过改变2种尺度工况下的来流水速和环境压力, 保证仅 Re数不同而自然空化数和 Fr数均相同。图12和图13分别为不同Re数条件下通气系数随通气空化数变化曲线和阻力系数随通气系数变化曲线。可以看出, Re数对通气系数的影响并不明显, 部分空化数区域, 曲线甚至重合。通气系数较小时, Re数增大会使阻力系数增大, 当通气系数增大至形成超空泡后, 2种Re数下阻力系数变化规律基本一致。因此可以认为通气系数是Re数的弱函数。

图10 不同自然空化数下通气系数随通气空化数变化曲线Fig. 10 Curves of ventilation coefficient versus ventilation cavitation number for different natural cavitation numbers
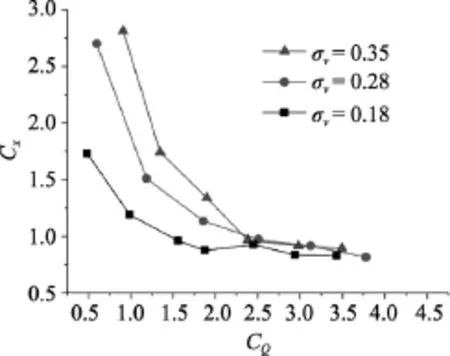
图11 不同自然空化数下阻力系数随通气系数变化曲线Fig. 11 Curves of drag coefficients versus ventilation coefficient for different natural cavitation numbers
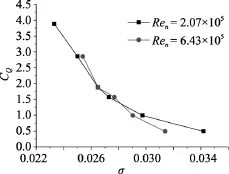
图12 不同Re数下通气系数随通气空化数变化曲线Fig. 12 Curves of ventilation coefficient versus ventilation cavitation number for different Reynolds numbers
3 通气系数经验公式修正
超空泡流动涉及到多相流、湍流、可压缩性等流动机制, 这使通气率的研究变得极为复杂。量纲分析可以使这一问题得到简化, 因而被广泛接受。考虑通气率与来流水速与空泡尺度(空泡长度、空泡中截面直径)有关, 通过量纲分析可得

图13 不同Re数下阻力系数随通气系数变化曲线Fig. 13 Curves of drag coefficient versus ventilation coefficient for different Reynolds numbers

式中,CD0为空化器零空化数下的阻力系数。Spurk认为当常数值取为0.013时, 该公式可应用于绝大多数工程情况[2]。
实际上, 该常数值受到σv, Fr数, 韦伯数(We数)和Re数等多个参数的影响。考虑高Fr数下的稳定超空泡, 可将Fr数和We数的影响忽略。由前面计算结果可知, 通气系数受自然空化数影响较大, 受Re数影响很小。因此, 将上述公式的常数值加入一项自然空化数影响因子, 即

式中, 自然空化数影响因子中的n表征自然空化数的影响程度。通过与之前计算结果比对, 发现当n= 2, const = 0.0001时, 不同自然空化数下的各条曲线与计算结果符合良好, 这也从另一方面验证了该公式的可行性。图14为不同自然空化数下基于量纲分析的公式与数值计算结果对比。

图14 通气系数修正公式与数值计算结果比较Fig. 14 Comparison of ventilation coeff icients from both modified formula and numerical calculation
4 结论
本文采用VOF多相流模型针对高Fr数下超空泡航行体的通气规律进行了数值仿真, 得到了如下结论。
1) 通入空泡内的气体均沿壁面向下游流动,并在航行体圆锥段和尾部形成环形流动结构, 可以认为空泡壁面对超空泡的泄气有重要影响。空泡内压力沿轴向逐渐升高, 沿径向基本保持不变。这种压力变化随通气率的增加而减小。
2) 空泡尺度随通气率增加而增加, 当通气率达到一定程度后, 空泡尺度基本保持不变, 再增加通气率, 只会导致尾部流场发生变化。
3) 自然空化数越小, 形成相同尺度空泡所需的通气系数也越小; Re数对通气系数的影响较自然空化数要小, 可认为是通气系数的弱函数。
4) 基于通气系数的量纲分析, 考虑自然空化数的影响, 提出了计算通气系数的修正公式,与计算数据进行拟合比较, 一致性良好。
[1] Logvinovich G V. Hydrodynamics of Flows with Free Boundaries[M]. Kiev: Naukova Dumka Publishing, 1969.
[2] Spurk J H. On the Gas Loss From Ventilated Supercavities[J]. Acta Mechanica, 2002, 155(3-4): 125-135.
[3] Lindau J W, Kunz R F, Mulherin J M, et al. Stinebring, Fully Coupled 6-DOF to Uran s Modeling of Cavitating Flows Around a Supercavitating Vehicle[C]//CAV2003, Osaka, Japan, 2003.
[4] Kinzel M P, Lindau J W, Peltier J, et al. Computational Investigations of Air Entrainment, Hysteresis, and Loading for Large-scale, Buoyant Cavities[C]//Pittsburgh: DoD High Performance Computing Modernization Program Users Group Conference, 2007.
[5] 陈鑫. 通气空泡流研究[D]. 上海: 上海交通大学, 2006.
[6] 周景军. 低弗鲁德数条件下通气超空泡泄气机理数值模拟[J]. 工程力学, 2011, 28(1): 251-256.
Zhou Jing-jun. Numerical Si mulation of Gas Leakage Mechanism of Ventilated Supercavity Under the Condition of Low Froude Number[J]. Engineering Mechanics, 2011, 28(1): 251-256.
[7] Launder B E, Spalding D. The Numerical Computation of Turbulent Flows[J]. Computer Methods in Applied Mechanics and Engineering, 1974, 3: 269-289.
(责任编辑: 陈 曦)
Numerical Simulation of Ventilation Law for Supercavitating Vehicle
SUN Shi-ming, YAN Kai, CHEN Wei-zheng
(National Key Lab of Science and Technology on Hydrodynamics, China Ship Scientific Research Center, Wuxi 214082, China)
To understand the ventilation law of a supercavitating vehicle in high Froude number flows, RANS equations and the volume of fluid (VOF) multiphase flow model are employed to simulate the ventilation law of a supercavitating vehicle in the case of small cavitation number. The distributions of velocity and pressure in ventilated supercavitationflow are described. The cavity shapes and the pressure along the cavity wall with different ventilation rates are compared, respectively. The ventilation laws at different natural cavitation number and Reynolds number are obtained, and simulation results agree well with experimental phenomena. Based on the calculation results and the dimension analysis, a new formula considering the influence of natural cavitation number is proposed to calculate the ventilation coefficient at high Froude number.
supercavitating vehicle; cavitation; ventilation rate; volume of fluid; numerical simulation
TJ630.1; U661.1
A
1673-1948(2014)02-0081-06
2014-01-01;
2014-01-21.
孙士明(1988-), 男, 在读硕士, 研究方向为空泡水动力学.
