光纤水听器PGC解调归一化参数实时估计方法
2014-06-05周少玲贠晓辉
周少玲, 贠晓辉
(1. 中国电子科技集团公司 第23研究所, 上海, 200437; 2. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710075; 3. 水下信息与控制重点实验室, 陕西 西安, 710075)
光纤水听器PGC解调归一化参数实时估计方法
周少玲1, 贠晓辉2,3
(1. 中国电子科技集团公司 第23研究所, 上海, 200437; 2. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710075; 3. 水下信息与控制重点实验室, 陕西 西安, 710075)
针对光纤水听器相位生成载波(PGC)相位解调中采用离线估计归一化参数进行处理带来的明显失真, 提出了一种归一化参数实时估计方法。该方法通过先计算2路正交信号目前时间点信号幅度与前一时间点信号幅度平方差, 再计算两者比值得到归一化参数。通过仿真结合试验测量, 验证了该方法可以在较小信号幅度情况下实现准确的归一化参数估计。试验结果表明, 当光纤水听器上施加峰值为0.3 rad的信号时, 采用实时估计的归一化参数值估计误差小于3%, 用该值进行光纤水听器信号解调处理, 得到的信号与总谐波失真比优于48 dB, 可满足工程化应用需要。
光纤水听器; 相位生成载波; 参数实时估计; 总谐波失真
0 引言
光纤水听器具有无需水下供电, 易于构成大规模阵列, 能够适应恶劣环境等优点, 在海洋环境监测、安全防御和资源勘探等领域有着广泛的应用[1-3]。干涉型光纤水听器利用双光束干涉原理,将环境声压变化转换为光纤中光相位变化, 通过信号处理系统提取声信号信息。外界环境扰动引起干涉仪初相位随机漂移, 当相位为π/2及其整数倍时将出现相位信号衰落。从干涉信号中准确提取被测信号的解调技术是光纤水听器研究的组成部分。表征信号解调技术性能的指标主要包括解调结果的准确性、稳定性、噪声水平、动态范围、成本以及复杂度等。
被动零差法是目前应用较为广泛的光纤水听器信号解调方法, 包括3×3耦合器检测法和相位生成载波(phase generated carrier, PGC)法。3×3耦合器检测法是一种简单零差法, 利用3×3耦合器3路输出间具有固定相位差的特点, 通过3路输出信号间的运算进行解调处理解决干涉信号的相位衰落[4]。这种方案不需载波调制, 不存在载波频率太低导致的各次谐波频带混叠的问题, 解调信号动态范围大, 理论上可实现等臂干涉。该方法缺点是低频噪声高, 信号处理端结构复杂, 对大规模时分、波分复用系统来说, 分波器、光电转换器、模数转换器等各种器件均以3倍的数量增加,不利于实际工程应用中关心的低功耗、小型化。采用2路输出信号解调可在一定程度上简化系统结构, 但输入光功率变化将导致解调结果失真。以非干涉脉冲作参考进行光强补偿的方案可以在一定程度上缓解光功率变化导致的信号失真[5]。
PGC法是将所要检测的传感信号调制在载波上, 利用奇次载波频率上的边带信号衰落则偶次载波频率上的边带信号一定不衰落的原理解决干涉信号的信号衰落[6]。PGC法的特点是低频噪声低, 信号处理端结构简单, 一路信号就可以解调。相位产生载波调制后的信号是一种调相信号, 其
特征是频带与信号频率和幅度都有关, 高频率大幅度的信号占用很宽的频带。实践证明, 为充分满足动态范围要求, 使各次倍频的频带不混叠,实现高保真解调被检测信号, 往往要求载波频率是检测信号的几十倍甚至上百倍。目前常用的相位产生载波调制无论内调制还是外调制, 引入的载波频率为几十千赫兹, 可以满足几千赫兹水声信号动态范围解调的要求。
光纤水听器信号解调处理一般采用交叉相乘法或反正切法得到与传感信号成正比的相位变化。为得到准确、稳定的解调结果, 在进行交叉相乘或反正切处理之前都必须对信号进行归一化处理, 使之具有相同的幅度。目前常用的归一化参数估计方法需要预先在水听器上施加信号, 通过观察至少一个2π周期的相位变化, 得到输入信号的峰值, 以这些参数作为基础进行水听器信号解调[7]。在实际使用中, 2π弧度相位变化的参数估计条件有时难以满足, 另外系统光强波动、干涉条纹可见度变化等导致系统参数发生变化, 使预先估计的这些参数在信号解调中产生明显失真。
本文提出一种PGC解调参数实时估计方法,可以在较小信号幅度情况下实现准确的参数估计。采用Labview对解调参数实时估计进行数值仿真, 得到参数估计误差与信号幅度的关系, 通过试验对仿真结果进行了验证。
1 算法原理
PGC解调所需的载波可通过压电陶瓷锆钛酸铅(PbZrTiO3, PZT)调制干涉仪或直接调制光源频率来获得。干涉型光纤水听器的干涉仪输出光信号经光电探测器转换为电信号, 其输出为

式中: A(t)为干涉光强直流项; B(t)为干涉光强交流项, 与干涉仪的输入光强、光纤耦合器的分光比、2束干涉光的偏振态等参数有关; C为相位调制深度; ω为调制频率;φi为干涉信号中i倍频载波分量与本地同频载波信号之间的固定相位差,与光路延迟、电路延迟等因素有关; ϕs(t)为光纤水听器需要检测的信号; Ji(C)是以C为变量的i阶第1类贝塞尔函数。
PGC解调处理流程如图1所示, 本地乘法单元产生1倍频载波和2倍频载波信号, 其表达式表示为

干涉信号经模数转换与1倍频载波和2倍频载波混频, 再经过低通滤波器滤除载波及高频分量,得到含有被检测信号信息的2个正交分量


图1 相位生成载波(PGC)解调原理框图Fig. 1 Principlie of phase generated carrier(PGC) demodulation
被检测信号的值通过计算V1(t)/V2(t)比值的反正切得到。为了在反正切运算得到正确的被检测信号, V1(t)和V2(t)的值通过归一化设定为相等幅度。在理想情况下, 将相位调制深度C设定为2.63 rad, 使J1(C)= J2(C), 并通过预先测算得到1倍频和2倍频载波频率信号相位差ϕ1和ϕ2, 对cosϕ0和cos2ϕ0的幅度进行修正, 达到归一化目的。但在复用调制器件的光纤水听器阵列中, 由于伴生光强调制或PZT响应的迟滞效应等原因,难以保证每个光纤水听器的干涉信号载波调制度C都为2.63 rad。干涉信号载波与本地载波信号之间的相位差随传输光纤长度、电路参数的不同而改变, 光纤器件受应力等因素影响, 直流光强、交流光强也会发生变化, 因此实验室调试环境下预先测算的固定参数与实际使用参数不会完全相同。在实际环境中, 由于温度、应力等变化比例因子变化可达10%甚至更多。归一化参数估计不准将使水听器检测信号稳定性和精度降低, 谐波分量增加。
在文中将C, ϕ1, ϕ2的影响看成一个整体, 估计方程式(3)中方括号内项的比值作为归一化参数用于解调处理。由于采样过程中的各种噪声和误差, 为了提高参数估计的可靠性, 采用比较多的数据来估计解调参数。图2为PGC信号检测数字化归一化参数实时估计过程。低通滤波后得到连续采样点的正交分量V1和V2, 利用V1和V2各分别组建2组具有相同变化规律的数组V1m(i), V1n(i)和V2m(i), V2n(i), 其中m(i), n(i)表示组建数组时选择的特定采样信号, i为连续采样点V1和V2的序号。分别计算其对应的DV1i, DV2i


图2 实时参数估计流程图Fig. 2 Flow chart of real-time parameter estimation
对N个DV1i, DV2i求和

在计算V1N, V2N比值的过程中, 为了将比值控制在不大于1的范围内, 采用下式进行计算

计算两正交分量的归一化值
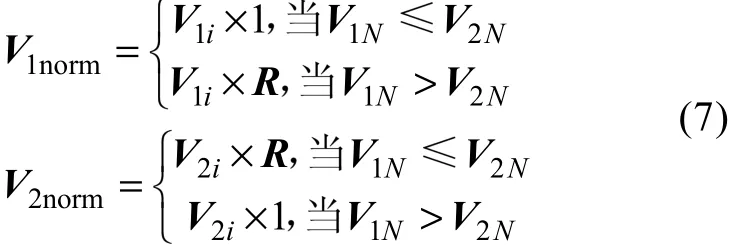
按以上程序, 不断循环实时估算两正交分量的归一化值, 一方面可实时更新定标数据, 另一方面可提高参数估计的可靠性, 消除由于采样过程中的各种噪声和误差造成的估计不可靠, 该方法的优点是不需标定即可实现传感信号的实时解调。
2 Labview 仿真
表征光纤水听器解调方法性能的指标有很多,本文主要研究归一化参数估计误差对解调幅度稳定性和信号与总谐波失真比的影响。解调幅度稳定性规定为解调输出信号幅度与输入信号幅度的比值(单位为dB), 是评价解调系统可靠性的重要指标。本文中, 信号与总谐波失真(total harmonic distortion, THD)比规定为信号功率与总谐波功率的比值, 是评价解调系统失真度的重要指标。THD值越大, 解调非线性失真越小。
采用Labview对归一化参数估计方法进行仿真, 仿真参数设置为: 相位调制深度2.63 rad, 1倍频和2倍频载波与本地载波初始相位差ϕ1和ϕ2为零, 采样率200 kS/s, 采样点数200 k, 持续时间1s,电路噪声峰峰值5 mV。干涉信号中存在环境温度应力等因素引起的1.5 Hz低频相位漂移。图3为THD与归一化误差关系仿真结果。归一化误差小于3%时, THD在45 dB以上。
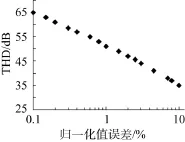
图3 信号与总谐波失真(THD)比与归一化参数估计误差关系Fig. 3 Relationship between signal to total harmonic distortion ratio and estimation error of normalized parameter
信号频率为100 Hz, 峰值信号幅值为0.1 rad时, 采用以上估计方法得到的归一化参数估计值与标称值之间估计误差最大值约为 11.4%。峰值信号幅值为 0.2 rad 时, 估计误差最大值约为4.32%。峰值信号幅值为0.3 rad时, 估计误差最大值约为2.42%。峰值信号幅值为0.4 rad时, 估计误差最大值约为1.0%。随着信号幅值的继续增加, 估计误差最大值基本不变或继续减小。仿真结果表明, 信号幅度是决定估计误差的主要参数,当信号幅度小于0.2 rad时, 归一化参数估计误差较大, 随着信号幅度增加, 归一化参数估计误差下降, 当信号峰值在0.3 rad及以上时归一化值估计误差最大值可达到小于3%。
仿真比较了10 Hz, 100 Hz和1 000 Hz这3种信号频率下, 不同信号幅度与归一化参数实时估计值与理论值误差关系, 仿真结果见图4。在不同频率下, 归一化参数估计误差与m(i), n(i)和N的设置有关。信号频率为10 Hz, m(i)与n(i)的差值设为400, N设为800。信号频率为100 Hz, m(i)与n(i)的差值设为100, N设为300。信号频率为1 000 Hz, m(i)与n(i)的差值设为20, N设为200。仿真结果表明, 为降低估计误差, 需要根据不同频率情况调整m(k), n(k)和N的设置。

图4 信号幅值与归一化参数估计误差关系Fig. 4 Relationship between signal amplitude and normalized parameter estimation error
3 试验验证
试验采用光程匹配干涉仪的PGC相位解调时分复用传感系统结构, 原理框图如图5所示。传感器和光程匹配干涉仪的结构一致, 由2×2耦合器和2个法拉第旋镜(Faraday rotator mirror, FRM)组成不平衡迈克尔逊干涉仪, 参考臂和传感臂的臂长差为Δl, 法拉第旋镜用于消除干涉信号的偏振衰落, 光纤线圈缠绕在PZT上, 匹配干涉仪上的PZT用来引入解调处理时需要的调制载波信号,传感器上的PZT用来引入模拟传感信号。
激光器发出的光经声光调制器(acoustic optical modulator, AOM)调制为脉冲光, 光脉冲的宽度为传感器臂长差对应的往返时间。脉冲光经过可调光衰减器(variable optic Attenuation, VOA)和传输光纤进入传感器。传感器返回2个在时域上互不重叠的脉冲光。经过光程匹配干涉仪后, 在时域上得到3个光脉冲, 中间脉冲为携带传感信息的干涉光脉冲。干涉光脉冲信号经过光电探测器(photo diode, PD)转换为电脉冲信号, 进入高速数数据采集控制电路, 现场可编程门阵列(field programmable gate arrays, FPGA)控制14位模数转换器(analog digital convertor, ADC)以300kS/s采样率对干涉脉冲进行采样, 同时产生AOM的驱动脉冲、PZT的调制载波以及同步采样控制信号实现对时分复用干涉脉冲的同步采集, 调制载波设置为30 kHz, 相位调制深度设置为2.63 rad。

图5 试验原理框图Fig. 5 Block diagram of experimental principle
试验中, 采用FPGA和Labview软件编写数据采集、处理、显示程序, 采集的干涉信号经混频低通滤波后, 利用上述介绍的实时参数估计法得到解调参数, 然后采用反正切法对传感器信号进行解调, 高通滤波滤除环境温度变化等产生的低频漂移。作为对比, 同时利用常规离线参数估计和反正切法对传感器信号进行解调。在PZT上加载160 Hz单频电压信号。当传感器产生3.14 rad的相位变化时, 在10 000次测量中, 实时估计法得到的解调信号幅度起伏小于0.1 dB(如图6所示),信号与总谐波失真比为48~56 dB(如图7所示), 与离线参数估计法得到的解调结果相当。

图6 解调信号幅值Fig. 6 Amplitude of demodulated signal
4 结束语
参数估计是光纤水听器数字信号解调的一个关键环节, 目前通常采用离线参数估计方法,实际系统光强波动、干涉条纹可见度变化等导致离线估计参数在信号解调中产生明显失真。本文提出光纤水听器相位生成载波解调参数的实时估计方法, 可有效消除参数变化对解调结果的影响,通过仿真和试验验证了该方法的有效性。当传感器产生3.14 rad的相位变化时, 在10 000次测量中, 实时估计法得到的解调信号幅度起伏小于0.1 dB, 信号与总谐波失真比为48~56 dB, 与离线参数估计法得到的解调结果相当。

图7 解调信号THDFig. 7 Curve of demodulated signal to total harmonic distortion ratio
[1] Kirkendall C K, Dand ridge A. Overview of High Performance Fibre-optic Sensing[J]. Journal of Physics D: Applied Physics, 2004, 37(4): 197-216.
[2] Wooler J P, Crickmore R I. Fibre Optic Sensors for Seismic Intruder Detection[C]//17th International Conference on Optical Fiber Sensors, 2005, SPIE.
[3] Juarez J C, Maier E W, Nam C K, et al. Distributed Fiber-optic Intrusion Sensor Sy stem[J]. Journal of Lightwave Technology, 2005, 23(6): 2081-2087.
[4] Priester G. Analysis of Fiber Interferometer Utilizing 3×3 Fiber Coupler[J]. IEEE Journal of Quantum Electronics, 1982, 18(10): 1601-1603.
[5] 张华勇, 王东宁, 施清平, 等. 基于 3×3耦合器的光纤水听器时分复用系统的光强补偿方法[J].中国激光, 2011, 38(11): 174-181.
Zhang Hua-yong, Wang Dong-ning, Shi Qing-ping, et al. Optical Intensity Compensating Method for Time Division Multiplexing of Fiber-optic Hydrophone Using a 3×3 Coupler[J]. Chinese Journal of Lasers, 2011, 38(11): 174-181.
[6] Dandridge A, Tvelen A B, Glallorenzi T G. Homodyne Demodulation Scheme for Fiber Optic Sensors Using Phase Generated Carrier[J]. IEEE Journal Quantum Electronic Letter, 1982, 18(10): 1647-1653.
[7] 施清平, 王凯, 王利威, 等. 基于参数估计的光纤水听器解调系统研究[J]. 仪器仪表学报, 2011, 32(8): 1864-1870.
Shi Qing-ping, Wang Kai, Wang Li-wei, et al. Optical Fiber Hydrophone Demodulation System Based on Parameter Estimation Method[J]. Chinese Journal of Scientific Instrument, 2011, 32(8): 1864-1870.
(责任编辑: 杨力军)
Real-time Estimation Method of Normalized Parameter for PGC Demodulation of Optical Fiber Hydrophone
ZHOU Shao-ling1, YUN Xiao-hui2,3
(1. The 23 Research Institute, China Electronics Technology Group Corporation, Shanghai 200437, China; 2. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 3. Science and Technology on Underwater Information and Control Laboratory, Xi′ an 710075, China)
A real-time estimation method of normalized parameter is proposed to reduce the significant distortion in phase generated carrier(PGC) demodulation of optical fibe r hydrophone due to offline estimation of normalized parameter. The square differences of the amplitudes of two orthogonal signals at both current time point and previous time point are calculated, then the normalized parameter is obtained by calculating the ratio of two square differences. Simulations and experiments show that a correct normalized parameter can be achieved with the proposed method if signal amplitude is small. Experimental results indicate that when a small signal with peak amplitude of 0.3 radian is imposed to the hydrophone, the estimation error of normalized parameter gets less than 3%. Using the achieved normalized parameter to demodulate the signal of the optical fiber hydrophone, signal to total harmonic distortion ratio is less than 48 dB, which meets the requirement for engineering application.
optical fiber hydrophone; phase generated carrier; real-time parameter estimation; total harmonic distortion
TJ630.34; TP212.14
A
1673-1948(2014)02-0091-05
2013-10-14;
2013-11-18.
周少玲(1966-), 女, 硕士, 高级工程师, 主要从事光纤传感器系统和光电信号处理技术研究.
