一种宽带脉冲串信号模糊度函数实现方法

岳 雷, 梁 红, 杨长生

(西北工业大学 航海学院, 陕西 西安, 710072)

一种宽带脉冲串信号模糊度函数实现方法

岳 雷, 梁 红, 杨长生

(西北工业大学 航海学院, 陕西 西安, 710072)

宽带脉冲串信号的模糊度函数是信号分析、波形设计的有力工具以及检测估计常用的方法, 实现宽带脉冲串信号的模糊度函数首先要合成副本, 直接复制尺度伸缩后的子脉冲并乘以不同的权系数来合成副本时, 会导致大多数副本向量中信息移位和缺失。针对这一问题, 采取了对整个脉冲串压缩后再重采样的方法来合成副本信号, 并进行了仿真验证。仿真结果表明, 该方法具有可行性和实用性, 为宽带脉冲串信号模糊度函数的实现提供了参考。

脉冲串信号; 模糊度函数; 副本; 重采样

0 引言

相比单个脉冲信号而言, 脉冲串信号具有明显的优点: 既保留了脉冲信号高距离分辨力的优势, 又有连续波信号高速度分辨力的特点; 其可控参数多, 便于作为自适应控制信号; 在不增加带宽的前提下, 靠增加子脉冲个数来增加总的信号持续时间, 其模糊度函数图通过编码等技术几乎可以做成任意形式。线性调频脉冲串(pulse trains of linear frequency-modulated waveforms, PTFM)[1]信号是在线性调频信号和频率步进编码信号的基础上发展起来的。采用脉内线性调频,脉间载频步进的方式获得更大的时宽带宽积和信号持续时间, 通过后处理获得更高的距离分辨力和速度分辨力。其模糊度函数呈钉板型, 中心模糊区呈图钉型, 具有很高的距离和速度分辨力。与线性调频信号相比, 降低了发射和接收通道的瞬时带宽[2]。

对于大多数无线电和雷达系统应用来说, 采用窄带作近似处理是足够准确的, 而对于声纳和其他语音系统来说这种近似却不够准确甚至会造成错误[3-4]。文献[5]分析了宽带模糊度函数和窄带模糊度函数的差异, 对运动目标来说, 宽带信号带宽内不同频率有不同的频移, 其模糊度函数中的发射信号和副本信号只能用复信号形式, 不能再用复包络代替, 而原先窄带信号模糊度函数中的多普勒频移在宽带信号情况下变成了尺度伸缩, 尺度的伸缩不仅导致信号频率的伸缩, 而且导致了信号时宽的伸缩, 从而导致窄带模糊度函数和宽带模糊度函数实现方法的不同。

由宽带信号模糊度函数定义可知[5], 它是发射信号和副本信号的相关输出绝对值的平方。宽带脉冲串信号是由许多段调频信号组成的, 实现其模糊度函数时, 首先要合成副本信号(发射信号可看作是副本信号中尺度为1的一个特例)。对于副本信号来说, 尺度伸缩导致信号的时宽、带宽和中心频率等发生变化, 因此在合成副本信号时应特别注意的是, 需要对整个脉冲串压缩后再重采样来合成副本, 本文以线性调频脉冲串信号为例, 仿真实现其模糊度函数。

1 宽带脉冲串信号

宽带脉冲串信号形如

其中:A(n)是信号包络;p(n,t,f)是每一小段调频信号, 调频信号是n、时间t和频率f的函数。下面以线性调频脉冲串信号为例, 说明其合成过程。

PTFM信号的表达式如下

其中

式(3)即为线性调频信号。

图1 线性调频信号时域图Fig. 1 Time domain diagram of Linear frequency-modulated signal

图2 线性调频脉冲串信号时域图Fig. 2 Time domain diagram of linear frequency- modulated pulse train signal

2 PTFM信号模糊度函数

宽带模糊度函数是没有噪声情况下宽带相关处理的全景输出, 宽带自模糊度函数描述信号与经过尺度伸缩和时间延迟的信号间的相关度量,宽带互模糊度函数对应的是接收信号为经尺度伸缩和时间延迟的发射信号的宽带相关处理器的输出。以下以宽带自模糊度函数为工具说明 PTFM信号模糊度函数实现过程。

式中

为宽带模糊函数或宽带不确定性函数[6]。

由相关定理

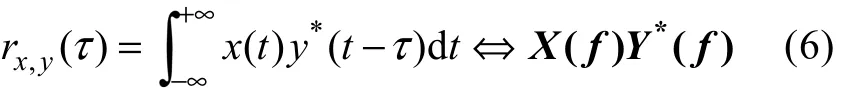
可知, 时域的相关经过傅里叶变换后等于频域的共轭相乘[7]。

图3是模糊度函数实现流程图, 根据图3把实现模糊度函数分为3个步骤: 1) 根据提前设定好的尺度范围确定总的副本个数; 2) 合成发射信号和副本信号; 3) 采取基于快速傅里叶变换(fast Fourier transform, FFT)的快速处理方法得PTFM信号的模糊度函数。

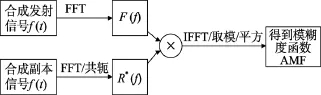
图3 模糊度函数实现流程图Fig. 3 Flow chart of ambiguity function realization

如引言部分所述, 发射信号可以看作是副本信号的一个特例, 下面就直接以具有通用性的副本信号合成为例, 说明本文合成副本信号的过程。

本文合成副本信号的方法: 整体的思想是对整个脉冲串经过尺度伸缩后重采样。

具体实现为: 总体分 2种情况, 第 1种情况是某个尺度值下压缩的子脉冲持续时间结束点处刚好被采样到; 第2种情况是某个尺度值下压缩的子脉冲持续时间结束点处不能被采样到。

第1种情况: 直接把经过尺度伸缩后的一个离散子脉冲复制后乘以相应的权系数, 按照顺序排成顺次相连的一个向量来合成该尺度值对应的副本信号。

第2种情况: 以子脉冲持续时间结束点前的最后一个采样点作为这一子脉冲的结束点, 产生第1个离散子脉冲后乘上对应的权系数得到该尺度值对应副本信号的第1个向量; 以该结束点之后的第 1个采样点作为下一个子脉冲的开始点,产生第2个离散子脉冲后乘上对应的权系数得到该尺度值对应副本信号的第 2个向量, 直至第 2个子脉冲持续时间内能够采样到该时间段内的最后一个采样点; 再以该点之后的下一个采样点作为第3个子脉冲的开始点, 产生第3个离散子脉冲后乘上相应的权系数得到该尺度值对应副本信号的第3个向量, 依次周而复始直至得到该尺度值对应副本信号的最后一个向量, 最后把这些向量顺序排成顺次相连的一个向量来合成尺度向量中一个尺度值对应的副本信号。

由于尺度伸缩导致信号时宽的伸缩, 所以这些不同尺度值对应副本信号是长度不一样的向量,以副本信号中最长的向量长度加上发射信号的向量长度作为基准长度 L, 对所有尺度值对应的副本信号补零后得到新的向量, 并形成一个副本矩阵, 最终采用步骤3)得到PTFM信号的模糊度函数。事实上, 信号的采样率确定后, 大多数情况是这样的: 经过尺度伸缩后的子脉冲持续时间结束点不能被采样到, 即满足第2种情况。

下面根据上述方法合成 PTFM 的副本信号,以计算机仿真实现其模糊度函数, 并做出分析。选取信号参数如第 1节所示, 采样率是 16 kHz,尺度从0.96到1.04共81个副本, 例如当尺度为0.98时, 一个子脉冲的持续时间变成0.02/0.98 =0.020408, 而采样时间间隔为采样率分之一, 即为1/16 000=0.000 062 5, 0.020 408/0.000 062 5=326.528不是一个整数, 说明经过尺度伸缩后的一个子脉冲的持续时间结束点不能刚好被采到, 而下一个子脉冲开始点还是0.020 408时就会造成副本向量中信息移位和缺失。事实上只有尺度为 1处的子脉冲持续时间结束点刚好被采样到, 其余80个副本的合成都属于第2种情况。

图4为本文方法合成信号产生的模糊度函数图, 从图 4(a)可看出, 主峰和每一个旁峰呈图钉状, 从图 4(b)可看出, 时延-尺度面上分布的主峰和旁峰关于中心点处扭对称; 取出主峰分别沿时延、尺度轴做投影如图 4(c)和图 4(d)所示, 可以看出, 在时延轴上的投影和尺度轴上的投影都有一个尖峰。显然这些图都满足脉冲串信号模糊度函数的特点。

如果把所有的副本合成考虑成第 1种情况,直接复制、乘上相应的权系数后合成副本信号,那么将会导致大多数副本中向量信息的移位和信息的缺失, 最终导致模糊度函数出现错误。图 5即为错误的模糊度函数图。

从图 5可以看出, 虽然模糊度函数呈现钉板状, 但是其在时延-尺度面上的分布已经不呈现扭对称状了, 主峰在时延轴上的投影关于中心点处不对称, 在尺度轴上的投影不仅关于中心点处不对称, 而且没有形成 1个尖峰, 所有这些都不符合脉冲串信号模糊度函数的特点。显然, 错误的模糊度函数实现方法会对波形设计造成很大的影响。本文采用的基于FFT的频域快速处理方法,对于每个尺度值来说, 需要2次L点FFT运算、一次L点IFFT运算以及L/2次复数共轭乘法运算。每个FFT运算需要 L × log2L次乘法运算和加法运算。快速算法的乘法和加法运算的总数为3 L × log2L+ 3L /2, 与直接计算所需的L2次乘法和加法运算相比, 运算量显著降低, 极大地提高了运算效率。目前包括通用数字信号处理(digital signal processing, DSP)芯片在内的多数设备都具有针对FFT运算的专用硬件结构, 能满足宽带系统的实时性要求, 提高了数据处理能力。

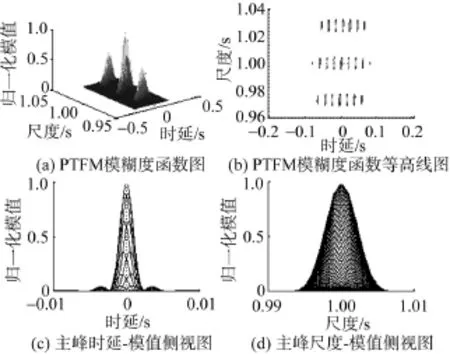
图4 本文方法合成信号产生的模糊度函数图Fig. 4 Ambiguity function diagram of the signal synthesized by the proposed method

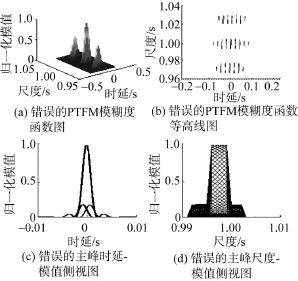
图5 错误的模糊度函数图Fig. 5 Wrong ambiguity function diagram

3 结束语

本文以 PTFM 信号的模糊度函数实现为例,研究了宽带脉冲串信号模糊度函数实现的过程,提出了对整个脉冲串信号进行尺度压缩后再重采样得到副本信号的方法, 合成副本信号采用基于FFT的快速处理方法仿真实现PTFM信号的模糊度函数, 该方法产生模糊度函数对信号分析、波形设计以及检测估计具有重要参考价值, 并且由于PTFM信号既是时间分集信号又是频率分集信号, 使得本文提出的合成副本信号而产生模糊度函数的方法对所有类型的脉冲串调频信号的模糊度函数实现具有通用性。

[1] Doisy Y, Deruaz L, Ijsselmuide S V, et al. Reverberation Suppression Using Wideband Doppler-Sensitive Pulses[J]. IEEE Journal of Oceanic Engineering, 2008, 33(4): 419-433.

[2] 王沛. 调频脉冲串宽带信号技术研究[D]. 北京: 中国科学院电子学研究所, 2005.

[3] Mayazzurra R, Genderen P V. Wideband Ambiguity Function and Optimized Coded Radar Signals[C]//Proceedings of the 4th European Radar Conference. Munich, Germany, 2007: 142-145.

[4] Xue J, Zeng W J, Li X L. Time Delay and Doppler Estimation for Wideband Acoustic Signals in Multipath Environments[J]. Journal of the Acoustical Society of America, 2011, 130(2): 850-857.

[5] 石勇, 蒋兴舟, 张静远, 等. 宽带模糊函数与窄带模糊函数表示的差异分析[C]//图像仿真信息技术. 第二届联合学术会议论文集, 北京: 2002.

[6] 李志舜. 鱼雷自导信号与信息处理[M]. 西安: 西北工业大学出版社, 2004: 138.

[7] 刘朝晖, 杨长生, 赵申东, 等. 水下声信号处理技术[M]. 北京: 国防工业出版社, 2010.

(责任编辑: 杨力军)

A Realization Method for Ambiguity Function of Wideband Pulse Train Signal

YUE Lei, LIANG Hong, YANG Chang-sheng
(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

The ambiguity function of wideband pulse train signal is a powerful tool for signal analyzing and waveform designing, and a common method in detection and estimation. Realization of the ambiguity function firstly needs synthesizing replicas. However, directly copying scale extension of the sub pulse and multiplying different weights to synthesize replicas may cause most replicas vectors losing and information missing. In order to solve this problem, this paper adopts a new method for synthesizing replica signal, in which the entire pulse train is firstly compressed and then resampled. Simulation on the pulse train of linear frequency-modulated waveforms′ ambiguity function shows that the method is feasible and applicable to achieve ambiguity function of wideband pulse train signal.

pulse train signal; ambiguity function; replica; resampling

TJ630.34

A

1673-1948(2014)02-0096-04

2013-07-22;

2013-12-02.

国家自然科学基金(61201322), (61379007).

岳 雷(1988-), 男, 在读硕士, 研究方向为信号与信息处理.