伺服阀用超磁致伸缩驱动器的相变温控研究
2014-06-04李兵华曹树平罗小辉
李兵华,曹树平,罗小辉
(华中科技大学机械科学与工程学院,湖北武汉 430074)
超磁致伸缩材料是自20世纪70年代迅速发展起来的新型功能材料,其尺寸伸缩可随外加磁场成比例变化,其磁致伸缩系数远大于传统的磁致伸缩材料,具有应变大、响应速度快、能量传输密度高和输出力大等优点[1]。经实验测试,采用GMM的驱动器控制精度小于 0.1 μm,频宽大于 1 000 Hz[2]。
GMM线性特性相对比较差,尤其受温度影响比较显著。实验研究:温度每升高1℃产生的热应变引起的输出微位移误差约为最大应变的 10-3[3]。而GMM一般通过导电线圈产生磁场实现伸长,其磁滞和涡流损耗以及导电线圈都会产生热量,所以必须采取有效的措施对GMM温度进行控制。文中采用了相变温控的方法,它是吸收型被动温控,不靠温差散热,也不受外界环境温度的制约,并能使受控对象始终稳定在需要的温度上;同时,相变温控装置体积小、质量轻、不耗电、没有运动部件,且无复杂控制系统[4]。
相变材料是指在相变过程中能吸收或释放潜热,且其温度维持不变的材料。如图1所示为给相变材料一个热源、相变材料随温度变化情况。刚开始相变材料处于固态,随着时间的延续,相变材料的温度开始上升;当温度上升到相变材料的熔点时,温度维持恒定状态,此时固态和液态的相变材料共存;继续给相变材料提供热量,直至完全融化,此时温度才继续上升;当停止给相变材料加热时,相变材料开始凝固,此时温度维持恒定,直至相变材料完全变成固体,温度才开始下降至室温。

图1 相变材料随温度的变化
1 GMA的总体结构及工作原理
如图2所示为GMA的总体结构图。预压螺帽1与导向固定环4通过螺纹进行连接,输出杆3传递GMM棒产生的位移,旋转预压螺帽1可以通过输出杆3和碟簧2向GMM棒施加预压力。导向固定环4用于顶住线圈骨架8,同时对输出杆3有导向作用,并通过螺钉与外壳11连接。元件5为导磁环,增加通过GMM棒的磁通量。驱动线圈9的骨架由绝热材料制成,固定驱动线圈9和偏置线圈10。驱动线圈9通电流产生磁场驱动GMM棒伸长;偏置线圈10产生偏置磁场,使GMM棒工作在线性区。相变材料12用于吸收线圈及GMM棒产生的热量,从而使GMM棒的温度保持恒定,支撑架13用于填充固定相变材料。

图2 GMA的总体结构图
为了保持GMM棒的温度恒定,可以在相变材料内布置加热电阻丝14,开始工作时,将相变材料加热到熔点温度。然后接通偏置线圈,持续为相变材料供热,使其温度恒定。GMM棒上布置温度传感器7,当GMM棒的温度高于相变材料的熔点时,使偏置线圈断电,只有当驱动线圈通电或相变材料温度低于熔点温度时才通电。
2 GMA的热数学模型
2.1 热分析的理论基础
热分析分为稳态传热和瞬态传热两种方式,文中主要采用的是瞬态传热。瞬态传热过程是指一个系统的加热或冷却过程,在这个过程中系统的温度、热流率、热边界条件以及系统内能随时间都有明显变化。根据能量守恒原理,瞬态热平衡可以表达为 (以矩阵形式表示):

其中:K为传热矩阵,包括导热系数、对流系数、辐射率和形状系数;T为节点温度向量;Q为节点热流率向量,包括热生成;C为比热矩阵,需要考虑系统内能的增加;为温度对时间的导数。
非稳态的温度分布取决于导热热阻和对流热阻的比值,可用一特征数来表示这一比值。所谓特征数,它是表征某一类物理现象或物理过程特征的量纲为一的数,又称准则数。毕渥 (Biot)数用Bi表示,定义为导热热阻与对流热阻的比值,即:

式中:δ为特征长度,γ为平壁的导热系数,h为平壁的表面传热系数。
(1)当Bi很小时,即传热热阻主要是边界对流热阻,因而平壁表面和流体存在明显的温差。这一温度随着时间的推移和平壁总体温度的降低而逐渐减小,由于这时导热热阻很小,可以忽略不计,故同一时刻平壁的温度可近似认为是相同的,此时可用集总参数法即忽略物体内部导热热阻的简化方法,把质量和热容量汇聚到一点,只需求出温度随时间的变化规律,以及在温度变化过程中物体放出或吸收的热量。由集总参数法求出的物体温度随时间的变化关系为:
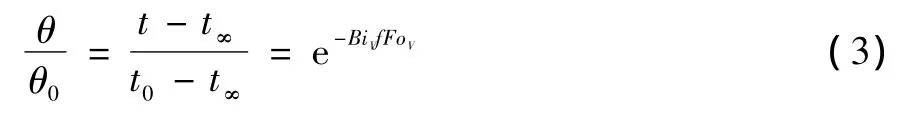
式中:θ0为过余温度;t0为平壁初始时刻温度;t∞为外界温度;BiV为内外热阻之比;FoV为傅里叶数,由定义:

式中:τ是计算时刻为止所用的时间,a是扩散系数,分母可视为热扰动扩散到l2面积上所需的时间。FoV越大,热扰动就越深入地传播到物体内部,物体的温度就越接近周围介质的温度。物体温度随时间的变化规律确定之后,就可以知道物体和周围环境之间从τ=0到τ时刻所传递的总热量为:

式中:ρ为材料密度,c为比热容,V为体积。
(2)当毕渥数不满足集总参数法的条件,即BiV<0.1M时,就必须考虑物体的几何形状和大小,不能再将物体集总为一点,这时分析求解是比较困难的,只有当几何形状及边界条件都比较简单时才可获得分析解。文中所分析的模型为圆柱模型,经过分析,对于一维圆柱在第三类边界条件下的非稳态导热问题 (即给出了边界上物体表面与周围流体间的表面传热系数及流体的温度),可以导出和平壁形式类似的温度分布,即
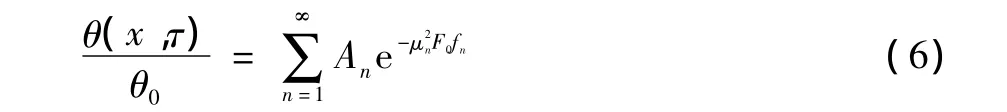
2.2 GMA的热量来源
GMA实际工作中的热量来源主要有3个部分:驱动线圈产生的热量Q1,偏置线圈产生的热量Q2,GMM棒的涡流和磁滞损耗,则GMA产生的总热量为:

而这里所设计的GMA实际工作中驱动线圈和偏置线圈都通直流电,所以GMM棒内无涡流产生,而磁滞损耗相比线圈产生的热量极小,可以忽略不计。则这时GMA产生的总热量为:

2.3 所填充的相变材料总的潜热
相变材料的潜热计算公式为:

式中:V为所填充的相变材料体积,ρ为单位体积潜热。实验中选用氨腈 (HNCNH),其熔点温度为44℃,单位体积潜热ρ为1.08×109J/m3。
填充的相变材料体积V为:

式中:d1为填充的相变材料外径20 mm,d2为内径9 mm,h为支撑架长度94 mm,代入式 (10)可得V为2.354×10-5m3。则相变材料的潜热:

3 GMA的热特性仿真研究
GMA相关参数的具体值见表1。

表1 GMA相关参数的具体值
利用ANSYS进行瞬态热分析包括4个基本步骤:(1)建立有限元模型;(2)施加载荷计算;(3)求解;(4)后处理。
文中进行热分析的目的就是要看给线圈加恒定电流后,靠近GMM棒的相变材料不同位置随时间的变化。为了进行对比分析,首先仿真研究了没加相变材料时的GMA温度特性。建立GMA截面几何模型如图3所示。几何模型建好后通过划分网格加载求解3 h后GMA的温度分布如图4所示,可见温度分布并不均衡。为进一步分析其特性,选取靠近GMM棒的A、B、C、D、E5个点,这5个点的温度随时间的变化情况如图5所示。可以看出:温度变化最大的点为点A,为10.25℃;温度变化最小的点为点E,为9.75℃,两点的温差为0.5℃。

图3 GMA几何模型

图4 3 h后GMA温度分布
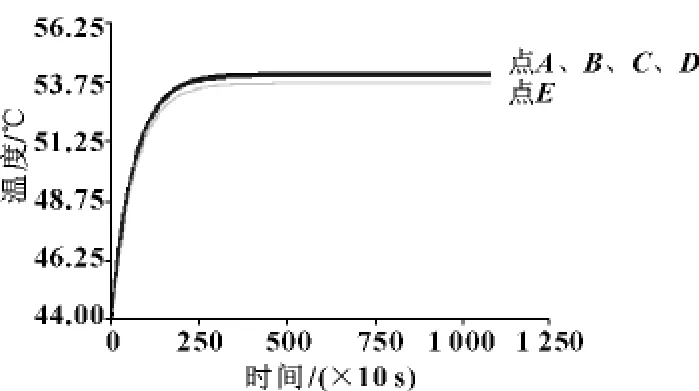
图5 靠近GMM棒的5点温度分布图
图6所示是加了相变材料的GMA的截面简化几何模型。图7所示是在30 h后GMA截面的温度分布图,可以看出:靠近GMM棒的部分温度分布比较均匀。
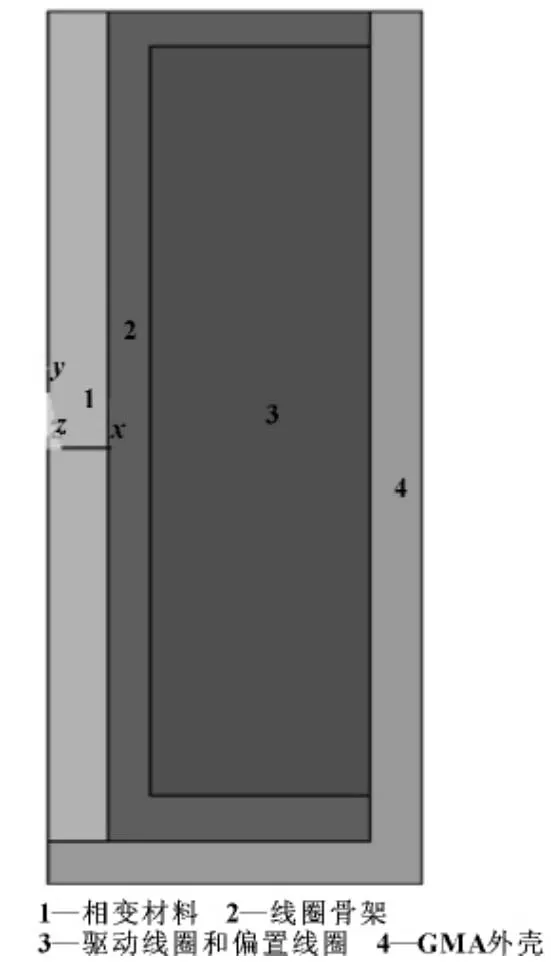
图6 GMA载面几何模型

图730 h后GMA 热分布
为了进一步分析线圈产生的电流对GMM棒温度的影响情况,取靠近GMM棒的相变材料上的A、B、C、D、E5个点,这5个点的温度随着时间的变化情况如图8所示:其中温度变化最大的是点B,为0.75℃;温度变化最小的是点E,为0.3℃。随着时间的延迟,这5个点的温度都趋于恒定,温度恒定后,温差最大的是点B和点E,为0.45℃。
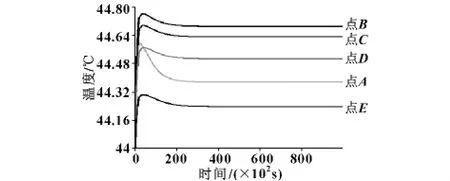
图8 相变材料各点温度随时间的变化曲线
通过以上的仿真对比可知:加相变材料后,能将GMM的温度变化维持在0.75℃以内;而不加相变材料,GMM棒的温度变化超过10℃。所以加入相变材料后,GMM棒的温度得到了很好的控制,从而大大提高了GMA的输出位移随驱动磁场变化的精确度。
4 结束语
对GMA的相变温控补偿进行了研究,分析了热量的来源,计算了所填充的相变材料的潜热,建立了GMA的截面几何模型,对其进行了瞬态热分析,并选取了相变材料上靠近GMM棒的5个点,分析了这5个点温度随时间的变化。通过仿真对比分析可知:加入相变材料后GMM棒的温度得到了很好的控制,GMA的输出精度得到了很大的提高。
[1]王传礼,丁凡,张凯军.基于超磁致伸缩转换器的流体控制阀及其技术[J].农业机械学报,2003(5):164-167.
[2]王传礼.基于GMM转换器喷嘴挡板伺服阀的研究[D].杭州:浙江大学,1998.
[3]LIU Dezhong,FEI Renguan,LI Jianfeng,et al.Development of Magnetostrictive Micro-actuator[J].Journal of Beijing Polytechnic University,2002(4).
[4]WU Y,XU J.Research on Methods of Thermal Error Compensating and Restraining in Giant Magnetostrictive Actuator[J].Journal of Engineering Design,2005(4):4.
[5]LIU Chuhui.Application of Phase Change Temperature Control to GMA[J].Modular Machine Tool& Automatic Manufacturing Technique,2006(10):16.
[6]贾振元,杨兴,郭东明,等.超磁致伸缩材料微位移执行器的设计理论及方法[J].机械工程学报,2001,37(11):46-49.
[7]邬田华.工程传热学[M].武汉:华中科技大学出版社,2011.
[8]邬义杰,刘楚辉.超磁致伸缩驱动器设计方法的研究[J].浙江大学学报:工学版,2004,38(6):747-750.
