基于三维测量的圆度误差执行不确定度研究
2014-06-04黄美发肖萌萌孙永厚陈磊磊
黄美发,肖萌萌,孙永厚,陈磊磊
(桂林电子科技大学机电工程学院,广西桂林 541004)
测量不确定度是评价测量结果质量的重要指标,测量不确定度定义为:表征合理地赋予被测量值的分散性,与测量结果相联系的参数。没有不确定度的测量结果是不完整的[1]。测量不确定度又可分为方法不确定度和执行不确定度。测量不确定度约定规则使不同国家、不同地区、不同学科和不同领域,在表示测量结果及其不确定度时具有一致的含义。
三坐标测量机在应用中,引起被测参数不确定度的来源非常复杂,它不仅与测量机本身的精度有关,还与采样策略、被测工件、环境条件及数据处理方法等一系列因素有关[1]。文中讨论的测量不确定度是在特定的采样、评定方法下评定的,属于测量不确定度中的执行不确定度。执行不确定度是实际认证操作算子定义的计量特性与理想认证操作算子定义的理想计量特性之间差异引起的不确定度,校准的目的通常是评估由测量仪器引起的执行不确定度的值,而与测量仪器没有直接关系的因素 (如环境)也可能导致执行不确定度[2]。文中根据最新国际标准 JCGM 101-2008,探讨利用坐标测量机进行圆度测量的不确定度的来源及评定方法;然后,根据我国计量技术规范JJF 1059.2-2011,运用自适应蒙特卡洛方法对圆度误差的评定过程进行仿真研究,从而验证了GUM的有效性,并给出了其适用的范围。
1 圆度误差评定模型[3]
圆度误差是指在垂直于回转体轴线截面上,实际轮廓对其理想圆的变动量,误差的大小直接关系到孔轴配合的精度。圆度误差是评价回转类零件形状精度的重要指标之一[4]。设回转体的测量工作平面为xy,轴线方向为z方向,Pi(xi,yi)为回转体某固定截面上的N个测量点在工作平面上的投影坐标,理想圆的方程为:
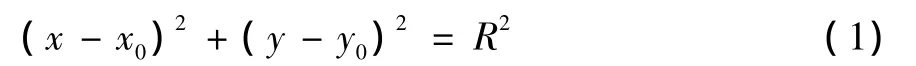
拟合的最终目的是确定理想圆的圆心坐标 (x0,y0)和半径R。目标函数为
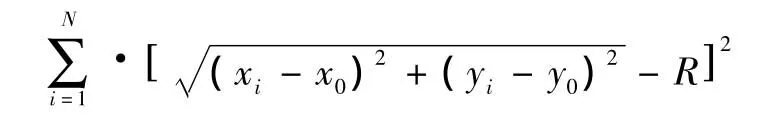
该表达式比较复杂,为非线性优化模型,对它进行线性化,整理公式 (1)得:


其中:x0,y0,C为未知量,根据极值条件,可以确定目标函数里的决策未知量。通过求解,可以得到:
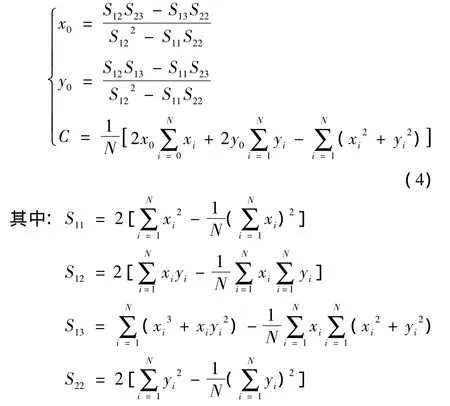

该公式推导的前提是圆心坐标(x0,y0)的绝对值足够小,只有圆心坐标足够小时才能作线性变换。因此,每次求解后,需要以求得的圆心坐标为坐标原点,对测量数据进行平移,然后再进行下一次的迭代,直到求得的圆心坐标绝对值足够小。
求得圆心坐标后,进而可以确定距离圆心最远和最近的测点,设两者分别为(x1,y1)、(x2,y2)。因此圆度误差模型为:
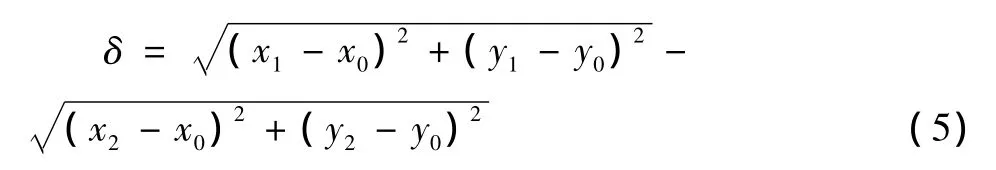
2 基于GUM圆度执行不确定度的评定
在三坐标测量机的测量过程中,存在多种测量因素对测量结果带来影响,主要包括:(1)测量重复性误差;(2)机构误差;(3)力变形误差;(4)热变形误差;(5)探测系统误差;(6)动态测量误差[1,3]。
其中,机构误差包括定位误差 (阿贝误差和标尺读数系统的误差)、角运动误差和直线度运动误差。测量重复性误差和机构误差直接影响测量点的坐标值,其他误差来源则对最终测量结果产生影响[1]。
圆度误差测量模型可表示为[5]:
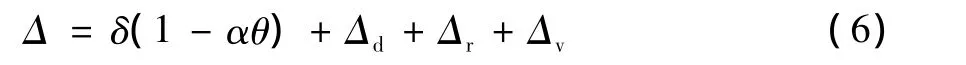
式中:δ为测量重复性误差和机构误差产生的误差,也是式 (5)中的评定误差;α为工件的热膨胀系数;θ为实际环境温度与标准测量环境温度之差;Δd为测量机的探测误差;Δr为测量机的力变形误差;Δv为测量机的动态误差。
各传递系数为:
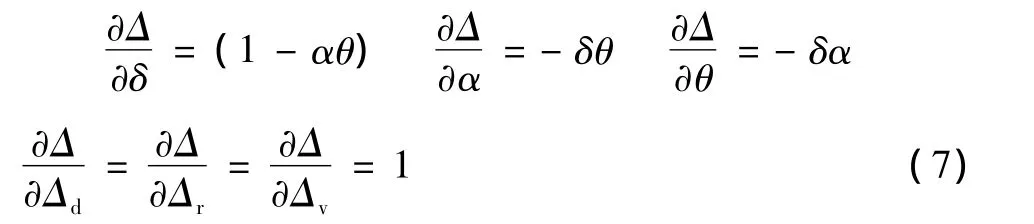
而圆度测量的执行不确定度为各个分量不确定度的平方和开方,即:
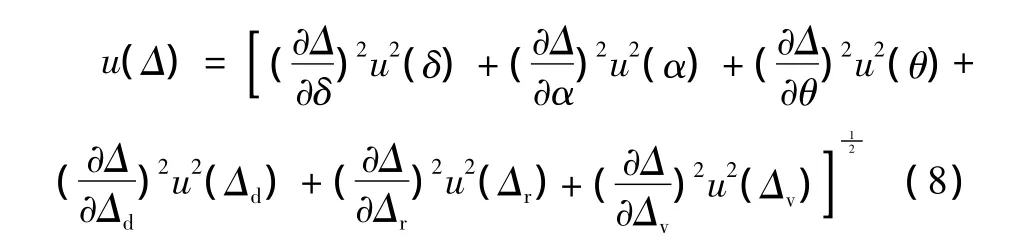
其中由测量重复性误差和机构误差引起的不确定度,可以通过式 (5)推导出。根据GUM不确定度传播规律,求得各传递系数为:
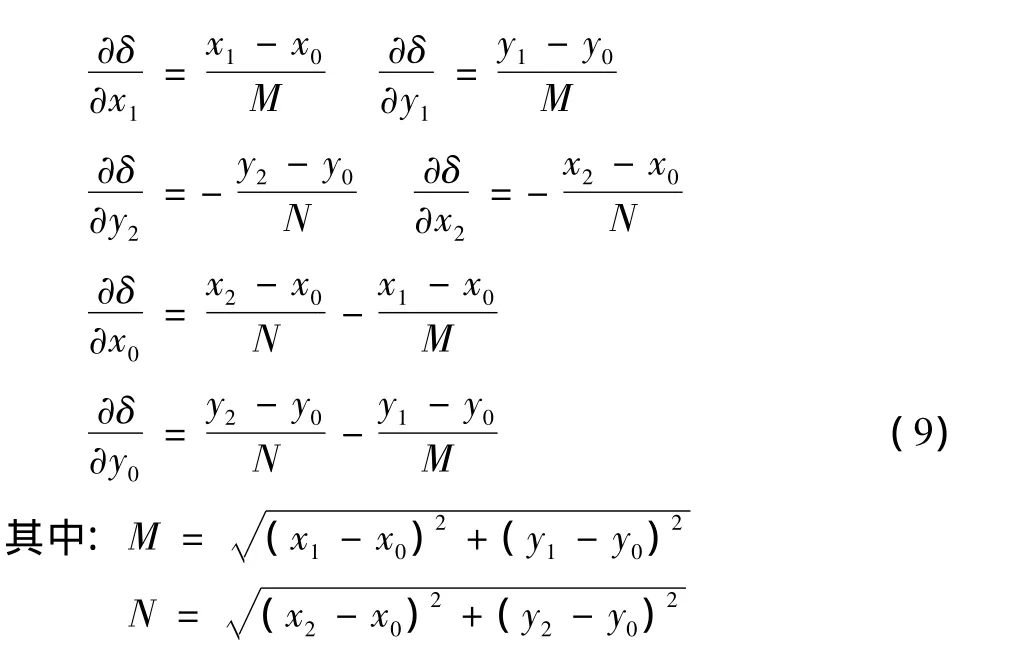
在所有的影响因素中,近似认为只有x0、y0是相关的。因此,可得由测量重复性误差和机构误差引起的不确定度[6]:
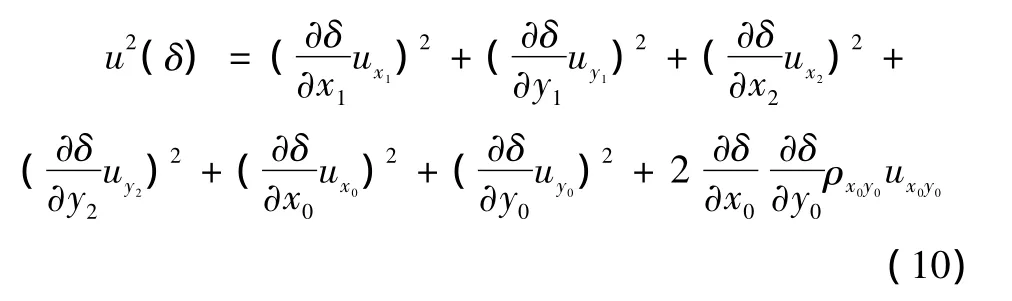
为保守考虑,取 ρx0y0=1。以上公式中x1、y1、x2、y2的不确定度由重复性测量和三坐标测量机的机构误差构成:
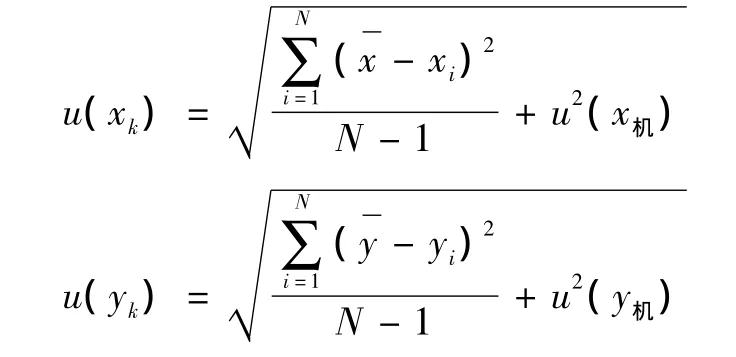
其中:k=1,2,…,N;u2(x机)为x轴方向上的机构误差不确定度;u2(y机)为y轴方向上的机构误差不确定度。
把(x0,y0)看作一个随机向量,对被测圆按照相同的采样方法拟合多次,计算随机向量的均值(,),作为它们的估计值代入式(9)。x0、y0的不确定度及相关不确定度为:
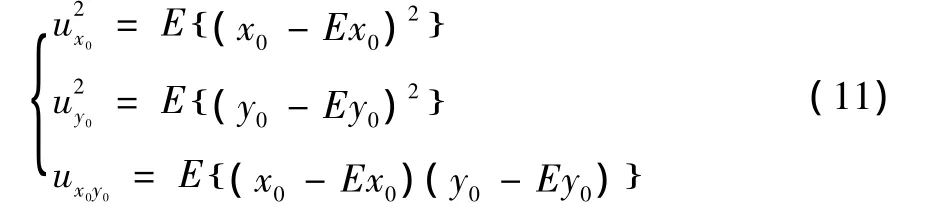
3 自适应蒙特卡洛方法 (MCM)
蒙特卡洛方法是一种数值计算方法,它以概率统计为主要理论基础,以随机抽样为主要手段。蒙特卡洛方法首先建立一个与所求解相关的概率模型,使所求问题的解正好是所建模型的数学期望或其他有关特征量;然后通过多次模拟一个统计试验,统计出某事件发生的概率;利用建立的概率模型,求出要估计的参数;最后对模拟结果进行分析总结,验证该系统的某些特性[7-8]。
在执行自适应蒙特卡洛方法的基本过程中,蒙特卡洛试验次数不断增加,直至所需要的各种结果达到统计意义上的稳定。如果某结果的两倍标准偏差小于标准不确定度的数值容差时,则认定该数值结果稳定。具体的评定步骤如下:
(1)分析圆度测量中执行不确定度的来源Δd、Δr、Δv、xk、yk、α,并确定其分布类型、分布区间、期望值及标准方差;
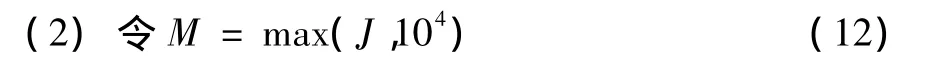
式中:J是大于或等于1/(1-p)的最小整数,p为包含概率,设h=1,表示在序列中初次应用MCM。
(3)执行M次蒙特卡洛实验:根据步骤 (1)确定的期望值和标准方差,生成M组随机数,以此模拟生成的触测点的坐标;
(4)代入圆度误差不确定度评定模型式 (6),计算得 到M个 模 型 值 Δ1,…,ΔM,并 统 计 Δ(h),u(Δ(h)),和,它们分别为圆度误差Δ的估计值、标准不确定度、100p%最短包含区间的左右端点;
(5)如果h=1,h增加1,返回到步骤 (3);
句中“公族疏远者”, “疏远”修饰“公族”,“者”为标志。句意:(吴起) 刚到楚国楚王就任命他为国相。他使法令明确,依法办事,令出必行,淘汰并裁减无关紧要的冗员,停止疏远的王族的按例供给,来供养战士。
(6)按下式计算圆度误差Δ的估计值Δ(1),…,Δ(h)的平均值的标准偏差SΔ
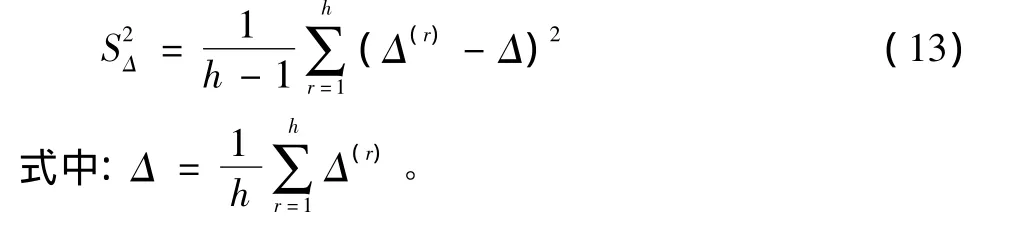
(7)以相同的方式分别计算u(Δ(1)),…,u(Δ(h))的平均值的标准偏Su(Δ),,…,的平均值的标准偏差SΔlow以及,…,的平均值的标准偏差SΔhigh;
(8)利用所有的h×M个模型值来获得u(Δ);
(9)设定不确定度的有效数字的位数,计算出数值容差σ(不确定度最短区间的半宽度);
(10)如果 2SΔ、2Su(Δ)、2SΔlow、2SΔhigh中的任何一个值大于δ,则h增加1并返回到步骤 (3);
(11)若所有的计算已达稳定,利用获得的h×M个模型值计算出Δ、u(Δ)和100p%包含区间。
4 实例分析
运用海克斯康三坐标测量机 (GLOBAL CLASSIC SR07.10.07),在φ151 mm的圆周上均匀测量20个点,评定圆度误差及其不确定度。通过查询该三坐标的技术参数可知,α=1.8×10-5℃-1,u(α)=0.05×10-5℃-1,θ=1 ℃,u(Δd)=0.2 μm,u(Δr)=0.2 μm,u(Δv)=0.2 μm,u(xk)=u(yk)=0.5 μm,不考虑温度的不确定度,各个随机变量符合正态分布,分别运用两种方法评定测量执行不确定度。最后假设各个随机变量符合均匀分布,再重新确定其执行不确定度。要求包含概率为95%,不确定度保留1位有效数字。
4.1 随机变量符合正态分布
GUM。根据20个离散点计算圆心坐标x0、y0,通过仿真模拟的方法,运用概率统计的相关知识计算估计值、不确定度以及相关不确定度;然后通过拟合算法,求得峰点坐标(x1,y1)、(x2,y2);然后根据式(7)、式 (9)计算各种误差源的传递系数;最后将计算结果代入式 (6)得到执行不确定度。
自适应MCM。运用第3节的评定步骤,评价出圆度误差及其执行不确定度。
由于不确定度保留1位有效数字,所以数值容差为σ=0.5 μm。两种方法得到的结果如图1、表1所示。

图1 圆度误差概率分布对比

表1 各种评定方法计算结果比较
结果分析:
(1)由图1可知:各个误差源符合正态分布时,最后的圆度误差的概率分布比较接近正态分布,仅仅圆度误差估计值与标准不确定度存在偏差;
(2)由表1可知:自适应MCM和MCM运算结果十分接近,可见100 000次与50 000次的仿真结果十分接近,且在数值容差范围之内,说明自适应MCM的计算结果是可信的,提高了计算效率;
(3)由表1比较MCM和GUM的计算结果,圆度误差相差0.1 μm,不确定度相差0.2 μm,包含区间左右端点均相差0.4 μm,圆心坐标与半径相差在0.1 μm以内,各项计算结果都小于数值容差σ,说明GUM在微米级精度范围内是有效的。
4.2 随机变量符合均匀分布
运用相似的方法,对执行不确定度重新评定,结果如图2、表2所示。
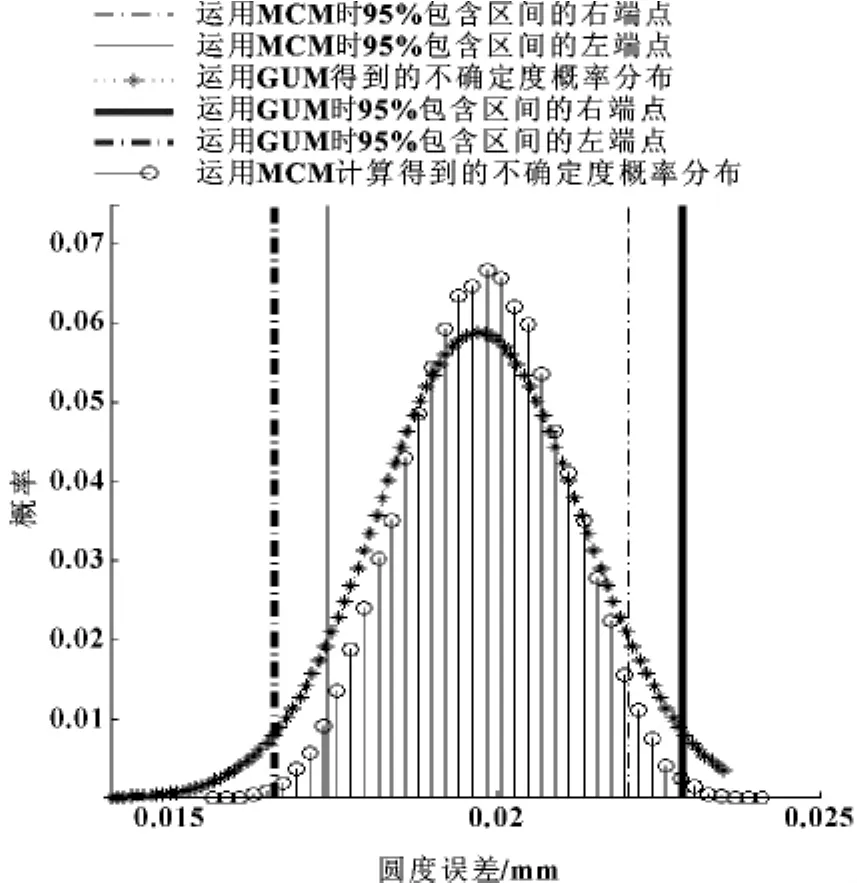
图2 圆度误差概率分布对比

表2 两种评定方法的比较
结果分析:
(1)由图2可知:各个误差源符合均匀分布时,最后的圆度误差的概率分布偏离正态分布较大;
(2)由表2可知:在误差源符合均匀分布时,自适应MCM和MCM运算结果偏差在数值容差范围之内,说明自适应MCM的计算结果是可信的,证明了自适应MCM的有效性;
(3)由表2比较MCM和GUM的计算结果,不确定度相差0.4 μm,包含区间左右端点分别相差0.8 μm、0.9 μm,超出了数值容差,说明在该情况下GUM在微米级精度范围内是无效的。
4.3 测点数量对不确定评定的影响
从评定模型的推广角度考虑,分析了测量点数对不确定度的影响。运用上面介绍的方法,在误差源符合正态分布的情况下,分别测量8、10、12、14个点,并对不确定度进行重新评定,结果如图3所示。
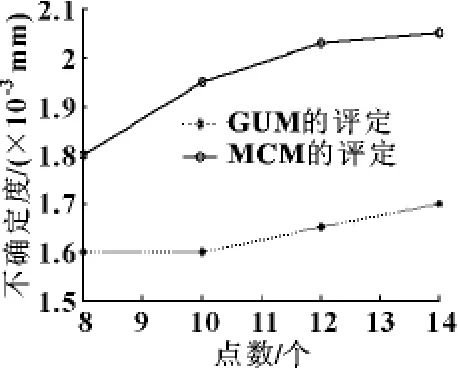
图3 测量点数对不确定度评定的影响
结果分析:
(1)随着测点的增加,MCM得到的执行不确定度也会增大,增长的速度会变慢,但测量点数对GUM的评定结果影响不大。
(2)在正态分布的条件下,两种评价结果的最大偏差在数值容差范围内,说明在微米级的精度范围内GUM是可信的。
4.4 实验结论
(1)基于GUM的不确定度评定,采用了近似的处理。未考虑峰点与拟合后的特征参数的相关不确定度,比如圆的提取点与圆心认为是不相关的;测量点数对执行不确定度的影响未体现出来,除峰点以外的提取点对合成不确定度的影响未考虑。因此GUM计算的精度降低。
(2)研究表明,测点坐标误差不确定度和圆度误差合成不确定度的概率密度函数较大程度地偏离正态分布或t分布,特别是分布明显不对称时,不适合用GUM来评估不确定度。相反,在允许的精度范围内,由于GUM运算规模小,推荐使用GUM评定。
5 结束语
综合考虑了三坐标测量机进行形状误差测量时自身误差和测量过程中引入的各项误差,给出了基于测量不确定度表示指南 (GUM)估算执行不确定度的方法,并利用自适应蒙特卡洛仿真方法 (MCM)来验证GUM方法的有效性及其适用范围。GUM通过严格的理论推导,计算规模小,但是不能适用所有的场合。实验结果表明:文中所提的不确定度评定模型,能有效提高三坐标测量结果的准确性和可信度。
[1]全国产品尺寸和几何技术规范标准化技术委员会.GB/T 24635.3-2009产品几何技术规范(GPS)坐标测量机(CMM)确定测量不确定度的技术:第3部分:应用已校准工件或标准件[S].北京:中国标准出版社,2009.
[2]蒋向前.新一代GPS标准理论与应用[M].北京:高等教育出版社,2007.
[3]张国雄.三坐标测量机[M].天津:天津大学出版社,1999.
[4]方沁林.圆度误差评定的算法研究与软件设计[D].武汉:华中科技大学,2007.
[5]JCGM 101:2008 Evaluation of Measurement Data-Supplement 1 to the"Guide to the Expression of Uncertainty in Measurement"——Propagation of Distributions Using a Monte Carlo Method[S].JCGM - WG1,2008.
[6]国际标准化组织.测量不确定度表示指南[M].刘智敏,刘增明,译.北京:标准化文摘杂志社出版,1995.
[7]陈晓怀,薄晓静,工宏涛.基于蒙特卡洛方法的测量不确定度合成[J].仪器仪表学报,2005,26(8):759 -761.
[8]黄美发,景晖,匡兵,等.基于拟蒙特卡洛方法的测量不确定度评定[J].仪器仪表学报,2009,30(1):120-124.
