基于切比雪夫多项式的新形式调频变标合成孔径雷达成像算法
2014-06-02侯育星陈士超冯大政邢孟道
侯育星 陈士超 唐 禹 冯大政 邢孟道
基于切比雪夫多项式的新形式调频变标合成孔径雷达成像算法
侯育星*陈士超 唐 禹 冯大政 邢孟道
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
该文提出一种基于切比雪夫(Chebyshev)多项式逼近的新形式的调频变标(Chirp Scaling, CS) SAR成像算法。该算法采用切比雪夫多项式逼近替代了原始CS算法中对回波信号2维频谱的泰勒(Taylor)级数展开近似,公式更加精确。然后利用光学系统抽象出的数学模型确定变标函数以校正距离徙动。并且该算法使由近似引入的误差有了上界限,改善了场景边缘点的聚焦效果,增加了场景的聚焦深度。仿真结果验证了该算法的有效性。
合成孔径雷达雷达成像;切比雪夫多项式;调频变标(Chirp Scaling)算法
1 引言
合成孔径雷达(SAR)具有全天候、全天时、远距离成像的特点[1],通过距离向的宽频带和平台运动形成的长线性合成阵列,分别实现了距离向和方位向的高分辨。频域SAR成像快速算法的实质为在信号频域实现距离向与方位向的2维分离,然后分别进行匹配滤波处理,最后变换到图像域得到2维的高分辨。但在实际情况中,由于SAR系统固有的特性,距离向与方位向存在耦合问题,使得匹配滤波不能完全实现匹配。因此在成像处理前必须对回波信号的相位进行2维解耦合处理。精确的2维频谱是设计频率域快速成像算法的前提[2],传统的频域SAR成像算法都以泰勒(Taylor)级数展开为基础,对信号的2维频谱进行不同程度的近似[3],进而进行相位因子补偿[4]。1994年文献[5]首次提出了调频变标(Chirp Scaling, CS)算法,CS算法通过对线性调频信号进行频率调制,实现不同距离单元上距离单元徙动(Range Cell Migration, RCM)差量的校正,使所有距离单元上的距离徙动曲线与参考距离处的距离徙动曲线一致,然后在2维频域进行统一补偿,避免了插值操作。因此CS算法被广泛地开发应用于机载星载[6,7]等不同的系统中和各种模式[8,9]的成像中。由于CS算法依靠Taylor级数对信号的精确2维频谱进行多项式展开,因此由2维频谱近似所产生的误差大小非常重要,将直接影响到算法的最终精确度。而由Taylor级数的数学模型的特性所决定的,在阶数一定的情况下,近似误差会随着远离展开点而单调增加,这就导致了当场景较宽时,传统CS算法在边缘点成像时由于误差增大而产生散焦,聚焦深度不够的情况,若采用分块处理[10],运算量又太大。针对这一情况,本文提出了一种基于切比雪夫(Chebyshev)多项式[11]的新形式CS算法,该数学模型比Taylor级数精确度高,而且具有有限误差界的性质,该性质很好地改善了场景边缘点的的聚焦效果,增加了场景的聚焦深度。文献[12]首先将其应用在双基地雷达系统中,利用切比雪夫多项式逼近瞬时斜距函数,并结合级数反演(Reversion of the Series Method, MSR)得到了双基SAR信号的2维频谱,取得了很好的效果。
本文提出了一种可以得到更高谱精度的基于切比雪夫多项式展开的新CS算法。文章首先对基于切比雪夫多项式逼近的信号2维频谱的表达式进行了推导,然后利用光学系统确定变标函数[13],实现脉冲压缩聚焦成像;此外,文中对该算法的误差进行了分析,并与传统CS算法进行了比对;最后通过仿真实验验证了算法的有效性。
2 算法原理
2.1 切比雪夫多项式


2.2 2维频谱


在式(2)中,第3个相位项为耦合项,即包含随距离单元空变的距离徙动项(RCM),在成像前需要进行解耦合处理才能正确补偿,现将这一项单独列出来:




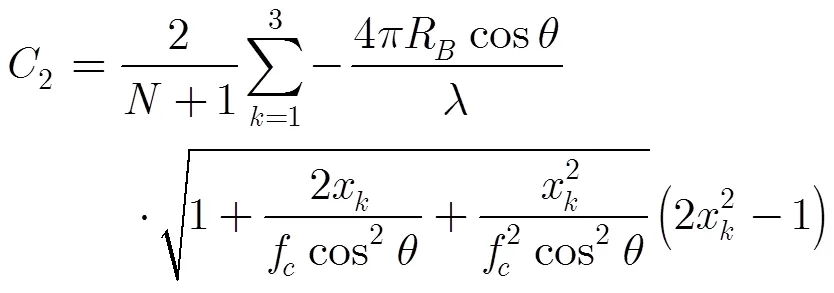

至此,本文已经将切比雪夫多项式逼近引入到了SAR信号回波公式中,求出了2维频谱的表达式。但是这种展开方法并没有消除信号的耦合现象,并没有解决掉所关心的距离徙动空变问题,不能直接进行2维补偿和脉冲压缩操作,因此接下来算法推导的关键在于利用变标操作统一距离徙动大小。
2.3 调频变标算法
利用驻相点原理,将式(6)直接进行距离向傅里叶逆变换,得到距离多普勒域信号

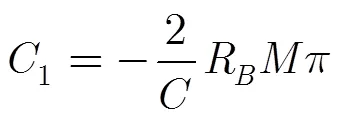

文献[15]将光学信号的数学模型抽象出来应用到了SAR成像算法中,本文将类比这一模型来确定变标函数。光学信号的模型框图经过一定的修改后,对应SAR成像的变标算法的框图如图1所示。
根据图1构造CS变标函数:
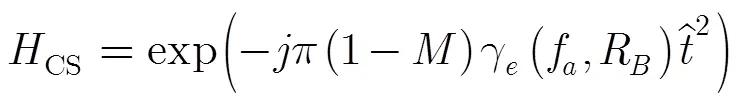
对于正侧视或小斜视情形,式(10)中随的变化较小,可将近似为,
为使表述简洁,只将式(7)的第3个相位项与变标函数相乘结果单独列出:

与变标函数相乘完成变标后,构造用于距离压缩的匹配滤波函数:

此时已经完成距离徙动校正及距离压缩。接下来进行方位向处理,补偿方位向相位和剩余相位。

最后将图像变到2维时域,得到了2维聚焦后的图像。
3 误差分析及实验仿真
为了验证本文所提算法的有效性,对算法进行了误差分析及仿真验证。仿真时采用模拟的正侧视机载参数,主要参数如表1所示。
3.1误差分析
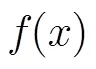
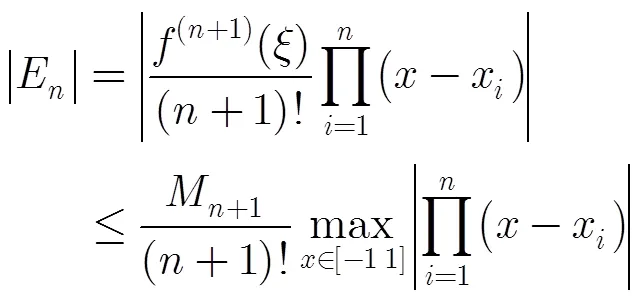
表1仿真主要参数

载频(GHz) 波长(m) 带宽(MHz) 脉冲重复频率(Hz) 场景中心距离(km) 方位向分辨率(m) 载机速度(m/s)
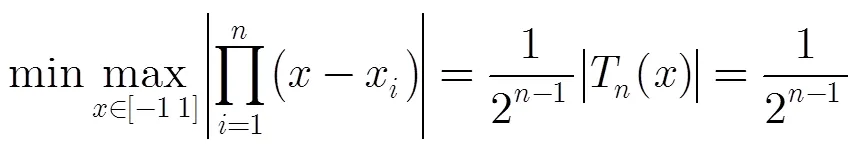

式(16)即为切比雪夫多项式逼近的误差上界。
3.2 点目标实验仿真

图2 两种近似的误差对比

图3 切比雪夫算法的距离徙动校正效果对比
场景中心点聚焦剖面图结果如图4所示。
10 km边缘点目标聚焦剖面图结果如图5所示。
由图4和图5可以明显看出,两种算法的中心点目标的聚焦效果均很好,但在边缘点的聚焦效果上,本文提出的算法明显优于传统的算法,验证了节3.1的误差分析中由切比雪夫多项式的性质得到的结果。最后通过计算点目标聚焦后的峰值旁瓣比(Peak to SideLobe Ratio, PSLR)和积分旁瓣比(Intergrated SideLobe Ratio, ISLR)来定量的分析聚焦效果。
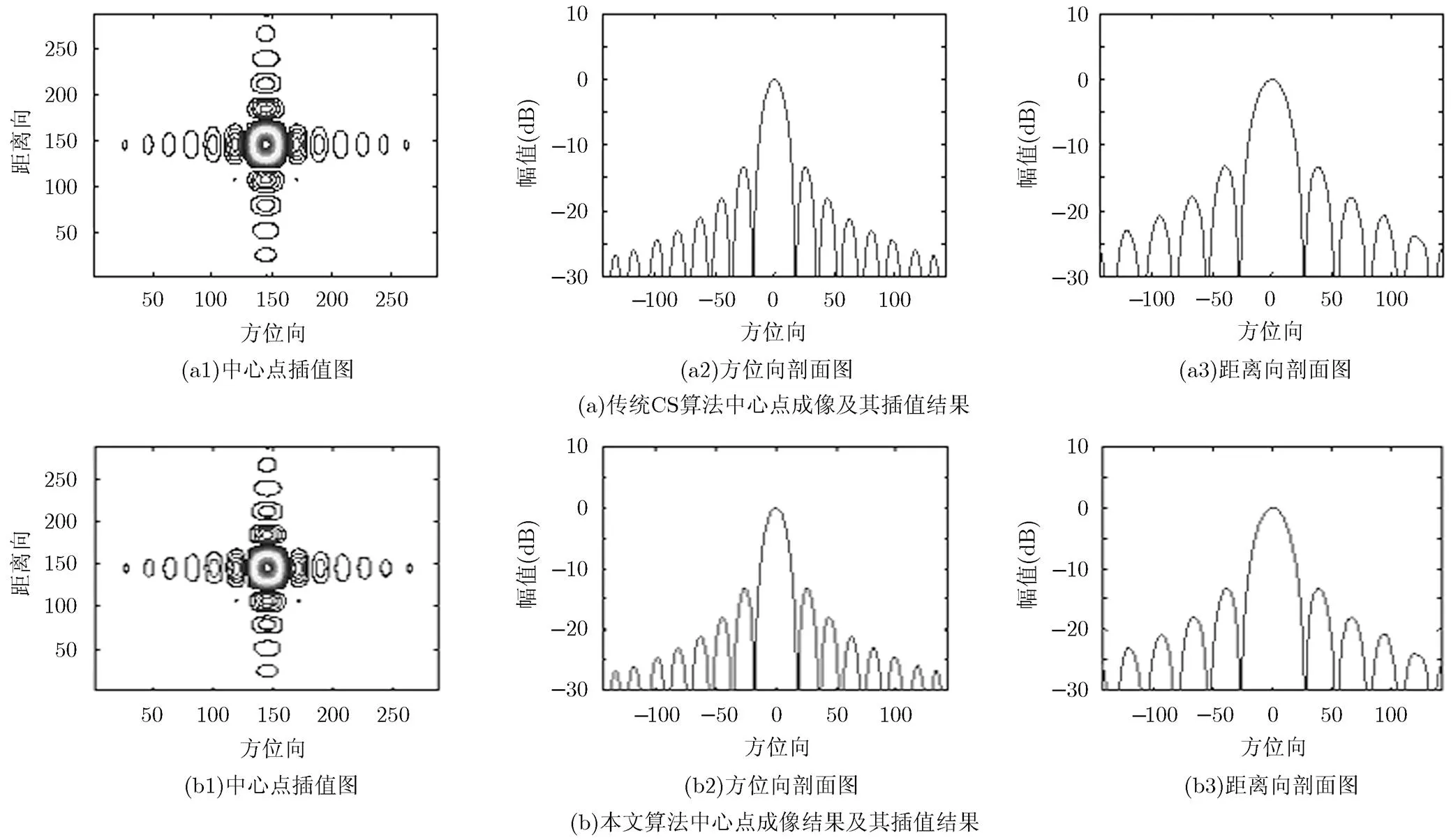
图4 两种算法场景中心点目标仿真图

图5 两种算法场景边缘点目标仿真图
表2本文方法与传统方法PSLR与ISLR结果对比(dB)
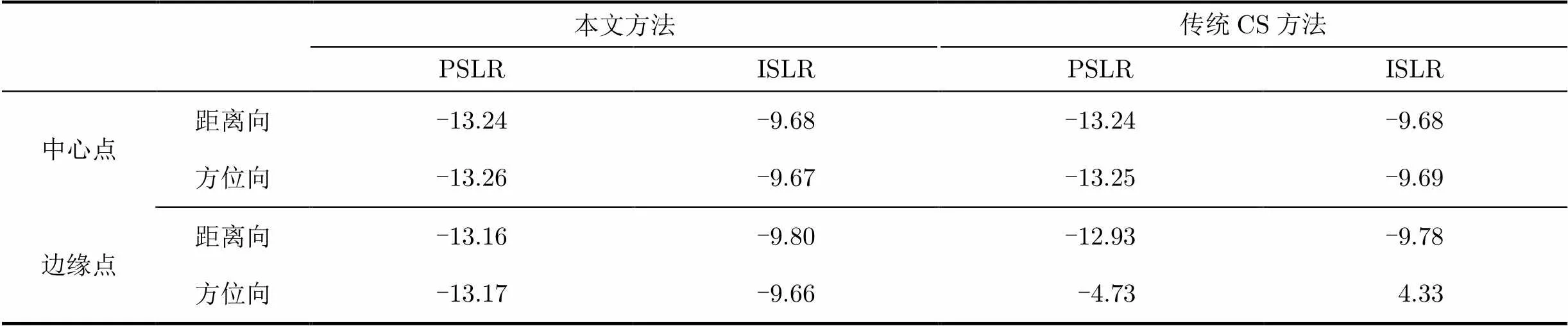
本文方法传统CS方法 PSLRISLRPSLRISLR 中心点距离向-13.24-9.68-13.24-9.68 方位向-13.26-9.67-13.25-9.69 边缘点距离向-13.16-9.80-12.93-9.78 方位向-13.17-9.66 -4.73 4.33
4 结束语
本文提出了一种基于切比雪夫多项式逼近的CS成像算法,使用一种新的数学近似模型代替了原来Taylor级数展开,将回波信号的2维谱进行了更精确的近似,并根据展开的公式重新确定了变标函数,实现了对距离徙动的补偿,很好地完成了场景聚焦成像。文章最后对新算法与传统算法的误差进行了分析对比,从分析结果可以看出新算法的优势:使近似产生的误差有了界限,不再随着远离展开点而增加,从而边缘点聚焦效果更好,增加了场景聚焦深度。取得了比较好的效果,最后的目标仿真结果进一步验证了本文的算法的有效性。本文基于理想模型下验证了切比雪夫多项式逼近和SAR算法结合的可行性,后续的工作将会进行实测数据的处理,进一步验证该算法的有效性。
[1] Sun Guang-cai, Xing Meng-dao, Liu Yan,.. Extended NCS based on method of series reversionfor imaging of highly squinted SAR[J]., 2011, 8(3): 446-450.
[2] 陈士超, 武其松, 刘明, 等. 严格解析谱下同航线双基SAR频率变标成像算法[J]. 电子与信息学报, 2011, 33(6): 1447-1452.
[3] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 151-165.
[4] 王亮, 王建, 黄晓涛, 等. Chirp Scaling 算法中相位补偿因子研究[J]. 电子与信息学报2007, 29(1): 6-11.
[5] Raney R K, Runge H, Bamler R,.. Precision SAR processing using chirp scaling[J]., 1994, 32(4): 786-799.
[6] 李春升, 杨威, 王鹏波. 星载SAR成像处理算法综述[J]. 雷达学报, 2013, 2(1): 111-122.
Li Chun-sheng, Yang Wei, and Wang Peng-bo. A review of spaceborne SAR algorithm for image formation[J]., 2013, 2(1): 111-122.
[7] 邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1-10.
Deng Yun-kai, Zhao Feng-jun, and Wang Yu. Brief analysis on the development and appliecation of spaceborne SAR[J]., 2012, 1(1): 1-10.
[8] Cristallini D, Pastina D, Colone F,.. Efficient detection and imaging of moving targets in SAR images based on chirp scaling[J]., 2013, 51(4): 2403-2416.
[9] 曾海彬, 曾涛, 李涛. 聚束式SAR斜视模型子孔径CS算法[J]. 北京理工大学学报, 2006, 26(4): 349-352.
[10] 黄源宝, 保铮. 大斜视SAR成像的一种新的二维可分离处理方法[J]. 电子与信息学报, 2005, 27(1): 1-5.
[11] Abramowitz M and Stegun I A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [M]. New York: Dover, 1972: 771-802.
[12] Clemente C and Soraghan J. Approximation of the bistatic slant range using chebyshev polynomials[J]., 2012, 9(4): 682-686.
[13] Papoulis A. Systems and Transforms with Applications in Optics[M]. New York: McGraw-Hill, 1968: 203-204.
[14] Rivlin T J. An Introduction to the Approximation of Functions[M]. New York: Dover, 2003: 39-68.
[15] Mittermayer J, Moreira A, and Loffeld O. Spotlight SAR data processing using the frequency scaling algorithm[J]., 1999, 37(5): 2198-2214.
侯育星: 男,1987年生,博士生,研究方向为SAR成像算法.
陈士超: 男,1985年生,博士生,研究方向为雷达成像.
唐 禹: 男,1976年生,副教授,研究方向为SAR实时信号处理、雷达系统技术.
冯大政: 男,1959年生,教授,研究方向为自适应信号处理、阵列信号处理.
邢孟道: 男,1975年生,教授,研究方向为SAR成像、ISAR成像、InSAR成像.
A New Form of Chirp Scaling Algorithm Based on Chebyshev Polynomials in Synthetic Aperture Radar Imaging
Hou Yu-xing Chen Shi-chao Tang Yu Feng Da-zheng Xing Meng-dao
(,,’710071,)
A new form of Chirp Scaling (CS) algorithm based on Chebyshevpolynomials in Synthetic Aperture Radar is proposed in this paper. Instead of Taylor series expansion, the Chebyshevpolynomials is used to approximate the two-dimensional frequency spectrum of the
signal which leads to a more accurate spectrum. Then the mathematic model extracted from the optical system is exploited to confirm the scaling function for range cell migration correction. Moreover, the approximation errors have the bounded limitation which improve the focusing effect of edge point and increase the depth of focus of the scene. The results of simulations confirm the effectiveness of the proposed algorithm.
SAR radar imaging; Chebyshevpolynomials; Chirp Scaling (CS) algorithm
TN957.52
A
1009-5896(2014)11-2646-06
10.3724/SP.J.1146.2013.01624
侯育星 houyuxing205@163.com
2013-10-25收到,2014-07-18改回
国家自然科学基金优秀青年基金(61222108)资助课题
