相位噪声对时差估计的影响分析

钟 森 夏 威 何子述



相位噪声对时差估计的影响分析

钟 森 夏 威*何子述

(电子科技大学电子工程学院 成都 611731)

在到达时间差(TDOA)测量中，两异地接收站所配备的本振都会存在相位噪声，该相位噪声会影响时差测量的性能。该文分析了相位噪声对经典的互相关法时差估计无偏性的影响，同时推导了仅考虑相位噪声时TDOA估计精度的克拉美罗下限(CRLB)。并进一步得到了相位噪声与加性噪声都存在时的CRLB及其相对于加性噪声环境下的CRLB退化系数。仿真结果验证了理论分析的结果。

信号处理；到达时间差(TDOA)；相位噪声；克拉美罗下限(CRLB)；互相关法

1 引言

时差测量广泛应用于雷达、声呐、语音增强等信号处理领域。时差测量有很多种方法，如文献[1-5]等，但这些方法一般都假设用于时差测量的接收机是理想的接收机，接收机内部不会对接收到的信号间的时差关系产生影响。在高精度时差测量中信号非理想接收是不得不考虑的问题。为了具体说明非理想接收对时差测量的影响，本文着眼于辐射源信号到达两异地接收站的到达时间差测量，辐射源信号经过接收机内部的混频、采样等处理得到的观测信号间的时差关系将会受到两异地接收机内混频频率一致性误差、采样频率一致性误差、相位噪声等非理想因素的影响。

接收机内部的混频、采样等所需的时钟通常都来自于本地系统时钟，两不同接收机中系统时钟虽然标称频率相同，但其实际工作频率总会与标称频率存在偏差，且由于两系统时钟的各自独立运行，其各自的频率偏差也是不相同的。针对这样的情况，文献[6-8]分析了时钟频率相位误差对时差测量或时延估计的影响并给出了其解决办法，但是关于系统时钟的相位噪声对时差测量的影响分析，却很少有文献讨论该问题。直到2012年瑞典国防研究院(Swedish Defense Research Agency)的研究人员在文献[9]中用实验证实了相位噪声对时差测量的影响，并提出了利用非相干数据融合(Incoherent Data Fusion, IDF)的方法来减小相位噪声对时差测量的影响。虽然该文献提出了减小相位噪声对时差测量影响的方法，但是相位噪声对时差测量影响有多大并没有从理论上给出详细的分析。

为了从理论上分析清楚相位噪声对时差测量的影响，本文分析相位噪声对经典相关法[1]时差估计无偏性的影响，并给出了相位噪声下时差估计精度的克拉美罗下界(Cramér-Rao Lower Bound, CRLB)，并与加性高斯白噪声(Additive White Gaussian Noise, AWGN)下时差估计的CRLB进行比较，在相位噪声与加性噪声下CRLB相同的准则下，得出了相位噪声功率与加性噪声功率间的等效关系式，通过这一关系式可以直接计算出该相位噪声对应多大加性噪声对时差测量的影响，以便在系统设计时方便时钟器件的选择以及时差测量精度的分析。在此基础上，本文进一步推导得到了相位噪声与AWGN同时存在时的时差估计CRLB，以及该CRLB相对AWGN环境下的CRLB间的退化系数闭式表达式。通过相位噪声与AWGN都存在时的CRLB表达式，可以更准确地分析时差测量的理论精度。通过退化系数表达式，可以计算出系统所选用的时钟器件会对时差测量精度造成多大的影响。另外，这些理论分析结果也可以帮助工程人员按照时差测量精度指标选定系统时钟。本文也给出了在典型时差估计方法下的仿真结果，通过比较该仿真结果与理论分析结果，进一步说明了本文理论分析结果的适用范围。

2 相位噪声下时差测量模型

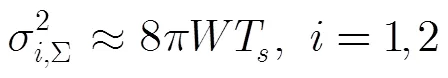
3 相位噪声对相关峰的影响

传统的时差测量通常通过搜索两路接收信号相关峰所对应的时延位置来测量时差[1]，本段通过在相位噪声出现时推导相关函数的表达式来考察相关峰是否受到影响以及受到怎样的影响。在信号模型式(2)下，两观测信号的相关函数为

由维纳过程的平稳独立增量过程特性及增量服从高斯分布的特性，并利用高斯概率密度函数的积分等于1的性质得到结论：

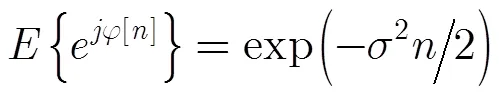
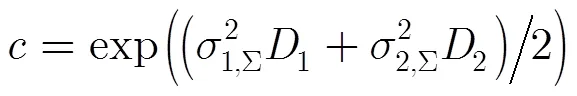
4 相位噪声下时差估计的CRLB

第3节讨论了在相位噪声下时差估计的均值性能，本节将讨论时差估计的均方误差(Mean Square Error, MSE)性能，也即是时差测量的精度。对于无偏估计精度的理论极限通常采用CRLB来进行描述，下面给出了其具体的推导过程与结论。

在相位噪声环境下时差估计的CRLB推导中，暂不考虑加性噪声，对观测数据模型式(2)，取相角得到

图1 不同相位噪声功率下的指数调制函数初始时刻的值

这里

定义矢量

根据先前的无噪信号确定性假定与维纳相位噪声假定，建立最大似然函数式(21)为

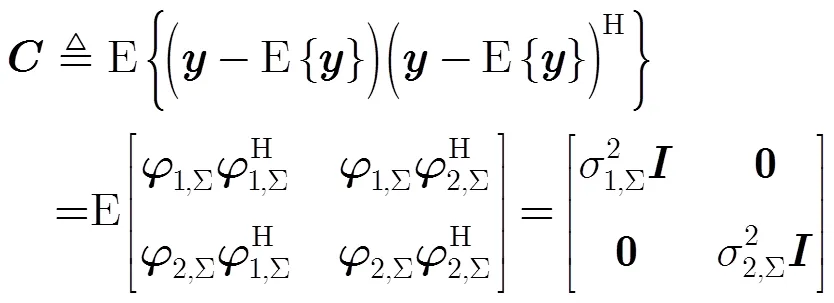
由式(22)、式(23)与式(25)，推导得到

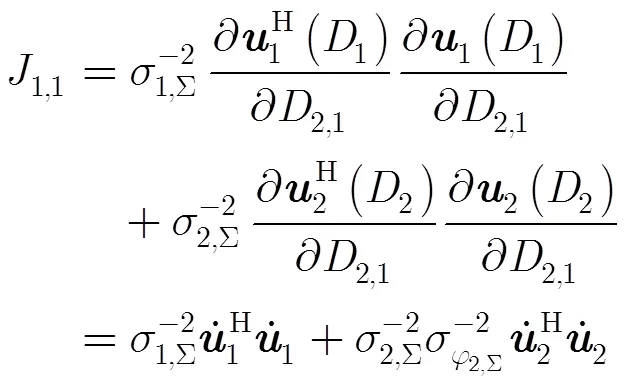
这里

于是得到乘性相位噪声下时差估计的CRLB为

5 相位噪声与加性噪声下的CRLB

在加性噪声模型下，时差估计的CRLB为[16]

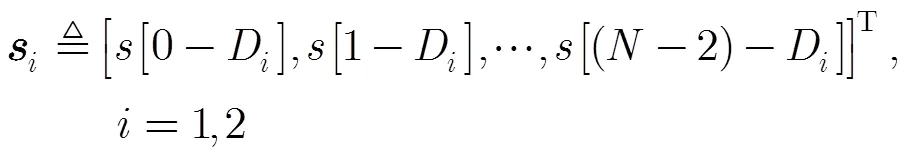
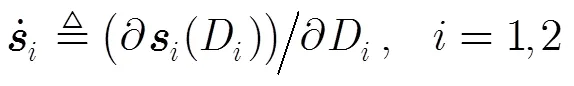
在信号数据足够长的情况下近似为

且进一步假定两观测信号的相位噪声功率相同(在选用同型号同批次的本振，这个条件可近似满足)，加性高斯白噪声的功率也相同(这个条件在接收机软硬件系统相同时也可近似满足)，根据式(28)与式(29)可分别得到乘性相位噪声环境与加性高斯白噪声环境下的CRLB为

由式(34)等于式(35)得到

也即是相位噪声的方差与加性高斯白噪声的方差满足式(36)时，其分别单独作用下的时差估计的CRLB相同。由于无法直接推导相位噪声与加性噪声同时作用下的CRLB，这里利用等效关系式(36)，将相位噪声的功率等效为加性噪声后进行相位噪声与加性噪声同时作用下的CRLB等效计算，由于相位噪声与加性噪声相互独立，所以其共同作用时的等效加性噪声功率为

于是等效的CRLB为

从而可以用式(38)来确定在一定相位噪声功率与加性噪声功率下时差估计的理论精度下限以指导时钟器件的选择以及系统时差测量指标的确定等。

相位噪声与加性噪声同时存在下的CRLB与仅存在加性噪声下的CRLB间的关系可写为

为了直观的说明式(38)给出的CRLB及式(40)给出的退化系数，这里采用零中频FM信号(基带未解调FM信号)来进行数值试验，以展示CRLB与相位噪声功率及AWGN噪声功率的关系。试验中零中频FM信号由式(41)产生

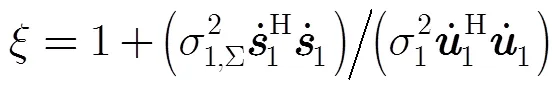
图2给出了在相位噪声与加性高斯白噪声环境下的CRLB，可见在加性噪声功率不变时，相位噪声功率越大，时差估计的CRLB越大，而在相位噪声功率不变时，加性噪声功率越大时差估计的CRLB越大。

表1不同时差测量精度对相位噪声功率的要求

时差测量的RMSE (单位：ns)100200400800 (单位：rad)0.00360.00740.01480.0296

6 仿真比较

为了直观的展示相位噪声对时差估计的影响，这里仿真了仅存在相位噪声下的时差估计与仅存在加性噪声下的时差估计。图4绘制了根均方误差(Root Mean Square Error, RMSE)相等时相位噪声与加性噪声功率等效关系曲线；该图同时给出了单独考虑相位噪声(此时不考虑AWGN)与AWGN(此时不考虑相噪)时，获得相同CRLB，所对应的相位噪声功率与AWGN功率间的关系。如图4所示，在高SNR条件下(AWGN功率较小时)，相关峰搜索法仿真结果与CRLB的理论预测结果更为接近；而在低SNR条件下(AWGN功率较大时)，仿真结果明显偏离了CRLB理论预测结果。这一现象也反映了CRLB在SNR较高时能较好地描述估计精度的理论下限，而在SNR较低时CRLB并不是一个紧的下界。

图2 CRLB与相位噪声及加性高斯白噪声间的关系

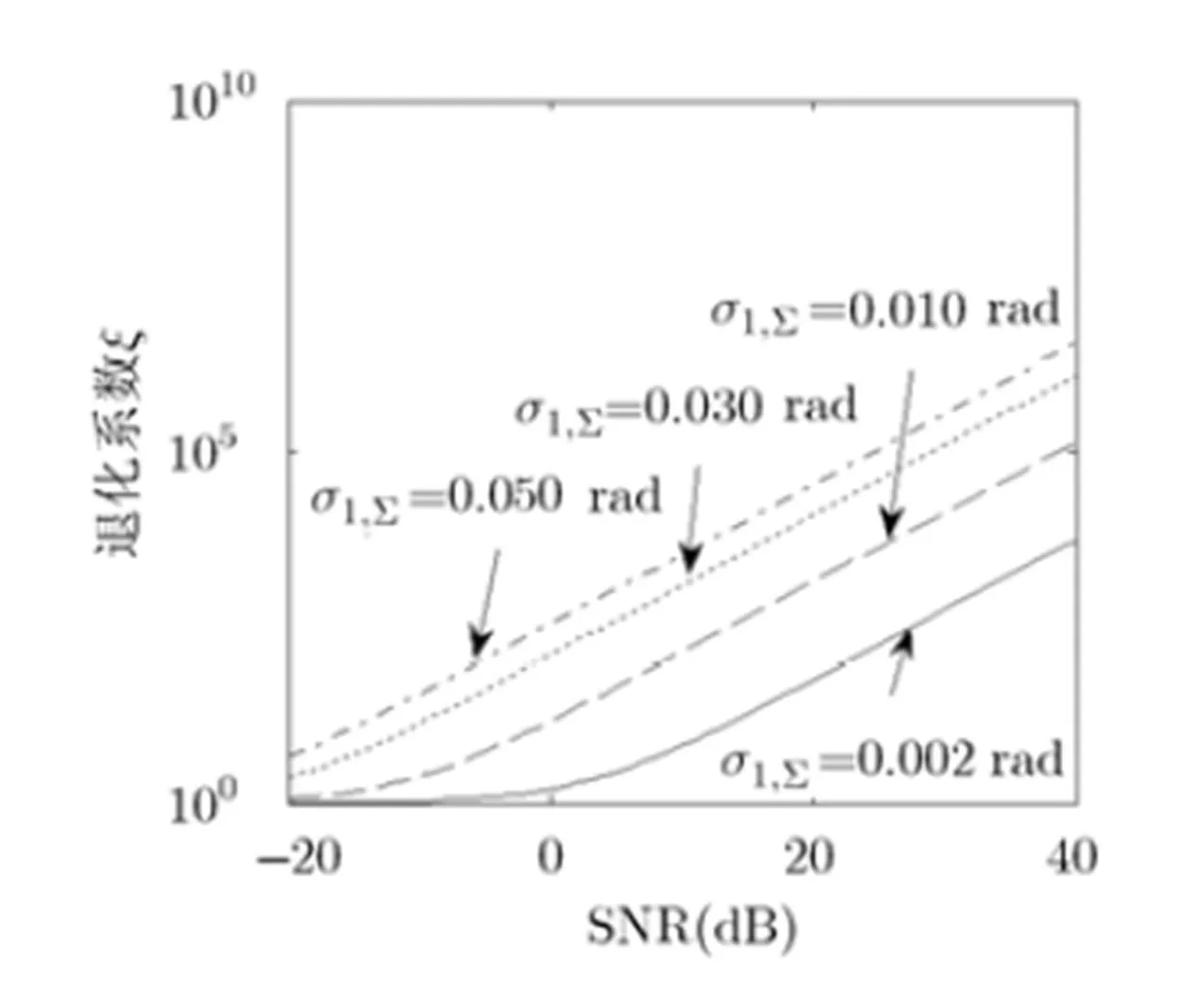
图3 不同相位噪声功率下的CRLB退化系数

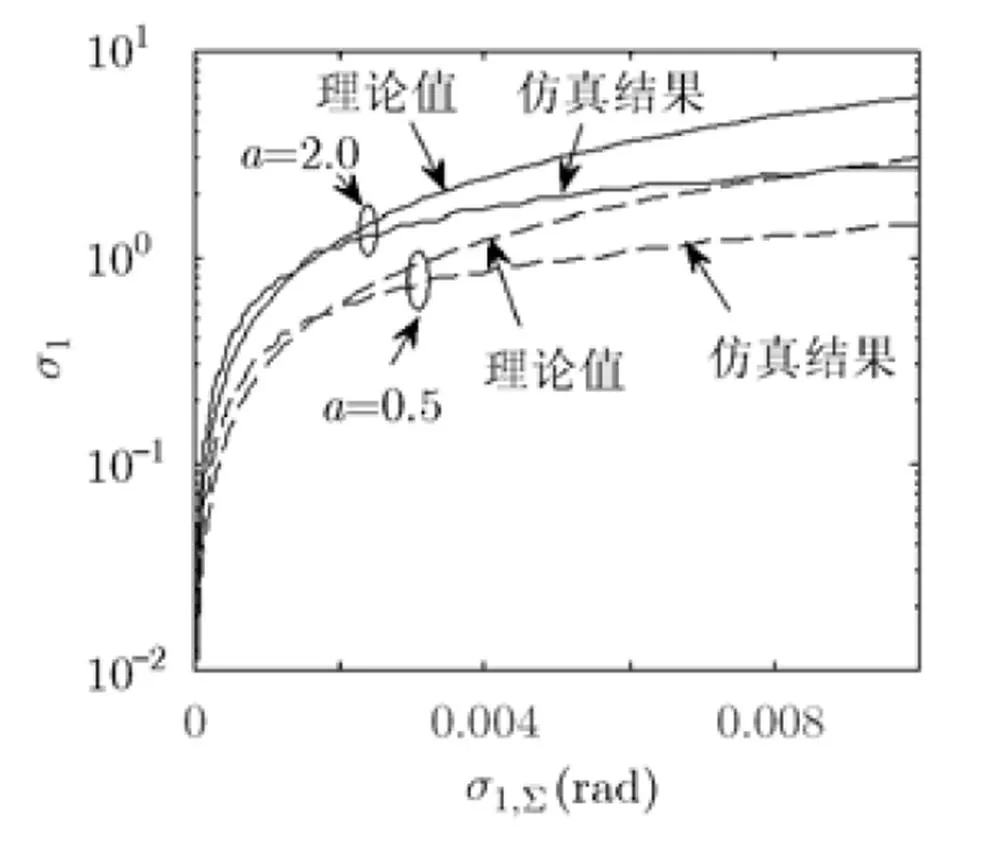
图4 相位噪声与加性噪声功率等效对应关系

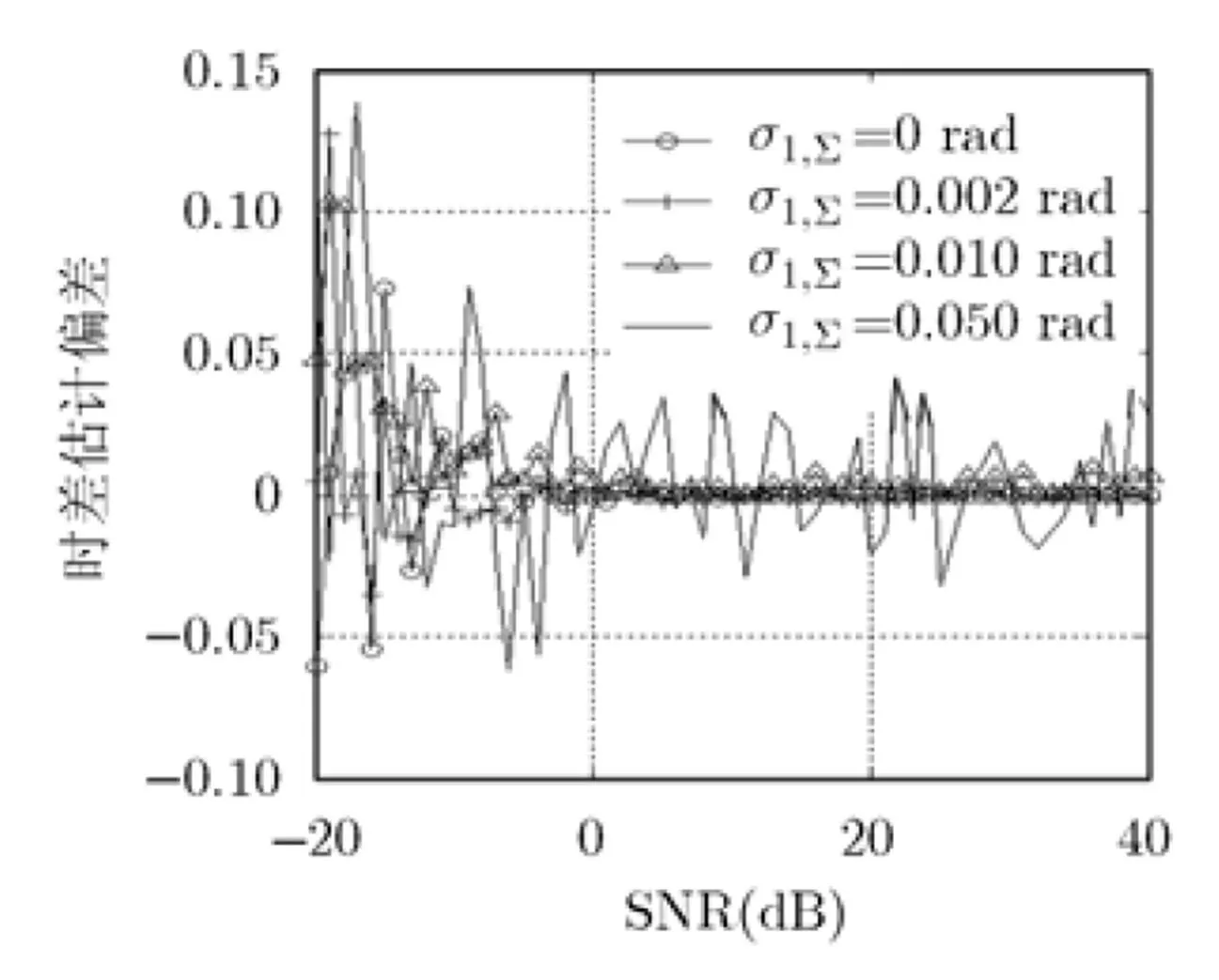
图5 时差估计的均值性能

图6 时差估计的RMSE与理论下限

从图6可以看出在仅存在加性噪声时RMSE的理论下限最小，随着相位噪声功率的增大，当SNR大于一定门限时RMSE理论下限几乎不再随SNR的增大而减小，并且该SNR门限会随着相位噪声功率的增大而减小。利用相关法估计时差的仿真结果也有类似的变化规律，且相关法时差估计仿真结果的RMSE在无相位噪声时与理论下限最靠近(SNR大于一定门限的情况下)，而在相位噪声出现时与理论下限间的距离变大2)。同时图6也反映了时差估计的RMSE与理论下限在高SNR环境下更接近的特点，这与图4中相位噪声功率与加性噪声功率较小时仿真结果与理论分析结果相对更接近的结论一致。

7 结束语

本文针对时差测量系统中时钟器件的相位噪声对时差测量的影响进行了理论分析，给出了时变的乘性相位噪声对时差估计准确度的影响，推导了时差估计精度的理论极限，并根据相位噪声与AWGN单独作用下的时差估计CRLB相等反推得到相位噪声功率与AWGN功率间的等效关系，并根据该等效关系得到相位噪声与AWGN都存在时的CRLB及其相对于AWGN环境下的CRLB的退化系数。并且通过典型算法的仿真结果与理论分析结果比较说明了理论分析适用范围。本文所得到的相位噪声与AWGN都存在情况下时差估计的CRLB可以用来评估不同时差估计算法性能的优劣，退化系数可以用来评估相位噪声对时差测量的具体影响，而相位噪声与AWGN功率等效对应关系可以在时差测量系统设计时用来指导时钟源器件的选择。

[1] Carter G C. Coherence and time delay estimation[J]., 1987, 75(2): 236-255.

[2] So H C, Ching P C, and Chan Y T. A new algorithm for explicit adaptation of time delay[J]., 1994, 42(7): 1816-1820.

[3] Ge Feng-xiang, Shen Dong-xu, Peng Ying-ning,Super-resolution time delay estimation in multipath environments[J]., 2007, 54(9): 1977-1986.

[4] Li X, Ma X, Yan S,Super-resolution time delay estimation for narrowband signal[J].,&, 2012, 6(8): 781-787.

[5] Jiang F, Kuang Y, and Astrom K. Time delay estimation for TDOA self-calibration using truncated nuclear norm regularization[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, Canada, 2013: 3885-3889.

[6] Falk J, Handel P, and Jansson M. Effects of frequency and phase errors in electronic warfare TDOA direction-finding systems[C]. Military Communications Conference (MILCOM), Boston, MA, USA, 2003: 118-123.

[7] Lin Jia-Chin and Hsu Heng-Yuan. Timing-delay and frequency-offset estimations for initial synchronization on time-varying Rayleigh fading channels[J]., 2013, 7(6): 562-576.

[8] Zhong Sen, Xia Wei, and He Zi-shu. Approximate maximum likelihood time differences estimation in the presence of frequency and phase consistence errors[C]. IEEE Symposium on Signal Processing and Information Technology (ISSPIT), Athens, Greece, 2013: 305-308.

[9] Johansson M and Hedstrom P. On the effect of tuner phase noise on TDOA measurements[C]. IEEE Communications and Information Systems Conference (MCC), Gdansk, 2012: 1-4.

[10] Ghozlan H and Kramer G. On Wiener phase noise channels at high Signal-to-Noise Ratio[C]. IEEE International Symposium on Information Theory Proceedings (ISIT), Istanbul, 2013: 2279-2283.

[11] Mehrpouyan H, Nasir A A, Blostein S D,.. Joint

estimation of channel and oscillator phase noise in MIMO systems[J]., 2012, 60(9): 4790-4807.

[12] Chorti A and Brookes M. A spectral model for RF oscillators with power law phase noise[J]., 2006, 53(9): 1989-1999.

[13] Demir A, Mehrotra A, and Roychowdhury J. Phase noise in oscillators: a unifying theory and numerical methods for characterization[J]., 2000, 47(5): 655-674.

[14] 陈良均, 朱庆棠. 随机过程及应用[M]. 第1版, 北京: 高等教育出版社, 2003: 78-81.

Chen Liang-jun and Zhu Qing-tang. Random Process and Its Applications[M]. First Edition, Beijing: Higher Education Press, 2003: 78-81.

[15] Kay S M. Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory[M]. Englewood Cliffs, NJ: Prentice-Hall, 1993: 23-52.

[16] Fowler M L and Hu X. Signal models for TDOA/FDOA estimation[J]., 2008, 44(4): 1543-1550.

钟 森： 男，1984年生，博士生，研究方向为时差测量与辐射源定位等.

夏 威： 男，1980年生，博士，副教授，硕士生导师，研究方向为自适应及阵列信号处理、雷达信号处理等.

何子述： 男，1962年生，博士，教授，博士生导师，研究方向为MIMO雷达、相控阵雷达信号处理等.

2)这是因为在AWGN环境下相关法时差估计是最优估计[1]，而当相位噪声出现时，相关法时差估计不再是最优估计。

Analysis of the Effect of Phase Noise on Time Difference Estimation

Zhong Sen Xia Wei He Zi-shu

(,,611731,)

In the Time Difference Of Arrival (TDOA) measurement system, the performance of time difference estimation degrades due to the inevitable presence of phase noises of local oscillators at spatially separated receivers. The effect of the phase noise on the unbiasedness of classic cross-correlation time difference estimator is discussed herein, as well as the Cramér-Rao Lower Bound (CRLB) of estimation is derived in the phase noise environment. Furthermore, the CRLB of time difference estimation in additive noise environment with phase noise considered is derived. The CRLB degradation coefficient with respect to the CRLB in the additive noise environment is also given. The theoretical analysis is validated by the simulation results.

Signal processing; Time Difference Of Arrival (TDOA); Phase noise; Cramér-Rao Lower Bound (CRLB); Cross-correlation method

TN911.7

A

1009-5896(2014)11-2614-07

10.3724/SP.J.1146.2013.01909

夏威 wx@uestc.edu.cn

2013-12-06收到，2014-04-15改回

国家自然科学基金(61101173)资助课题