基于序贯蒙特卡罗概率假设密度滤波的多目标检测前跟踪改进算法

占荣辉刘盛启 欧建平 张 军

(国防科学技术大学电子科学与工程学院 长沙 410073)

1 引言

在传统的目标跟踪中，通常先进行门限处理，从原始的观测中提取目标的量测信息，这种处理方法常被称为检测后跟踪(Detect-Before-Track,DBT)。DBT处理方法的潜在不足是，在进行门限处理过程中代表目标的有用信息可能被部分或全部舍弃，导致量测信息不完整(甚至有可能全部丢失)，这一问题在信噪比较低的条件下更为突出。为了提高低信噪比条件下的目标检测与跟踪能力，通常不事先设定门限，而直接对原始的观测数据进行处理，同时完成目标的检测与跟踪，这种处理方法又称为检测前跟踪(Track-Before-Detect, TBD)。

随着技术的发展，已有多种TBD算法被相继提出，这些算法按实现方式可粗略分为两大类，即批处理方法和递推型方法。作为批处理方法的典型代表如最大似然估计法[1]、动态规划法[2,3]等需要利用多个连续帧的数据，其算法复杂度通常较大。递推型方法(如贝叶斯推演)可有效降低运算开销，且不需要处理和存储多帧历史数据，这些优势使其具有更强的适应能力。贝叶斯推演的一种有效实现途径是序贯蒙特卡罗(Sequential Monte Carlo, SMC)，也称粒子滤波方法[4,5]，这种方法在单目标TBD背景下已有广泛深入的研究。

文献[6]给出了一种利用粒子滤波实现多目标TBD的典型应用实例，文中通过设计转移矩阵对目标个数的变化进行建模，并通过实验证实该算法对具有两个目标的特定应用条件是非常有效的。其不足之处是很难推广到更一般的多目标TBD应用条件，且不能适用于最大目标数目事先未知的场合。

在目标数目未知且具有时变特性的应用条件下，有限集统计量为多目标滤波提供了完整的贝叶斯推演手段，且这种推演是建立在随机有限集(Random Finite Set, RFS)理论[7,8]基础之上的。作为多目标贝叶斯滤波的一种矩近似求解手段，概率假设密度(Probability Hypothesis Density, PHD)滤波器[911]-自提出以来就受到持续的关注，且其SMC实现方式因具有理论上可证明的收敛特性[12]而被广泛应用。

在文献[13]中，首次将PHD滤波思想引入到红外图像多目标TBD应用中，通过建立目标运动模型和观测模型，利用SMC方法实现对未知数目的多目标进行检测与跟踪，算法中完整融入了跟踪的思想。不过，尽管文中的算法对非标准点目标模型具有适应性，对目标个数的估计却是有偏的。针对这一问题，文献[14]对粒子的权值更新算式进行了修正，改善了估计效果。但是，作为一种新的理论方法，现有的基于SMC-PHD算法在TBD应用条件下还存在以下3个突出问题：(1)用于近似目标状态的有效粒子数少，效率低；(2)算法复杂度高，时间消耗大；(3)目标状态提取不准确，稳定性差。为此，本文在现有研究的基础上提出了一种基于SMC-PHD的多目标TBD改进算法，该算法通过自适应粒子产生机制使粒子在潜在的目标区域聚集，进而通过粒子子集分割手段加速运算，最后经动态聚类方法实现多目标状态的准确提取。仿真结果验证了所提方法的优越性。

2 系统模型

在多目标条件下，目标t的运动状态可表示为

目标的强度可用传感器的点扩散函数建模为

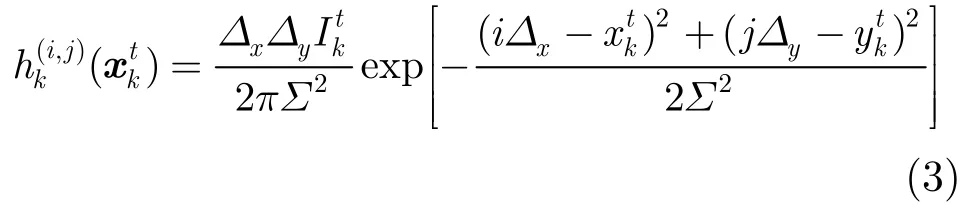
在高斯噪声假设下，式(4)可进一步记为

由于目标的响应仅能对其所处位置及其邻近网格单元有较显著的影响，因此似然函数可进一步近似为

3 基于SMC-PHD的TBD算法

由此可得预测粒子的权重为

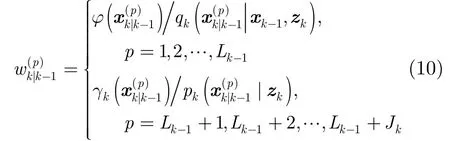
进一步通过 PHD的更新方程可完成粒子权值的更新。注意到在量测中，仅那些紧邻的分辨单元受到较大的影响，因此似然比可计算为

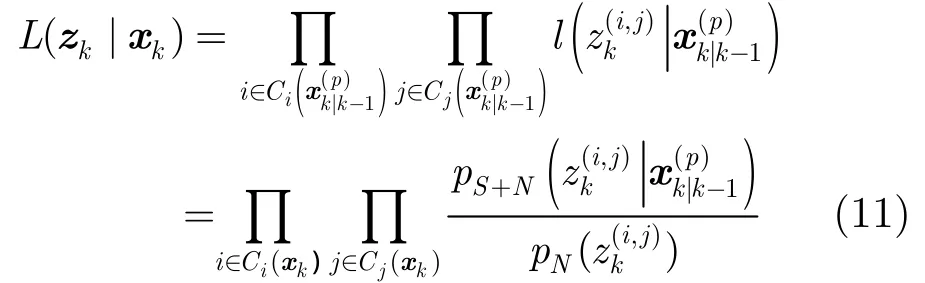
在文献[13]最初给出的基于SMC-PHD的TBD算法中，提供了一种权值更新的经验算式。

式中

由式(12)～式(14)的计算式可以看出，文献[13]在计算更新权时仅考虑了那些与待处理粒子具有相同支撑域的粒子，这对于传统的点目标模型来说是合适；但对于具有扩散效应的观测模型，这种处理方法会导致目标数目的过估计。为了详细说明这一点，假定由状态引起的有效量测可表示为，显然在TBD处理中，应将整个而不是某一特定的分辨单元作为目标引起的量测。因此，对于某一特定的粒子而言，其似然比需用更准确的式子表示为

相应地，式(13)中的ψ值应修正为

得到k时刻的更新权值后，相应的后验密度可表示为

在此基础上通过粒子重采样和聚类处理，即可实现递推滤波和目标状态提取。

4 SMC-PHD TBD算法改进

4.1 自适应粒子生成

在基于SMC的TBD算法中，一个重要的问题是如何有效地产生粒子来近似目标的真实状态分布。通用的做法是在整个监视区域均匀地散布粒子。这种方法的缺点是大量的粒子将被浪费在无效的近似上，因为这些粒子只占有微小的权重。另一种是数据驱动型方法，即采用量测数据来产生建议分布。在文献[13]中，将粒子均匀分布在像平面的感兴趣区域，感兴趣区域定义为观测强度大于某一预设门限Th的分辨单元，即。相比前面提及的通用做法，这种方法在某种程度上提高了粒子使用效率，但是量测信息仍没有被充分利用。

事实上，为了更好地近似目标的状态分布，人们总希望能自适应地产生粒子，一种可行的方案是根据目标的存在概率按比例分配粒子。在这种思路启发下，本文引入了一种新的代表新生目标的粒子产生策略，即首先通过强度量测信息对目标所在的分辨单元进行初始定位，而后通过粒子权值计算来评估目标的存在概率，最后通过重采样实现粒子的自适应分配。

具体地，假设将一部分观测强度较大的分辨单元(代表了潜在目标可能的位置)记为，则在这些分辨单元附近均匀分配粒子，且位置、速度和强度分量分别为

并对其进行归一化：

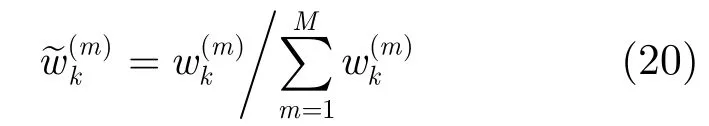
最后对粒子进行重采样得

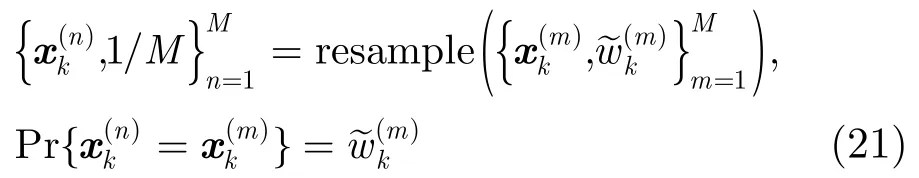
式中可采用不同的重采样方法，如系统重采样、残差重采样等。

经重采样后，代表新生目标的粒子将自动地向真实目标所处的位置聚集，从而能更好地近似多目标状态的后验密度。为了防止粒子过于集中可能导致的滤波性能下降问题，可在粒子重采样之后添加随机噪声扰动来保持粒子的扩散特性。

4.2 SMC高效实现

通常，为了得到多目标状态后验密度的良好近似，所需的粒子数目较大，相应地算法的运算开销也会非常大。这是因为在式(16)中，计算每一个粒子的更新权时，都需要对粒子集里的所有粒子进行一次似然比计算。不过，由PHD滤波的收敛性不难推知，经PHD预测和更新后，粒子将向真实目标所在的位置聚集。这就意味着，由粒子引起的有效量测(包含潜在目标的量测)数目不会太大，这是因为代表同一目标状态的粒子将近似占有相同的图像分辨单元。在这种假设前提下，通过对粒子全集进行子集分割处理，可达到TBD算法快速实现的目的。下面将给出所提方法的具体实现过程。

再对式(22)的位置分量进行离散化处理得到其在像平面中的分辨单元，即

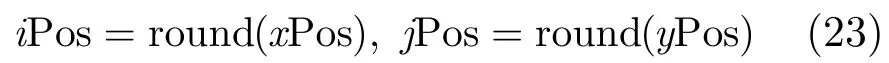
最后通过对粒子进行集合归并处理实现子集分割

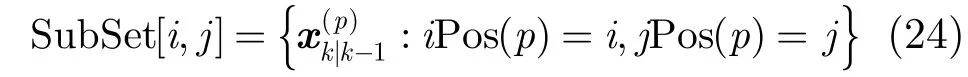
SMC高效实现方法的关键步骤可用表1中的伪代码表示。

表1 粒子权值更新的高效实现方法

4.3 目标状态提取

在基于SMC-PHD的TBD算法中，需要从后验密度中提取目标状态，这主要通过粒子聚类来实现。常用的聚类方法为k-means算法[15]，即先通过更新后的粒子权值得到目标个数的估计为整数)，再根据类间距离最小准则将全体粒子集聚成类，取每一类的聚心作为目标状态的估计。这种方法的不足主要体现在两方面：一是需要利用聚类数目先验信息，目标个数估计不准确将直接导致状态提取错误；二是需初始化聚心，聚心选择不恰当同样将导致聚类错误。为此本文提出了一种动态聚类算法，该算法可不事先指定聚类数目，利用粒子的聚集特性及其在像平面中的分布规律实现自动聚类。

具体地，对于k时刻经重采样后的粒子，分别提取出其x轴、y轴坐标分量和，并按升序进行排列得到对应的序列和，而后对其进行一阶差分处理得到,。

显然，对于同一个聚类，由于其扩散方差有限，因此将可容许的类内间隔定义为和。若同时满足，则将所有的粒子聚成一类；否则以和中超过门限,的元素个数作为各分量的类别数进行聚类。在此基础上判断原始粒子的坐标分量属于哪个聚类，得到类属矩阵。该矩阵中行向量不同的元素个数即为2维位置坐标总的聚类数，而行向量相同的元素序号(类属矩阵的行号)所对应的粒子即可组成一个独立的聚类。

通常情况下，经上述处理后即可完成粒子的准确聚类，实际应用中为了进一步提高目标状态提取的可靠性，可对每一个粒子聚类进行再次判断，将粒子个数小于某一门限的聚类剔除。这是因为，经重采样之后，所有的粒子具有相等的权重，若某一聚类中的粒子个数过少，说明其权值之和较小，不能代表一个真实的目标，因此需将其视为虚假聚类进行剔除。

5 仿真实验

本节将给出多目标TBD的应用实例，仿真中假定目标运动满足近匀速模型，而目标强度则采用随机游走模型，其状态方程可描述为

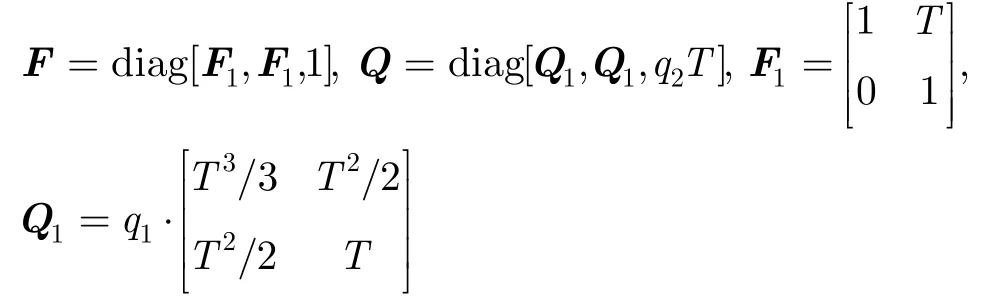
表2 基于SMC-PHD的TBD仿真参数

自适应粒子采样策略的有效性可通过图1中的结果进行说明，图中给出的是条件下的仿真示例。在图 1(a)中，粒子被均匀散布在潜在目标所处的 20个网格分辨单元附近(扩散方差取为，粒子占据了大部分监视区域，说明该粒子分配方法的效率是较低的。这是因为大量的粒子被分配到了并未出现真实目标的分辨单元，而代表真实目标状态的粒子(有效粒子)数目极少，对目标状态的近似效果不佳。相比之下，采用文中的自适应粒子产生机制以后，绝大部分粒子聚集在真实目标所处的位置附近，如图1(b)所示，该结果是先通过对粒子权值进行评估，进而采用重采样技术实现粒子再分配得到的。由此可见，自适应采样方法存在两大明显的优势：(1)几乎所有的粒子都用于近似真实的目标状态，近似精度高；(2)粒子具有良好的聚集性，为后续基于SMC-PHD的TBD算法高效实现创造了有利条件。

为了进一步说明峰值像素点选择方法的合理性(即不会使潜在的目标遗漏)，仍采用k=1时的场景设置，动态调整峰值点的个数，考察10000次Monte Carlo仿真中所选择的峰值像素点成功包含两真实目标的次数与总的仿真次数的比率(这里视为目标的成功检测率)，所得结果如图2所示。由此可见，在本文给出的仿真条件下，当峰值点个数取为 20时，成功检测到目标的概率为 1，说明通过该方法来产生粒子不会导致目标漏检。

图3～图5给出了目标初始强度I=30条件下的单次实验结果，其中图3为目标个数估计，图4为不同方法提取的目标状态，图5为相应条件下的最优子模式分配(Optimal Sub-Pattern Assignment,OSPA[16])距离误差。由图4中的结果可以清楚地看出，即便是在目标个数估计完全正确的情况下，通过传统k均值(k-means)聚类方法提取到的状态仍存在部分错误，从而导致图5中某些时刻的OSPA距离误差显著增大。究其原因，是因为k-means算法存在初始化环节，初始聚心选择不当将直接导致聚类错误。为详细说明这一点，图6进一步给出k=21时的单步仿真结果，其中虚线箭头指向k-means算法得到的聚类结果，实线箭头指向本文算法得到的聚类结果。由此可以看到，由于在随机初始化过程中k-means算法将2个聚心错误地选择在同一粒子云中，最终得到错误的聚类结果。而文中所提的聚类方法因利用了目标位置的有序差分信息，可有效克服这一问题，聚类结果完全正确(每一粒子云团得到一个与其完全对应的、代表真实目标的聚类)。

图7进一步给出了I=20条件下100次实验得到的平均OSPA距离误差。由图可见，在新目标出现时刻，由于目标检测可能存在一定的时延(在目标信号强度较弱的情况下这一问题将更加突出)，导致估计误差出现短暂上升(这是时变多目标跟踪中的一种普遍现象)。不过，文中所提算法的性能一致优于传统方法，这种优势的获得主要源于两方面原因：(1)当两种算法都能得到目标个数的准确估计时，所提算法因具有更好的目标状态近似能力而呈现出更小的状态估计误差；(2)与传统的k-means聚类方法相比，文中所提算法降低了错误提取目标状态的可能性，从而降低了OSPA距离误差。

图1 基于峰值单元的新生粒子产生方法

图2 不同条件下的目标检测概率

图3 目标个数估计结果

图4 目标状态提取结果

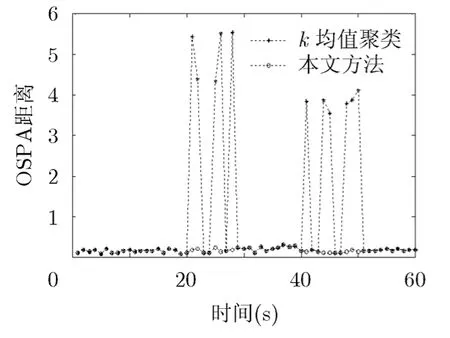
图5 OSPA距离误差比较

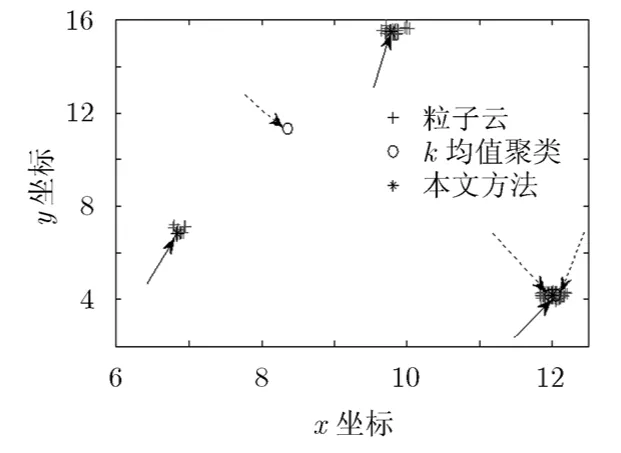
图6 k=21时的目标状态提取结果

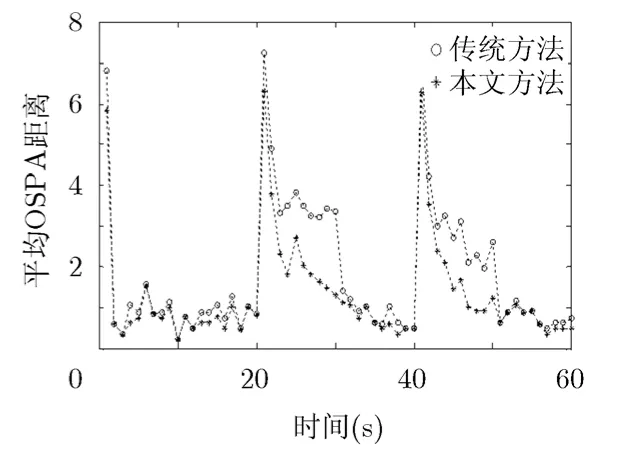
图7 平均OSPA距离比较

两种不同实现方式下的算法运算开销(CPU时间)如表3所示。表3中的传统实现方式，指的是根据式(16)对所有的粒子逐一地计算概率生成泛函ψ，并通过式(12)进行粒子权值更新的计算方法。而文中所提的快速实现方式指的是先通过自适应机制产生粒子，再利用 4.2节所述的子集分割策略进行ψ值计算和粒子权值更新的方法。仿真是在通用PC机中完成的，系统配置为2.0 GHz双核CPU, 2.8 GB RAM，仿真软件为Matlab7。由表中的结果可以看出，本文所提快速算法的执行效率(单次仿真的平均耗时)比传统实现方式要高得多，且在仿真参数设置条件下可以做到实时处理。运算效率的大幅提高主要是通过自适应粒子产生机制使粒子聚集在某些特定的单元，在此基础上根据图像分辨单元将全体粒子集划分成有限子集来处理而实现的。

表3 不同实现方式的时间消耗(s)

6 结束语

本文针对红外传感器目标探测应用背景，提出了一种基于SMC-PHD的时变多目标TBD改进算法。该算法通过引入自适应粒子产生机制改善了粒子的聚集程度及对新生目标状态分布的近似精度，并利用粒子集分割技术提高了算法的执行效率，最后通过粒子动态聚类方法减小了目标状态的提取误差。需要指出的是，文中所提的方法仅利用了图像的帧内信息，如何进一步挖掘图像的帧间信息来提高多目标TBD性能是个值得探索的问题，也是下一步的研究方向。

[1] Tonissen S M and Bar-Shalom Y. Maximum likelihood trackbefore-detect with fluctuating target amplitude[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998,34(3): 796-809.

[2] 郑岱望, 王首勇, 杨军, 等. 一种基于二阶Markov目标状态模型的多帧关联动态规划检测前跟踪算法[J]. 电子与信息学报,2012, 34(4): 885-890.

[3] Grossi E, Lops M, and Venturino L. A novel dynamic programming algorithm for track-before-detect in radar systems[J]. IEEE Transactions on Signal Processing, 2013,61(10): 2608-2619.

[4] Arulampalam S, Maskell S, Gordan N, et al.. A tutorial on particle filter for on-line nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002,50(2): 174-188.

[5] Davey S J, Rutten M G, and Cheung B. Using phase to improve track-before-detect[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 832-849.

[6] Boers Y and Driessen J N. Multitarget particle filter track before detect application[J]. IEE Radar, Sonar and Navigation, 2004, 151(6): 351-357.

[7] 熊波, 甘露. MM-CBMeMBer滤波器跟踪多机动目标[J]. 雷达学报, 2012, 1(3): 238-245.

[8] Mahler R. Multi-target Bayes filtering via first-order multi-target moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[9] Lin L K, Xu H, Sheng W D, et al.. Multi-target state-estimation technique for the particle probability hypothesis density filter[J]. Science China (Information Sciences), 2012, 55(10): 2318-2328.

[10] Nannuru S, Coates M, and Mahler R. Computationallytractable approximate PHD and CPHD filters for superpositional sensors[J]. IEEE Journal of Selected Topic in Signal Processing, 2013, 7(3): 410-420.

[11] Habtemariam B K, Tharmarasa R, and Kirubarajan T. PHD filter based track-before-detect for MIMO radars[J]. Signal Processing, 2012, 92(1): 667-678.

[12] Clark D and Bell J. Convergence results for the particle PHD filter[J]. IEEE Transactions on Signal Processing, 2006,54(7): 2652-2661.

[13] Punithakumar K, Kirubarajan T, and Sinha A. A sequential Monte Carlo probability hypothesis density algorithm for multitarget track-before-detect[J]. SPIE, 2005, 5913: 1-8.

[14] 林再平, 周一宇, 安玮. 改进的概率假设密度滤波多目标检测前跟踪算法[J]. 红外与毫米波学报, 2012, 31(5): 475-480.

[15] Clark D and Bell J. Multi-target state estimation and track continuity for the particle PHD filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4):1441-1453.

[16] Schuhmacher D, Vo B-T, and Vo B-N. A consistent metric for performance evaluation of multiobject filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.