结合非连续性测度的方向偏微分方程在电子散斑干涉中的应用

肖志涛 袁 泉 张 芳吴 骏 耿 磊 冯铁君 陈 颖 王丹钰

(天津工业大学电子与信息工程学院 天津 300387)

1 引言

电子散斑干涉测量技术(Electronic Speckle Pattern Interferometry, ESPI)是一种无损检测技术，可测量物体表面各点的位移量或应变量[1]。但电子散斑干涉条纹图中伴随着强烈的噪声，不利于后续的二值化、骨架线提取[2]等处理，因此条纹图的滤波具有重要意义。

条纹结构具有明显的方向性，在滤波的过程中考虑条纹的方向性至关重要[3]。根据条纹图方向性特点，近年来人们提出了许多新的条纹图滤波方法。文献[4]提出通过跟踪条纹方向获得等值线窗口，然后在此窗口内对条纹图进行滤波。文献[5]将条纹的方向融入偏微分方程(Partial Differential Equation,PDE)中提出了二阶方向偏微分方程滤波模型。此外，如果对整幅条纹图进行同等程度的滤波，势必会导致稀疏条纹处滤波程度不够而密集条纹处过分滤波的问题。因此，在考虑滤波方向的同时，还必须对不同位置像素点的滤波程度加以考虑。在这方面，文献[6]提出了PM方程，利用与图像梯度有关的扩散系数对扩散速率施加影响。但是电子散斑干涉条纹图中含有大量噪声，基于图像梯度设置扩散系数的方法必然受到噪声的影响。在图像分割领域，文献[7]提供了一种利用尺度理论，即非连续性测度(DisContinuities Measure, DCM)来检测图像中的区域同质属性的方法。本文借鉴非连续测度的思想，在方向偏微分方程的主体上加入非连续测度检测图像的特征，使得不同特征处滤波程度不同，以此来控制每一点的扩散速率。

2 基于方向的ESPI条纹图滤波方法

2.1 条纹图方向的求取

与自然图像不同，条纹图的方向特征显著。选取条纹图像中的一小块区域进行观察，能够发现相邻条纹近似平行，条纹的方向变化很微小，如图 1所示。当局部区域足够小时，稳定的方向性是条纹图的内在属性特征。在理想情况下，局部区域经 2维傅里叶变换[8]后，均匀分布的条纹转化为两个关于原点对称分布的亮斑。同时，亮斑的连线与条纹所在的方向相垂直。因此，可以根据频域中亮斑的位置来计算条纹方向。

实际的条纹图像并非严格的周期函数，并且当条纹图存在严重的噪声或者条纹对比度较差时，就会分散理想条件下形成的亮斑的能量。但是条纹图像的主要频率的能量在总能量中占绝大部分，而其他频率的能量较少。针对这种情况，可以采用概率论中求期望的方法来估算方向[9]。

图1 一幅无噪条纹图及其局部区域的频谱图

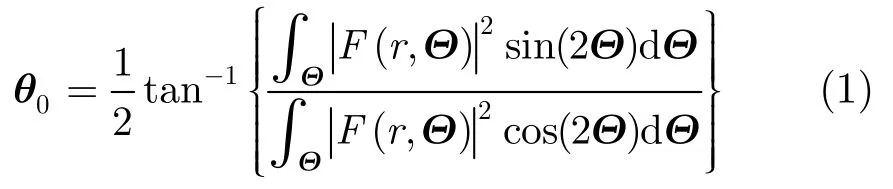
在初步计算得到条纹方向0θ后，需要对其进行平滑处理，可以采用3×3高斯滤波器进行滑动滤波，最终求得的条纹方向为θ。

2.2 二阶方向偏微分方程(SOOPDE)滤波方法

应用偏微分方程进行图像滤波是将图像滤波变换看作偏微分方程的算子，代入初始图像 ( )x,yI ，通过求解偏微分方程实现图像滤波[11]。由图2建立的内在坐标系知，理想的干涉条纹图在沿着条纹方向的灰度不变，所以为了充分滤除 ESPI条纹图中的噪声，应该加强此方向的灰度扩散，而为了保护条纹的信息，在条纹图的法向应减少扩散。二阶方向偏微分方程(Second-Order Oriented Partial Differential Equation, SOOPDE)充分利用条纹图的方向性，使方程仅沿着条纹方向进行滤波，其表达式为

图2 沿着条纹方向线和法向曲线示意图

SOOPDE仅考虑了条纹图的方向性，但是就整幅条纹图而言，各处的滤波程度是一样的。这势必会导致稀疏条纹处对噪声的滤波程度不够而密集条纹处过分滤波的问题。因此，在考虑滤波方向的同时，还必须对不同位置像素点的滤波程度加以考虑。Perona和Malik提出了PM方程[6]，利用与图像梯度有关的扩散系数对扩散速率施加影响。因此，结合扩散系数可以得到选择扩散方向偏微分方程(Selective Second-Order Oriented Partial Differential Equation, SSOOPDE)。

其中σG为3×3的高斯滤波器是卷积符号，c函数的表达式[12]为

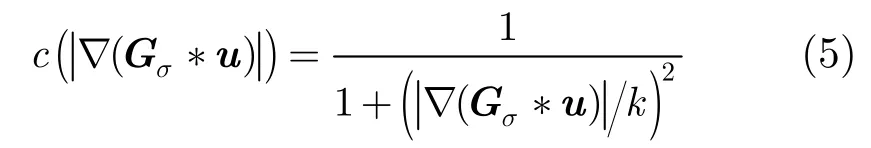
其中k为常数，c满足式(6)

3 结合非连续性测度的方向偏微分方程滤波方法

SSOOPDE滤波方法的基本思想是基于图像的梯度来设置扩散系数，控制图像中不同区域像素点的滤波程度，使像素的灰度值与图像局部特征相符。虽然SSOOPDE模型能够在一定的程度上解决条纹较稀疏地方的内部噪声处滤波程度不够而条纹较密集处过分滤波的问题，但是梯度特征对噪声敏感，检测不稳定，无法将噪声和重要特征区分开。

3.1 非连续性测度

文献[7]提出一种基于尺度的非连续性测度，用来描绘图像中的两点和所在区域的不连续性。

第1步 对给出图像中的任意像素，确定一个合适的邻域，其大小为，使得邻域中所有像素都满足一个灰度一致准则。

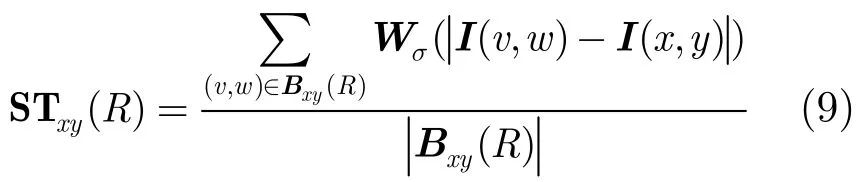
第2步 计算相邻两点相同大小的邻域中所有像素的对应灰度差。

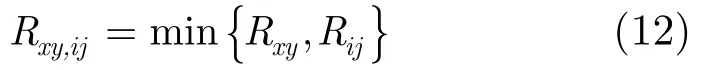
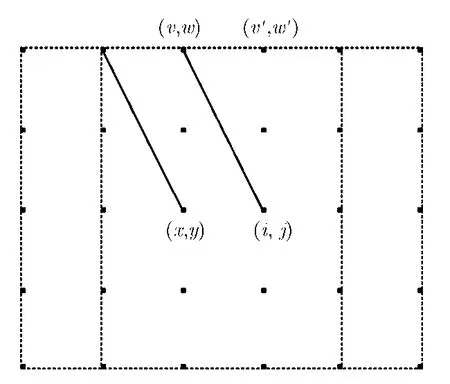
图3 两邻域对应关系

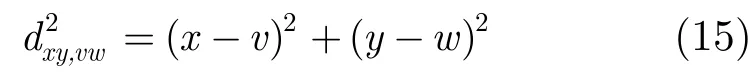
灰度正差为

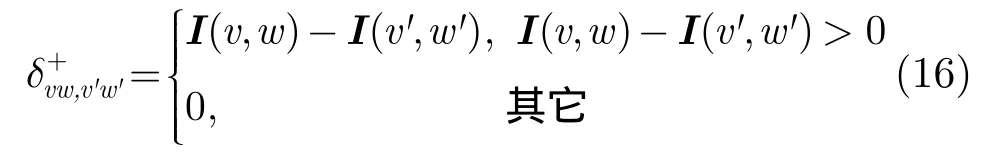
灰度负差为

累积灰度正差为

累积灰度负差为

第3步 计算每一点的非连续性测度。

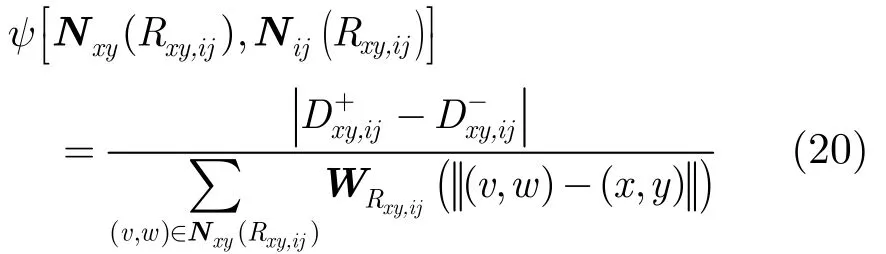
求取每一点的非连续性测度时，可根据式(20)分别计算当前点与其最小边界区域中的所有点的不连续性，然后取均值。因此像素点处的非连续性测度可表示为

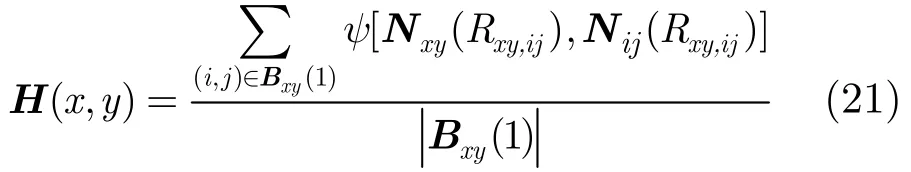
非连续性测度反映一个像素与其周围环境之间的不连贯性，取值范围为[0,1]。图 4展示了图像的梯度信息和非连续性的差异，第1列分别为含有脉冲噪声的自然图像和ESPI条纹图像，第2列和第3列分别显示了图像的梯度信息和非连续性测度。从图中可以看出，梯度对噪声非常敏感，而非连续性测度在区分噪声和图像特征方面具有明显的优越性，尤其是在条纹比较密集的情况下，非连续性测度具有很好的鲁棒性。由于非连续性测度能很好地区分噪声与图像的重要信息，本文利用非连续性测度来设置方向偏微分方程的扩散系数改善方程的滤波性能。

3.2 结合非连续性测度的方向偏微分方程滤波方法

基于方向的 PDE滤波方法形式简洁且偏微分方程的离散数值解法容易实现，故本文仍采用方向PDE的主体形式来实现滤波时对滤波方向的控制。利用像素的非连续性测度控制不同位置方程的扩散速率，本文提出结合非连续性测度的方向偏微分方程(DisContinuities Measure Oriented Partial Differential Equation, DCMOPDE)，具体形式为

其中H为上文提到的非连续性测度。该方程的基本思想是，方程仅在沿着条纹的方向进行滤波；同时在条纹密集处，扩散速率较小，保护条纹特征，在条纹稀疏的地方，扩散速率较大，进行充分滤波。

4 偏微分方程的离散数值解

利用偏微分方程进行图像处理是通过迭代求解方程实现的，因此处理前先要对方程进行离散化[13]。假设迭代时间步长为，在方程的迭代滤波过程中，迭代次数为时刻的演化图像可表示为。采用的时间差分为

采用的空间差分为

由此，可得结合非连续性测度的方向偏微分方程(DCMOPDE)的差分格式为

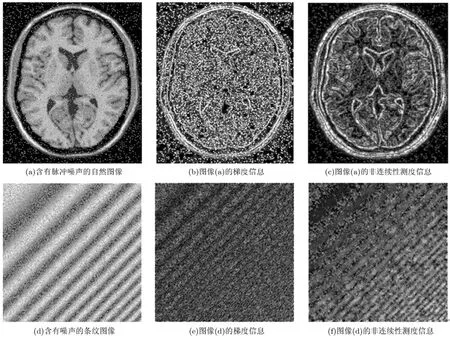
图4 梯度信息与非连续性测度的比较

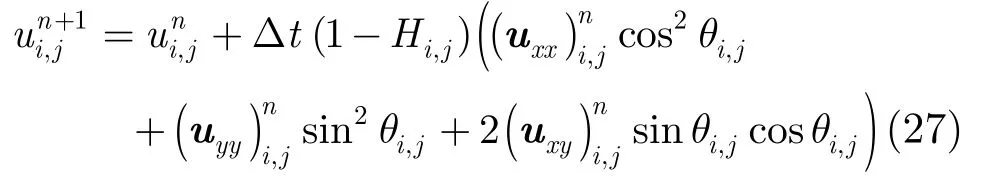
5 实验与结果分析

将本文方法用于电子散斑干涉条纹图，并与SSOOPDE进行比较。这里给出3组对比结果，包括两组模拟的条纹图和一组实验获得条纹图，离散求解方程时所采用的滤波参数为对于模拟条纹图(图5和图6)，，对于实验条纹图(图7)，。

模拟条纹图的生成方式[14]为

其中，0I为背景光强的幅值，1I为条纹光强的幅值，φ为条纹图的相位，nI为高斯噪声。通过设置不同形式的(,)x yφ，可以模拟不同形状的条纹图。

从3组对比结果可以看出，带非连续性测度扩散系数的方向偏微分方程式(22)能够有效控制不同特征像素点的扩散滤波速度，在充分滤除稀疏条纹处噪声的同时，有效保护密集条纹处的条纹信息，滤波效果优于基于梯度扩散系数的方向偏微分方程式(4)。

图5 一幅模拟的稀疏条纹图及其滤波结果比较

图6 一幅模拟的密集条纹图及其滤波结果比较

图7 一幅实验拍摄的条纹图及其滤波结果比较

为了更加客观地比较各模型的滤波结果，本文采用散斑指数和保真度两个参数来评估其性能，文献[15]中详细给出了这两个参数的计算方法。散斑指数s用来衡量滤波后条纹图像I的局部平滑程度。保真度f用来评价滤波后图像和理想的无噪声图像之间的差异，即滤波后图像对原始图像细节的保持程度。s越小，表明处理后图像的局部平滑程度越好，f越大，表明处理后图像越接近理想无噪声图像。评价结果如表1所示。由于图7是一幅实验图像，所以无法计算滤波后图像与理想图像之间的差异，即对于这幅图像无法计算各滤波结果的保真度。

表1 两种滤波模型的性能比较

从表1中的数据可以看出，结合非连续性测度的方向偏微分方程式(22)优于基于梯度的选择扩散方向偏微分方程式(4)，这说明DCMOPDE模型在滤除条纹图像噪声和保留图像重要特征方面都有显著的优势。

此外，本文采用的滤波参数是经验值，在所选参数下，方程是稳定的、收敛的，即能够得到正确的滤波结果。以图5所示的模拟条纹为例，计算过程中选取的迭代时间步长为 0.2，迭代次数为 30。本文分析了迭代过程中前后两次迭代结果均差(如式(29)所示，为图像的尺寸)的变化情况，结果如图8所示。从图8中可以看出，随着迭代次数的增大，前后两次迭代结果的均差是在逐步减小的，说明本文提出扩散方程是收敛的，同时本文选取的迭代时间步长满足方程的稳定性要求。此外，结合表1中列出的比较结果，迭代30次后，结果图像的散斑指数约为0.2，说明在此迭代次数下，图像已经平滑，方程的去噪效果良好。

图8 滤波过程中前后两次迭代结果的均差曲线

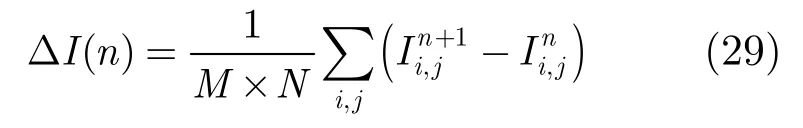
6 结束语

本文在方向偏微分方程的基础上，提出了结合非连续性测度的方向偏微分方程。该方法能够控制滤波方向，使滤波仅沿着条纹方向进行；同时本文方法能够有效控制不同特征像素点的扩散滤波速度，在充分滤除稀疏条纹处噪声的同时，有效保护密集条纹处的条纹信息。将本文方法应用于电子散斑干涉条纹图中，定性和定量分析均表明了本文方法是一种较好的条纹图预处理方法。

[1] Tang C, Wang L, Yan H, et al.. Comparison on performance of some representative and recent filtering methods in electronic speckle pattern interferometry[J]. Optics and Lasers in Engineering, 2012, 50(8): 1036-1051.

[2] 王新强, 张丽娟, 班宝龙. 基于滤波图像相减二值化的干涉条纹骨架线提取的研究[J]. 激光杂志, 2012, 33(6): 28-29.Wang Xin-qiang, Zhang Li-juan, and Ban Bao-long. Study on the extraction of interference fringes skeleton based on the binarization of the difference between filtering images[J].Laser Journal, 2012, 33(6): 28-29.

[3] 张芳. 散斑干涉信息提取技术及其应用研究[D]. [博士论文],天津大学, 2009.Zhang Fang. Speckle interferometry information extraction technology and application[D]. [Ph.D. dissertation], Tianjin University, 2009.

[4] Yang X, Yu Q, and Fu S. A combined method for obtaining fringe orientations of ESPI[J]. Optics Communications, 2007,273(1): 60-66.

[5] Tang C, Han L, and Ren H. Second-order oriented partialdifferential equations for denoising in electronic-specklepattern interferometry fringes[J]. Optics Letters, 2008, 33(19):2179-2181.

[6] Perona P and Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639.

[7] Saha P K and Udupa J K. Optimum image thresholding via class uncertainty and region homogeneity[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2001, 23(7): 689-706.

[8] 迟华山, 王红星, 郭奇, 等. 短时傅里叶变换在线性调频信号时频滤波中的应用[J]. 电讯技术, 2012, 52(2): 155-159.Chi Hua-shan, Wang Hong-xing, Guo Qi, et al.. Application of STFT in time-frequency filtering of LFM signals[J].Telecommunication Engineering, 2012, 52(2): 155-159.

[9] Chikkerur S, Cartwright A N, and Govindaraju V.Fingerprint enhancement using STFT analysis[J]. Pattern Recognition, 2007, 40(1): 198-211.

[10] Hong L, Wan Y, and Jain A. Fingerprint image enhancement:algorithm and performance evaluation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(8):777-789.

[11] 刘西林, 王泽文, 邱淑芳. 基于 Priwitt算子的偏微分方程图像去噪模型[J]. 计算机应用, 2012, 32(12): 3385-3388.Liu Xi-lin, Wang Ze-wen, and Qiu Shu-fang. PDE-based image noise removal models based on Priwitt operator[J].Journal of Computer Applications, 2012, 32(12): 3385-3388.

[12] Zhou X, Baird J P, and Arnold J F. Fringe-orientation estimation by use of a Gaussian gradient filter and neighboring-direction averaging[J]. Applied Optics, 1999,38(5): 795-804.

[13] Zhang F, Liu W, and Xia L. Homomorphic partial differential equation filtering method for electronic speckle pattern interferometry fringes based on fringe density[J]. Chinese Optics Letters, 2009, 7(3): 210-213.

[14] 邢月启. 图像去噪的偏微分方程方法研究[D]. [硕士论文], 西安电子科技大学, 2009.Xing Yue-qi. The research of partial differential equations for image denoising[D]. [Master dissertation], Xidian University,2009.

[15] Xiao Z, Xu Z, Zhang F, et al.. ESPI filtering method based on anisotropic coherence diffusion and Perona-Malik diffusion[J].Chinese Optics Letters, 2013, 11(10): 101101-1-101101-4.