使用不同置信级训练样本的神经网络学习方法

高学星 孙华刚 侯保林



使用不同置信级训练样本的神经网络学习方法

高学星*①孙华刚②侯保林①

①(南京理工大学机械工程学院 南京 210094)②(军械技术研究所 石家庄 050000)

针对含不同置信级样本的模型拟合问题，该文提出了一种基于神经网络的二次学习方法。文中指出真实模型是实验模型的一种变异，提出逼近真实模型期望值的神经网络，是融合先验样本和真实样本的最佳网络。首先，以先验样本为训练样本进行第1次神经网络学习，并计算取决于硬点信息的软点误差容量区间；然后，同时将先验样本和真实样本作为训练样本，利用软点误差容量区间和硬点误差敏感系数，对神经网络训练过程中输入/目标对的误差进行修改，通过第2次学习得到既能精确拟合真实样本，又能最大化利用先验样本信息的综合网络。与基于知识的神经网络(KBNN)相比，该方法更加简单，可操控性更强并具有更加明确的逻辑意义。

神经网络；模型拟合；基于知识的神经网络(KBNN)；先验知识

1 引言

机器学习算法在很多应用领域被证明很有使用价值，可以有效地解决数据挖掘等需要动态适应条件变化，或者超出人类当前认知范围的某些困难问题[1]。机器学习的效果严重依赖于训练样本的数量和质量[2]，通常，来自真实使用过程的真实样本比较稀少而且分布不全面，此时真实样本不适合直接用来建模[3]。1990年，文献[4]提出了联合符号化领域理论和神经网络的基于知识的神经网络方法(Knowledge-Based Neural Networks, KBNN)。与传统神经网络相比，KBNN提供了一种使用特定问题知识(problem-specific knowledge)来补偿样本缺少的学习途径[5,6]。KBNN在非线性动态建模[7]、控制[8]、监测诊断[9,10]、预测[11,12]和知识库的补充[13]等方面得到了应用。但总体来说，其应用并不广泛[14]，主要有两方面原因：对于复杂系统，先验领域知识不易获得，不准确的领域知识甚至会对算法造成误导[15]；另外，尚无证据表明神经网络的结构因素变化具有明确的意义[16]。

实际上，真实样本稀少时，不仅可以利用公式化的领域知识进行补充，实验样本作为数据形式的先验知识，同样可以与真实样本结合进行训练学习。可以将实验样本学习到的神经网络作为另一种形式的领域知识，应用KBNN对真实样本进行学习。KBNN会通过对初始网络权值进行一定范围内精化修正的方法实现对真实样本的进一步学习。

本文基于不同置信级样本(真实样本与实验样本)间的误差分析，针对含先验样本的拟合问题，提出了一种不同于KBNN的神经网络2次学习方法，通过修改标准神经网络算法中输入/目标对误差进行第2次训练，以获得融合先验样本和真实样本的综合网络。

2 基本思路

虽然实验或者虚拟实验更容易获得大量可规划的样本，但大多数情况下的实验模型相对真实模型都有一定的误差，该误差可能是因为实验条件的不完全真实性，或者样本的获取途径差异，所以真实样本和实验样本是具有不同置信度级别的。不妨称实验样本为软点样本，真实使用中获取的样本为硬点样本。若只简单地将二者合在一起进行神经网络训练，对于偏离软点的硬点，要么会导致过拟合，要么会成为被忽略的“噪点”。需要一种改进的训练算法，使其既能对硬点精确拟合，又能最大限度地利用软点提供的信息。

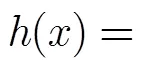
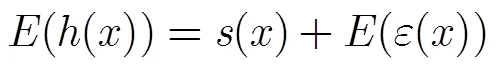
3 针对单硬点样本的拟合算法

3.1 单硬点样本的模型误差期望值分析

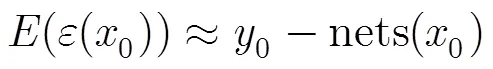
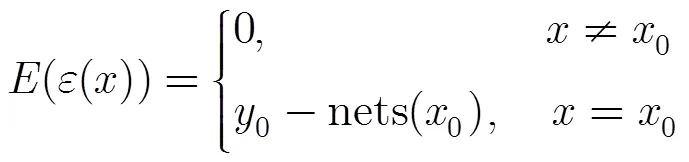
此时误差函数是离散的，没有“刚性”的。

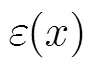
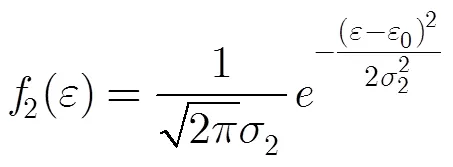
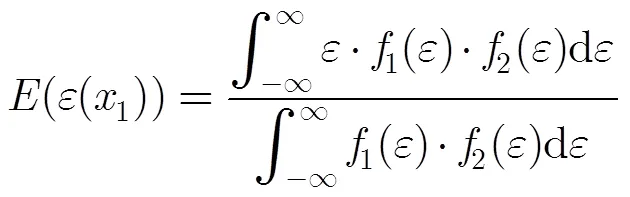
对上式进行整理得

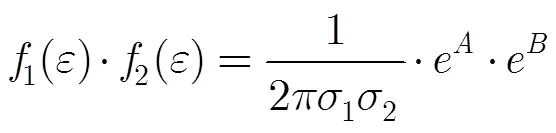
从而

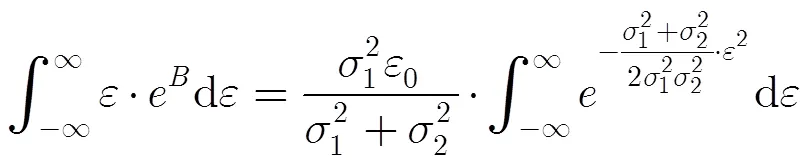
将式(8)和式(9)代入式(6)，约去相同项，可得

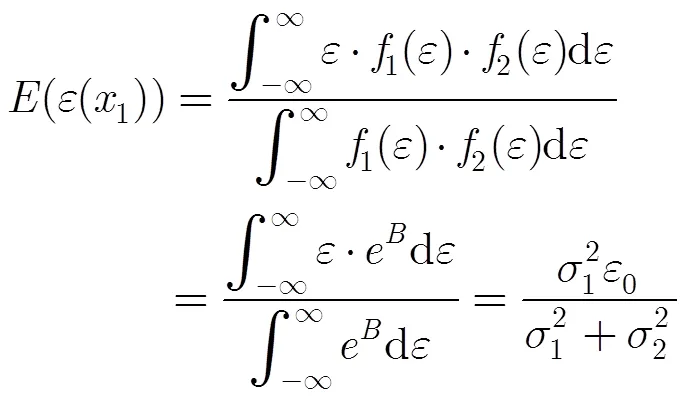
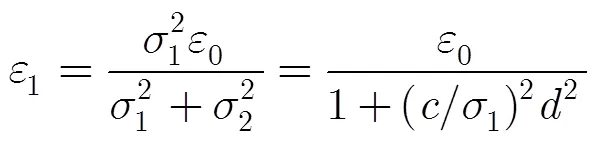
3.2 神经网络算法实现

只有一个硬点时，获取综合神经网络的算法步骤如下：

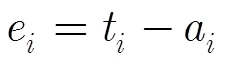
对于软点，输入/目标对的误差改为如下：

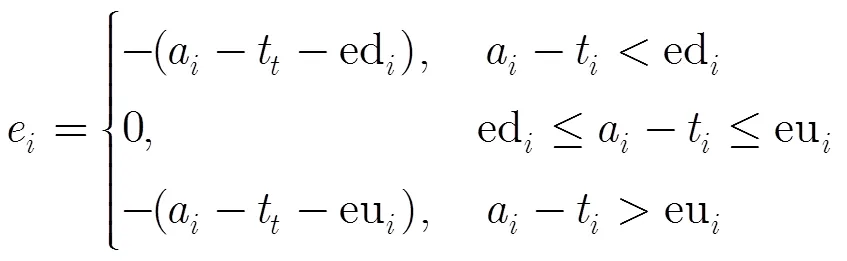
对于硬点，为使网络对硬点数据有更好的拟合，将硬点同时纳入到训练集、验证集和测试集中，且借鉴信息融合时常用的加权思想[17]，将硬点的输入/目标对误差进行放大：

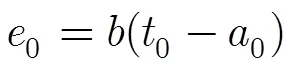
为硬点误差敏感系数，可取一个较大的值；

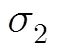
3.3 算例1

图1 含1个硬点和多个软点的训练样本及先验网络

4 针对多硬点样本的拟合算法

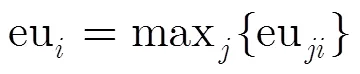
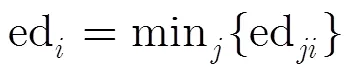
同理，对硬点误差进行放大

式(21)中，为硬点误差敏感系数。算法的实现过程与本文3.2节相同。以下两个算例将说明此算法对多硬点样本的拟合效果。

4.1 算例2

4.2 算例3

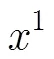
5 结束语

本文针对包含大量低置信级样本(实验样本)和少量高置信级样本(真实样本)的神经网络训练问题，提出涵盖所有已知信息下模型的期望(())的神经网络近似neth()，是代理真实模型()的最佳网络。通过对样本间误差关系的分析，提出此网络应等于先验网络与实验误差期望之和。引入了参数对实验误差的散布程度进行约束，通过计算软点误差容量区间[ed,eu]和引入硬点误差敏感系数，对标准神经网络训练过程中输入/目标对的误差进行了修改替换，多种情形下的算例证明，此方法在精确拟合高置信级样本的同时，尽可能地利用了低置信级样本的信息。与KBNN相比，该方法更加简单，可操控性更强并具有更加明确的逻辑意义。本文算法可用于神经网络的离在线结合训练，或系统变异后的重新学习。本文所做改进仅限于拟合问题，分类问题需要进一步研究。

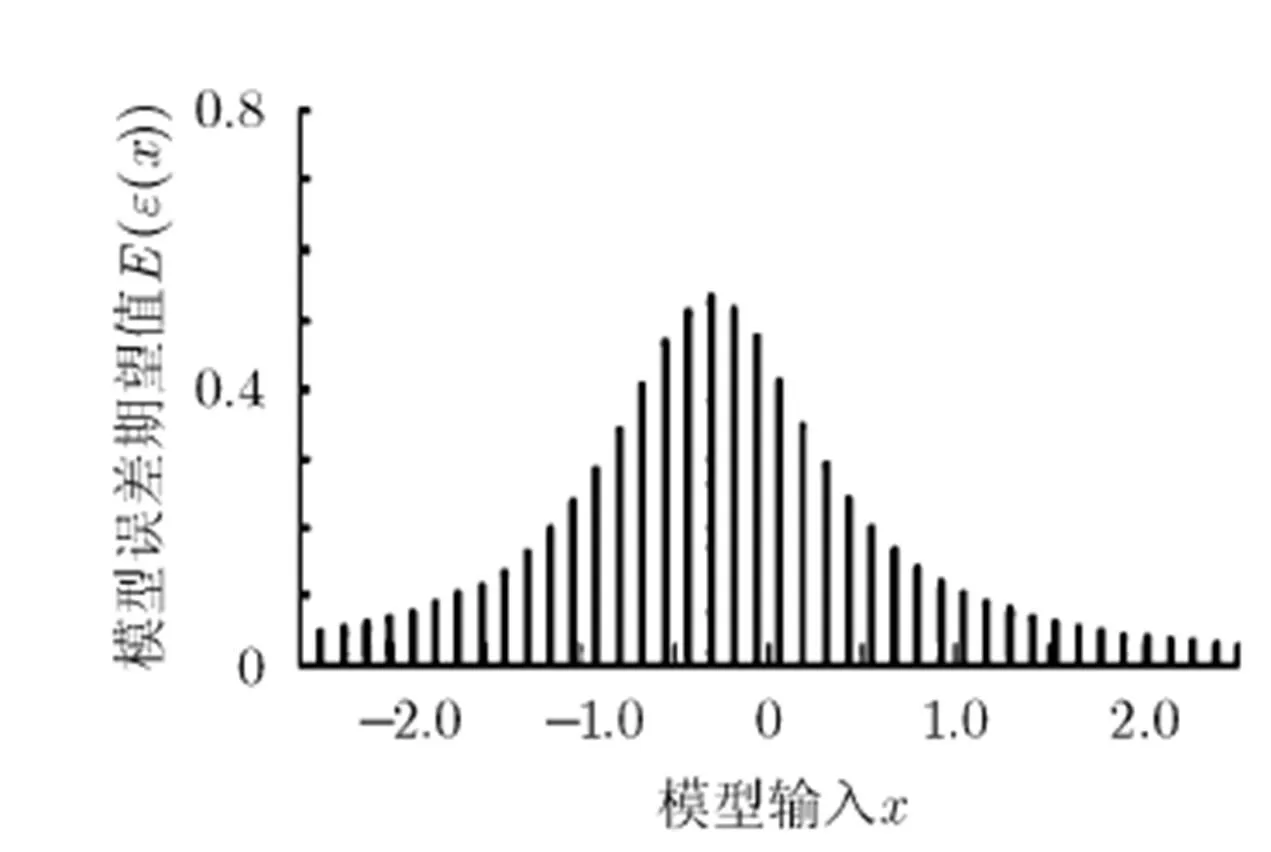
图2 r=2时的误差容量区间[ed,eu]

图3 取r=2时由本文算法获得的综合网络neth与先验网络nets对比

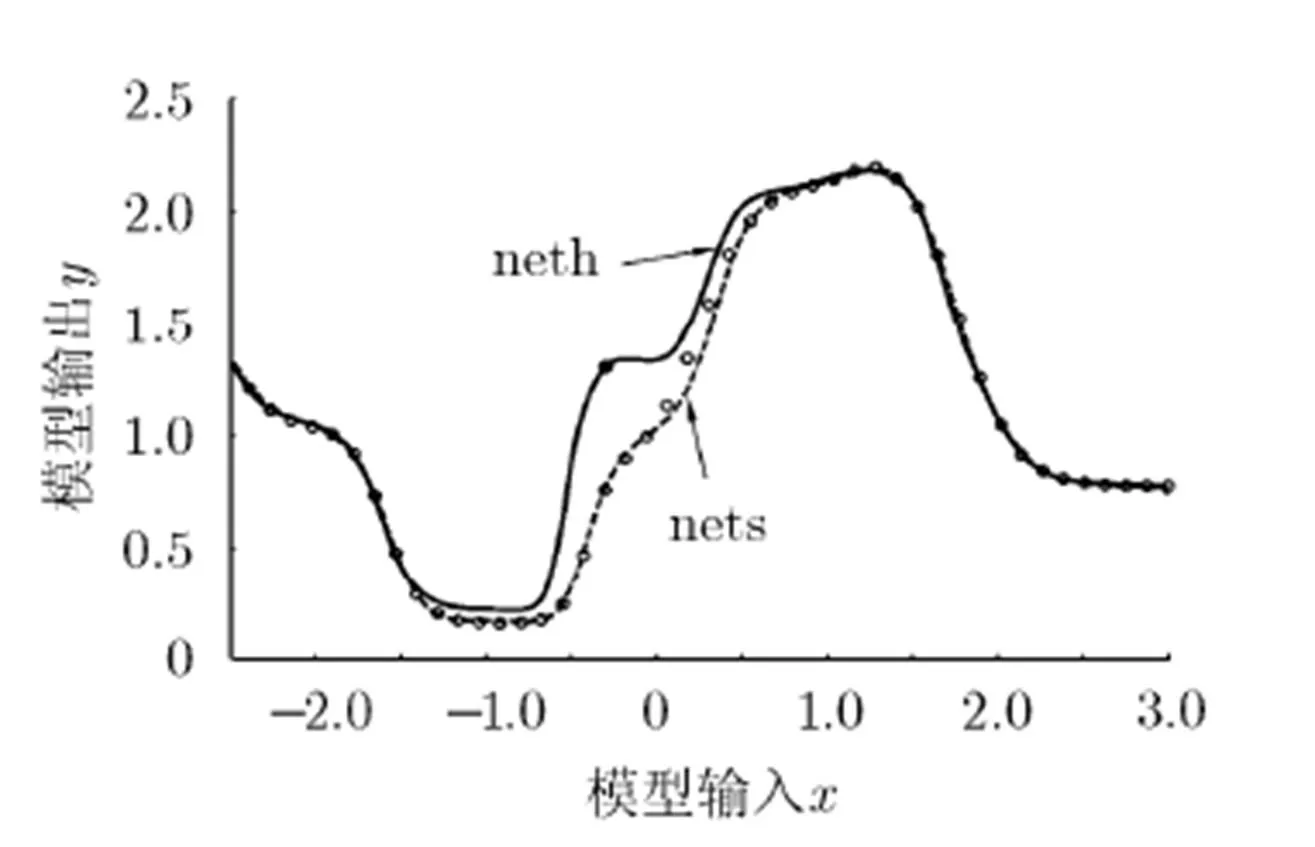
图4 取r=1.5时由本文算法获得的综合网络neth与先验网络nets对比

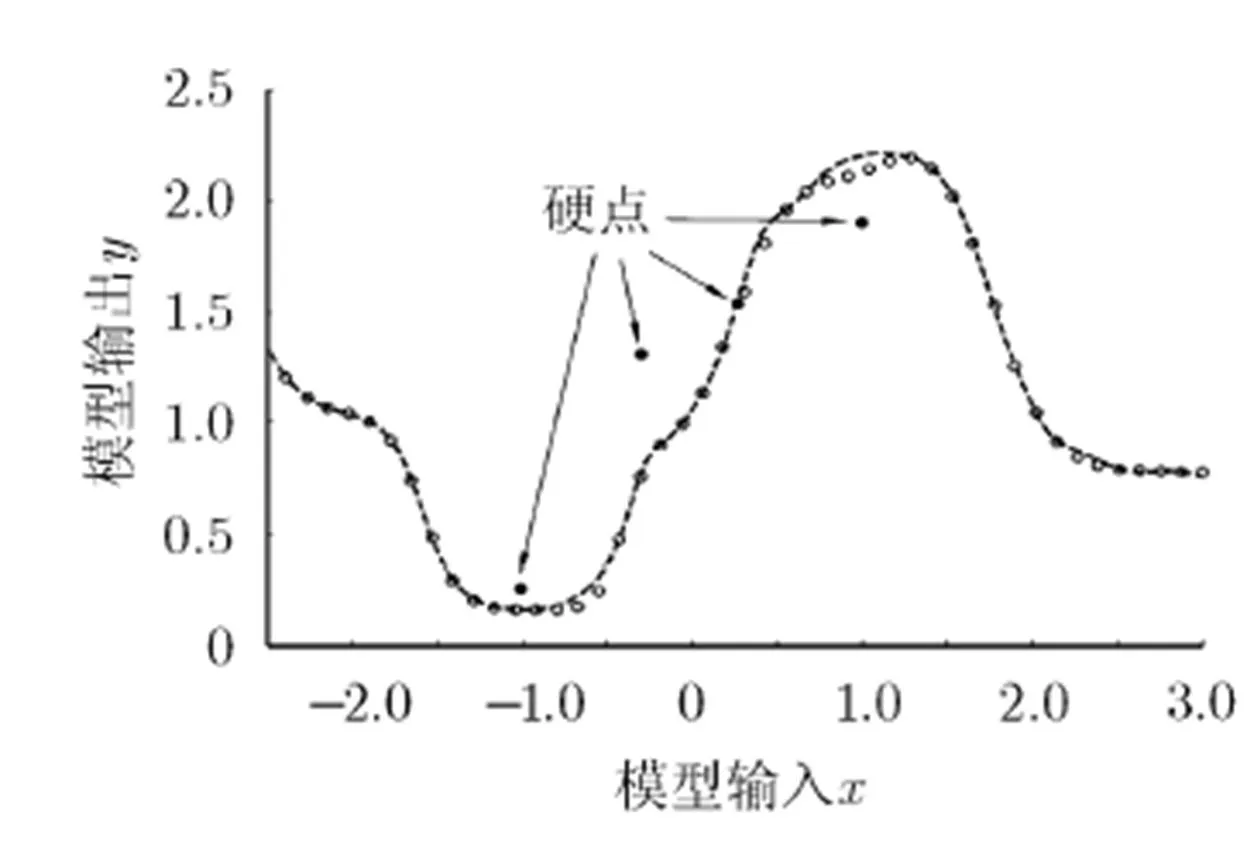
图5 含4个硬点和多个软点的训练样本及先验网络

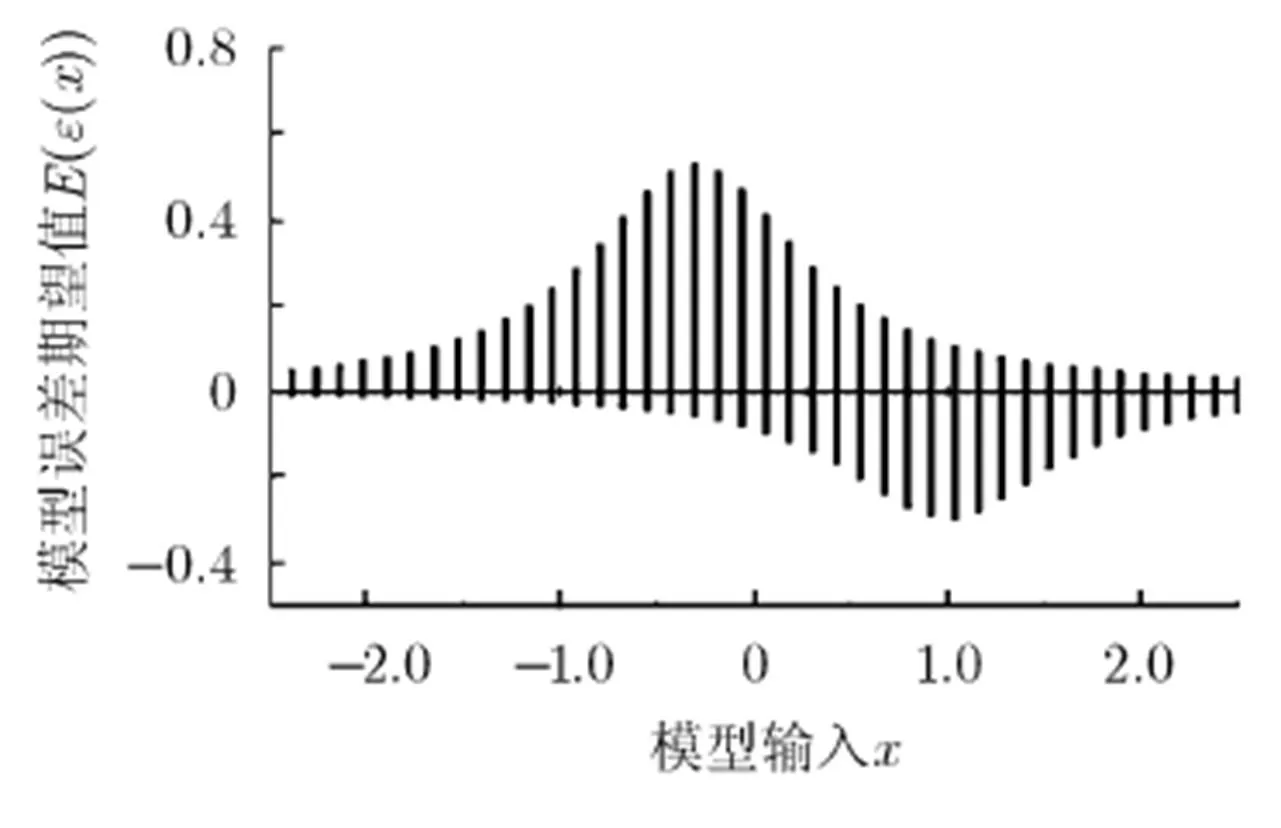
图6 r=2时的误差容量区间[ed,eu]

图7 本文算法获得的综合网络neth与先验网络nets对比

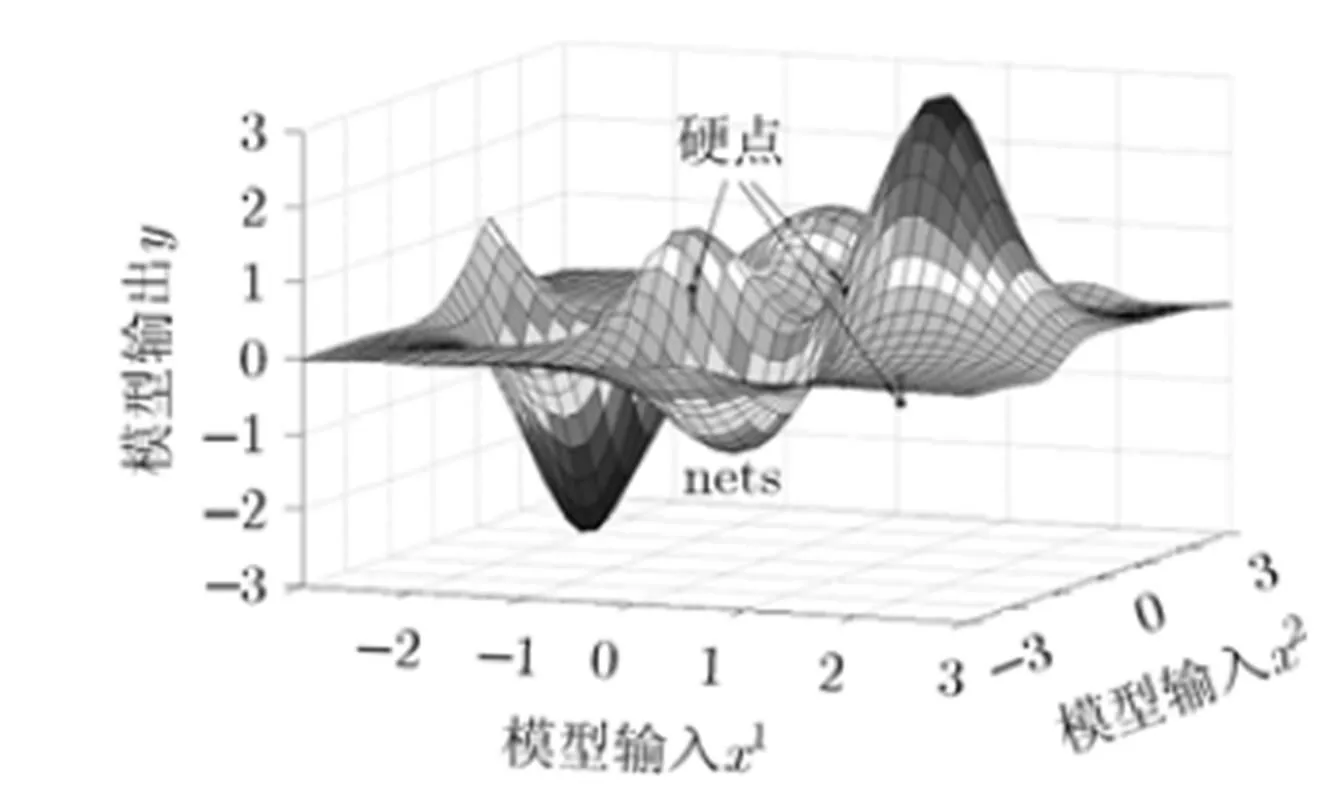
图8 含3个硬点的2维输入样本及先验网络

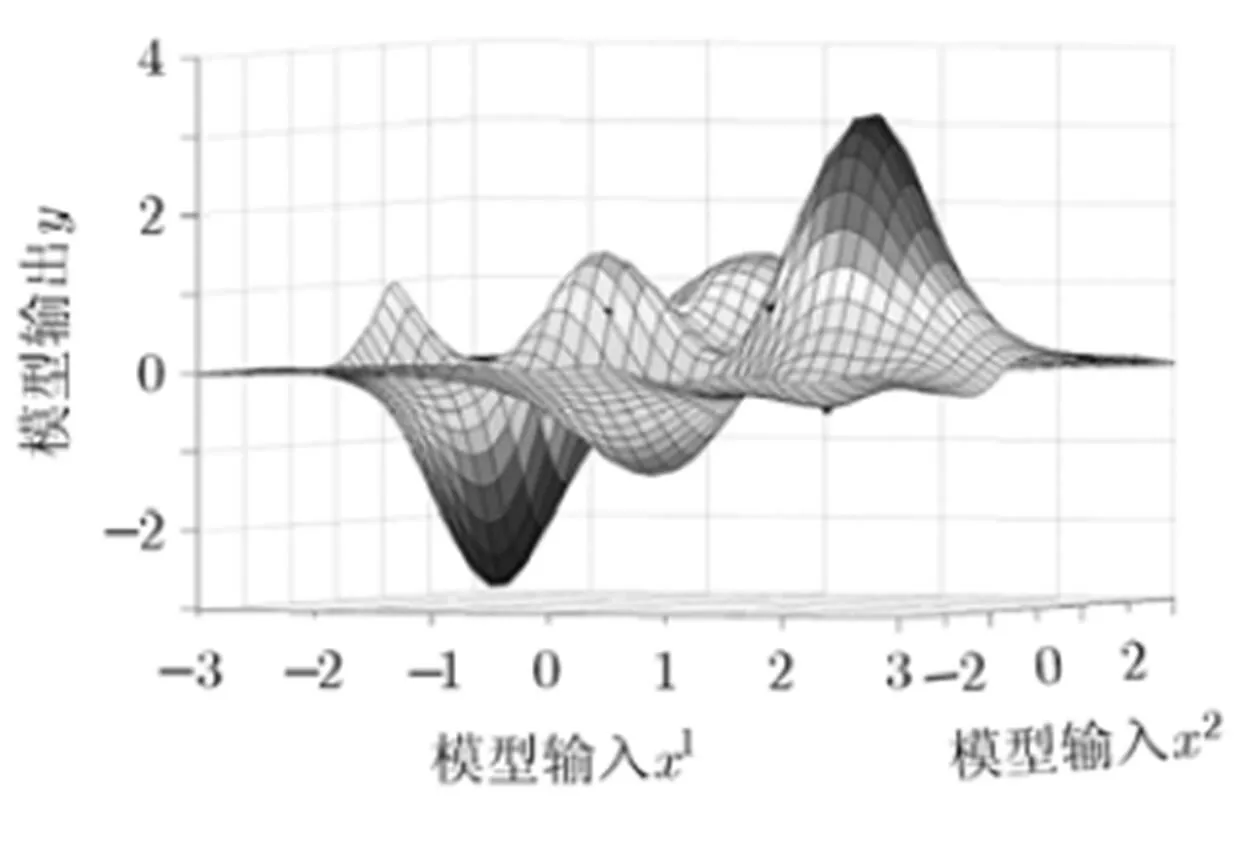
图9 本文算法获得的综合网络

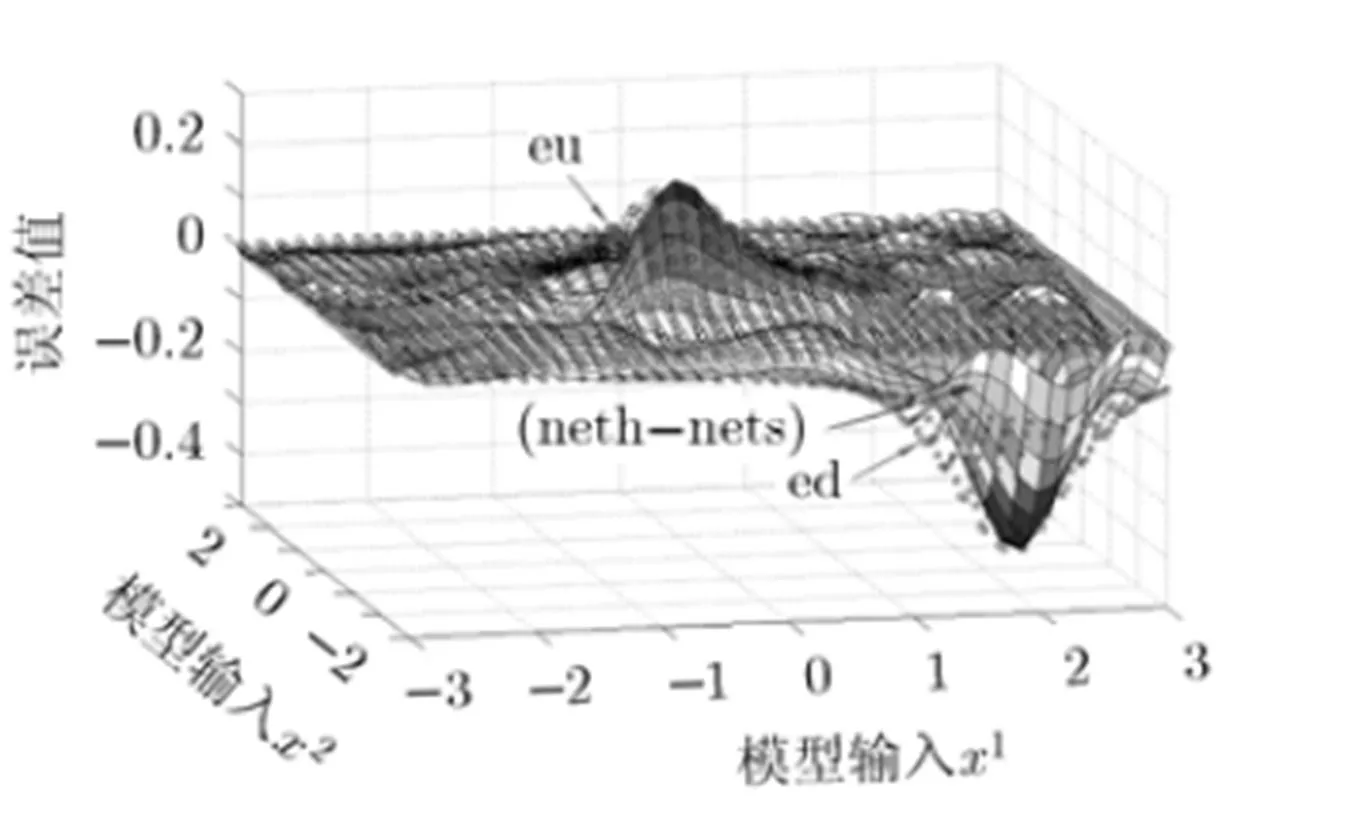
图10 综合网络与先验网络差值neth-nets及eu, ed

[1] Mitchell T M. Machine Learning[M]. New York: McGraw Hill Higher Education, 1997: 17.

[2] 李露, 李斌, 杜艳玲, 等. 样本量对飞灰含碳量的神经网络预测精度的影响[J]. 电力与科技工程, 2012, 28(9): 38-41.

[3] Milanic S, Strmcnik S, Sel D,.. Incorporating prior knowledge into artificial neural networks-an industrial case study[J]., 2004, 62(1): 131-151.

[4] Towell G G, Shavlik J W, and Noordewier M O. Refinement of approximate domain theories by knowledge-based neural networks[C]. Proceedings of the Association for the Advancement of Artificial Intelligence, Boston, 1990: 861-866.

[5] Sahin S, Tolun M R, and Hassanpour R. Hybrid expert systems: a survey of current approaches and applications[J]., 2012, 39(4): 4609-4617.

[6] Simsek M, Zhang Q J, Kabir H,.. The recent developments in knowledge based neural modeling[J]., 2012, 1(1): 1321-1330.

[7] 娄海川, 苏宏业, 谢磊. 融合过程先验知识的递归神经网络模型及应用[J]. 化工学报, 2013, 64(5): 1665-1673.

[8] 文刚. 用于步进电机细分控制的知识人工神经网络[J]. 现代电子技术, 2011, 34(7): 190-192.

[9] Yu Jian-bo, Xi Li-feng, and Zhou Xiao-jun. Intelligent monitoring and diagnosis of manufacturing processes using an integrated approach of KBANN and GA[J]., 2008, 59(5): 489-501.

[10] Serpen G, Tekkedil D K, and Orra M. A knowledge-based artificial neural network classifier for pulmonary embolism diagnosis[J]., 2008, 38(2): 204-220.

[11] Akkala A, Bhatt D, Devabhaktuni V,Knowledge- based neural network appoaches for modeling and estimating radon concentrations[J].&, 2013, 32(2): 355-364.

[12] 鲜于建川, 隽志才. 基于知识的神经网络在出行方式选择中的应用研究[J]. 计算机应用研究, 2008, 25(9): 2651-2654.

[13] Gajzler M. The idea of knowledge supplementation and explanation using neural networks to support decisions in construction engineering[J]., 2013, 57: 302-309.

[14] Iqbal R A. Empirical learning aided by weak domain knowledge in the form of feature importance[C]. 2011 International Conference on Multimedia and Signal Processing, Guilin, 2011: 126-130.

[15] Yoon H, Park C S, Kim J S,Algorithm learning based neural network integrating feature selection and classification[J]., 2013, 40(1): 231-241.

[16] Jones J K, and Goel A K. Perceptually grounded self- diagnosis and self-repair of domain knowledge[J].-, 2012, 27: 281-301.

[17] 朱永生, 王成栋, 张优云. 基于证据加权调整方法的神经网络及其在故障诊断中的应用[J]. 机械工程学报, 2002, 38(6): 66-71.

高学星： 男，1987年生，博士生，研究方向为参数不确定性与故障诊断.

孙华刚： 男，1979年生，高级工程师，研究方向为机械系统故障诊断.

侯保林： 男，1965年生，教授，博士生导师，研究方向为火炮自动供输弹系统.

A Neural Network Learning Method Using Sampleswith Different Confidence Levels

Gao Xue-xing①Sun Hua-gang②Hou Bao-lin①

①(,,210094,)②(,050000,)

To solve the model-fitting problem with different confidence levels of samples, a Neural-Network (NN)- based twice learning method is proposed. It is pointed out that the real model is a variation of experimental model. The neural network approximation to the mathematical expectation of real model, is believed to be the best network fusing the information of prior samples and real samples. In the first learning, neural network is trained using the prior samples only, and the error capacity intervals of the soft points, which are determined by the information of hard points, are calculated. Then, both prior samples and real samples are included in the training samples. The import-objective errors in the process of NN training are modified, using soft point error capacity intervals and hard point error-sensitivity coefficients. The expected network is generated by the second learning, with accurate fitting to the real samples and efficacious utilization of the prior samples. In contrast with Knowledge-Based Neural Networks (KBNN), this method is simpler and more amenable to manipulation with definite logical significance.

Neural Networks (NN); Model-fitting; Knowledge-Based Neural Networks (KBNN); Prior knowledge

TP183

A

1009-5896(2014)06-1307-05

10.3724/SP.J.1146.2013.01099

高学星 hss1737@gmail.com

2013-07-25收到，2013-12-09改回

国家自然科学基金(51175266/E050604)资助课题