常利率复合二项风险模型的破产概率分布

乔克林，乔小宁，曹振江

(延安大学 数学与计算机科学学院，陕西 延安 716000)

经典风险模型及其推广模型的重要结果为保险公司稳定经营奠定了坚实的理论基础，但随着金融市场的不断繁荣和发展，出现了保险公司在同一保险事故发生时可能面临多个风险的情况，并且保险公司的大部分盈余来自于投资收入，所以讨论有固定利率的多险种风险模型更能与保险公司的实际运作相符合。由于带利率的风险模型难度比较大，因此目前对这类问题的研究还不够深入。当理赔和保单的到达次数是一个Poisson过程的情形，文献［1－5］中有比较系统的研究，主要使用更新方程和鞅的方法。但对于理赔和保单的到达次数是二项过程的情况研究较少。为了使得风险理论研究内容和结果更加丰富多彩、更具有使用价值本文将对常利率下的复合二项双险种模型的破产概率做进一步的研究。

1 模型引入

以下所涉及的随机过程和随机变量都定义在同一个完备的概率空间(Ω，F，P)上，考虑模型

假设:

3)当理赔发生时，以下三种理赔有且仅有一种可能发生:(1)只发生第一种险种的索赔:(2)只发生第二种险种的索赔:(3)两种索赔都发生。

以上三种事件发生的概率分别为P1，P2，P3，显然P1+P2+P3=1。

设第一种险种的索赔额Z1，服从分布函数H1(z)，均值为μ1;第二种险种的索赔额Z2，服从分布函数H2(z)，均值为μ2;则第三种事件的索赔额应服从分布函数H1*H2(z)，均值为 μ1+μ2，且Z1，Z2是相互独立的。设Dj=Z1jδ1+Z2jδ2+(Z1j+Z2j)δ3为保险的第j次的理赔额，其中δk为0－1随机变量，当δk=1时，表示第k种事件发生，而且对于每次索赔，有且仅有一个δk=1，它发生的概率为Pr(δk=1)=pk，k=1，2，3。Zij表示第i种险种在第j次索赔时的索赔额，且它们相互独立，i=1，2。用D表示任意的Dj，由全概率公式可知D的分布函数为H(D)=p1H1(D)+p2H2(D)+p3H1*H2(D)，则

E［D］= μD=p1μ1+p2μ2+p3(μ1+ μ2);

5)存在r∞＞0，使得当r→r∞时，有

模型的实际背景:在保险公司的事务中，假定只在离散时间n进行至多一次赔付并且收取保费，在连续时间段(n－1，n］中进行的赔付以及收取的保费均视为在时刻n进行的。并且在时刻n=0时保险公司有初始资本u。

由于破产只可能发生在理赔时刻，记为:

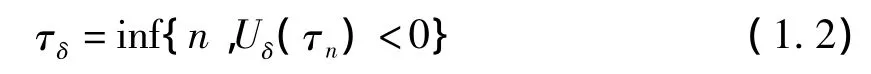
则τδ为模型(1.1)的破产时刻;若将保险公司在第n次理赔或之前破产的概率记为:

则模型(1.1)在初始资本u下的破产概率为φδ(u)=P(T＜ ∞ |Uδ(0)=u);Ψδ(u)为模型(1.1)在初始资金为u下的生存概率，则有

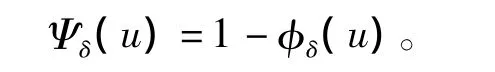
2 主要结果

引理［6］对所有0 ＜S＜t，及整数m，n(m＜n)，用@表示分布相同，有

其中U(i)表示［0，t－s］上n－m个均匀分布的独立随机变量U1，U2，L，Un－m的第i个次序统计量，特别地，若令s=0，m=0，有

定理2.1 保险公司第n+1次赔付破产或之前破产概率为

证明 假设第一次索赔导致破产，由定义可得

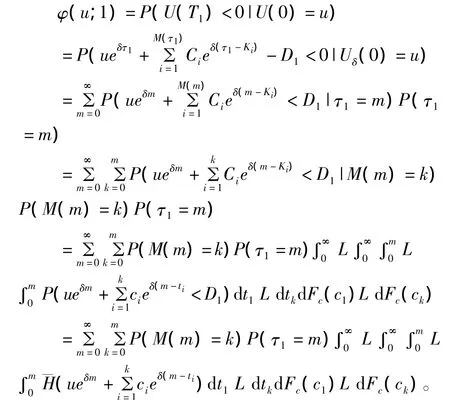
假设第n+1次索赔或之前导致破产，由定义可得

推论2.1 保险公司的破产概率为

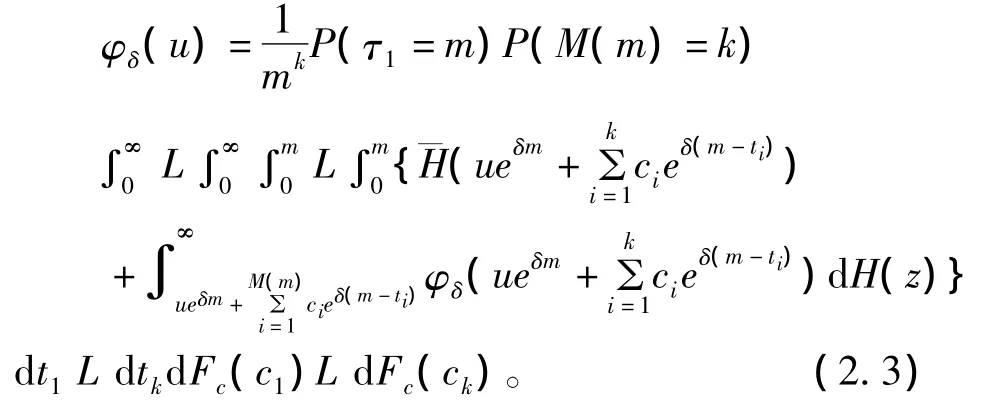
证明:定理2.1中的n→∞时即证。

推论2.2 保险公司的生存概率为

且Ψδ(u)满足如下积分方程:

证明 显然(2.4)式成立;下证(2.5)式成立，由推论2.1及(2.4)式有

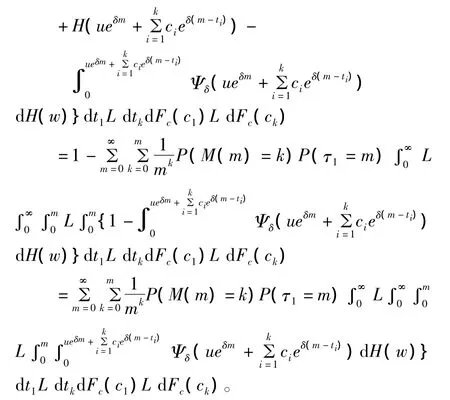
综上所述，保险公司的生存概率满足上述积分方程式(2.5)。证毕。

［1］乔克林，李粉香.带利率的特殊双险种风险模型的破产概率［J］.经济数学，2009，26(4):824－828.

［2］乔克林，李萍.一类双复合模型的破产概率的初步研究［J］. 延安大学学报:自然科学版，2011，23(4):40 －42.

［3］乔克林，侯致武，廖金林.常利率下特殊双险种风险模型的破产问题［J］.湘潭大学自然科学学报，2011，33(3):23－26.

［4］乔克林，侯致武.一类随机保费下带利率的双险种风险模型的破产问题［J］.河南科学，2011，29(9):1013－1016.

［5］乔克林，刘凤凤.一类相依风险模型破产概率上界的数值分析布［J］.科学技术与工程，2012，12(32):1671－1875.

［6］刘莉，茆诗松.常利率下风险模型破产问题的研究［D］.华东师范大学博士学位论文，2004.

［7］GerberH.U.数学风险论导论［M］(成世学，严颖译).北京:世界图书出版公司，1997.

［8］Garbled J．Aspects of risk theory［M］．Springer．Berlin．1991．

［9］刘莉，茆诗松.常利率下风险模型破产问题的研究［D］.华东师范大学博士学位论文，2004.

［10］唐国强，带息双二项风险模型的破产问题［J］.经济数学，2006，23(3):235 －242.

［11］黄玉娟，余文广，刘红梅 .Proceedings of International Conferenceon Engineering and Business Management(EBM2010).