一类三次系统极限环的存在唯一性
2014-05-30卜令杰窦霁虹刘萌萌
卜令杰,窦霁虹,刘萌萌,邢 伟
(西北大学 数学系,陕西 西安 710127)
之内。如果
(5)当f1(x)≡0时,系统(1)可写成:
单调递增且f(0)=δ<0,
(x1,x2)上 f1(x)>0,在(
随着多项式系统相伴系统的引入,对具有不变直线的多项式系统的定性研究越来越受到人们的关注。在什么条件下一对相伴系统的中心焦点问题,极限环的个数等问题上是一致的或是不一致的,这些问题复杂而有趣,它的研究将大大丰富多项式系统定性研究的内容和方法[1-9]。
本文研究的三次微分系统:
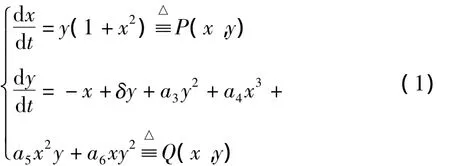
(其中 δ,a3,a5,a6均为实常数,a4>0)是周久红硕士学位论文中第三个系统的具有二虚不变直线的相伴系统。通过对系统进行了定性分析,得到了该系统极限环存在性、唯一性的若干充分条件。并将两系统极限环存在性、唯一性的若干充分条件作了比较。
1 平衡点的性态
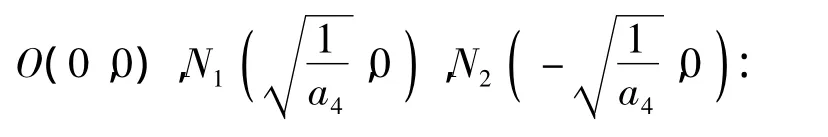
(i)当-∞ <δ≤-2时,O是系统(1)的稳定的结点,N1,N2是系统(1)的鞍点;
(ii)当-2<δ<0时,O是系统(1)的稳定的粗焦点,N1,N2是系统(1)的鞍点;
(iii)当0<δ<2时,O是系统(1)的不稳定的粗焦点,N1,N2是系统(1)的鞍点;
(iv)当2≤δ<+∞时,O是系统(1)的不稳定的结点,N1,N2是系统(1)的鞍点。
证明:系统(1)在奇点O处的线性变分矩阵为:
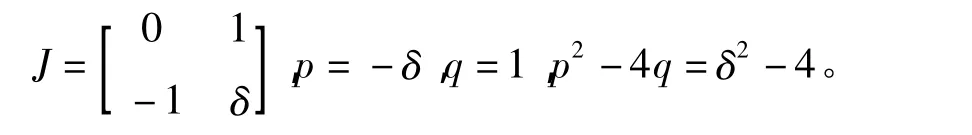
故得以下结论:
(i)当-∞ <δ≤-2时,O是系统(1)的稳定的结点;
(ii)当-2<δ<0时,O是系统(1)的稳定的粗焦点;
(iii)当0<δ<2时,O是系统(1)的不稳定的粗焦点;
(iv)当2≤δ<+∞时,O是系统(1)的不稳定的结点。
系统(1)在奇点N1,N2处的线性变分矩阵均为:
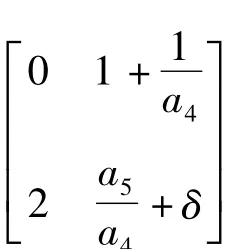
定理2 对于系统(1),当δ=0时,有:
(i)当a5>0时,奇点O是系统(1)的一阶不稳定的细焦点;
(ii)当a5<0时,奇点O是系统(1)的一阶稳定的细焦点;
(iii)当a5=0时,奇点O是系统(1)的中心。
证明:当δ=0时,
令
F(x,y)=x2+y2+F3(x,y)+F4(x,y)+ …,其中Fj(x,y)是x与y的j次齐次多项式(j=3,4,…),则有:
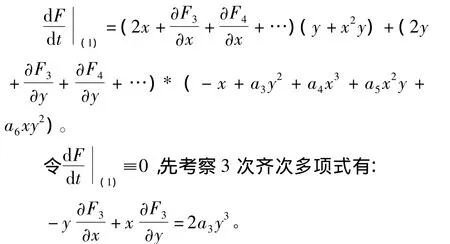
将上式取极坐标x=rcosθ,y=rsinθ,并消去r3后可得:

将上式取极坐标x=rcosθ,y=rsinθ,并消去r4后可得:

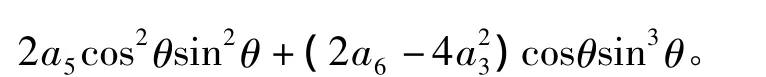
自然地,可以得到如下结论:
(A)当a5≠0时,
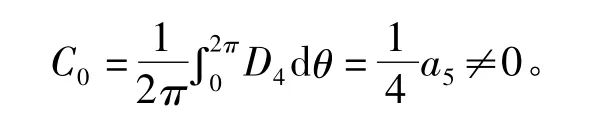
于是,改写F4使得:
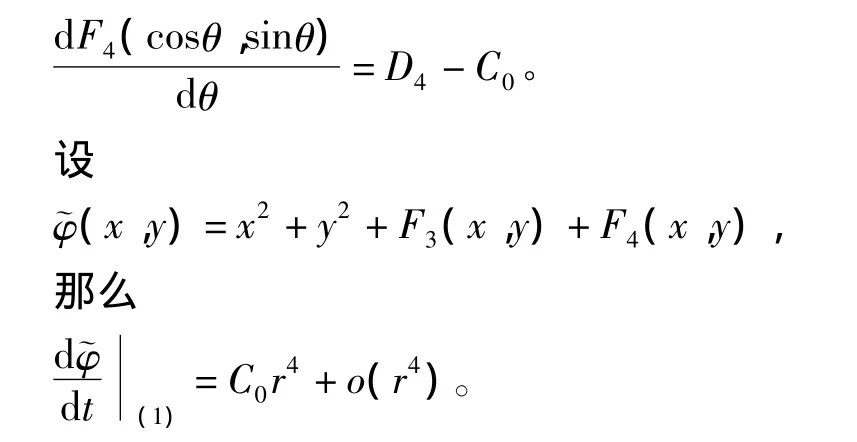
进而有结论:
(a)当a5>0时,奇点O是系统(1)的一阶不稳定的细焦点;
(b)当a5<0时,奇点O是系统(1)的一阶稳定的细焦点;
(B)当a5=0时,
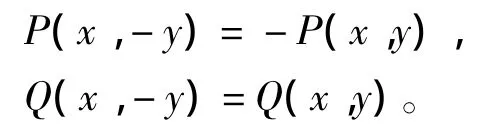
故由对称原理可知:当δ=0且a5=0时,奇点O是系统(1)的中心。
2 极限环的存在性、唯一性
定理3 下列条件之一成立时,系统(1)在全平面上不存在极限环。
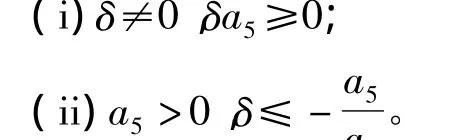

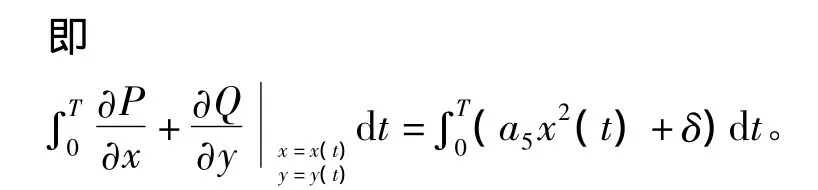
由此可知:
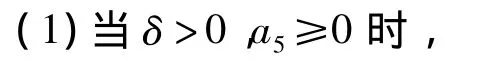
当 δ<0,a5≤0 时,
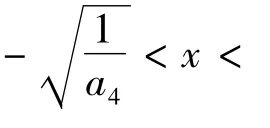
之内。如果
定理4 当a5=0,δ=0时,系统(1)在全平面上不存在极限环。
证明:由有限远奇点的性态分析可知,当a5=0且δ=0时,奇点O是系统(1)的中心而奇点N1,N2是系统(1)的鞍点,即该结论成立。
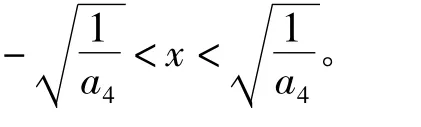
定理6 下列条件之一成立时,系统(1)在奇点O外围至少存在一个极限环,且当δ<0时所产生的极限环不稳定,当δ>0时所产生的极限环稳定。
(i)-1≪δ<5,a5>0,
(ii)0 <δ≪1,a5<0。
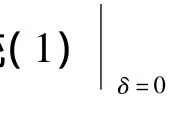
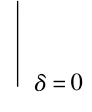
引理 1[10]形如
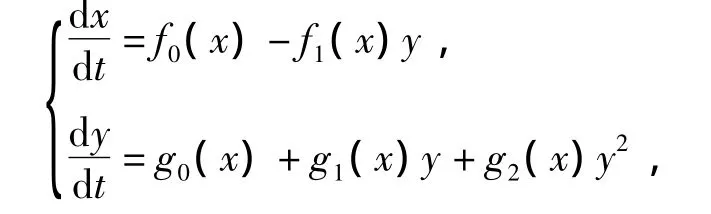
(其中f1(x)≠0)的方程都可以经过变量代换化为Lienard型方程:
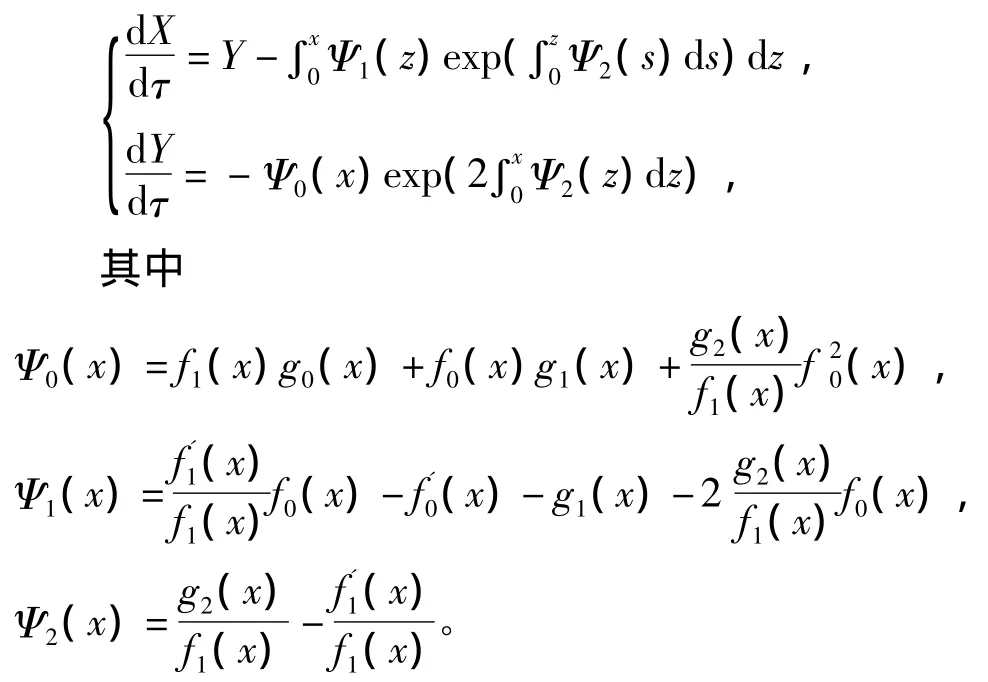
引理2[10]考虑微分方程组
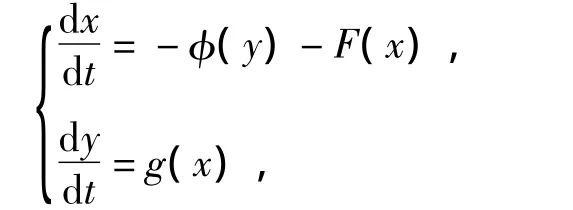
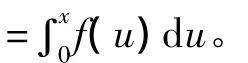
(1)当x≠0时,xg(x)>0;当y≠0时,yφ(y)>0。
(2)f(x),g(x),φ(y)连续可微;φ(y)单调递增;f(0)<0(f(0)>0)。
(3)存在常数 α,β,使f1(x)=f(x)+g(x)[α +βF(x)]有简单零点x1<0与x2>0,而且在区间(x1,x2)上f1(x)≤0(f1(x)≥0)。
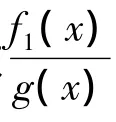
(5)所有闭轨线包围x轴上的区间[x1,x2]
则该系统最多有一个极限环;如果它存在,则是稳定的(不稳定的)。
定理7 下列条件之一成立时,系统(1)在奇点O外围至多存在一个极限环,且当δ<0时,若存在极限环则不稳定;当δ>0时,若存在极限环则稳定。
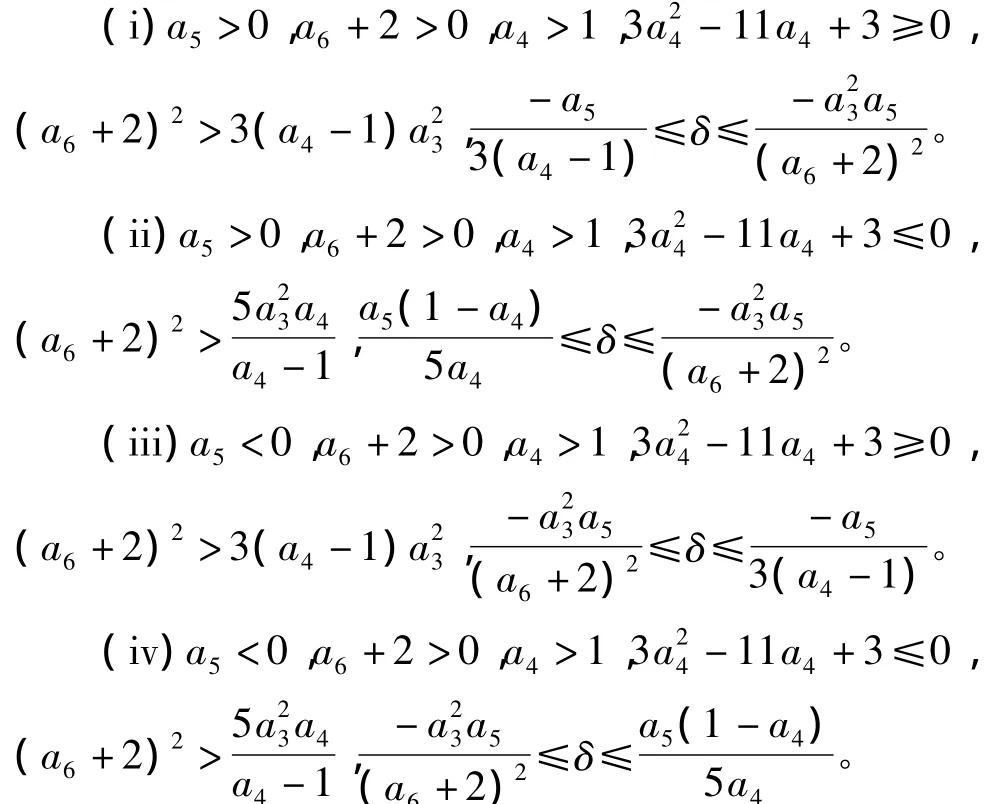
证明:由引理1可将系统(1)化为(仍以变量x,y记之):
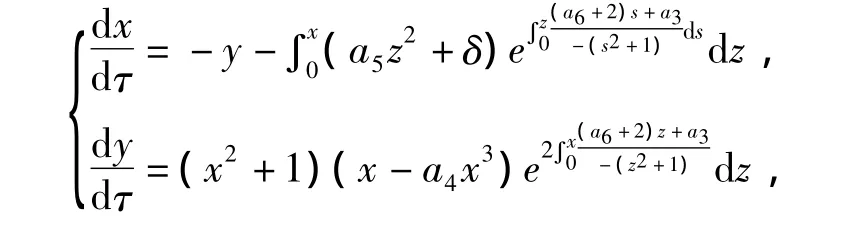
其中所作的时间变换为:
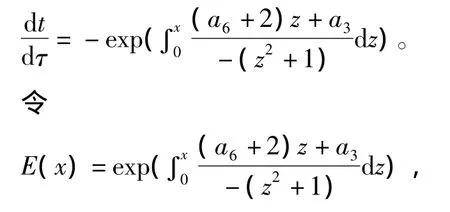
则由引理2知:
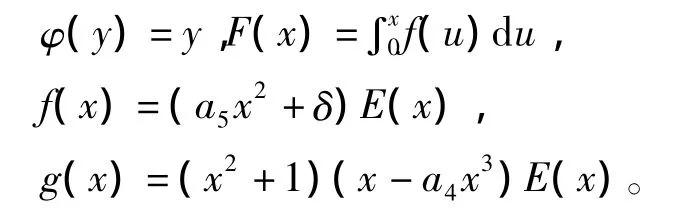

φ(y)=y单调递增且yφ(y)=y2>0,当y≠0时。
(4)f(x),g(x),φ(y)连续可微;f(0)= -δ。
(5)存在常数α=0,β=0使得f1(x)=f(x)+g(x)[0+0·F(x)]=(a5x2+δ)E(x)。
当a5与δ异号时,f1(x)有简单零点:x1=-
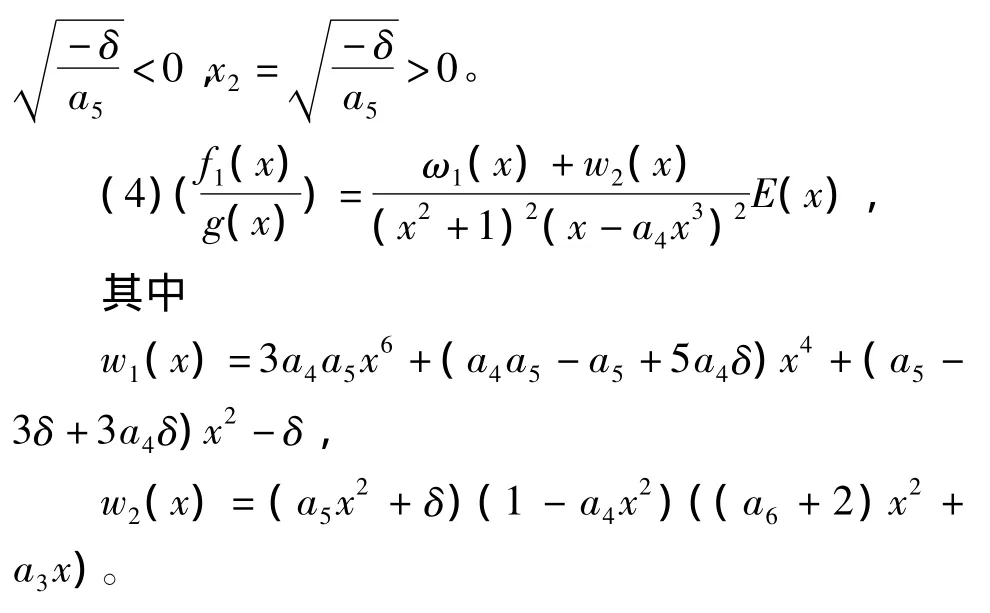
(5)当f1(x)≡0时,系统(1)可写成:
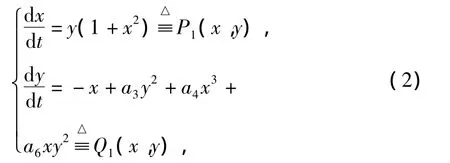
易知:

则当x∈(x1,x2)时,PQ1-P1Q定号。根据比较原理,当x∈(x1,x2)时,系统(1)的闭轨线与系统(2)的闭轨线必重合或不相交。显然,系统(1)的闭轨线与系统(2)的闭轨线不重合,从而在带域x1<x<x2中,系统(1)与系统(2)的闭轨不能相交。当f1(x)≡0时,奇点O(0,0)是系统(2)的中心,所以系统(2)的闭轨将充满带域x1<x<x2。如果系统(1)的闭轨不完全包含区间(x1,x2),则系统(1)经过区间(x1,x2)上任一点的闭轨必与系统(2)的闭轨相交,这与在带域x1<x<x2中,系统(1)与系统(2)的闭轨不能相交相矛盾。所以系统(1)的闭轨如果存在则必包含定理相应条件下的区间(x1,x2)。
通过上面的分析知:

单调递增且f(0)=δ<0,
(x1,x2)上f1(x)>0,在(
由定理6与定理7易得:
定理8 下列条件之一成立时,系统(1)在奇点O外围存在唯一极限环,且当δ<0时极限环不稳定,δ>0时极限环稳定。
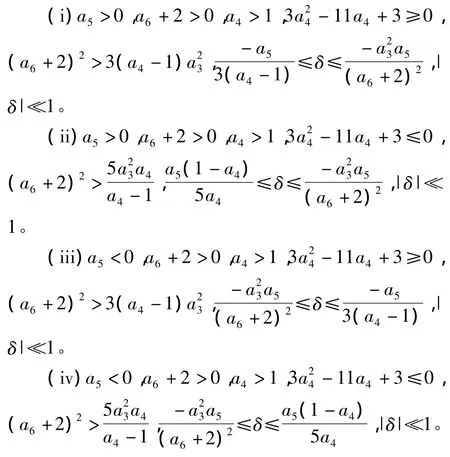
3 结论
由周久红的硕士学位论文[8]和本文的结果可知:系统(1)与周久红的硕士学位论文中的第三个系统相比,其奇点的性态相同,且无极限环、至少存在一个极限环的充分条件相同,但至多存在一个极限环、存在唯一极限环的充分条件发生了变化。
[1]李建全,马知恩.一类三次系统极限环的存在唯一性[J].系统科学与数学,1999,19(1):16 -18.
[2]梁锦鹏.一类三次系统的极限环Ⅱ[J].系统科学与数学,2008,28(5):576 -587.
[3]方成鸿.一类三次系统极限环的存在性与唯一性[J].宁德师专学报(自然科学版),2011,23(2):122-125.
[4]张瑞海,陈海波.一类平面三次微分系统极限环的存在性与唯一性[J].数学理论与应用,2004,24(3):32-35.
[5]石志高,吴承强.一类三次微分系统极限环的存在性和唯一性[J].福州大学学报(自然科学版),2007,35(3):344-347.
[6]刘兴国,刘斌,吕勇.一类平面三次系统极限环的存在唯一想[J]. 湖南工业大学学报,2010,4(1).
[7]谢向东,张建峰.平面多项式系统及相伴系统[J].数学研究,2004,37(2):161 -166.
[8]周久红.一类三次系统的定性分析[D].研究生硕士论文 .2013,4.
[9]Han Yu - liang.A class of cubic systems with a ninth order singular point[J].Ann of Diff Eqs,1991,7(1):13 - 24.
[10]叶彦谦.极限环论[M].上海:上海科学技术出版社.1984.
