高速铁路列车振动荷载对下穿隧道地层动力响应分析

高玄涛

(中铁第一勘察设计院集团有限公司，西安 710043)

近年来，我国轨道交通得到大力发展。随着我国轨道交通的大规模建设，近接工程数量越来越多，施工难度也越来越大。特别是隧道下穿高速铁路施工时，不可避免地对周围土体产生扰动，引起周围地层损失及路基沉降，造成高速铁路轨道的纵、横向不平顺，从而影响列车的运营安全［1］。以某隧道下穿高速铁路项目为研究背景，主要采用数值模拟的方法对下穿隧道施工至不同位置时列车动载作用下地层动力响应进行研究分析，为下穿隧道施工提供理论指导。

1 工程概况

该隧道下穿高速铁路A(即将投入运营)、客运专线B(已运营)、客运专线C(在建)段，需与在建的工程同步完成施工。隧道全长300 m，隧道内为单面坡，隧道开挖拱顶到上部铁路轨顶面最大埋深约27.3 m。隧道下穿段与地表高速铁路A、客运专线B及客运专线C在平面位置上呈斜交，斜交角度约30°。

高速铁路A本段地基采用CFG桩加固，桩径0.5 m，桩长 10.5 m，桩底高程约 13.275 m，桩端一般进入强风化层不少于0.5 m，桩间距1.80 m，按正方形布置，桩顶设1.0 m扩大桩头，桩顶设0.6 m厚垫层(0.2 m厚中粗砂+0.4 m厚碎石)，垫层内铺设二层双向经编高强土工格栅;土工格栅极限抗拉强度不小于100 kN/m。地基表层挖除换填0.5 m厚C组填料后再打桩。

客运专线B本段地基采用CFG桩加固，桩径0.5 m，桩长9.5～6.5 m，CFG 桩桩端进入硬层不少于1.0 m;桩间距 1.8 m，按正方形布置，桩顶设直径为1.0 m扩大桩头;桩顶设0.6 m厚垫层(0.2 m厚中粗砂+0.4 m厚碎石)，垫层内铺设二层双向经编高强土工格栅;土工格栅极限抗拉强度不小于100 kN/m。地基表层挖除换填0.5 m厚C组填料后再打桩。

客运专线C本段地基采用CFG桩加固，桩径0.5 m，桩间距1.6 m，桩长 3.0 ～9.0 m(桩长嵌入全风化层内不小于1.0 m)，按正三角形布置。CFG桩桩顶采用1 mx1 m扩大桩头，桩顶设0.5 m厚碎石垫层，垫层内铺设1层双向经编土工格栅，土工格栅抗拉强度不小于250 kN/m。

下穿隧道与地表线路路基相对位置及纵断面分别见图1、图 2。

图1 工程平面位置(单位:m)

图2 工程纵断面(单位:m)

2 地质概况

隧道处地貌为秦淮河及其阶地、岗地、坳谷以及剥蚀丘陵，隧道洞身位于第四系地层中。根据地质资料揭露，上部为2～5 m厚人工填土，下部为第四系上更新统粉质黏土层，硬塑，厚度0～5 m，具有弱膨胀性，下伏基岩为白垩系砂岩或侏罗系凝灰岩、砂岩，节理裂隙发育，全风化～弱风化，地下水主要赋存于土层与风化层、强风化与弱风化层间及岩层裂隙内，水量较丰富。隧道拱顶以上0～3 m范围为弱风化岩，隧道所处地质根据围岩情况判定为Ⅲ～Ⅳ级，根据隧道穿越地段地表建筑物的重要性及地下水情况，将隧道按为Ⅴ级型式加强支护。如图3所示。

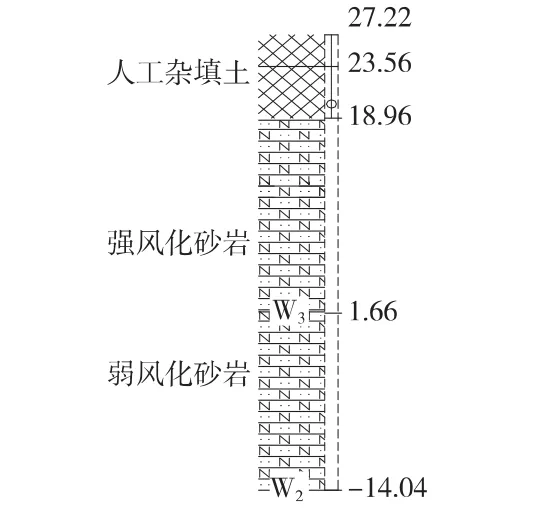
图3 地质柱状图(单位:m)

3 动力分析本构模型

土的动力本构关系是极其复杂的，它在不同的荷载条件、土性条件下会表现出极不相同的动力本构特性。目前具体建立的动力本构模型已达数十种，大致可以分为线弹性模型、黏弹性模型、弹塑性模型、边界面模型、内时模型等［2］。

根据弹塑性理论，土体变形可以分为弹性变形和塑性变形两部分，其中弹性变形可以应用广义胡克定理计算，塑性变形可以应用塑性增量理论计算。塑性增量理论包含3个基本要素:屈服准则、流动法则和硬化定律，分别规定了塑性应变增量的产生条件、方向和大小。目前基于不同的基本要素已经提出了多种弹塑性本构模型，如Drucker-Prager模型、多重屈服面模型(Nested Surfaces Model)、边界面模型(Bounding Surfaces Model)等［2］。

事实上，目前还没有一种本构模型能够模拟各种情况下土的动力非线性特征，并具有实际应用中必要的简单性。因此针对具体的问题应该选择合理而简单的本构模型［2］。

ABAQUS是国际上最先进的大型非线性有限元计算分析软件之一，具有强健的非线性计算功能。其提供的非线性模型有Mohr-Coulomb模型、扩展的Drucker-Prager模型、修正Drucker-Prager帽盖模型、(修正)剑桥模型。其中Mohr-Coulomb模型在岩土工程中应用最广泛，模拟结果与实际也较为吻合。因此计算中采用 Mohr-Coulomb 模型［3］。

4 有限元计算模型的建立

采用三维有限元模型进行计算。根据工程实际及圣维南原理，参考已有研究成果进行建模［4-7］，隧道顶部以上覆土为23.5 m，隧道底部以下为29.7 m，左右边界分别离隧道中线50 m，纵向延伸50 m。通过ABAQUS程序建立的计算分析模型如图4所示。

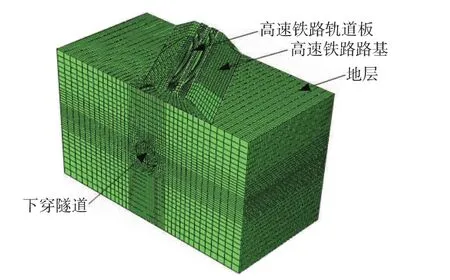
图4 下穿隧道计算分析模型

4.1 本构模型

土体的非线性本构模型:采用了弹塑性物理模型。衬砌单元采用强度等级为C35的钢筋混凝土，计算时采用Mohr-Coulomb本构模型并将混凝土与钢筋合为一体考虑。为了建模及划分网格方便，将计算区域不同地层简化为同一地层，土体参数进行相应转换。根据下穿隧道段地质勘察资料，计算过程中土体的材料参数取值如表1所示。

表1 材料物理力学参数

4.2 边界条件［8-10］

本工程通过对固定边界、黏性边界条件及无限元边界条件进行计算比较分析，计算结果相差不大，一方面是由于列车振动荷载不是很大，另一方面模型选取的比较大，列车振动荷载传至边界处时已衰减较多。而从计算所需时间上看，固定边界所需时间要少，故选用固定边界进行计算。

固定边界条件:土层底部完全固定;左右两侧面限制水平方向的位移，竖向自由;前后两面限制轴线方向的位移，竖向自由;地面完全自由。

5 动力计算及结果分析

本文针对无砟轨道的结构特点，采用弹性地基梁板模型分析了CRTSⅠ型板式无砟轨道结构动力响应，给出了CRTSⅠ型板式无砟轨道结构在CRH2型列车以时速350 km经过时轨下压力时程曲线，确定了列车振动过程中的激励荷载［11］。如图5所示。

图5 列车轮轨激振力时程曲线

本文主要计算了隧道开挖到不同位置时列车以时速350 km通过，研究地层动力响应。计算过程中分别在地层表面、地层不同深度处及隧道拱顶设置监测点，监测该处位移变化情况。

5.1 地层表面监测点位移分析

隧道分别开挖至15、25 m和35 m时，施加列车振动荷载，地层表面各监测点在列车动载作用下的竖向位移时程曲线如图6所示。

图6 隧道开挖至不同位置时施加动载地表监测点位移时程曲线

隧道开挖至不同位置施加动载地表监测点最大竖向位移如表2所示。

表2 地表监测点最大竖向位移 mm

通过对隧道开挖至不同部位施加动载地表监测点位移时程曲线及最大位移值分析可知。

(1)在单次列车动载作用下地表监测点产生的竖向位移值与隧道开挖引起的沉降量相比很小，可以忽略不计(隧道开挖引起的最大沉降量为2.7 mm)。但是根据国内外工程实际在长期高速列车振动荷载的作用下，地层产生的沉降量是不能忽视的;

(2)随着一组组车轮的滚过，监测点位移时程曲线具有明显的车轮滚过效应;当车轮压在监测点时，该监测点出现位移峰值，车轮离开监测点后，位移逐渐减小;当列车驶离后，位移逐渐回弹恢复;

(3)当第一节车厢经过时，z=15 m处监测点产生的位移最大;随后，z=25 m处即下穿隧道与高速铁路路基交叉点处监测点位移最大，因此，在设计与施工时要注意对下穿隧道与高速铁路路基交叉部分加强支护;

(4)隧道中点前监测点随着隧道开挖的不断进行，施加动载产生的位移值在逐渐减小;隧道中点及中点后监测点则随着隧道开挖的不断进行，施加动载产生的位移值在不断增大。

5.2 隧道拱顶监测点位移分析

隧道分别开挖至15、25 m和35 m时，施加列车振动荷载，隧道拱顶各监测点在列车动载作用下的竖向位移时程曲线如图7所示。

图7 隧道开挖至不同位置时施加动载隧道拱顶监测点位移时程曲线

隧道开挖至不同位置施加动载隧道拱顶监测点最大竖向位移值如表3所示。

表3 拱顶监测点最大位移值 mm

通过对隧道开挖至不同部位施加动载隧道拱顶监测点位移时程曲线及最大位移值分析可知:

(1)隧道拱顶位移时程曲线表现出和地表位移时程曲线同样的特性;

(2)隧道开挖至某一处施加动载，该处拱顶产生的位移值最大，因此，隧道开挖后，特别是上台阶开挖后，要及时施加支护;

(3)随着开挖的不断推进，开挖面即掌子面处拱顶位移值在不断增大。

5.3 地层不同深度监测点位移分析

为研究在列车动载作用下，地层不同深度处动力反应，取隧道开挖面即掌子面处地层不同深度监测点来进行研究，监测点布置如图8所示。隧道开挖至不同位置时施加动载，在动载作用下各监测点的位移时程曲线如图9所示。

图8 不同深度监测点分布示意

图9 隧道开挖至不同位置时施加动载地层不同深度监测点位移时程曲线

隧道开挖至不同位置施加动载地层不同深度监测点最大位移值如表4所示。

通过对隧道开挖至不同部位施加动载地层不同深度监测点位移时程曲线及最大位移值分析可知:

(1)随着地层深度的增加，在动载作用下产生的位移不断减小，地表处监测点位移最大，隧道拱顶处位移最小。这说明振动荷载在地层中传播时，由于地层阻尼等因素使振动波能量不断减小。

(2)地层动力响应从地表到隧道拱顶衰减速度逐渐减小。

(3)隧道开挖至25 m处施加动载，地层不同深度各监测点的位移值较大。

5.4 地层应力响应分析

为分析在列车通过时地层的竖向应力变化情况，通过对地层监测点(图8)进行监测分析，得到不同深度处地层在列车振动荷载作用下的竖向应力时程曲线，如图10所示。

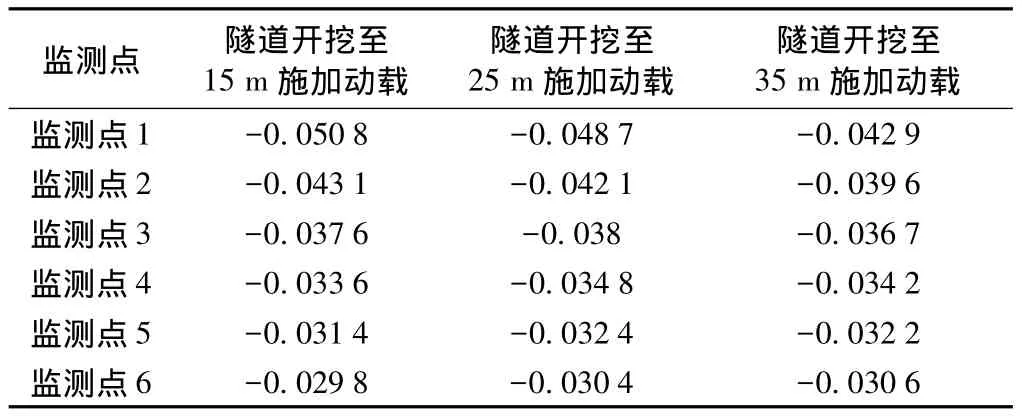
表4 地层不同深度监测点最大位移值 mm

隧道开挖至不同位置施加动载地层不同深度监测点最大应力值如表5所示。

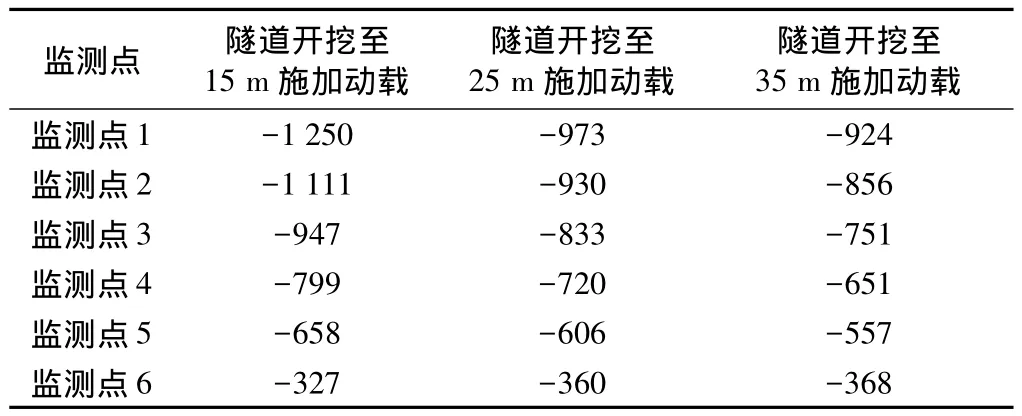
表5 隧道开挖至不同位置施加动载地层不同深度监测点应力最大值 Pa

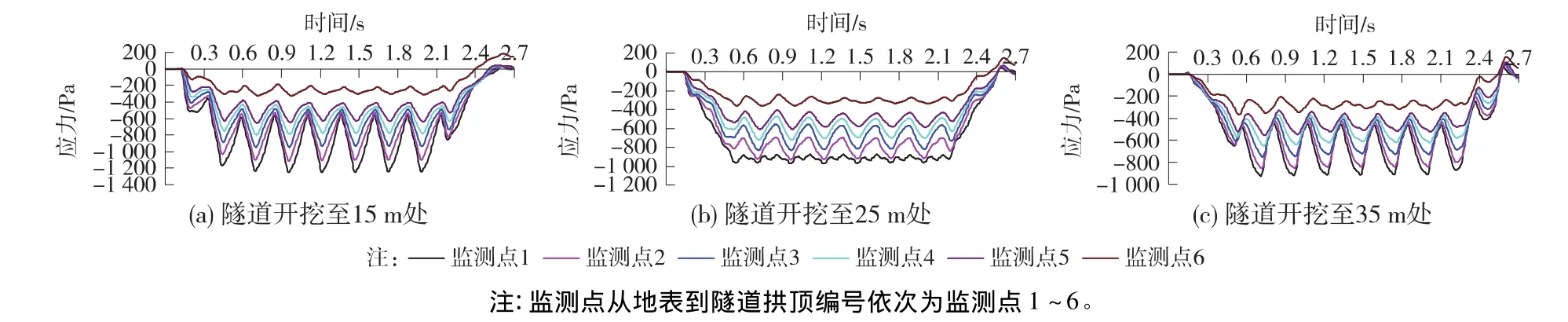
图10 隧道开挖至不同位置时施加动载地层不同深度监测点应力时程曲线

通过对隧道开挖至不同部位施加动载地层不同深度监测点应力时程曲线及应力最大值分析可知:

(1)随着地层深度的增加，在动载作用下产生的竖向应力不断减小，地表处监测点沉降最大，隧道拱顶处沉降最小。这说明振动荷载在地层中传播时，由于地层阻尼等因素使振动波能量不断减小。

(2)地层动力响应从地表到隧道拱顶衰减速度逐渐减小，但是隧道拱顶附近衰减较快，这主要可能是由于隧道拱顶的压力拱效应造成的。

(3)随着隧道开挖的不断推进，开挖面即掌子面处不同深度地层在列车动载作用下的竖向应力在不断减小，这主要是因为隧道开挖深度越深，高速铁路路基与下穿隧道交叉处的“临空面”面积不断增加，地层在列车动载作用下向隧道净空发生位移，使应力在一定程度上释放。

6 结语

通过对隧道施工至不同位置时列车以时速350 km通过，研究地表及地层不同位置处位移值的变化，结论如下。

(1)在单次列车动载作用下产生的位移值与隧道开挖引起的沉降量相比很小，可以忽略不计。但是根据国内外工程实际，在长期高速列车振动荷载的作用下地层产生的沉降量不能忽视。

(2)下穿隧道与高速铁路路基交叉点处为该工程薄弱环节，因此，在设计与施工时要注意对该处进行加强。

(3)隧道开挖后，特别是上台阶开挖后，应立即施加支护。

(4)埋深对地层沉降影响比较明显，随着地层深度的增加，在动载作用下产生的沉降不断减小，并且地层动力响应从地表到隧道拱顶衰减速度逐渐减小。与日本E rich iTan igueh i的研究结果一致［12］。

［1］贺斯进，蔺云宏.地铁盾构区间穿越铁路站场设计与施工分析［J］.现代隧道技术，2012，49(3):166.

［2］索然绪.雅泸高速公路徐店子隧道洞口段地震动力响应研究［D］.成都:西南交通大学，2007.

［3］陈卫忠，等.ABAQUS在隧道及地下工程中的应用［M］.北京:中国水利水电出版社，2010.

［4］傅鑫彬.浅埋软弱围岩大跨隧道的施工技术研究［D］.成都:西南交通大学，2006.

［5］徐林生，等.洋碰隧道CRD工法施工过程的动态仿真数值模拟研究［J］.地质灾害与环境保护，2001，12(1):58-62.

［6］朱正国，等.铁路隧道下穿公路引起的路面沉降规律和控制基准研究［J］.岩土力学，2012，33(2):559-563.

［7］房明，等.新建隧道盾构下穿施工对既有隧道影响的三维数值模拟［J］.铁道科学与工程学报，2011，8(1):68-71.

［8］陈灯红，等.基于ABAQUS的黏弹性边界单元及在重力坝抗震分析中的应用［J］.世界地震工程，2010，26(3):128-129.

［9］刘晶波，等.三维黏弹性静-动力统一人工边界［J］.中国科学，2005，35(9):967-979.

［10］孙海峰，等.ABAQUS中动力问题边界条件的选取［J］.地震工程与工程振动，2011，31(3):72-76.

［11］翟婉明.列车-轨道-桥梁动力相互作用理论与工程应用［M］.北京:科学出版社，2011.

［12］李晓霖.地铁诱发振动对地面以及地上结构的影响规律研究［D］.北京:北京工业大学，2003.