土质路基板式无砟轨道基床动力特性研究

孔祥辉，张思峰，蒋关鲁，董志泓

(1.山东建筑大学交通工程学院，济南 250101;2.西南交通大学土木工程学院，成都 610031)

高速、重载是当今世界铁路发展的趋势，机车轴重的增大和速度的提高，使列车与线路系统的动力相互作用大幅加剧［1-5］。为了提高轨道在列车高速运行时的稳定性和平顺性，减少轨道的维修和养护，自20世纪60代初，世界各国铁路相继开展了以用混凝土、沥青混合料等整体固化道床替代散粒体道砟，即无砟轨道结构的系统研究，如今一些国家和地区已经把采用无砟轨道作为发展高速铁路的主要技术政策［6］。现阶段土质路基上无砟轨道结构的设计与内力分析通常采用弹性地基上梁板理论来解决［7-9］，温克勒(Winkler)地基模型因其假设条件简单，在设计中得到了广泛应用。在使用温克勒模型对土质路基无砟轨道进行分析时，路基中动应力的分布规律和基床反力系数的取值是建立合理的路基支承刚度的重要前提条件。一般来讲，路基的支承刚度和基床反力系数即使在弹性领域内也呈现很明显的非线性关系［10］，产生这种非线性关系的主要原因有以下3点:①荷载大小;②变形大小;③荷载作用时间的长短。

要解决基床反力系数取值难的问题，首先要掌握路基在列车循环荷载作用下的动态响应，尤其是基床范围内的动力特性［11，12］。结合遂渝线无砟轨道综合试验段，通过室内大比例基床动力模型试验，研究了动应力和动位移在路基横断面及沿深度方向的分布特征，在此基础上，探讨了路基动应力和基床反力系数的求解方法。

图1 无砟轨道基床动力模型(单位:m)

1 基床动力模型试验

1.1 试验简介

无砟轨道结构从上到下依次为钢轨、轨道板、CA砂浆层和混凝土基础板，为了简化设计，在满足测试要求的前提下，将轨道板和CA砂浆层一并折算到混凝土基础板里。路基基床原型为遂渝线无砟轨道综合试验段单线路堤，基床表层为A组填料，压实系数K≥0.98，孔隙率 n＜18%;基床底层为 A、B 组填料(灰岩风化层，属碎石类土)，压实系数 K≥0.95，孔隙率 n＜28%;路基边坡坡度为1∶1.5。

无砟轨道基床模型［10，13］的结构尺寸、仪器埋设及加载装置见图1，混凝土基础板纵向长度为1.12 m，厚度为0.2 m。按平面应变问题考虑，线路纵向采用固定钢板挡墙模拟其边界条件。循环加载共分9级(41.5-51.5，36.5-56.5，31.5-61.5，26.5-66.5，21.5-71.5，16.5-76.5，11.5-81.5，6.5-86.5，0-93 kN)，波形为正弦波，频率为 6 Hz，每级循环加载6 000次。

1.2 试验结果

图2为路基表面的动应力和动位移在1～9级循环荷载下的横向分布形式。可以看出，随着外加荷载的增大，基床的动态响应越来越强烈，即动应力和动位移是不断增大的。动应力在路基横断面上呈不均匀分布，轨下的动应力值最大，中线下次之，基础板边缘最小，即所谓的马鞍形分布，并且随着动荷载的增大，这种不均匀性越来越明显。动位移计只设在轨下和中线位置处，其在路基横断面上的分布规律与动应力基本类似。

图3为分级循环荷载作用下，轨下动应力和动位移沿基床深度的分布形式。可以看出，二者随深度的增加都是逐渐减少的，在基床表层内衰减较快，在基床底层内衰减的较慢。

图2 路基表面动态参数的横向分布

图3 轨下动态参数沿基床深度分布

2 动应力计算方法

对于有砟轨道结构，张千里［14］介绍了用Odemark理论和弹性理论计算路基动应力的方法。对于无砟轨道而言，如果知道基础板底的荷载分布，用上述计算动应力同样有效。

由上面的讨论可知随着荷载的增大，路基面动应力的横向分布越不均匀，但根据圣维南原理，荷载分布形式的差异只对附近的应力有影响。为了计算方便，假设无砟轨道基础板底面动应力为横向均匀分布，纵向为三角形分布［15］。

Odemark模量与厚度当量换算公式

Boussinesq应力解

对带电粒子进行如下分析，带电粒子受到一个竖直向下的恒力电场力的作用，并且射入平行板电容器时带有一个水平的初速度v0。带电粒子在水平方向上做的是匀速直线运动，在竖直方向上做的是初速度为零的匀变速直线运动。这种运动类似于物体在重力作用下只受到一个水平初速度的平抛运动。所以可根据平抛运动的相关知识来解有关题目，可以求得以下有关物理量或相关结论：

式中 Ei——各路基层压缩模量;

E0——底层压缩模量;

he——换算厚度;

P0——轨枕底动应力，m=L/B，n=z/B;

L——荷载的长边;

B——荷载的短边;

z——荷载角点下的深度。

图4为无砟轨道模型试验在1级、5级和9级荷载下路基动应力的计算值和实测值，二者很接近，说明把路基面动应力近似看作横向均匀分布是可行的。

3 基床反力系数

对土质路基无砟轨道进行结构设计时通常采用温克勒(Winkler)地基模型，它假定基础板底面任一点所受的压力与该点的位移成正比，即p=ks，其中k为基床反力系数，其取值正确与否直接影响到设计结果的合理性。设计中k值通常采用以下方法来确定:(1)大型载荷板试验;(2)k值和K30的关系;(3)经验值。由载荷板试验得到的k值较准确，但试验费工费力，而K30法和经验取值均存在较大的误差。

图4 动应力(轨下)计算值与实测值

3.1 推导过程

铁路路基为多层结构形式，各层间的弹性模量和泊松比均不相同，而Winkler地基模型假设路基是均质单层土，所以要计算基床反力系数，首要任务是将多土层体系转换为均质单土层。

将各土层假设为一维压缩模型，即土层只在竖向发生变形。根据式(3)计算各土层的压缩模量Esi。

式中 Es——压缩模量;

E——弹性模量;

ν——泊松比。

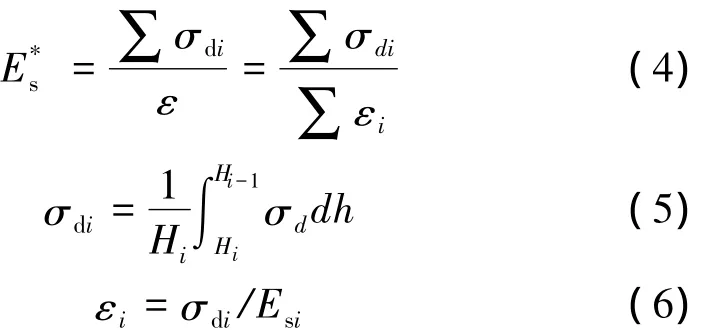
式中，σdi，εi，Hi和 Esi分别为第 i层土的平均动应力、动应变、厚度及压缩模量。

动应力和动变形随路基深度的增加都是减小的，从理论上讲，深度无限增加，变形虽在减少，但不致为零。从实用角度看，在适当深度以下，变形可近似的当作零，这个深度视为土层的有限压缩层厚度H0，由式(7)确定

式中，γ为土的容重。应当注意的是，当计算的压缩层厚度H0大于实际各土层总厚度H时，取H0=H，这样，就可以根据式(4)和式(7)将多土层体系转化为均质单土层，如图5所示。

图5 多土层体系转化为均质单土层

再将均质单土层分成多个厚度很小的薄层，每一层的应力、应变和厚度分别为 σdj，εj和hj，则变形

上式的计算示意如图6所示，其中Ae为区域OBCD的面积。

图6 均质单土层动应力沿深度分布

Winkler地基模型是假设土层各处的受力都是相同的，各处的应变也相同，其变形

式中，He为Winkler地基等效深度(图6)，σd0为土层表面动应力，将式(8)代入式(9)可得

基床反力系数可由下式得到

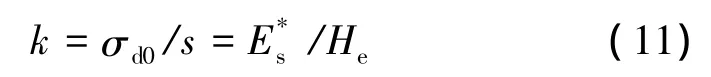
根据式(10)和式(11)可将均质单层土转化为等效Winkler地基模型，如图7所示。

3.2 试验验证

表1为不同工况下二层路基结构的基床反力系数k的计算值与实测值，其中级配碎石参数为:E=180 MPa，ν=0.3;A、B 组填料:E=110 MPa，ν=0.3。

图7 均质单层土转化为等效Winkler地基

由表1可知，1～9级荷载下k的计算值和实测值的偏差为1%～9%。计算值和实测值比较接近，说明上述将多土层体系转化为等效Winkler地基模型的方法是切实可行的。

表1 二层路基结构k的理论计算值和实则值kPa/mm

4 结语

(1)随着外加动荷载的增大，路基基床的动力响应越来越强烈。动应力和动位移在路基横断面上都呈不均匀分布，且随着动荷载的增大，这种不均匀性越来越明显。沿路基深度方向，动应力和动位移随深度的增加逐渐减小，并且在基床表层衰减较快，在基床底层衰减较慢，可见基床表层承担了大部分的动荷载。

(2)将无砟轨道基础板底面的动应力简化为沿横向均匀分布，沿纵向三角形分布，联合Odemark理论和弹性理论计算基床动应力，所得计算值和实测值很接近。

(3)在动应力分布已知的前提下，将路基各土层假设为一维压缩模型，并确定合理的压缩层厚度，在此基础上，提出了一种将多土层体系转换为等效Winkler地基模型的方法;采用此法所得基床反力系数的理论值与实测值的偏差在10%以内，证实了计算方法是有效的。

［1］魏永幸，蒋关鲁.客运专线无砟轨道路基关键技术探讨-以遂渝线无砟轨道综合试验段为例［J］.铁道工程学报，2006(5):39-44.

［2］周萌，宫全美，王炳龙，等.路基不均匀沉降值对板式轨道动力响应的影响［J］.铁道标准设计，2010(10):1-4.

［3］陈建国，肖军华.提速列车荷载作用下铁路路基动力特性的研究［J］.岩土力学，2009，30(7):1944-1950.

［4］宋小林，翟婉明.高速移动荷载作用下CRTSⅡ型板式无砟轨道基础结构动应力分布规律［J］.中国铁道科学，2012，33(4):1-7.

［5］张鹏飞，雷晓燕，高亮，等.货物列车运行引起的大地振动及其对精密仪器的影响［J］.铁道科学与工程学报，2013，10(2):108-111.

［6］詹永祥，蒋关鲁.无砟轨道路基基床动力特性的研究［J］.岩土力学，2010，31(2):392-396.

［7］Auersch，L.Dynamic interaction of various beams with the underlying soil-finite and infinite，half-space and Winkler models［J］.European Journal of Mechanics(A/Solids)，2008(27):933-958.

［8］Tatsuya Ishikawa，Etsuo Sekine，Seiichi Miura.Cyclic deformation of granular material subjected to moving-wheel loads［J］.Canadian Geotechnical Journal，2011(48):691-703.

［9］李春霞，殷明旻，车晓娟.路基上无砟轨道基床反力系数取值的探讨［J］.铁道建筑，2009(11):76-79.

［10］蒋关鲁，孔祥辉，孟利吉，等.无砟轨道路基基床的动态特性［J］.西南交通大学学报，2010，45(6):855-862.

［11］边学成，陈云敏.列车移动荷载作用下分层地基响应特性［J］.岩石力学与工程学报，2007，26(1):182-189.

［12］陈仁朋，王作洲，蒋红光，等.Ⅰ型轨道-路基系统动力荷载放大系数模型试验研究［J］.岩土力学，2013，34(4):1045-1052.

［13］冯立臣，蒋关鲁，王智猛，等.客运专线土质路基无砟轨道基床动态特性的模型试验研究［J］.铁道建筑，2008(8):78-81.

［14］张千里，韩自力，吕宾林.高速铁路路基基床结构分析及设计方法［J］.中国铁道科学，2005，26(6):53-57.

［15］董亮，赵成刚，蔡德钩，等.高速铁路无砟轨道路基动力特性数值模拟和试验研究［J］.土木工程学报，2008，41(10):81-86.