三点弯钎焊接头裂纹扩展数值模拟*

陈 兴 周帼彦 舒双文 王琼琦 朱奎龙

(华东理工大学机械与动力工程学院承压系统与安全教育部重点实验室)

为了提高循环效率，高温气冷堆通常使用单位体积换热面积大、传热效果好的板翅式回热器来预热氦气。板翅式回热器中板翅结构的钎焊焊缝具有夹杂及气孔等诸多缺陷，是回热器中最脆弱、最容易形成裂纹的区域。张青科等对奥氏体不锈钢钎焊焊接面裂纹形成机制进行了试验研究，结果表明真空钎焊可以较好地抑制裂纹的形成[1]。沈春来对单个钎焊翅形结构进行了强度分析，结果表明钎缝厚度和钎焊温度是影响钎焊结构强度的主要因素[2]。但目前对钎焊接头的研究主要集中在钎焊工艺优化方面[3～7]，而对钎焊接头裂纹扩展规律的研究还鲜有报道。

由于钎焊焊缝通常很薄(小于100μm)，因此试验法很难研究钎焊接头的裂纹扩展特性。近年来，随着计算机技术的不断发展，有限单元法的日益成熟为断裂力学研究提供了新途径。19世纪60年代，Rice J R提出使用J积分来表征裂纹尖端的应力场强度[8]，但J积分法只能用来模拟裂纹尖端的应力场，并不适用于模拟裂纹的扩展过程。扩展有限元法(XFEM)形成于20世纪90年代，可用于模拟裂纹沿任意路径的扩展，但目前XFEM技术还不够成熟，需要在模型中预制初始裂纹，因此不能模拟裂纹的起裂。1994年Needleman A在前人研究的基础上提出了基于牵引力分离法则的内聚力模型，该模型假设裂尖的牵引力是分离位移的函数，从而避免了线弹性力学中裂纹尖端的应力奇异性，且使用时不需要预制裂纹源，可以很好地模拟界面裂纹的起始和扩展过程，目前已经广泛应用于土木、胶黏剂、地质及复合材料等领域[9～12]。

笔者将内聚力模型引入钎焊接头裂纹扩展研究中，使用ABAQUS有限元分析软件模拟三点弯钎焊试样的裂纹扩展过程，进而分析钎焊接头裂纹的扩展规律，为此类接头的安全服役提供理论依据。

1 内聚力模型

内聚力模型基于损伤力学观点，认为在裂纹尖端存在一个微小的内聚力区。内聚力区的尺寸是一个很小的常数，并且与加载方式无关[13]。可以认为，内聚力区是从材料开始损伤到形成微裂纹的区域(图1)。在这个区域内，材料在张力作用下被逐渐拉伸的过程中会出现微孔洞及微裂纹等缺陷，造成结构承载力下降。这些独立的缺陷逐渐增大并相互连结形成大的缺陷，最终扩散到整个承载面，致使材料产生裂纹形成新的裂纹尖端，使裂纹向前扩展。

图1 内聚力区简化示意图

在内聚力区内，通常视牵引力T为裂纹上下表面分离位移δ的函数，即牵引力-位移法则[14]：T=f(δ)。双线性牵引力-位移法则是一种简单且有效的内聚力模型法则。在内聚力区内，应力值随着分离位移的增大而增大：当应力达到临界值σmax时，内聚力区开始出现损伤，应力值随之下降；当应力值降为0时，该处材料不再具有承载能力，即发生裂纹扩展。

对于多向混合开裂，双线性内聚力模型的控制方程如下：

式中Tn,s,t——各向应力；

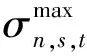
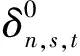
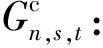
2 有限元模拟

2.1有限元模型

笔者在ABAQUS有限元分析软件中建立钎焊接头三点弯试样的有限元模型。为了减小有限元模型的规模，支撑滚柱和上压头采用解析刚体。316L不锈钢的弹性模量E为199GPa，泊松比μ为0.3；BNi-2钎料的临界内聚能Gc为16.17kJ/m2，损失起始应力σmax为25 MPa[15]。

不锈钢母材使用平面应变单元CPE4R进行划分。考虑到钎缝厚度与母材尺寸相比非常薄，笔者将裂纹沿着钎缝的扩展视为界面开裂，并利用内聚力单元来模拟钎焊焊缝的开裂行为。相关研究认为使用2～5个内聚力单元对应一个母材单元比较合理[16,17]，笔者采用一对四的方式进行网格布置，即1个母材单元对应4个内聚力单元。最终划分的内聚力单元尺寸为25μm，与之相邻的母材单元最小单元尺寸为0.1mm，单元总数为16 163个，网格划分结果如图2a所示。内聚力单元与平面应变单元之间采用tie绑定约束(图2b)；试样与滚柱、试样与上压头之间设置摩擦系数为0.2的表面对表面接触属性；对两滚柱中心设置固定约束。此外，为了防止有限元分析过程出现刚体位移，建模时需限制上压头与试样接触点的横向位移。

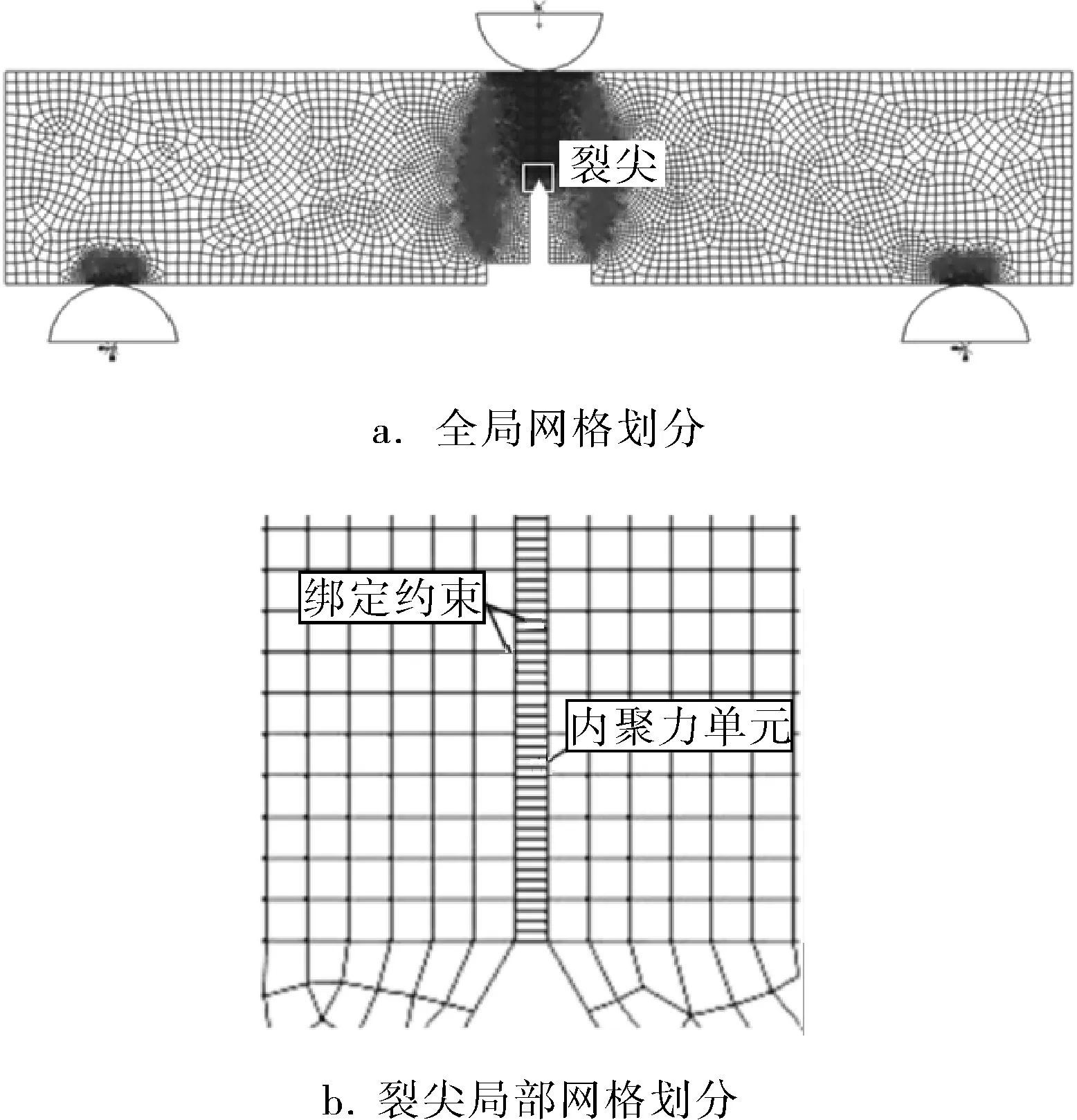
图2 网格划分结果

2.2模拟结果

将建立好的有限元模型提交运算，在计算过程中，可以随时通过ABAQUS生成的子文件查看计算进程。在起裂之前，计算过程比较稳定，每个时间增量步只需一次迭代运算；开裂后，每个增量步需要迭代两次或多次，因此计算速度比起裂之前慢。运算结束后，提取模型中施加的载荷与裂尖单元相对位移的变化关系(图3)。由图3可知：在起裂之前，载荷随着试样缺口张开位移COD的增大而快速上升；在起裂瞬间，试样能承受的载荷达到临界值1 392.29N；起裂后，随着裂纹的不断扩展，接头的承载面积越来越小，维持裂纹扩展所需要的载荷也逐渐减小。

图3 载荷-裂尖张开位移曲线模拟值

3 三点弯试验

3.1试样制备

笔者使用的钎焊母材是直径为φ50mm的316L不锈钢棒。钎料为宽20mm、厚40μm的非晶态箔状镍基钎料BNi-2。箔状BNi-2钎料通常采用急速冷却方法制造，厚度均匀，最薄可加工至35μm，并能保持良好的塑性和韧性，易于加工成型。BNi-2钎料中一般会掺入3%左右的B元素以降低钎料的熔点，其中固相线温度为971℃，液相线温度为999℃，BNi-2镍基钎料的主要化学成分见表1。

表1 BNi-2镍基钎料主要化学成分 %

为了提高钎焊质量，需要对切割后的不锈钢棒材焊接面进行打磨和抛光处理。抛光后的不锈钢和钎料表面沾有油污、灰尘和其他残留物质，需要对其进行清洗。首先将316L母材和箔状BNi-2钎料用清水洗净，然后用酒精仔细擦拭不锈钢和钎料表面，对于顽固油污可进一步用丙酮进行清洗，最后将处理好的材料密封保存备用。

316L/BNi-2钎焊接头三点弯曲试样是从焊后的不锈钢棒中取样的，试样尺寸根据金属材料断裂韧性测试方法设计，厚10mm，宽20mm，长100mm，具体尺寸和加工精度要求如图4a所示。在试样一侧焊缝位置切割长度为10mm的缺口，缺口底角为60°。为了便于装夹引伸计，在缺口外开深2mm、宽10mm的刀口(图4b)。

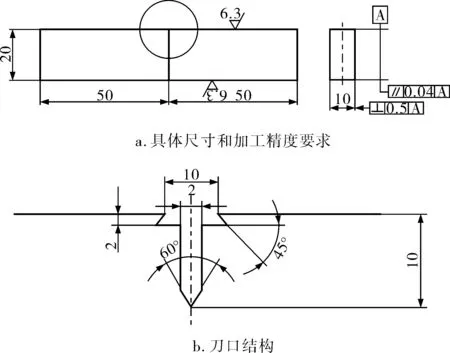
图4 316L/BNi-2钎焊接头三点弯曲试样

3.2试验方案

三点弯曲试验在Instron万能试验机上进行。首先将试样对称放置在两个间距为80mm的支撑滚柱之间，调整试样位置，保证试样的厚度方向与两支撑滚柱的轴向方向平行；然后向下调整试验机上压头使之轻触试样，观察压头位置是否与焊缝重合，若不重合，则需继续调整；最后启动试验机进行加载(图5)。本次试验所有试样的加载速率均为0.01mm/s。

图5 试样的固定和加载

3.3试验结果

试验得到的两个试样的载荷-裂尖张开位移曲线如图6所示，从图6可以看出：初始阶段施加在上压头上的载荷随着裂尖张开位移的增大而增大；当钎缝位置发生起裂时，载荷值达到最大，两次试验得到的最大载荷为1 267.05、1 491.97N；起裂之后，随着裂尖张开位移的继续增大，驱动裂纹向前扩展所需的载荷开始逐渐减小。

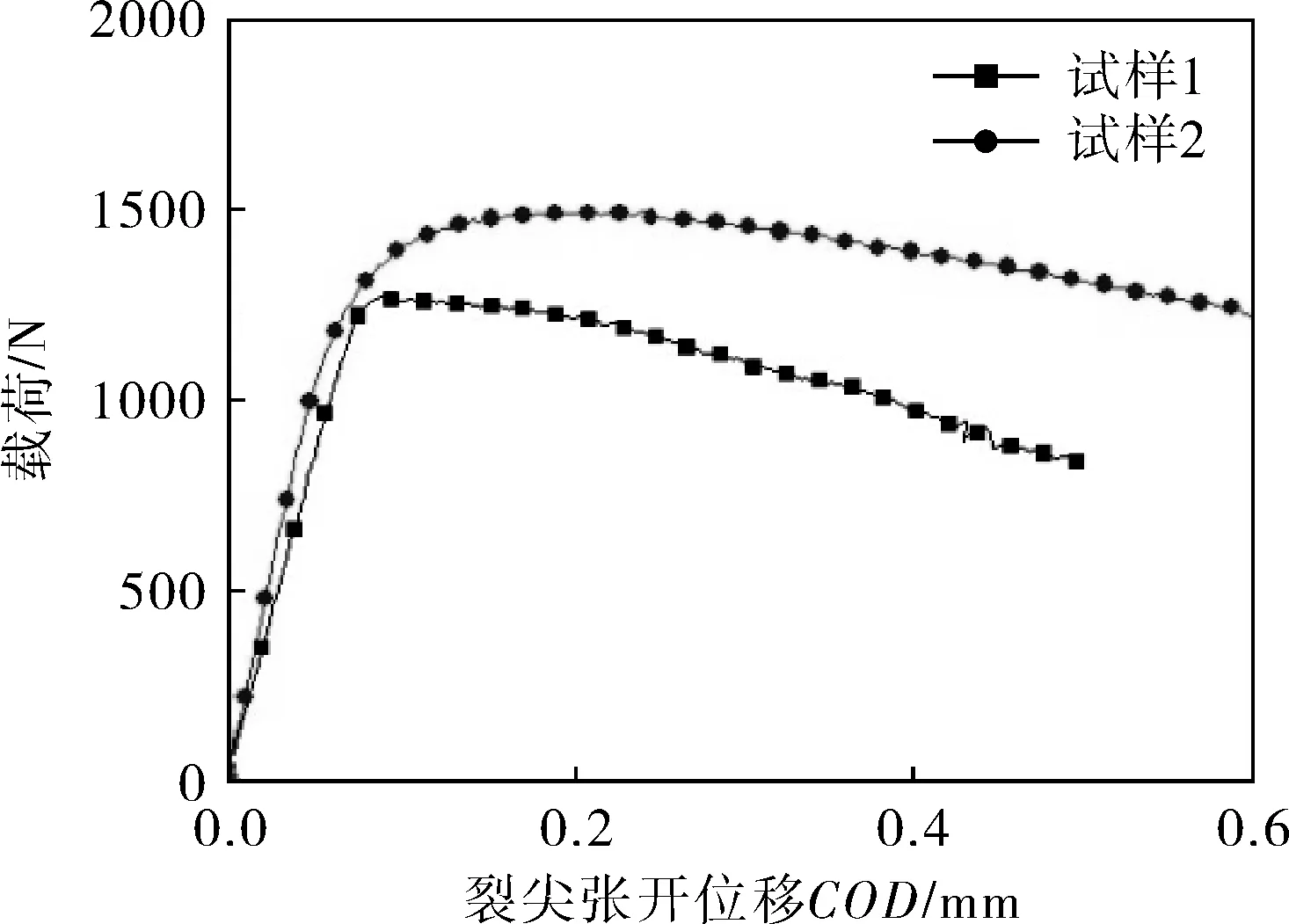
图6 试样的载荷-裂尖张开位移曲线

4 分析与讨论

4.1结果比较

图7为试样载荷-裂尖张开位移曲线的模拟值和试验值。从图7可以看出：模拟得到的载荷-裂尖张开位移曲线与两次试验平均值吻合较好，模拟得到的最大载荷为1 392.29N，与试验均值1 364.83N很接近。从图7中还可以看到裂纹从萌生到扩展的全过程：在起裂之前，施加在上压头的载荷随着钎缝张开位移的增大而不断增大；起裂后，随着裂纹的不断扩展，接头的承载面积不断减小，驱动裂纹向前扩展所需要的载荷也随之降低。

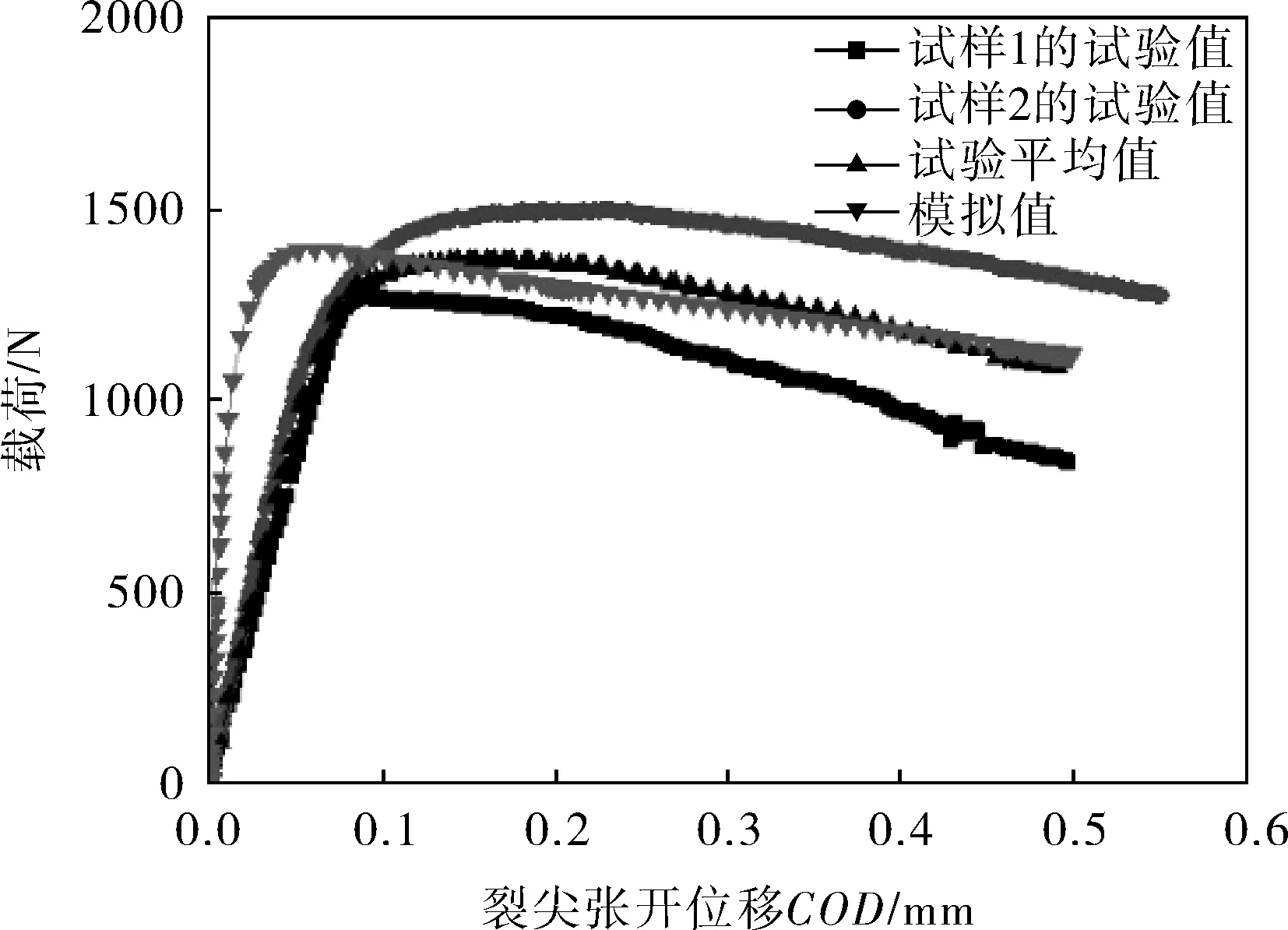
图7 试样载荷-裂尖张开位移曲线的模拟值与试验值

4.2裂纹扩展规律分析

图8解释了内聚力模型模拟裂纹起裂和扩展规律。图8中坐标0表示T型钎焊接头有限元模型中焊缝边缘所在位置，横坐标表示钎焊焊缝到焊缝边缘的距离，纵坐标表示钎缝各位置的单元牵引力。开始加载后，随着位移载荷的不断增大，钎缝上的单元牵引力逐渐变大，此阶段的牵引力T在钎缝边缘达到最大值(曲线1);当牵引力T达到损伤起始应力σmax时，内聚力单元开始出现损伤，损伤的不断累积造成内聚力单元承载能力开始下降(曲线2)；内聚力单元损伤值达到临界值之后完全失去承载能力；曲线3表示钎缝边缘的内聚力单元牵引力降到0时发生起裂；曲线4表示起裂后的裂纹已经扩展到了钎缝内部更深的位置。

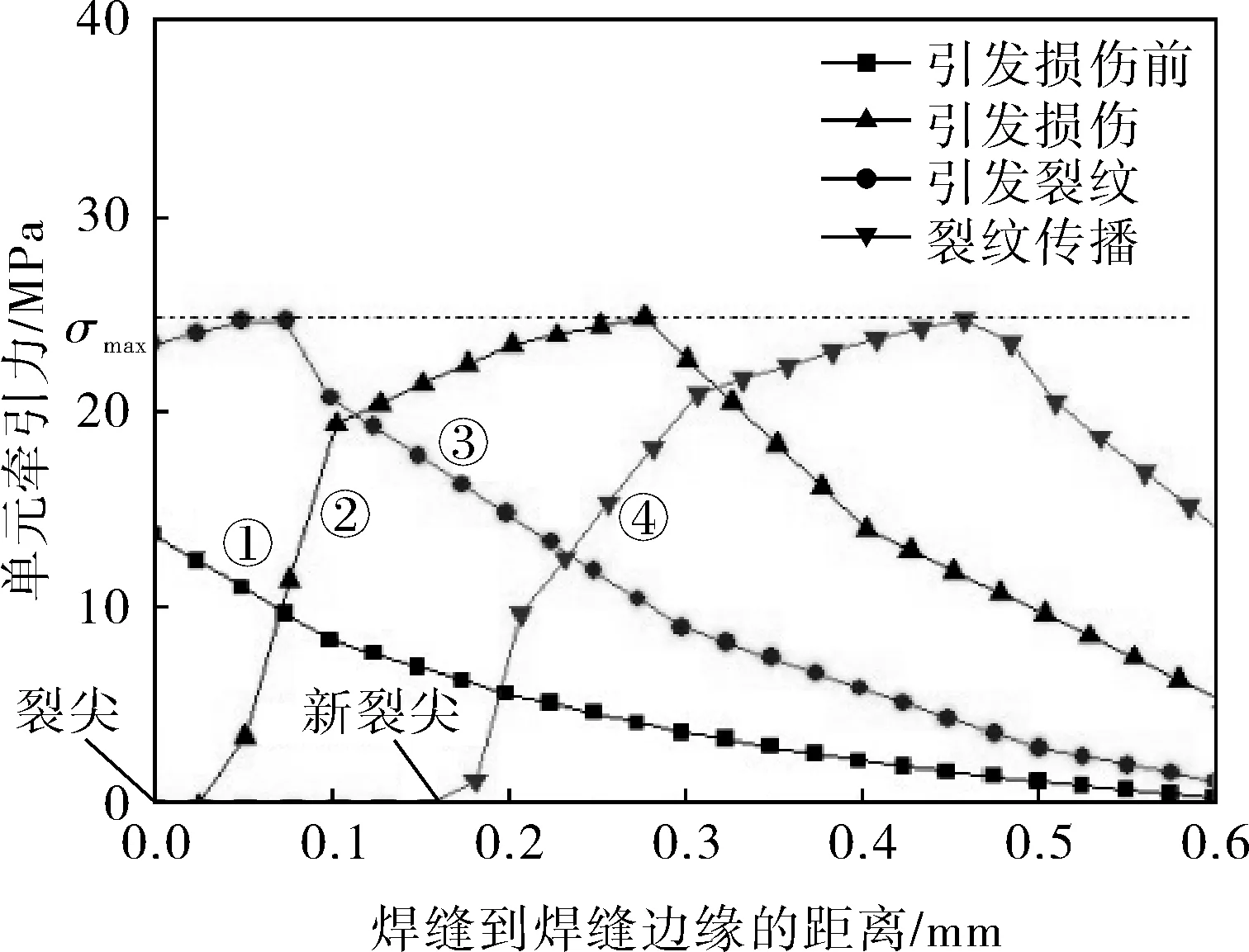
图8 钎缝位置上内聚力单元牵引力变化

5 结论

5.1模拟得到的钎焊接头三点弯曲试样起裂时的最大载荷为1 392.29N，与试验结果1 364.83N很接近。且在裂纹扩展阶段，数值模拟结果和试验结果吻合较好，说明内聚力模型可以很好地预测三点弯钎焊接头的裂纹扩展。

5.2内聚力模型从损伤累积的角度解释了钎焊接头裂纹起裂和扩展规律：当内聚力单元应力达到临界值时σmax，内聚力单元开始出现损伤累积，出现损伤的内聚力单元承载能力逐渐下降；当单元应力降为0时，内聚力单元因完全失去承载能力而被删除，从而形成新的裂纹前沿，推动裂纹不断向前扩展。

[1] 张青科，裴夤崟，龙伟民.奥氏体不锈钢钎焊界面裂纹形成机制研究[J]. 金属学报， 2013，49(10): 1177～1184.

[2] 沈春来.高压板翅式换热器的强度与失效分析[J]. 深冷技术，1997，5(3): 7～10.

[3] 蒋文春，巩建明，涂善东. 冷却方式对304不锈钢板翅结构强度和微观组织的影响[J]. 压力容器，2009，26(11): 16～20.

[4] Nishi H, Kikuchi K. Influence of Brazing Conditions on the Strength of Brazed Joints of Alumina Dispersion- strengthened Copper to 316 Stainless Steel[J]. Journal of Nuclear Materials, 1998, 258～263: 281～288.

[5] Chen S, Chin B A. Low Activation Braze Joint of Dispersion-strengthened Copper[J]. Journal of Nuclear Materials, 1995, 225: 132～136.

[6] 于治水，李瑞峰，祁凯，等. BNi-2+BNi-5复合钎料钎焊316L不锈钢接头界面组织及分析[J]. 江苏科技大学学报(自然科学版)，2008，22(5): 28～32.

[7] Philips N R, Levi C G, Evans A G. Mechanisms of Microcrack Evolution in an Austenitic Stainless Steel Bond Generated Using a Quaternary Braze Alloy[J]. Metallurgical and Materials Transactions, 2008， 39(1): 142～149.

[8] 解德，钱勤，李长安. 断裂力学中的数值计算方法及工程应用[M]. 北京：科学出版社，2009.

[9] Chen G M, Chen J F, Teng J G. The Behavior of FRP-to-concrete Interfaces Between Two Adjacent Cracks: A Numerical Investigation on the Effect of Bondline Damage[J]. Construction and Building Materials, 2012, 28(1): 584～591.

[10] 杨小辉，胡坤镜，赵宁，等. 内聚力界面单元在胶接接头分层仿真中的应用[J].计算机仿真，2010，27(10)：317～320.

[11] Yang Q D, Thouless M D, Ward S M. Analysis of the Symmetrical 90-peel Test with Extensive Plastic Deformation[J]. The Journal of Adhesion, 2000, 72(2): 115～ 132.

[12] Reedy Jr E D, Mello F J, Guess T R. Modelling the Initiation and Growth of Delaminations in Composite Structures[J]. Journal of Composite Material, 1997, 31(8): 812～831.

[13] 张军. 界面应力及内聚力模型在界面力学的应用[M]. 郑州：郑州大学出版社，2011.

[14] Elices M, Guinea G V, Gómez J, et al. The Cohesive Zone Model: Advantages, Limitations and Challenges[J]. Engineering Fracture Mechanics, 2002, 69(2):137～163.

[15] 陈兴，舒双文，周帼彦，等. 基于内聚力模型的T型钎焊接头裂纹扩展数值模拟[J]. 压力容器，2014，31(8)：7～13,58.

[16] Zhou F H, Molinari J F, Shioya T. A Rate-dependent Cohesive Model for Simulating Dynamic Crack Propagation in Brittle Materials[J]. Engineering Fracture mechanics, 2005,72(9): 1383～1410.

[17] Turon A, Dávila C G, Camanho P P, et al. An Engineering Solution for Mesh Size Effects in the Simulation of Delamination Using Cohesive Zone Models[J]. Engineering Fracture Mechanics, 2007, 74(10): 1665～1682.