换热器污垢特性的建模与预测*

文孝强 苗庆龙 孙灵芳

(东北电力大学)

国内外学者按照污垢形成的主要物理/化学过程划分，在污垢预测技术方面取得了许多成果：McGuire J和Swartzel K R提供了沉积率与表面能(或表面张力)的经验关系式[1]。Müller-Steinhagen H等提出了表面沉积新判据[2]。Xu Z M和Yang S R重新定义了污垢的诱导期[3，4]。Yang C F等提出了碳酸钙析晶垢沉积率预测模型[5]，并对其诱导期内和以后的沉积机理进行了探讨[6]。Zubair S M等则从换热器维护的统计策略出发提出了碳酸钙的统计分析模型[7，8]，用于评估污垢费用[9]。Epstein N根据文献[10～14]的研究，归纳出颗粒污垢 “自阻滞”现象的3个通用机理[15]。Yang S R等采用分形理论并运用导热与逾渗的类比，建立了均匀散体导热热阻的逾渗模型[16～18]；张海林等进而应用于具有一定颗粒分布的灰层污垢热阻的确定，可望为颗粒污垢热阻的预测提供可测参数表述的计算模型[19，20]。Crittenden B D等评述了该领域10余年的进展，并得出对化学反应污垢的形成机理和重要的工艺过程参数影响的认识还远未完成，仍需要进一步研究这一结论[21]。此外，Fernandez-Torres M J等基于传热传质理论，得到了凝固污垢分析模型[22]。徐志明等基于污垢形成的随机性，利用概率方法推导出了考虑初始污垢热阻影响的污垢模型[23]。

经过人们不懈努力，对污垢形成的基本物理、化学过程方面有了进一步的认识，积累了许多宝贵污垢的资料和实验数据[24～30]。近些年，基于知识的智能理论和方法在污垢的预测研究中得到了关注：付亚荣等利用BP网络对油田地面集输管道结垢进行预测和评判[31]。Enrique T等针对电厂煤粉锅炉的结垢，采用BP网络进行了在线监测和预测[32]。侯迪波等针对间歇换热设备的周期性结垢现象提出了一种基于模糊神经网络的周期性结垢预测方法[33]。樊绍胜和王耀南采用T-S模糊模型描述软垢和硬垢的增长趋势[34]。彭珍等利用三层前馈网络对换热管污垢热阻进行预测，预测值与实测值基本吻合，误差较小[35]。虽然不断有研究者提出新的污垢预测模型，然而至今还没有一个被普遍接受的模型。其原因在于污垢的形成过程过于复杂，对污垢形成的微观机理还没有完全认识清楚。

偏最小二乘算法可以实现因变量对自变量的回归，涵盖自变量系统信息的同时，能较好地解释因变量，解决了自变量间多重相关性情况下的建模问题，适合小样本容量的回归建模，可以有效排除系统噪声干扰。另一方面，相对来说，环境温度等参数的获得比较容易，而且节省人力和物力，由温度等参数推测污垢热阻值可实现换热设备污垢热阻的在线监测。因此，笔者将壁温、流速、出、入口温度等参数作为输入，以光管换热器为主要研究对象，利用偏最小二乘分析处理方法对换热器污垢特性进行了实验、建模和预测研究。

1 偏最小二乘算法

偏最小二乘算法为求解下列优化问题[36，37]：

max(E0w1,F0c1)

(1)

变换为拉格朗日算法形式为：

(2)

分别对Γ求λ1，λ2，w1，c1的偏导数，并令其为0，则：

(3)

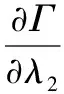
(4)

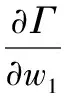
(5)

(6)

由上式可推导出：

(7)

则ζ1便是优化问题的目标函数值。经过求解可得：

(8)

(9)

于是，可得E0和F0对t1的回归方程：

(10)

(11)

用残差矩阵E1、F1取代E0、F0，求第二个轴w2、c2以及第二个成分t2、u2，如此往复。若X的秩是A，则有：

(12)

(13)

2 实验系统及污垢特性建模

2.1 实验系统及样本库

图1所示为实验所搭建的光管实验系统。管内流动的是通过向自来水中添加CaCl2和Na2CO3药品配制而成的析晶垢，硬度为800mg/L，在整个实验过程中通过化学滴定法保持硬度不变。实验光管外面是恒温水浴，由温控仪控制以实现水浴温度恒定(本实验水浴温度维持在40℃)。紧贴管壁安装有DS18B20、智能SCL-61D超声波流量计以测得壁温，出、入口温度测点和工质流量。实验工质由高位水箱流经实验管段时，在恒温水浴箱中进行换热，之后进入低位水箱。循环水被冷却后再由泵打到高位水箱，然后再进入实验管段，如此形成实验工质的循环。

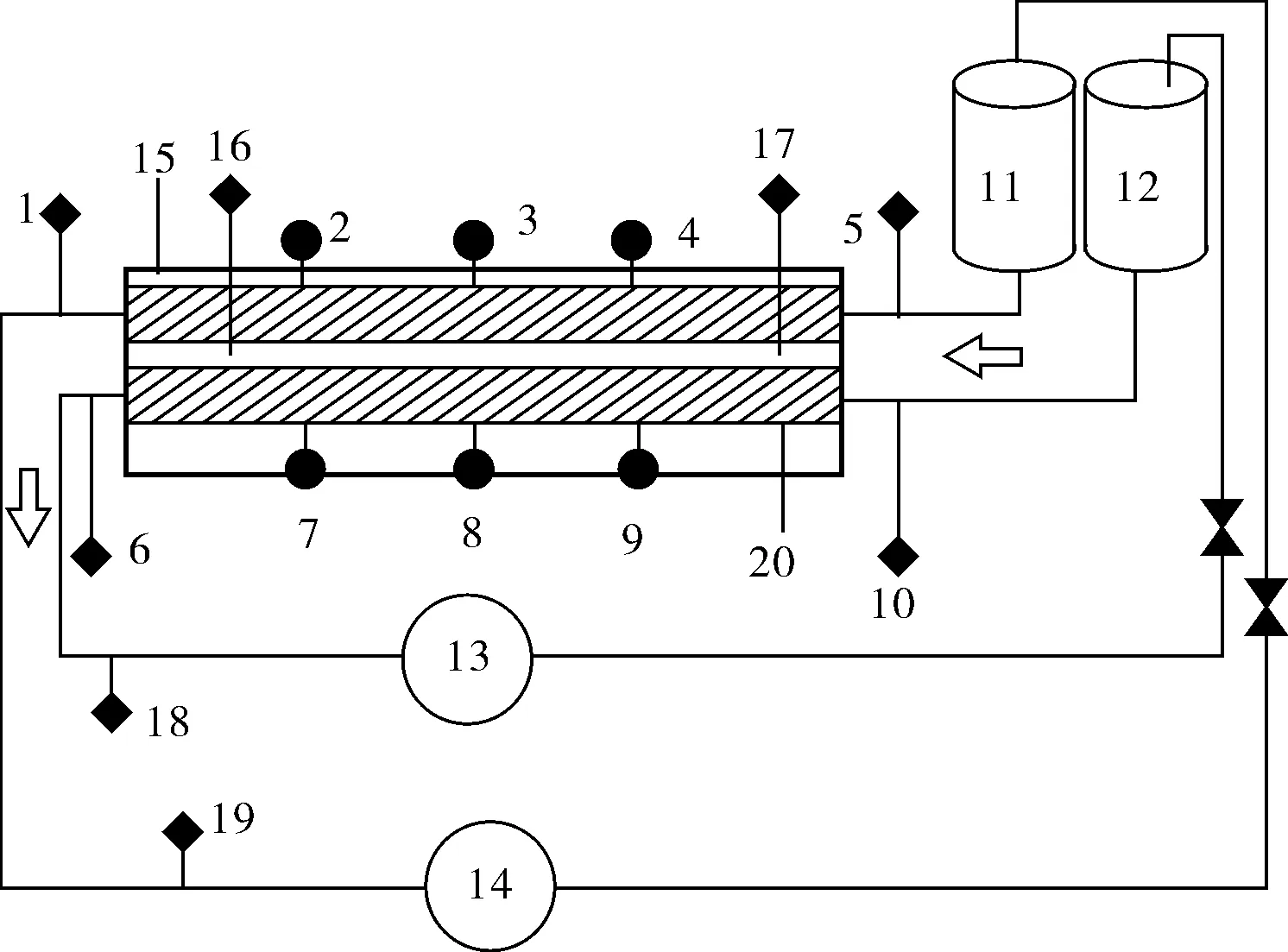
图1 光管实验系统

实验管为不锈钢光管，有效换热长度为2.235m，直径为0.011m，壁厚为1.5mm。由于管壁挂垢是一个相对较缓慢的过程，实验中通常每隔5～10min采集一次数据。实验共采集到历时50多个小时的130多组数据，取其中的60组作为训练样本，其余作为测试样本。

2.2 主成分的提取

对于本实验换热器，建立5个自变量1个因变量的污垢热阻偏最小二乘模型。具体主成分提取过程为：

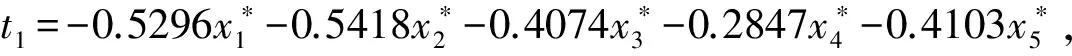
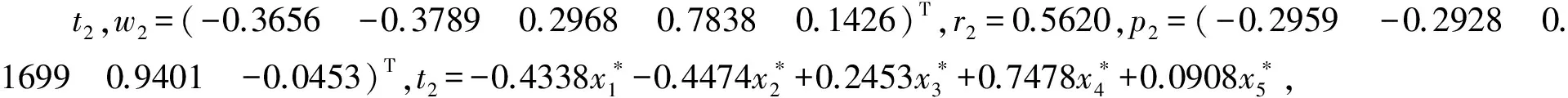
由此可知，当提取两个成分时，模型的预测能力最佳。因此可得标准化变量的回归方程为：

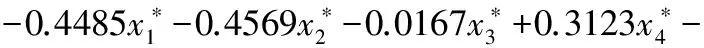
(21)

转换为原始变量的偏最小二乘回归方程为：

y=(-0.1050x1-0.1163x2-0.0191x3+0.2965x4-0.1807x5+10.1330)×10-4

(22)

2.3 模型预测结果

拟合方程的训练误差为3.06%。将测试样本输入训练好的拟合方程中，可得预测结果与实验结果的对比如图2所示，部分测试样本预测结果见表1。

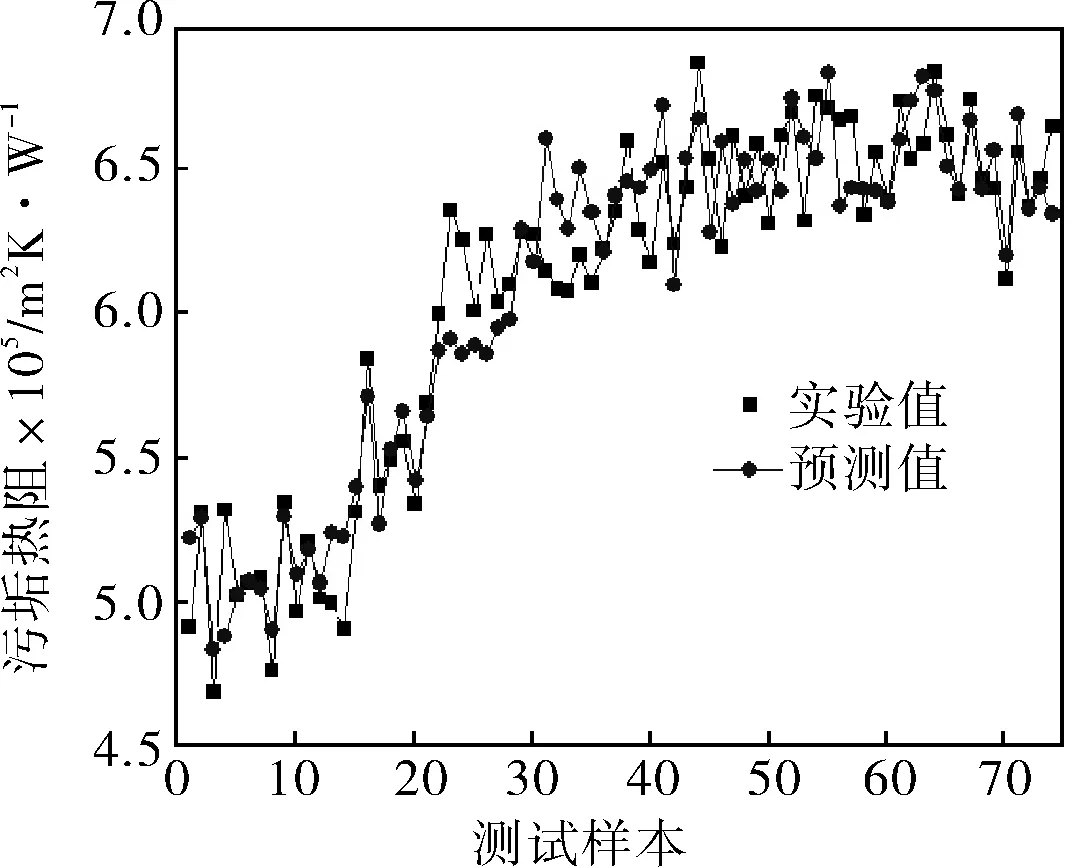
图2 测试样本污垢热阻随时间变化趋势

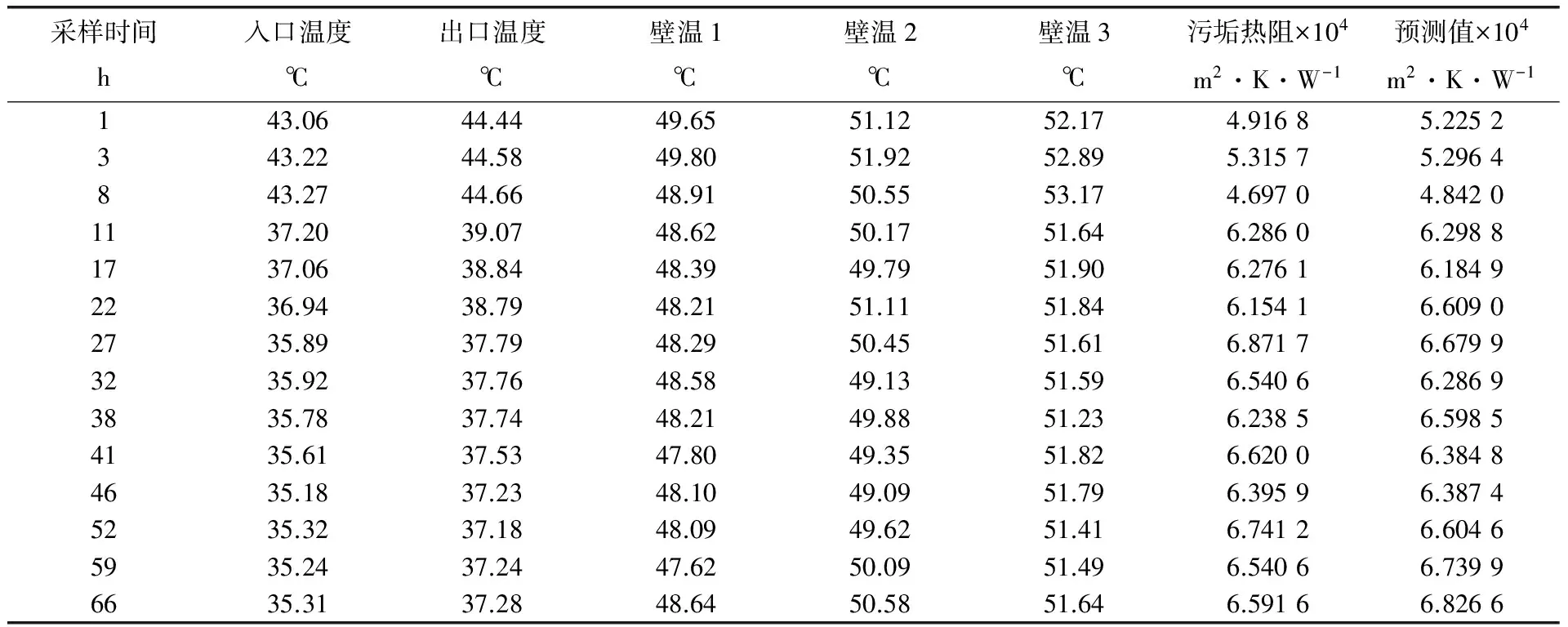
采样时间h入口温度℃出口温度℃壁温1℃壁温2℃壁温3℃污垢热阻×104m2·K·W-1预测值×104m2·K·W-1143．0644．4449．6551．1252．174．91685．2252343．2244．5849．8051．9252．895．31575．2964843．2744．6648．9150．5553．174．69704．84201137．2039．0748．6250．1751．646．28606．29881737．0638．8448．3949．7951．906．27616．18492236．9438．7948．2151．1151．846．15416．60902735．8937．7948．2950．4551．616．87176．67993235．9237．7648．5849．1351．596．54066．28693835．7837．7448．2149．8851．236．23856．59854135．6137．5347．8049．3551．826．62006．38484635．1837．2348．1049．0951．796．39596．38745235．3237．1848．0949．6251．416．74126．60465935．2437．2447．6250．0951．496．54066．73996635．3137．2848．6450．5851．646．59166．8266

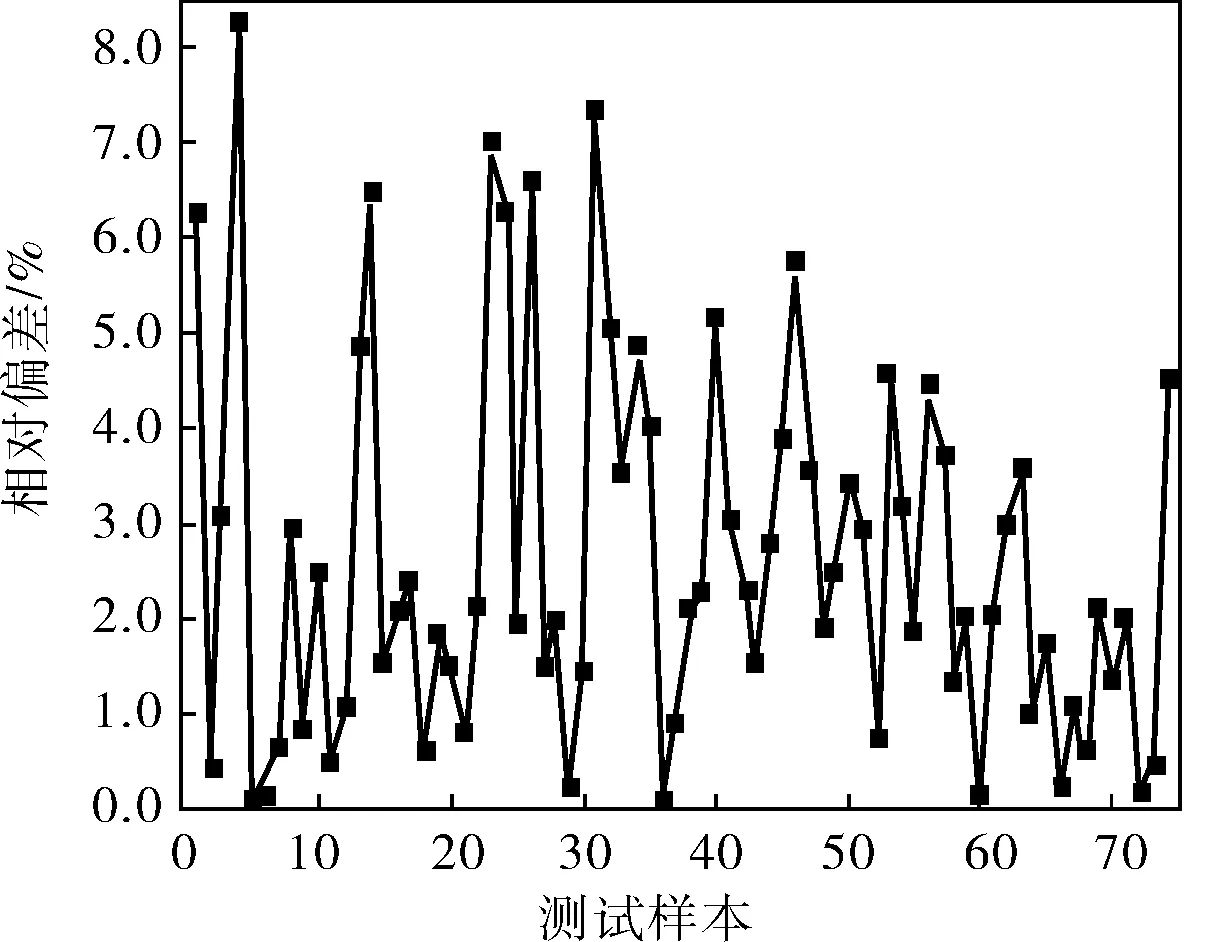
图3 测试样本相对偏差

由图3可知，计算得到的最大预测误差δ<8.50%。测试样本平均误差2.92%。相对误差较大的几组预测值主要集中于污垢的诱导期前后，究其原因：一方面此时参数的变化相对较大，从样本采集(包括训练样本和测试样本的采集，下同)角度则应该缩短采样时间间隔；而从刻画和描述事物特征角度，也需要尽量多的采集能确切描述光管污垢本质特征的样本，才能更全面、更细致、更准确地预测光管的污垢特性。

2.4 模型的验证

为了验证模型的预测能力，以另一运行周期的实验数据来检验该预测模型的预测精度，预测结果如图4所示，最大偏差为9.90%。

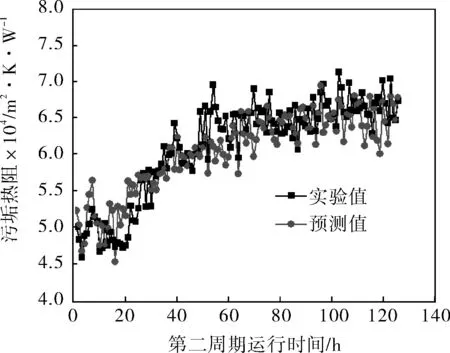
图4 第二周期污垢热阻随时间变化趋势

2.5 各自变量对预测模型的影响

2.5.1入口温度对预测模型的影响

为了分析入口变量对预测模型预测精度的影响，保持其余条件不变，忽略拟合方程的入口变量，仍然选取上述60组训练样本重新训练，提取主成分，以拟合PLS方程。

经过运算，Q3=0.3136>0.0975，Q4=-0.1318<0.0975，所以取3个主成分，由此，可得原始变量的偏最小二乘回归方程为：

y=(-0.2423x2+0.0823x3+0.1082x4+0.1562x5-

1.8134)×10-4

(23)

模型训练误差为3.05%。代入测试样本，得模型对测试样本最大误差为12.16%，平均相对误差为2.76%。

2.5.2出口温度对预测模型的影响

为了分析出口变量对预测模型预测精度的影响，保持其余条件不变，忽略拟合方程的入口变量，仍然选取上述60组训练样本重新训练，提取主成分，以拟合PLS方程。经过运算，Q3=0.2627>0.0975，Q4=-0.1341<0.0975，所以取3个主成分，由此，可得原始变量的偏最小二乘回归方程为：

y=(-0.2194x1+0.0718x3+0.1100x4+0.1315x5-

1.4127)×10-4

(24)

模型训练误差为3.13%。代入测试样本，得模型对测试样本最大误差为11.99%，平均相对误差为2.82%。

2.5.3壁温对预测模型的影响

为了分析3个壁温对预测模型预测精度的影响，保持其余条件不变，忽略拟合方程的壁温1(或2，或3)，仍然选取上述60组训练样本重新训练，提取主成分，以拟合PLS方程：经过运算，分别忽略3个壁温时，皆取两个主成分。模型训练误差为2.91%(忽略壁温2时为3.03%，忽略壁温3时为2.91%)。代入测试样本，得模型对测试样本最大误差为7.98%(忽略壁温2时为7.33%，忽略壁温3时为8.41%)，平均相对误差为2.78%(忽略壁温2时为2.66%，忽略壁温3时为2.75%)。

由以上讨论结果可知，在本实验条件下，忽略单一自变量时，皆减小了模型的训练误差，而当自变量取入口温度、出口温度、壁温1、壁温3时，模型对测试样本的预测精度最高，为2.66%。此时对测试样本的预测结果如图5所示。图6为该最优模型对第二运行周期的预测结果。

图5 四变量最优模型预测结果

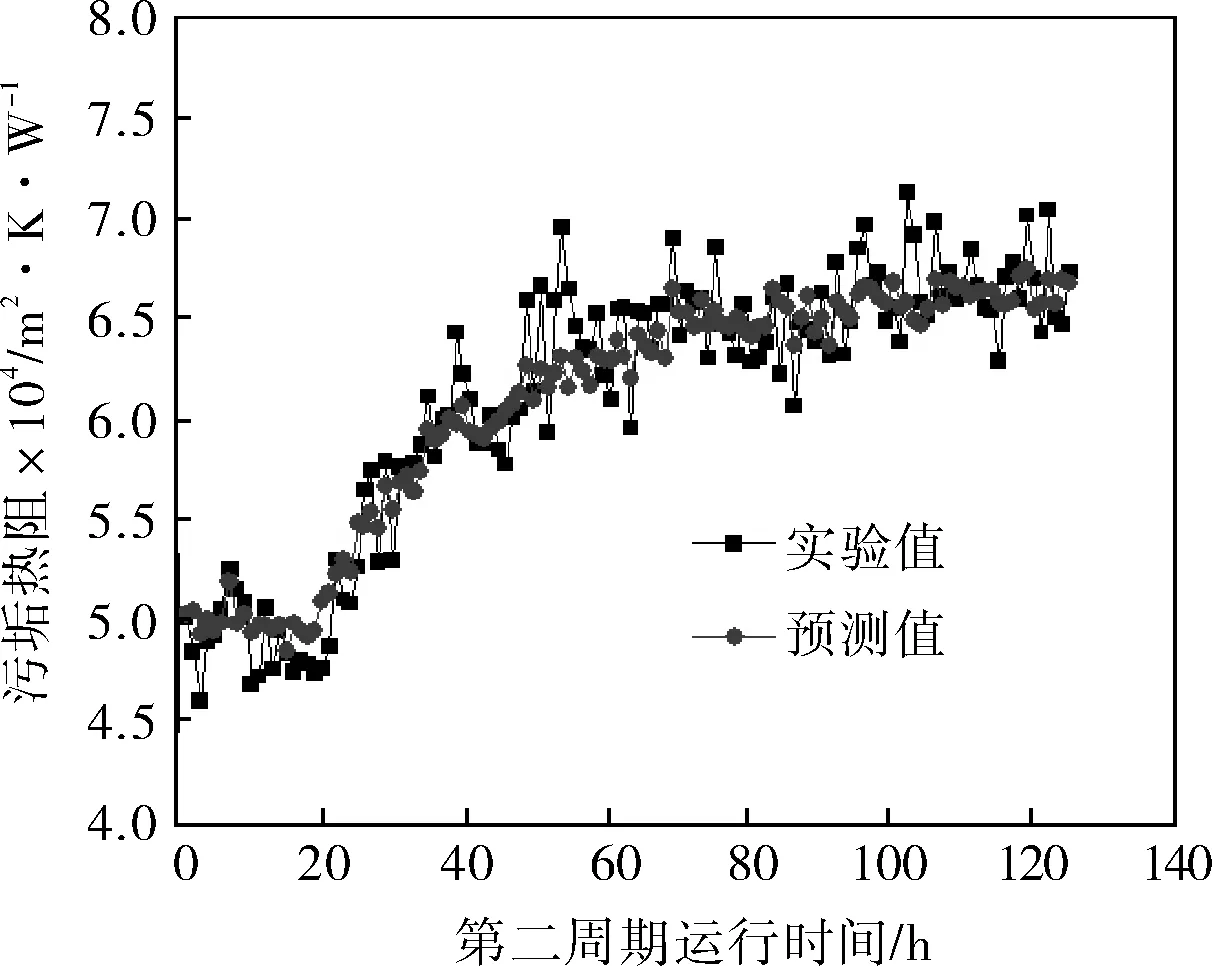
图6 第二周期污垢热阻随时间的变化趋势

此外，实验管的尺寸及材料等因素不影响本预测模型的结构；水浴温度对模型的影响相对较小，也可以不予考虑[38]。

3 结束语

笔者搭建了实验系统，测量并获得了壁温及出、入口温度参数值，并将其作为自变量，以光管换热器为主要研究对象，利用偏最小二乘算法建立了污垢特性预测模型。预测及验证结果表明，该预测模型预测偏差皆小于8.5%，满足工程实际要求，说明该方法所得污垢预测值能够较真实地反映光管实际污垢特性，为设计和运行人员今后在已知水质环境参数的条件下，提前预知换热器污垢特性以便为有效地防垢、抑垢提供了行之有效的方法。通过分析各单一自变量对预测模型的影响，得出了四变量优化预测模型，从而提高了模型的预测精度。此外，还分析了壁温等对预测模型的影响。

[1] McGuire J，Swartzel K R.Influence of Solid Surface Energies on Macromolecular Adsorption from Milk[C].American Institute of Chemical Engineers National Meeting. USA，1987：31.

[2] Müller-Steinhagen H，Zhao Q，Helali-Zadeh A，et al.The Effect of Surface Properties on CaSO4Scale Formation during Convective Heat Transfer and Subcooled Flow Boiling[J].Can J Chem Eng，2000，78(1)：12～20.

[3] Xu Z M，Yang S R.A New Predictive Model for Particulate Fouling[C]. International Conference on Understanding Heat Exchanger Fouling And Its Mitigation.New York：Begell House Inc，1997：115～122.

[4] 徐志明，杨善让.颗粒污垢剥蚀机制研究[J].工程热物理学报，1998，19(5)：612～615.

[5] Yang C F，Xu D Q，Shen Z Q.Study on the Scaling Rate Model of CaCO3in Saturated Water System[J].Chin J Chem Eng，1995，3(2)：139～144.

[6] Yang C F. Mechanisms of Calcium Carbonate Scaling During and Post Induction Period[C].Fouling Mitigation of Industrial Heat-exchange Equipment. New York：Begell House Inc，1995：275～286.

[7] Zubair S M，Sheikh A K，Budair M O，et al. Statistical Analysis of CaCO3Scaling in Heat Exchanger Tubes[C]. Fouling Mitigation of Industrial Heat-exchange Equipment. New York：Begell House Inc，1995：287～297.

[8] Zubair S M，Sheikh A K，Budair M O，et al. A Maintenance Strategy for Heat-Transfer Subject to Fouling：A Probalistic Approach[J]. ASME J Heat Transf，1997，119(3)：575～580.

[9] Zubair S M，Sheikh A K，Sultan K M，et al. A Simplified Probabilistic Cost Model for Maintenance of Heat Exchangers Subject to Fouling[C].Understanding Heat Exchanger Fouling and Its Mitigation.New York：Begell House Inc，1997：401～409.

[10] Somerscales E F C，Knudsen J G. Fouling of Heat Transfer Equipment[M]. New York：Hemisphere Publishing Corp，1981：31～53.

[11] Bott T R. Fouling of Heat Exchangers[M]. Amsterdam：Elsevier，1995：72.

[12] Bowen B D，Epstein N. Fine Particle Deposition in Smooth Parallel-Plate Channels[J].J Colloid Interface Sci，1979，72(1)：81～97.

[13] Vasák F，Bowen B D，Chen C Y，et al.Particle Deposition in Laminar and Turbulent Flows[J].Can J Chem Eng，1995，73(6)：785～792.

[14] Rodliffe R S，Means F A.Factors Governing Particulate Corrosion Product Adhesion to Surfaces in Water Reactor Coolant Circuits[R].UK：CEGB Report RD/B/N4525 Berkeley Nuclear Laboratories，1979.

[15] Epstein N. Particle Deposition and Its Mitigation[C].Understanding Heat Exchanger Fouling and Its Mitigation.New York：Begell House Inc，1997：3～21.

[16] Yang S R，Zhang H L，Xu Z M.Determination of Fouling Thermal Conductivity of Ash Layer on Heating Surface[C]. Heat Transfer 2002，Proceedings of the 12th International Heat Transfer Conference.France：2002：423～428.

[17] Yang S R，Xu Z M，Zhao X T. A Fractal Model For Thermal Conductivity in a Disperse System of Even Particulates[J]. Heat Transfer Asian Research，2000，29(7)：535～543.

[18] 赵晓彤，杨善让，徐志明. 粒径均匀散体热导率的分形描述[J].工程热物理学报，1999，20(4)：477～481.

[19] 张海林，杨善让，徐志明，等.提高重整化群精度的一个尝试[J].工程热物理学报，2003，24(6)：992～994.

[20] Yang S R，Zhang H L，Xu Z M，et al.Thermal Conductivity of Ash Layer Including Radiation Heat Transfer[C]. 3rd International Symposium on Heat Transfer Enhancement and Energy Conservation.Guangzhou：South China Univ Technology Press，2004：992～998.

[21] Crittenden B D，Kolaczkowski S T，Philips D Z.Chemical Reaction Fouling[C].Understanding Heat Exchanger Fouling and Its Mitigation.New York：Begell House Inc，1997：91～103.

[22] Fernandez-Torres M J，Fitzgerald A M，Paterson W R，et al. A Theoretical Study of Freezing Fouling Limiting Behavior Based on A Heat and Mass Transfer Analysis[J].Chemical Engineering and Processing，2001，40(4)：335～344.

[23] 徐志明，郭淑清，杨善让.基于概率分布的污垢模型[J].工程热物理学报，2003，24(2)：322～324.

[24] Kern D Q，Seaton R E. A Theoretical Analysis of Thermal Surface Fouling[J]. Chemical Engineering and Processing，1959，4(5)：258～262.

[25] Zubair S M，Sheikh A K，Shaik M N.A Probabilistic Approach to the Maintenance of Heat Transfer Equipment Subject to Fouling[J]. Energy，1992，17(8)：769～776.

[26] Xu Z M，Guo S Q，Yang S R，et al.Analytical Fouling Model Based on Probabilistic Approachi[J].Journal of Engineering Thermophysics，2003，24(2)：322～324.

[27] Fan S S.Gray Theory Based on Prediction for Condenser Fouling[J].Journal of Electric Power Science and Technology，2007，22(2)：12～15.

[28] Fan S S，Wang H N.The Prediction of Fouling in Condenser Based on T-S Model[J].Chinese Journal of Sensors and Actuators，2005，18(1)：123～128.

[29] Chai H D，Wang W H，Zhang L S.The Methods Study of Fouling Prediction Using Radial Basis Function Network[J]. Journal of Northeast Dianli University(Natural Science Edition)，2006，26(4)：46～49.

[30] 王建国，邸昊，何芳.电磁频率对污垢热阻及电导率的影响[J].化工自动化及仪表，2012，39(6)：761～764.

[31] 付亚荣，王开炳，王敬缺.神经网络用于油田地面集输管道结垢预测[J].西南石油学院学报，1999，21(2)：68～69.

[32] Enrique T，Cristóbal Cortés，Luis I D，et al. Monitoring and Prediction of Fouling in Coal-Fired Utility Boilers Using Neural Networks[J].Chemical Engineering Science，2000，60(18)：5035～5048.

[33] 侯迪波，杨丽明，周泽魁.基于模糊神经网络的周期性结垢预测方法研究[J].浙江大学学报，2004，38(3)：307～311.

[34] 樊绍胜，王耀南.基于T-S模型的冷凝器污垢预测[J].传感技术学报，2005，18(1)：123～128.

[35] 彭珍，张充，吴立锋，等.基于RBF神经网络的换热管污垢热阻预测[J].煤气与热力，2008，28(6)：26～28．

[36] 丁世飞，史忠植，靳奉祥.非线性迭代PLS信息模式识别算法[J].计算机工程，2008，4(1)：20～22.

[37] 文孝强，李国强，孙灵芳，等.基于偏最小二乘回归算法的燃煤碳元素分析[J].东北电力大学学报，2012，32(3)：31～36.

[38] 徐志明，杨善让，孙灵芳，等．波纹管污垢特性的试验研究[J].工程热物理学报，2001，22(4)：477～480.