一种车载小直角棱镜方位自动测量系统误差分析

王学根，孙 煜，贺永喜，姜 华

0 引 言

在火箭的方位瞄准系统中，直角棱镜作为惯性测量组合的方位敏感目标，固连在箭体上，地面瞄准设备通过对直角棱镜方位信息的测量，完成对火箭惯性测量组合的初始方位瞄准[1,2]。在车载情况下，火箭和瞄准设备都安装在一辆载车上，其相对位置大致不变，瞄准设备开机后数分钟内就能完成对箭上直角棱镜方位信息的测量，不再需要设备架设及其它人为操作，这种瞄准系统就是自动瞄准系统。在自动瞄准系统中，完成对直角棱镜方位角信息测量的设备通常为高精度自准直测角光管（简称“自准直光管”），其光电轴代表瞄准系统的基准方位，自准直光管测出箭上直角棱镜的方位信息，然后通过解算，确定箭上惯性测量组合直角棱镜法线的初始方位。

在上述自动瞄准系统中，直角棱镜固定在火箭上，虽然火箭与自准直光管等瞄准设备都安装在同一辆载车上，但直角棱镜和自准直光管的位置关系并不能认为保持不变。原因有以下几点：一是火箭和载车都不能认为是刚体，二是火箭相对载车要进行起竖和回收，它们之间还有相对运动及减震等环节，每次火箭回收到位后的位置不能完全一致。另外，为了缩短火箭测试准备时间，瞄准设备和箭上惯性测量组合都不进行精确调平，随载车停放位置的地面不水平度的不同，自准直光管与箭上直角棱镜也会有姿态的相对变化。为了适应箭上直角棱镜与自准直光管的位置相对变化并确保直角棱镜总能处于自准直光管的有效测量范围内，自准直光管的有效口径相对较大；另一方面，为了减少体积和重量，箭上直角棱镜越来越小。此种瞄准系统可以称为一种小目标直角棱镜及大口径自准直光管的方位自动测量系统。由于测量时自准直光管不重新架设、箭上直角棱镜不调平，其二者之间可能存在着姿态、位置变化等因素，分析小目标直角棱镜及自准直光管的姿态及位置变化对方位测量的影响，并对其可能带来的测量误差[3]采取针对性的控制措施，对提高自动测量系统的精度指标很有必要。由于位置变化引入的误差可以通过控制自准直光管与小目标棱镜的相对位置变化量进行抑制，因此本文对此项误差不再分析。

1 直角棱镜姿态对方位测量的影响

1.1 直角棱镜棱线水平时对方位测量的影响

1.1.1 直角棱镜棱线水平时的反射作用矩阵

图1为直角棱镜与自准直光管组成的自动测量系统示意。

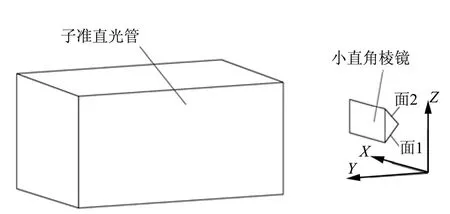
图1 直角棱镜与自准直光管组成的自动测量系统示意Fig.1 Auto-measuring System Composed of the Prism and Auto Collimating Light Pipe

如图 1所示，自准直光管和直角棱镜放置在图 1中右手螺旋坐标系中，直角棱镜的棱线与 X轴平行，则直角棱镜的两个反射面面1、面2法线的单位矢量N1、N2可分别表示为，

根据平面镜反射定律，平面镜的法线矢量为，其反射作用矩阵为R，则：

把1N、2N分别代入式（1），得直角棱镜反射面1的反射作用矩阵，直角棱镜反射面2的反射作用矩阵 R2，所以直角棱镜的反射作用矩阵为

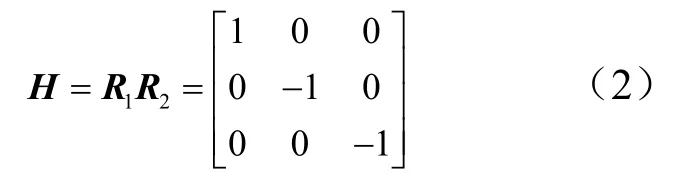
1.1.2 自准直光管水平测量时的影响

假设自准直光管呈水平状态对直角棱镜法线的方位进行测量，在图1的右手螺旋坐标系中，自准直光管测量光束的单位矢量可记为：，测量光束照射到直角棱镜并经过反射面面1、面2的反射，其返回的光束单位矢量为。

可见自准直光管的测量光束被直角棱镜原路返回，此种情况不会引入方位测量误差。

1.1.3 自准直光管倾斜测量时的影响

假设自准直光管与Y轴呈β角（β角的符号根据右手螺旋法则确定）对直角棱镜法线的方位进行测量，在图1所示的右手螺旋坐标系中，自准直光管的测量光束的单位矢量可记为：，测量光束照射到直角棱镜并经过反射面面1、面2的反射，则其返回光束的单位矢量为11′= =A HA

可见自准直光管的测量光束被直角棱镜原路返回，此种情况不会引入方位测量误差。

1.2 直角棱镜棱线倾斜对方位测量的影响

1.2.1 直角棱镜棱线倾斜θ角时的反射作用矩阵

直角棱镜棱线倾斜 θ角时，相当于直角棱镜绕 Y轴转动θ（θ角的符号根据右手螺旋法则确定）根据矢量绕Y轴转动θ角的转动公式[4,5]：

直角棱镜的反射面面1的法线矢量为=；直角棱镜的反射面面 2的法线矢量为

将、代入（1），得直角棱镜反射面面1、面2的反射作用矩阵分别为

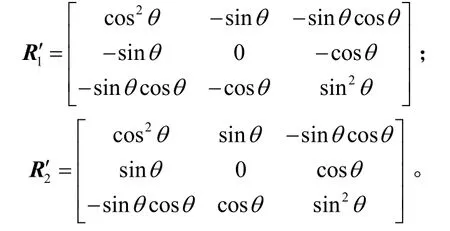
所以直角棱镜棱线倾斜θ时的作用矩阵为

1.2.2 自准直光管水平测量时的影响

自准直光管呈水平状态对直角棱镜法线的方位进行测量，自准直光管的测量光束单位矢量可以记为[6]，则测量光束经直角棱镜反射后，其返回光束的单位矢量为，可见自准直光管的测量光束被直角棱镜原路返回，此种情况不会引入方位测量误差。

1.2.3 自准直光管倾斜测量时的影响

同1.1.3节，自准直光管的测量光束单位矢量可记为，经直角棱镜反射后，其返回光束的单位矢量为。比较 A3与A3′，可见自准直光管测量光束被直角棱镜反射后不再原路返回。其在坐标系XY面内与Y轴之间的夹角为

在小角度情况下，2θ ≈sin(2θ)，tan(α)≈α，因此式（5）可简化为

式（6）即是直角棱镜棱线倾斜且自准直光管有俯仰角测量的工况下引入的方位测量误差，误差值大小与直角棱镜棱线的倾斜角θ、自准直光管的俯仰角的正切值tanβ成正比，误差值的正负号取决于直角棱镜棱线倾斜角θ的定义。

2 光管光轴不水平带来的方位影响

自准直光管随瞄准设备安置在载车上，在载车静止后，根据地面情况对载车横向进行大致调平，调平精度在5′以内，由于载车长、宽尺寸都比较大，其不能作为一个刚体看待。因此自准直光管总是存在俯仰和横滚两个方向不水平度的姿态，下面分别分析自准直光管俯仰和横滚两种不水平姿态对方位测量的影响。

2.1 自准直光管俯仰姿态对测量的影响

如图1所示的测量系统，自准直光管与Y轴成β角测量直角棱镜法线的方位时，自准直光管测量光束的单位矢量记为，直角棱镜棱线水平时的情况分析如1.1.3节；直角棱镜棱线有倾斜时的情况分析如1.2.3节。

2.2 自准直光管横滚姿态对测量的影响

自准直光管横滚工况是指自准直光管绕 Y轴有个小角度Ψ转动，此时自准直光管绕X轴存在有转动和无转动两种工况，下面分别进行分析。

2.2.1 自准直光管绕X轴无转动

自准直光管绕X轴无转动，仅绕Y轴有Ψ角（Ψ角的符号根据右手螺旋法则确定）转动，在自准直光管坐标系下其测量光束的单位矢量记为根据矢量转动式（3），矢量A5绕直角棱镜坐标系的 Y轴转动-Ψ角后，即转换到直角棱镜的XYZ坐标系，在XYZ坐标系下其单位矢量为，可见A5′与Y轴平行，其水平入射到直角棱镜。

a）直角棱镜棱线水平时。

直角棱镜的反射作用矩阵如式（2）所示，则 A5′经直角棱镜反射后的单位矢量为再经过矢量转动公式，变换到自准直光管坐标系下，在自准直光管坐标系下其单位矢量为，因此可得与A5方向相反，该工况不会引入方位测量误差。

b）直角棱镜棱线有θ角时。

直角棱镜的反射作用矩阵如式（4），则 A5′经直角棱镜反射后的单位矢量[7]为，再经过矢量转动式（3），变换到自准直光管坐标系下，在自准直光管坐标系下其单位矢量为 A5′ = Sy,ψA5′′=， 因 此 可 得 A5′′ 与A5方向相反，该工况不会引入方位测量误差。

2.2.2 自准直光管绕X轴转动β角

在该工况下，自准直光管即绕Y轴有Ψ角转动，又绕X轴有β角转动，Ψ角、β角的符号均根据右手螺旋法则确定。自准直光管测量光束的单位矢量在自准直光管坐标系下为[7]：

A6绕Y轴转动-Ψ角后，转换到小直角棱镜所在的XYZ坐标系后其单位矢量为

a）直角棱镜棱线水平时。

直角棱镜的反射作用矩阵如公式（2），则 A6′经直角棱镜反射后的单位矢量为， A6′′再经过矢量转动公式，变换到自准直光管坐标系下，在自准直光管其单位矢量为

A6′′与A6不再平行，此工况带来的方位测量误差为

在小角度情况下，2ψ ≈sin(2ψ)，tan(α)≈α，所以：

比较式（6）、式（7）可知，在自准直光管有俯仰角情况下，自准直光管横滚工况等效于直角棱镜棱线的相对倾斜工况，其引入的方位测量误差公式是一样的。

b）直角棱镜棱线倾斜θ角时。

直角棱镜的反射作用矩阵如式（4），则 A6′经直角棱镜反射后的单位矢量为

A6′′再经过矢量转动公式，变换到自准直光管坐标系下，在自准直光管坐标系其单位矢量[2]为

A6′′与A6不再平行，此工况带来的方位测量误差为在小角度情况下，2(θ +ψ )≈ s in2(θ +ψ)，tan(α)≈α，所以：

式（8）进一步证实：自准直光管横滚带来的方位测量误差等同于直角棱镜棱线倾斜带来的方位测量误差。由式（8）可知，在小角度情况下，自准直光管横滚及直角棱镜棱线倾斜引入的方位测量误差值大小，与直角棱镜棱线的倾斜角θ及自准直光管横滚角Ψ的代数和、自准直光管的俯仰角的正切值tanβ成正比。

3 结 论

在小角度情况下，自准直光管横滚带来的方位误差等效于直角棱镜棱线不水平时测量带来的方位测量误差，在自准直光管存在俯仰角测量时二者引入的方位测量误差公式是一致的。通过测量出直角棱镜的棱线不水平度、自准直光管的横滚角及俯仰角可以对这项误差进行精确补偿。如果直角棱镜的棱线不水平度无法给出，则自准直光管仰角要接近0°测量，才能消除该项方位测量误差。

[1] 王骏, 等. 一种直角棱镜棱脊相对变化量测量方法[J]. 科学技术与工程,2006, 6(18)： 2880-2886.

Wang Jun, et al. The measure of the right- angle prism axis's comparatively variety[J]. Science Technology and Engineering, 2006, 6(18)： 2880-2886.

[2] 李晓彤. 几何光学和光学设计[M]. 杭州： 浙江大学出版社, 1997.

Li Xiaotong. Geometric optics and design[M]. HangZhou： Zhejiang University press, 1997.

[3] 郭贺, 等. 棱脊大角度倾斜下的瞄准误差分析[J]. 红外与激光工程,2011, 40(1)： 138-142.

Guo He, et al. Influence of prism with large-angle tilt on aiming accuracy[J]. Infrared and Laser Engineering ,2011, 40(1)： 138-142.

[4] 赵军丽, 等. 直角棱镜棱脊不平度的检测方法[J]. 红外与激光工程,2013, 42(1)： 228-232.

Zhao Junli, et al. Detecting method of right-angled prism tilting[J]. Infrared and Laser Engineering ,2013, 42(1)： 228-232.

[5] 王骏, 等. 直角棱镜系统反射面平行度误差的补偿方法[J]. 科学技术与工程, 2007, 7(20)： 5351-5354.

Wang Jun, et al. Compensate method of right-angle prism system reflect surface parallelism error[J]. Science Technology and Engineering,2007,7(20)： 5351-5354.

[6] 张俊杰, 等. 直角棱镜用作自准直反光镜的光学特性[J]. 宇航计测技术,2009, 29(4)： 1-3, 21.

Zhang Junjie, et al. The optica1 characteristics of ritht angle prisms as auto collimating mirror[J]. Journal of Astronautic Metrology and Measurunent,2009, 29(4)： 1-21.

[7] 王大鹏, 等. 等腰直角棱镜反射方程的推导及其在瞄准中的应用[J].应用光学, 2005, 26(3)： 41-44.

Wang Dapeng, et al. The derivation of the isosceles right-angle prism 's reflection equation and its application to aiming[J]. Applied Optics , 2005,26(3)： 41-44.