固液两相叶片圆盘泵蜗壳内流动数值模拟*

周昌静 陈国明 谭海东

(1.中国石油大学 a.化学工程学院；b.海洋油气装备与安全技术研究中心；2.长春工业大学机电工程学院)

叶片圆盘泵由于叶轮叶片的轴向不连续，使其无堵塞、性能好，叶轮受磨损程度小，作为一种新型泵，目前越来越多的应用于市政、石油、化工、采矿及冶金等行业的难以实现泵送的场合，用于输送含有固体颗粒的固液两相或多相介质[1，2]。由于其叶轮结构的特殊性和输送介质的多样性，固液两相叶片圆盘泵内部的流动极其复杂。文献[3]根据叶片圆盘泵叶轮存在无叶区的特点通过泵内固液两相的流动模拟，对叶轮内固液两相流动规律和颗粒分布规律进行了分析。但对叶片圆盘泵蜗壳内的固液两相流动规律，还未见到有关的文献报道。蜗壳作为泵的重要过流部件，其设计不合理常常会导致泵的运行效率低、叶轮所受径向力大和局部磨损严重，造成能源和材料浪费[4，5]。笔者以一个固液两相叶片圆盘泵为研究对象，对其内部流动进行固液两相工况下的数值模拟，将其内部流动可视化，得到了蜗壳内的速度、压力和固相体积分数分布，并根据叶片圆盘泵的叶轮结构特点对蜗壳流道内的流动特征进行研究，为更好地实现叶片圆盘泵叶轮与蜗壳的匹配设计打下基础。

1 叶片圆盘内固液两相流动的模拟

1.1 模型建立和网格划分

数值计算所用模型泵叶轮结构如图1所示，特点是叶片在轴向不连续，流道较一般的离心泵要宽。叶轮外径200mm，盘间距36mm，叶片高度13mm，采用环形蜗壳结构。根据叶片圆盘泵叶轮叶片轴向不连续的特点，将叶轮无叶区和叶片区内流动计算域分别建模，计算区域和网格如图2所示。

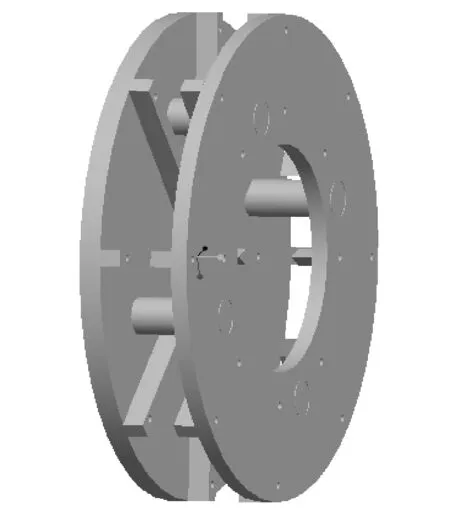
图1 圆盘泵叶轮

1.2 边界条件

基于文献[3]关于叶片圆盘泵内固液两相流动所作的假设，将单相流动的标准k-ε湍流模型扩展至多相湍流模型，将单相流的压力速度耦合SIMPLEC算法扩展至多相流动中[6]，可对叶片圆盘泵内的固液两相流动进行数值模拟。

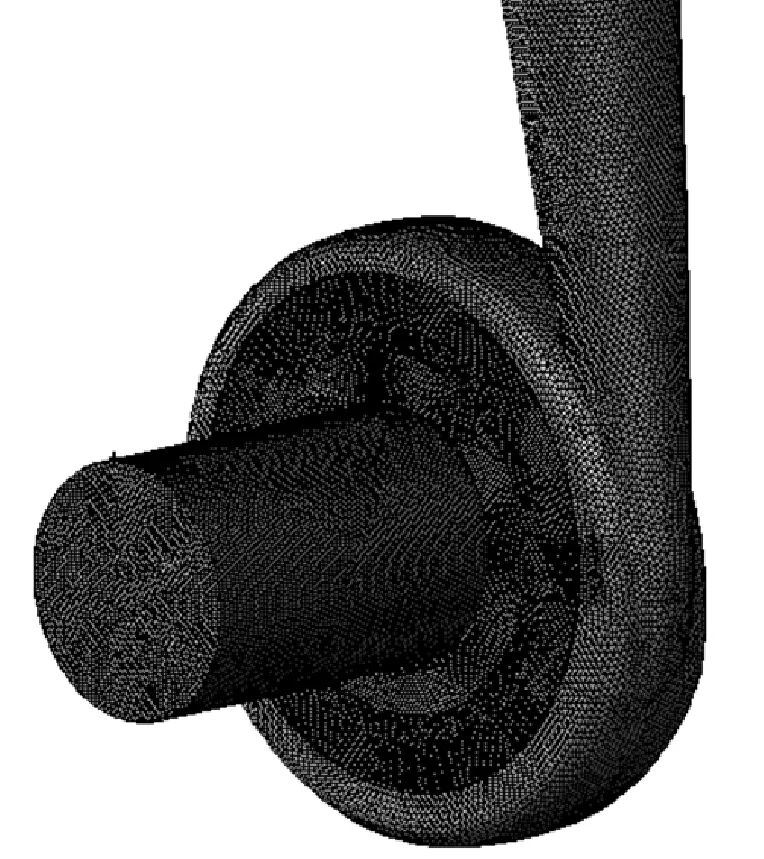
图2 计算区域和网格

泵的进口采用稳态、均相、轴向速度恒定的速度进口条件，由质量守恒定律和进口无预旋的假设确定轴向速度，这里假定固液两相在入口有相同的速度，同时假定进口截面浓度分布相同，给定来流速度、湍动能和耗散率的预估值。流道内过流壁面上均采用无滑移壁面条件，采用标准壁面函数模拟近壁面的流动。泵的出口采用自由出流条件。

2 计算结果及分析

以粒径为0.25mm、固相体积分数为10%的工况为例，对叶片圆盘泵蜗壳内速度、压力和颗粒固相体积分数分布规律进行分析。针对叶片圆盘泵叶轮不连续的特点，分别对叶轮无叶区和叶片区内作出轴截面，z0表示叶轮中间截面，即无叶区中间截面，z0.5和z-0.5分别表示进口侧从动盘和轮毂侧主动盘叶片区中间轴截面(1/2叶高)，图3为轴截面示意图。

2.1 蜗壳轴截面内速度分析

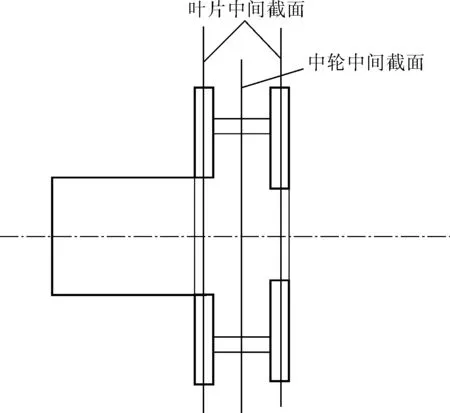
图3 分析截面示意图

图4为蜗壳内3个轴截面内速度分布，可以看出，叶片区和无叶区所对应轴截面蜗壳内速度明显不同，蜗壳中间截面内速度明显低于叶片区所对截面内速度，关于中间截面对称的叶片区两截面所对应的蜗壳内速度分布基本一致，这与文献[7]根据叶片圆盘泵叶轮内叶片区和无叶区速度分布所分析的叶片圆盘泵工作机理相一致，即叶轮内无叶区流体是在叶片区流体带动下混合流入蜗壳的，所以蜗壳内无叶区所对应截面内速度要小于叶片区所对截面速度。3个截面内沿径向速度梯度明显，速度随蜗壳半径增大而减小；在靠近隔舌处存在低速区，特别是叶片区所对应截面内速度变化明显，在蜗壳靠近扩散管出口区域存在高速区，这可能是由于在这两处截面设计不合理、面积变化不均造成的，同时扩散管内速度在扩散管隔舌侧近壁面部分区域存在明显的低速区，分析是扩散角与叶片圆盘泵叶轮不匹配造成的。

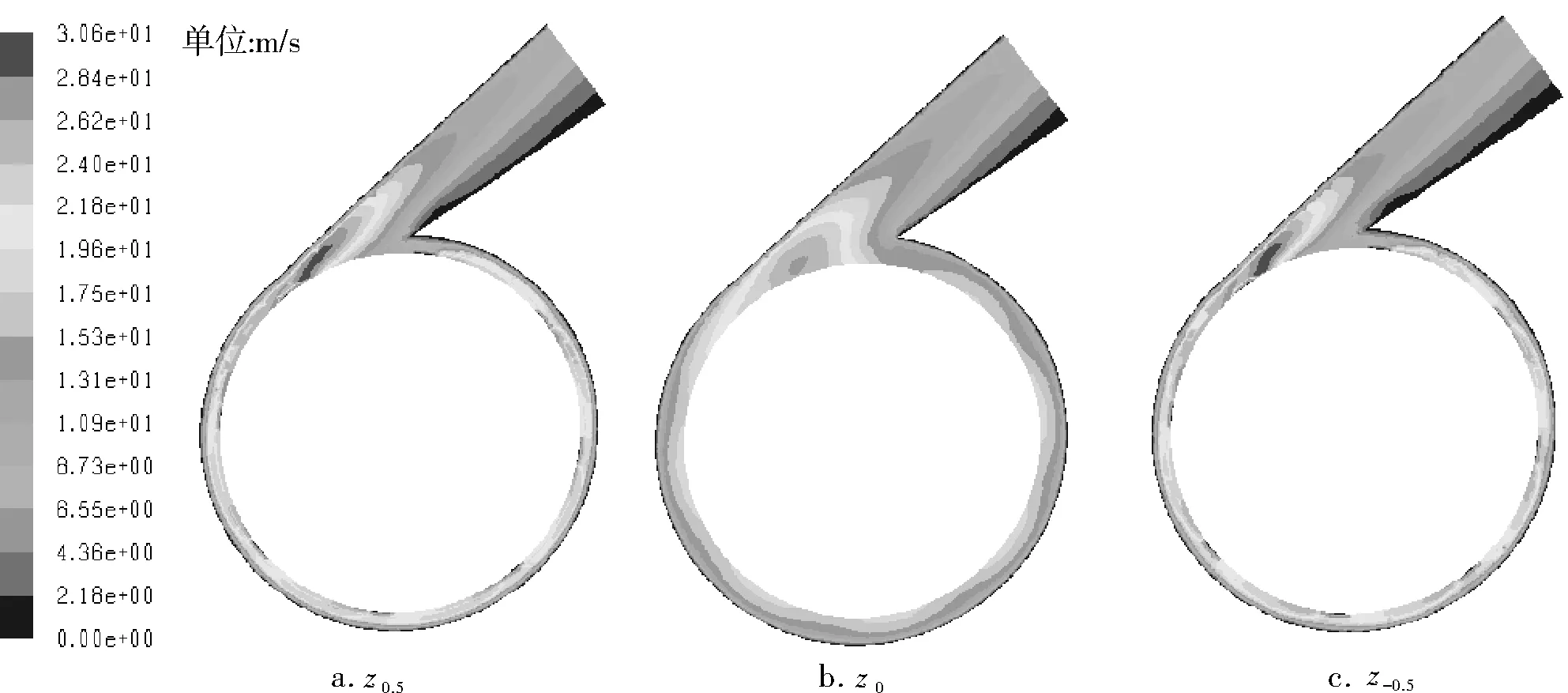
图4 蜗壳轴截面速度分布

2.2 蜗壳轴截面内压力分析

从图5蜗壳中3个轴截面的压力分布可以看出，无叶区和叶片区所对应的轴截面蜗壳内压力变化不大，这与文献[7]所得到的叶轮内接近叶轮出口无叶区和叶片区压力差别不大的结论是一致的。随着蜗壳半径的增大压力基本上呈不断增加，从隔舌开始沿顺时针方向压力也不断增加，在蜗壳扩散管段压力不断升高，说明蜗壳扩散管段起到了降速扩压的效果。在靠近隔舌和扩散管处存在局部的低压区，这与图4中的速度分布相对应。

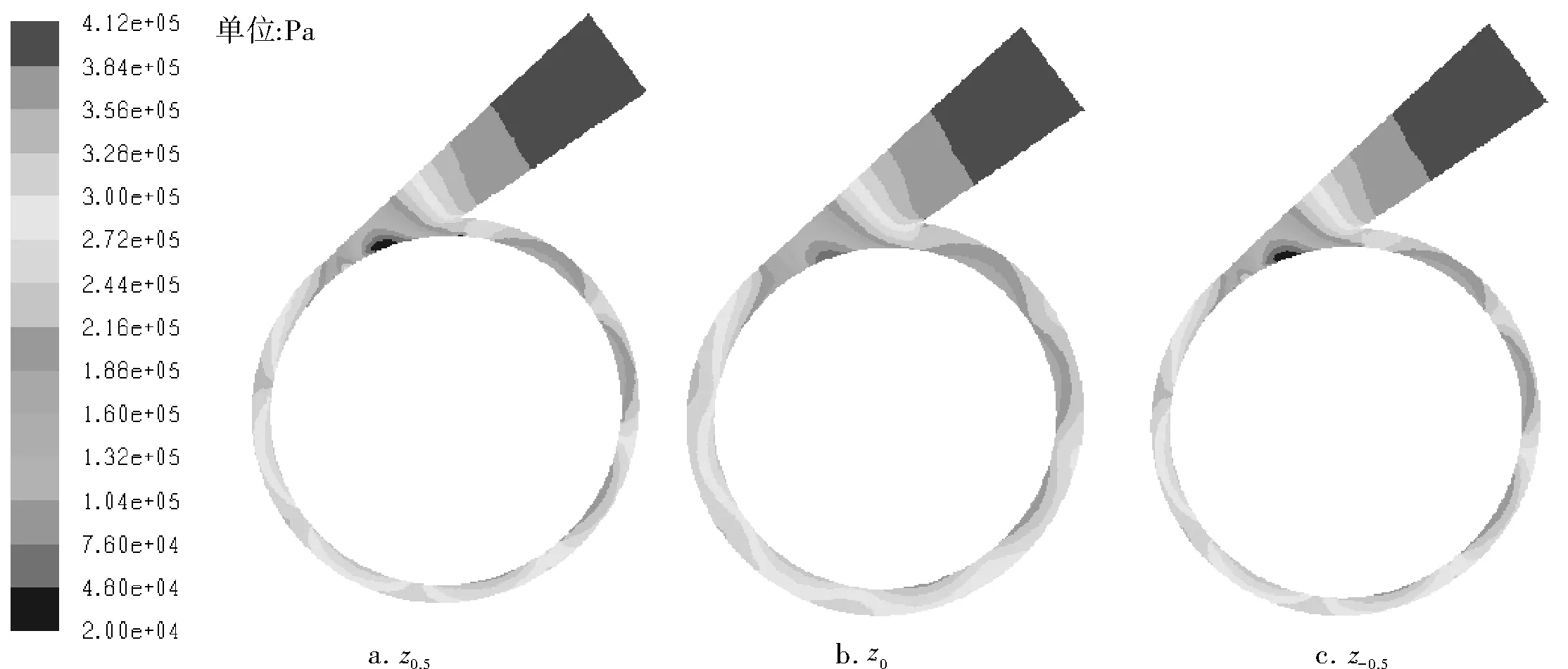
图5 蜗壳轴截面压力分布

2.3 蜗壳轴截面内固相体积分数分析

图6为蜗壳内固相体积分数的分布，可以看出，与叶轮无叶区相对应的蜗壳截面内固相体积分数要远远大于叶片区所对应的截面内固相体积分数，这与图7所示的叶轮内内颗粒分布相关。由图7可以看到叶轮内无叶区的固相体积分数远远大于叶片区内的固相体积分数，说明叶轮内固相颗粒主要经无叶区内流出进入蜗壳，导致蜗壳与叶轮无叶区相对应轴截面内颗粒体积分数大于叶轮叶片区所对应截面内体积分数。径向上颗粒体积分数沿蜗壳也存在梯度，越靠近蜗壳流道壁颗粒浓度越高，这与蜗壳内的速度分布相关，如前面分析的与无叶区相对应部分的流体速度和靠近流道壁处流体速度相对较小，因而固相颗粒受液相带动的影响较小，所以在与无叶区所对应的的蜗壳壁面附近固相体积分数最大。

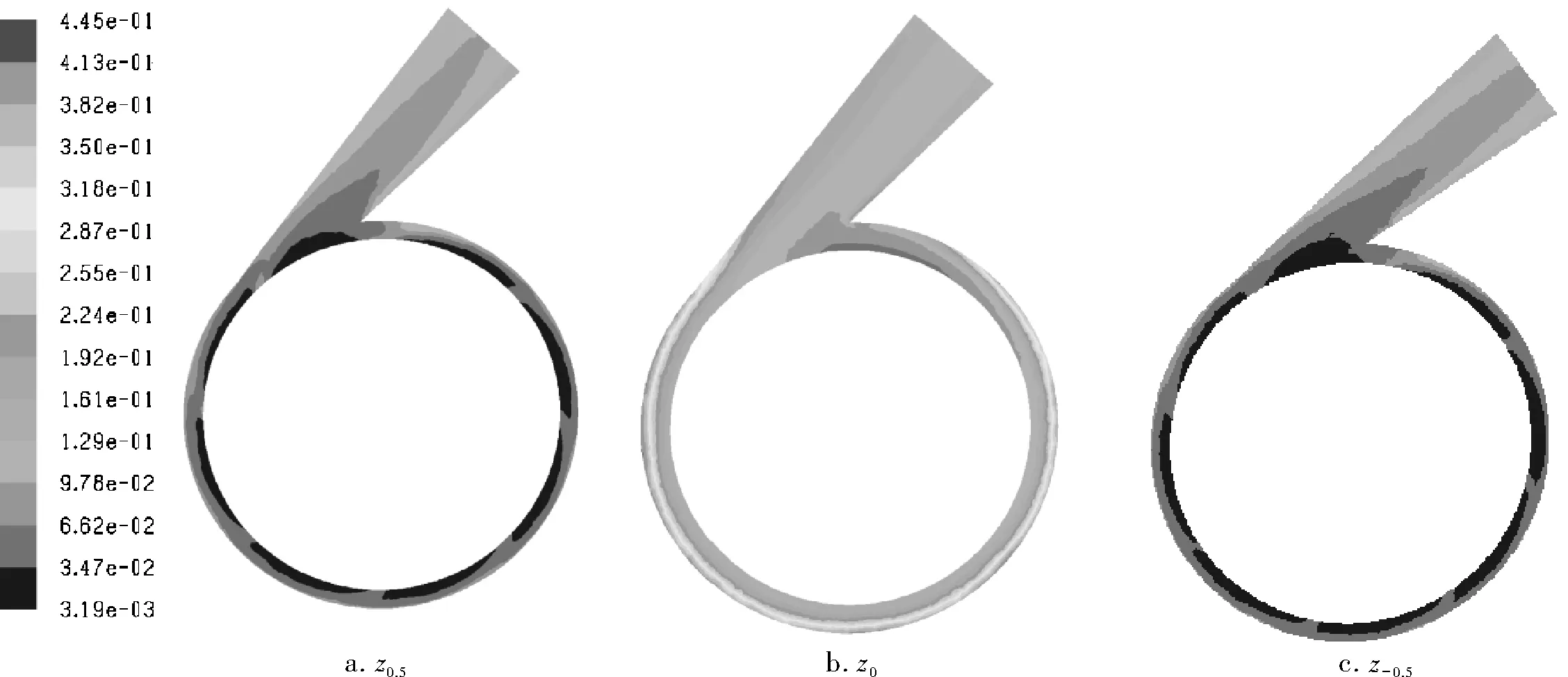
图6 蜗壳轴截面固相体积分数分布

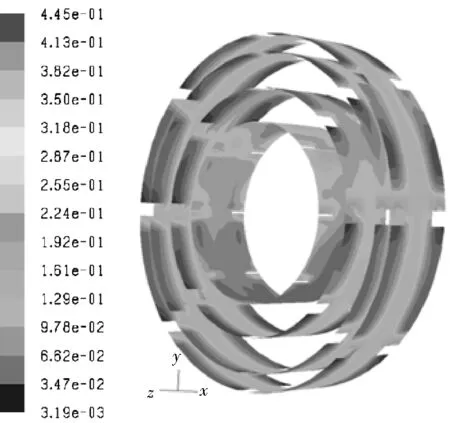
图7 叶轮内不同半径环接截面固相体积分数分布

3 结束语

通过对叶片圆盘泵内固液两相流动的数值计算，实现了叶片圆盘泵蜗壳内流动模拟，根据叶片圆盘泵叶轮存在无叶区的特点，分析得到蜗壳内叶轮叶片区和无叶区所对应轴截面内部流动特征，同时根据蜗壳内流动发现蜗壳中存在设计不合理截面。为后续叶片圆盘泵与不同蜗壳的匹配、蜗壳内流动的进一步分析打下基础，对叶片圆盘泵的性能优化具有重要参考价值。

参考文献

[1] Max I，Gurth. Rotary Disc Pump[P]. United States Patent: 7097416 B2, 20060829.

[2] Benson S, Pacello J.Solving the Problems of Pumping Medium-to-high Density Paper Stock[J]. World Pumps，1997，368：68～71.

[3] 周昌静,陈国明, 徐长航. 叶片圆盘泵固液两相流动规律数值模拟[J].中国石油大学学报(自然科学版), 2010, 34(5): 147～151, 158.

[4] Guo P C, Luo X Q, Zhou P. Numerical Investigation of Different Volutes in a Low Specific Speed Centrifugal Pump[C].2009 ASME Fluids Engineering Division Summer Meeting. Colonado: 2009.

[5] 张兄文, 李国君. 离心泵蜗壳内部非定常流动的数值模拟[J]. 农业机械学报, 2006, 37(6): 63～68.

[6] 福军.计算流体动力学分析[M]．北京：清华大学出版社，2007：128～131．

[7] 周昌静, 陈国明, 徐群, 等. 圆盘泵流动规律研究[J]. 流体机械, 2010, 38(10): 44～47.