一种基于雷达导引头的弹道导弹爆高解算方法

郑宗贵 王继平 林红斌 解 静



一种基于雷达导引头的弹道导弹爆高解算方法

郑宗贵①王继平*①②林红斌①解 静①

①(第二炮兵装备研究院 北京 100085)②(96271部队 洛阳 471000)

目前弹道导弹主要通过无线电引信测高来进行战斗部爆高控制，但弹头的再入环境对无线电引信测高装置的要求非常高，且引信存在着易被干扰的问题。为此，该文针对采用雷达景象匹配末制导的弹道导弹，提出一种基于雷达导引头的弹道导弹爆高控制方法，通过雷达导引头测高数据与惯性导航数据的融合处理，实时计算弹头飞行高程，来实现爆高控制，既保证了精度，又增强了抗干扰能力。仿真算例证明了该方法的有效性和爆高解算精度。

雷达导引头；弹道导弹；爆高

1 引言

近些年出现了一些新的测高设备与方法。点头式测高雷达容易受到欺骗[10]；机载预警雷达测高精度易受地-海杂波、大气折射、电波传播多径效应等因素影响[11]；InSAR系统高程测量受信噪比、体散射、时间去相干等非理想因素的影响[12]；杜晓辉等人[13,14]提出利用已发展完备的地面移动通信基站作为气压差分测量基准点的差分气压测高方法，虽然精度高，但移动通信基站易受干扰，这些测高设备或方法均不适合在弹道导弹上使用。针对采用景象匹配末制导的弹道导弹，温求遒等人[15]提出了利用图像导引头角量测信息进行弹目相对距离估计，还未用于爆高的控制；苏昂[8]提出了单帧多点匹配和帧间单点匹配测高方法，但是该方法限制在景象匹配区测高，不适用于爆高的控制。为此，本文提出了一种基于雷达导引头的弹道导弹爆高解算方法，利用雷达导引头测高数据，与惯性导航数据进行融合处理，实时计算出满足战斗部爆高精度要求的高程，既能增强抗干扰能力[16]，又能保证精度。

由于弹道导弹惯导工具误差的存在，其导航误差会随着工作时间逐渐增大，由导航定位数据确定导弹飞行中的高程，很难满足爆高精度要求。然而对于采用雷达景象匹配末制导导弹，其给出的雷达某一时间间隔的连续测高数据，精度非常高，可将该数据和惯性导航高程解算数据进行融合处理，实时计算高程以满足爆高控制精度要求。

雷达景象匹配导引头测高时，所得的测高数据是雷达导引头天线相对地面的高程，而爆高数据要求的是弹头质心相对目标点的高程，因而，需要将雷达导引头的测高数据由相对天线位置转换到相对弹头质心位置。另外，由于惯性导航数据是相对于惯组的安装位置，将雷达数据与惯性导航高程解算数据融合时，需将惯性导航数据转换到相对于弹头的质心位置。

综上所述，基于雷达导引头的弹道导弹爆高解算思路是首先将惯性导航数据转换到相对于导弹弹头的质心位置，并解算对地高程；接着将景象匹配雷达最后一次成像后的连续测高数据转换到导弹质心位置；然后将两者之差(即惯导解算高程误差值)拟合成时间的函数，根据导弹飞行时间，修正惯导解算高程误差，获得高精度的高程，满足爆高控制精度要求。

2 基于雷达导引头的爆高解算方法

首先，给出惯组安装位置偏离弹头质心引起的速度位置偏差模型和雷达导引头天线位置偏离弹头质心引起的高程偏差模型；在此基础上给出两者的数据融合模型及爆高解算方法。

2.1惯测组合安装位置偏离弹头质心引起的速度位置偏差模型

一般情况下，弹载惯性测量装置安装在导弹仪器舱内，安装位置与弹头质心不重合，因此再入段加速度表测量的视加速度为相对安装位置处的值，与相对质心处的值存在差异。然而，爆高控制是按弹头质心运动的高程进行控制，因而需将加速度表测量的视加速度归算到质心，再计算弹头的质心运动。

2.1.1基本假设 为便于将加速度表测量的视加速度归算到质心，作如下基本假设：

(1)忽略弹头飞行时的动态过程，即满足瞬时平衡假设；

(2)在标准条件下飞行，不计各种干扰对测量装置输出信号的影响；

(3)忽略弹头的弹性振动。

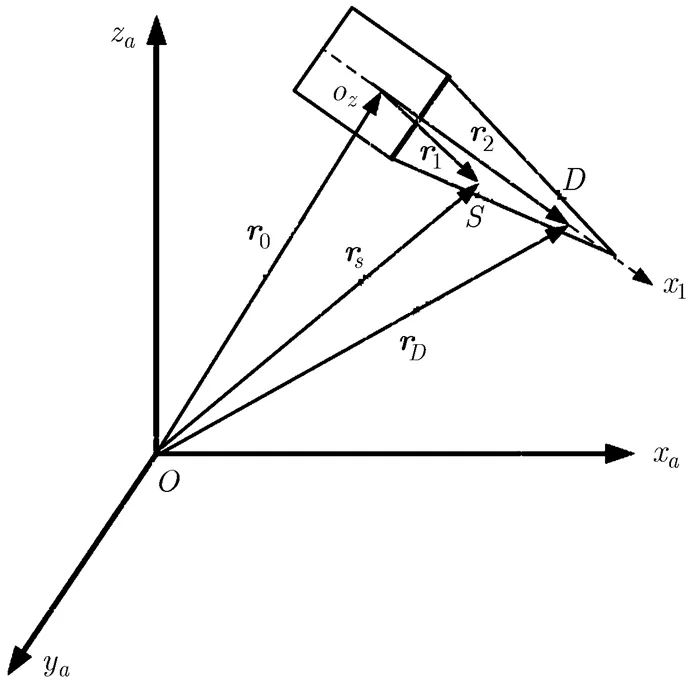
图1 惯组测量装置安装偏差矢量图

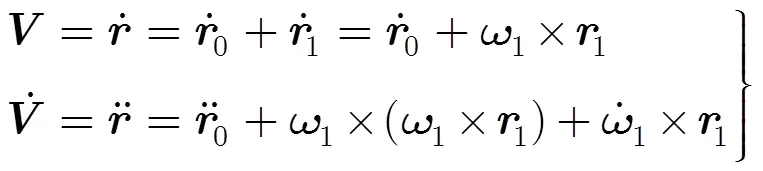
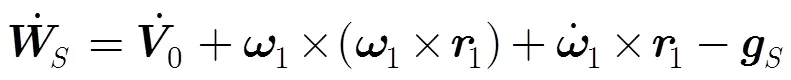
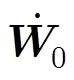
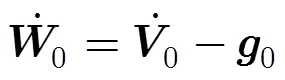
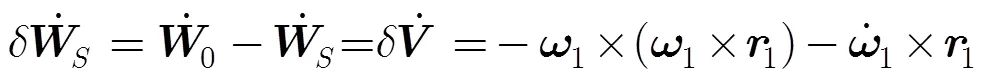
令

根据弹体坐标系与惯性坐标系间的关系矩阵，可得惯测装置偏离质心安装时的视加速度偏差在惯性坐标系各轴上的分量式为

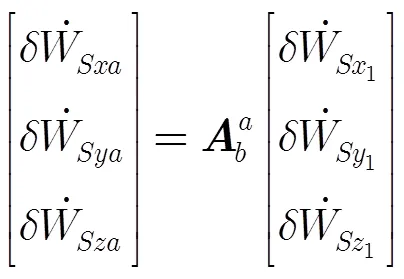
弹头质心视加速度为

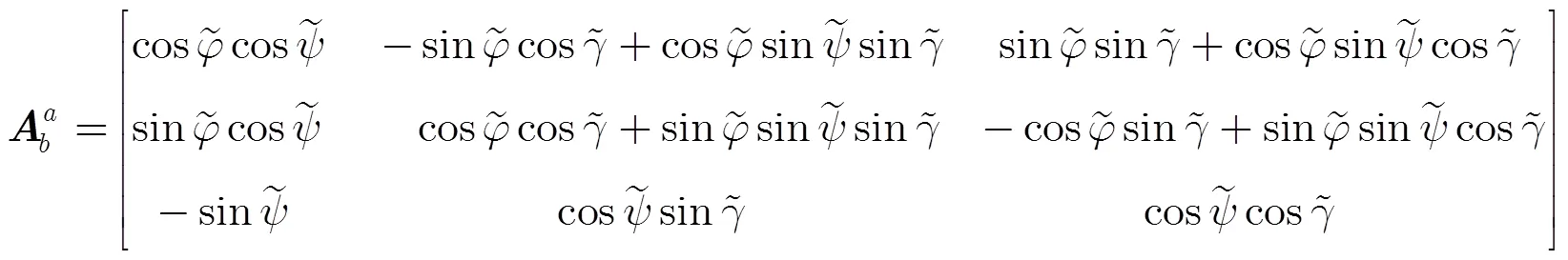
用式(8)修正惯测视速度增量，并代入弹头导航计算式(9)，可计算弹头质心的速度和位置。

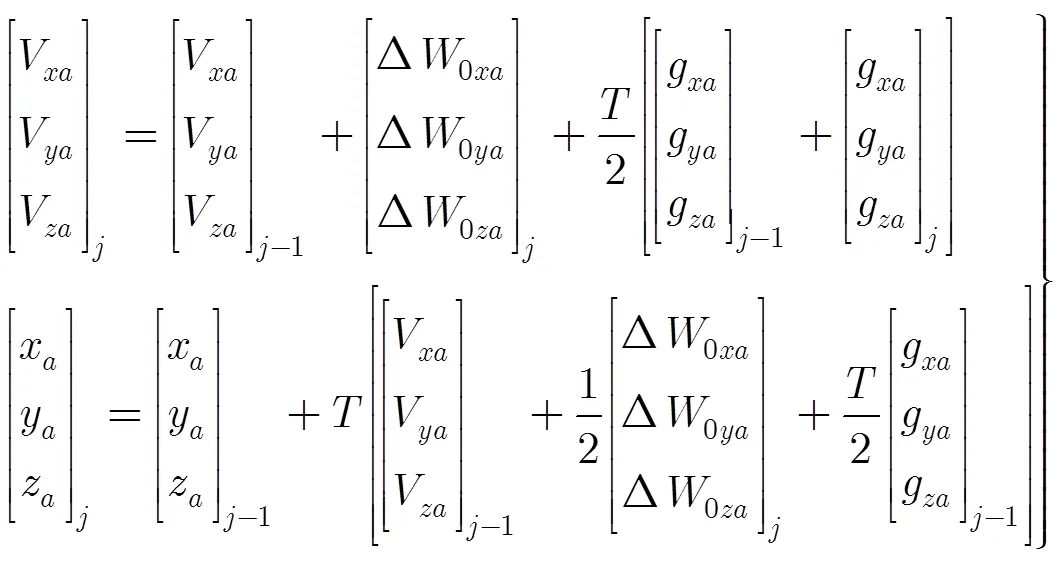
式中

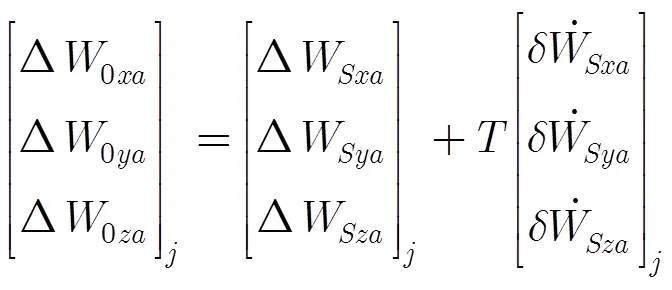
2.2 雷达天线偏离弹头质心引起的高程偏差模型

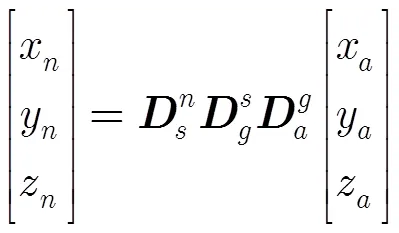
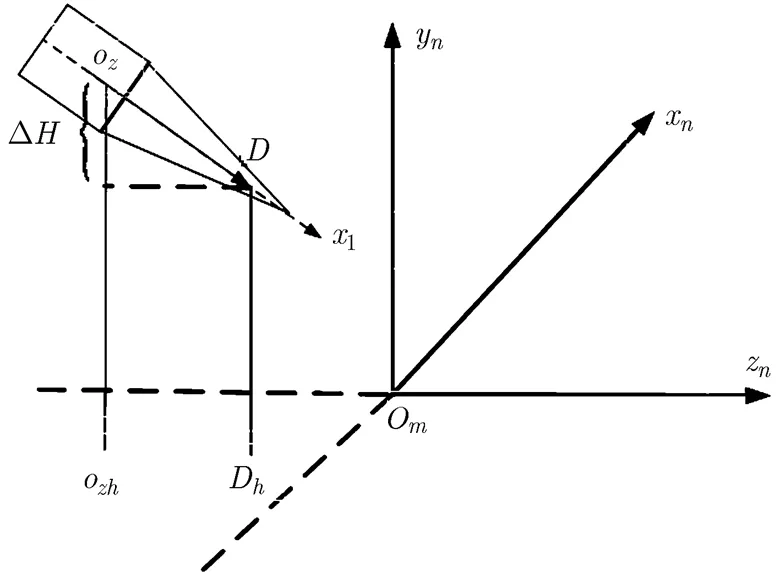
图2 目标坐标系

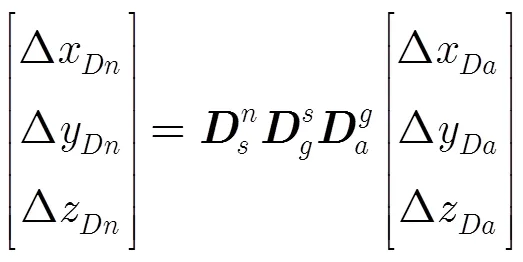
高程偏差为

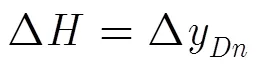
2.3 高精度爆高解算方法

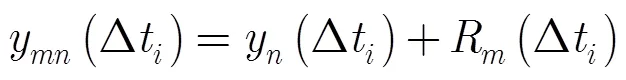
雷达测高方程为

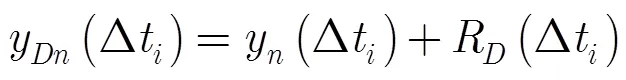
若目标区平坦，雷达天线对地高可近似为对目标点高；若已知目标区地形高程数据，可根据惯导数据计算弹头经纬坐标，插值获取当前地形高程值，将雷达对地高归算到雷达对目标点高。则雷达测高与惯性导航计算高之差为

令

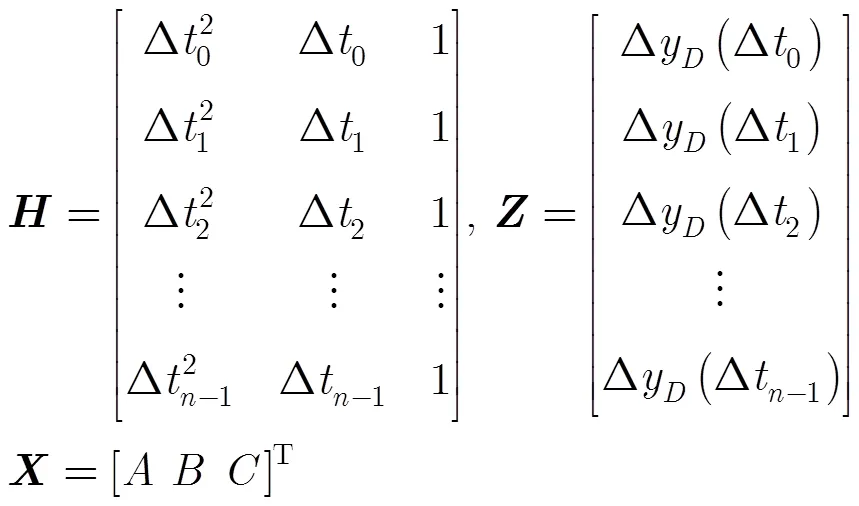
3 引爆时间预报

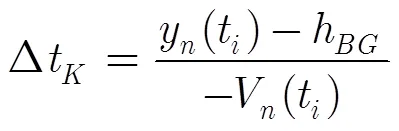
4 仿真算例

为了验证本文爆高解算方法的有效性，分别在地形平坦区和地形起伏区，采用最小二乘二阶滤波模型，进行爆高解算。

4.1 仿真条件

对标准弹道添加不同的速度误差和位置误差，形成500条惯组测量误差弹道，进行爆高解算精度仿真计算。

4.2 仿真结果

针对图3的目标区平坦地形情况，最小二乘滤波解算爆高仿真结果如图4，图5所示。

由仿真结果可以看出：滤波前后，测高误差均值差异不大，都约为0 m；滤波后测高误差标准差约为1.2 m，而单点测高的标准差约为2.2 m，可见滤波后，测高精度提高。

针对图6的目标区地形起伏区域情况，最小二乘滤波解算爆高仿真结果如图7，图8所示。

由仿真结果可看出：滤波前后，测高误差均值差异不大，都约为0 m；滤波后测高误差标准差约为1.4 m，而单点测高的标准差约为2.1 m，可见滤波后，测高精度提高。

5 结束语

本文针对采用雷达景象匹配末制导的弹道导弹，提出了基于雷达导引头的弹道导弹爆高解算方法，由于该方法进行了信息融合处理，而无线电装置定高技术直接利用测高结果，相比之下，精度提高了2~3倍，但由于基于雷达导引头的弹道导弹爆高解算方法采用了最小二乘信息融合计算，运算量相比无线电装置定高技术较大，但弹载计算机性能在不断提高，目前计算能力已能适应最小二乘信息融合计算的要求，工程实现已成为可能。

图3 弹道、地面高程和天线波束照射区域

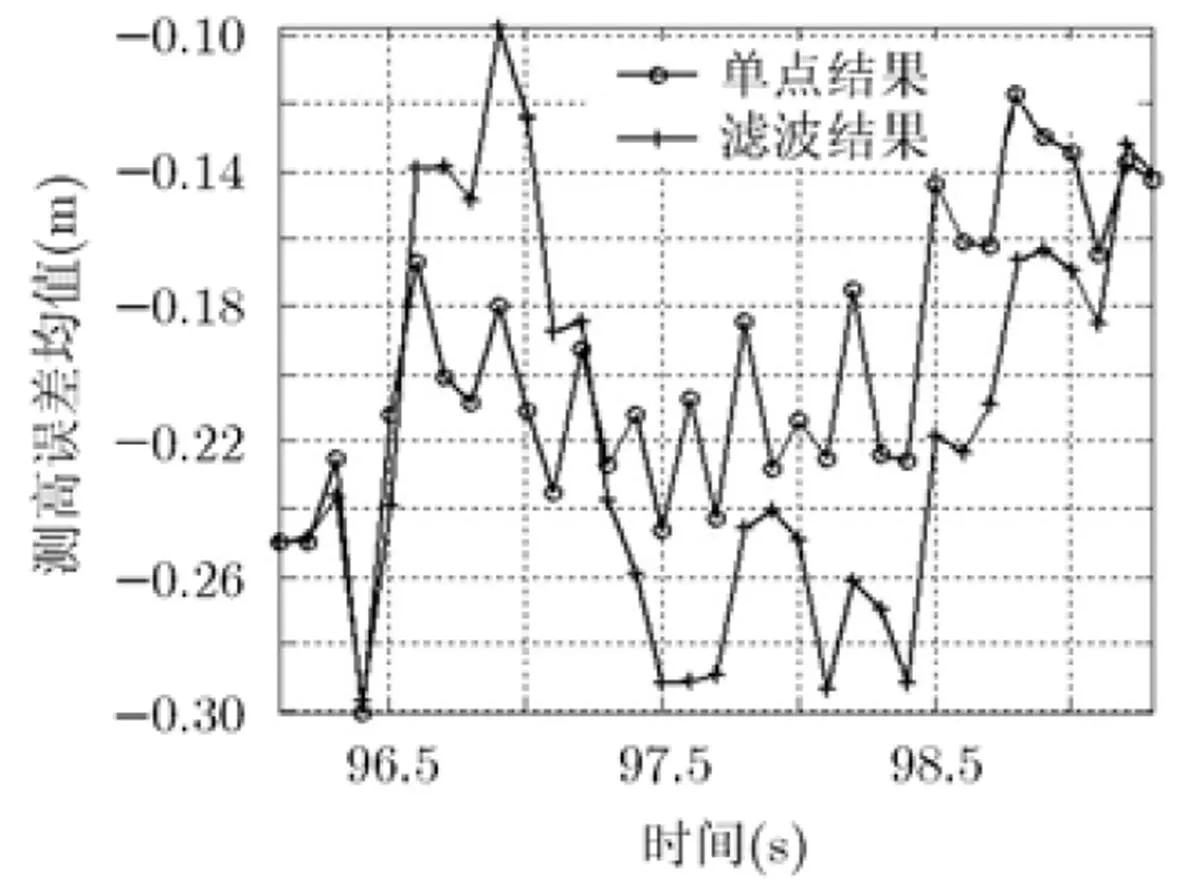
图4 测高误差均值

图5 测高误差标准差

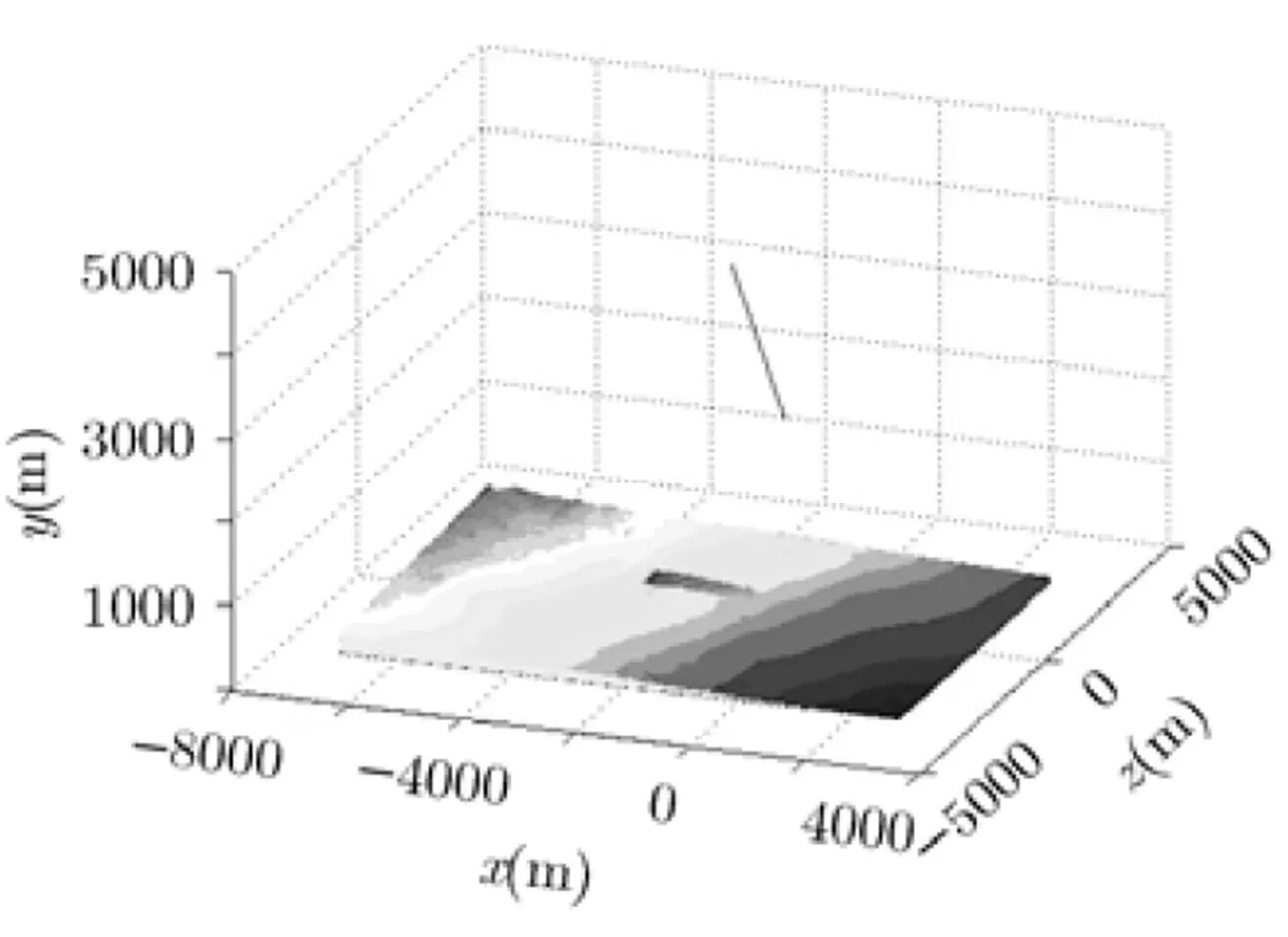
图6 弹道，地面高程和天线波束照射区域

图7 测高误差均值

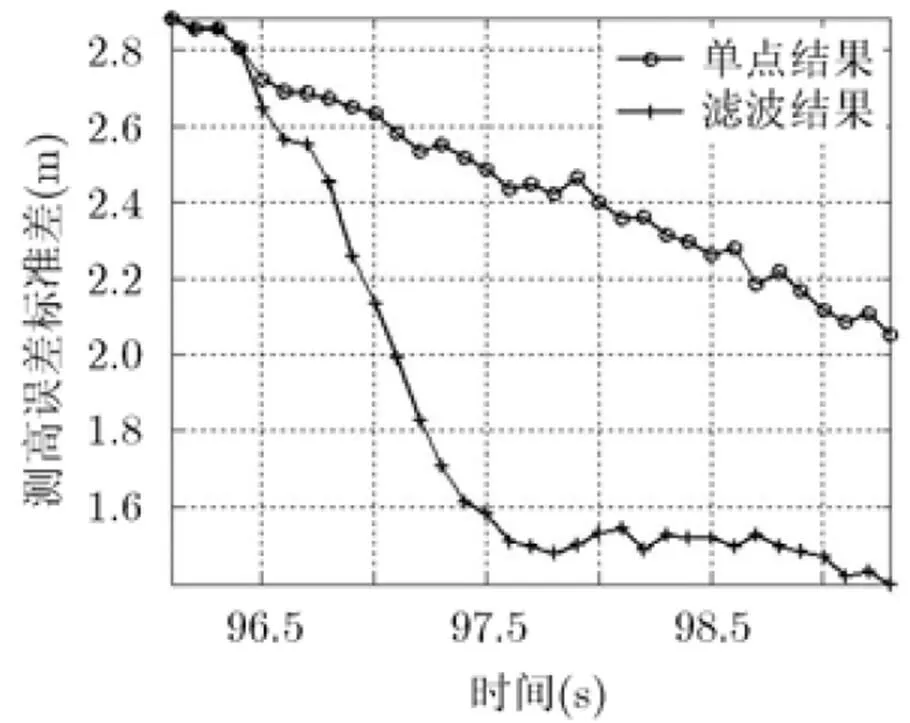
图8 测高误差标准差

[1] 王磊, 许可, 徐曦煜, 等. 一种计算雷达高度计重跟踪修正表的新方法及其应用[J]. 电子与信息学报, 2013, 35(4): 908-914.

Wang Lei, Xu Ke, Xu Xi-yu,.. A new method for computing radar altimeter look-up correction table and its application[J].&, 2013, 35(4): 908-914.

[2] 鲜勇. 基于摄动理论的爆高确定方法研究[J]. 飞行力学, 2006, 24(4): 50-52.

Xian Yong. On the method of determinating explosion height based on perturbation theory[J]., 2006, 24(4): 50-52.

[3] 廖洪昌, 郭荆燕, 何念念, 等. 一种基于BP网络的爆高延时方法[J]. 弹箭与制导学报, 2009, 29(4): 119-122.

Liao Hong-chang, Guo Jing-yan, He Nian-nian,.. A method of calculating the high-explosive delay based on back propagation[J].,,, 2009, 29(4): 119-122.

[4] 孟海东, 廖洪昌,陈奇昌, 等. 一种基于均匀设计的爆高延时计算方法[J]. 弹箭与制导学报, 2008, 28(6): 103-105.

Meng Hai-dong, Liao Hong-chang, Chen Qi-chang,.. An algorithm for burst height delay based on uniform design journal of projectiles[J].,, 2008, 28(6): 103-105.

[5] 严辉, 熊玮, 南英, 等. 战术地地导弹爆高延时方案计算与分析[J]. 导弹与航天运载技术, 1996, 24(2): 32-35.

Yan Hui, Xiong Wei, Nan Ying,.. Analysis and computation of timelag control for explosive height of tactical surface-to- surface missile[J]., 1996, 24(2): 32-35.

[6] 陈涛, 梁明. 某型无线电高度表模拟测高试验的结果分析[J]. 战术导弹技术, 2011, 31(1): 118-121.

Chen Tao and Liang Ming. Data analysis of static simulating of altitude measuring using radio altimeter[J]., 2011, 31(1): 118-121.

[7] 高善清, 魏新亮. 气压测高误差分析及修正[J]. 电子测量技术, 2012, 35(9): 60-63.

Gao Shan-qing and Wei Xin-liang. Error analysis and correction for the atmospheric pressure measurement of altitude[J]., 2012, 35(9): 60-63.

[8] 苏昂. 飞行器景象匹配测高测姿方法研究[D]. [硕士论文], 国防科技大学, 2011.

Su Ang . Study on aerial vehicles height and pose estimation method based on scene matching[D]. [Master dissertation], National University of Defense Technology, 2011.

[9] 张丽荣, 马利华, 王晓岚. CAPS气压测高的仿真分析[J]. 微计算机信息, 2011, 27(3): 185-186.

Zhang Li-rong, Ma Li-hua, and Wang Xiao-lan. Simulation analysis of CAPS barometric altimetry[J]., 2011, 27(3): 185-186.

[10] 刘玉良, 肖文杰, 崔海涛. 点头式测高雷达高度欺骗研究[J]. 舰船电子对抗, 2012, 35(4): 23-25.

Liu Yu-liang, Xiao Wen-jie, and Cui Hai-tao. Study of height deception for the nodding height-finding radar[J]., 2012, 35(4): 23-25.

[11] 刘波, 刘宝泉, 陈春晖. 机载预警雷达测高精度分析[J]. 雷达科学与技术, 2012, 10(2): 133-137.

Liu Bo, Liu Bao-quan, and Chen Chun-hui. Altitude measurement precision analysis of airborne early warning radar[J]., 2012, 10(2): 133-137.

[12] 葛仕奇, 陈亮, 丁泽刚, 等. 相位误差对InSAR相对测高精度影响[J]. 北京理工大学学报, 2012, 32(2): 179-183.

Ge Shi-qi, Chen Liang, Ding Ze-gang,.. Effects of phase error on the relative height accuracy in interferometric synthetic aperture radar[J]., 2012, 32(2): 179-183.

[13] 杜晓辉, 裴军, 张丽荣, 等. 基于地面移动通信基站的差分气压测高方法[J]. 北京航空航天大学学报, 2013, 39(1): 82-88.

Du Xiao-hui, Pei Jun, Zhang Li-rong,..Differential barometric altimetry method based on mobile phone base stations[J]., 2012, 39(1): 82-88.

[14] 刘成, 张丽荣, 杜晓辉. 一种气压测高辅助下的地面移动网定位方法[J]. 桂林理工大学学报, 2012, 32(1): 86-90.

Liu Cheng, Zhang Li-rong, and Du Xiao-hui.Terrestrial mobile network positioning method assisted by barometric altimetry technology[J]., 2012, 32(1): 86-90.

[15] 温求遒, 夏群利, 蔡春涛. 基于图像导引头及惯导相对位置信息的弹目距离估计算法[J]. 北京理工大学学报, 2012, 32(2): 141-145.

Wen Qiu-qiu, Xia Qun-li, and Cai Chun-tao. Method of range estimate based on relative position information of image seeker and INS[J]., 2012, 32(2): 141-145.

[16] 徐春夷. 国外导引头技术现状及发展趋势[J]. 制导与引信, 2012, 33(2): 11-15.

Xu Chun-yi. The present state and development trend of forein seeker technology[J].&, 2012, 33(2): 11-15.

郑宗贵： 男，1970年生，博士，高级工程师，研究方向为导航、制导与控制.

王继平： 男，1977年生，博士，讲师，研究方向为导航、制导与控制.

林红斌： 男，1964年生，博士，研究员，研究方向为导航、制导与控制.

解 静： 女，1981年生，博士，助理研究员，研究方向为导航、制导与控制.

A Calculation Method of Burst Height of Ballistic Missile Based on Radar Seeker

Zheng Zong-gui①Wang Ji-ping①②Lin Hong-bin①Xie Jing①

①(,100085,)②(96271,471000,)

At present the height of the warhead of ballistic missile is measured by the radio fuze for the burst height control of the warhead, but the reentry environment of the warhead has very high requirement for the measure set of the radio fuze, and there exists the issue of the radio fuze to be jammed. In the paper, for the ballistic missile adopting the radar scene matching terminal guidance, a calculation method of burst height of ballistic missile based on radar seeker is put forward, by fusing the height measure data of the scene matching radar seeker and the inertial navigation data, the height of the warhead is calculated in real time to realize the burst height control, which ensures the precision and improves anti-jamming capability. The validity of the method and the calculation precision of the burst height are proved by simulation and calculation.

Radar seeker; Ballistic missile; Burst height

TJ765.3+31

A

1009-5896(2014)02-0465-06

10.3724/SP.J.1146.2013.01142

王继平 wjpzj1111@163.com

2013-07-30收到，2013-11-08改回