避免颜色越界的各向异性扩散图像彩色化

陈 颖 王朔中



避免颜色越界的各向异性扩散图像彩色化

陈 颖*①②王朔中①

①(上海大学通信与信息工程学院 上海 200072)②(上海应用技术学院计算机科学与信息工程学院 上海 201418)

图像彩色化是根据人工描绘的局部初始颜色用计算机为灰度图像着色。该文提出一种各向异性的非线性扩散图像彩色化方法，该方法能够克服颜色越界问题。首先建立基于偏微分的扩散方程，通过设置自适应的张量函数，使颜色在平滑区域快速均匀扩散，在颜色交界处按各向异性方式扩散，能够有效增强边缘颜色的连贯性。算法采用有限差分法实现扩散方程的数值求解，与当前流行的彩色化技术相比，该方法能得到更加清晰自然的彩色化图像和更高的图像质量。

图像彩色化；张量；各向异性；有限差分

1 引言

图像彩色化是用计算机给灰度图像加上颜色的处理过程，是数字图像处理的一个热点问题[1]，可广泛应用于影视制作、旧照片加工、广告设计、视频编辑等领域。

常见的图像彩色化方法是一种局部颜色扩散法，该方法事先给灰度图像赋予一些初始颜色，将颜色从局部扩展到全局。Levin等人[2]用手工在图像各区域涂上适当的彩色线条，利用待着色像素与周围邻域像素的亮度关系列出彩色化方程，通过求解方程实现颜色扩散。Sapiro[3]借鉴图像修复方法引入偏微分方程(PDE)，在描绘初始彩色线条后，由亮度梯度决定的引导场将颜色扩展到整幅图像中。Kawulok等人[4]用手工涂上部分初始颜色后，用自适应竞争的方法选择颜色传播路径，再通过色度混合进行图像彩色化。随后的研究者提出了多种方法，例如基于图的半监督学习的图像彩色化[5]，应用再生核空间理论实现的灰度图像彩色化[6]，输入反映语义的检索词从互联网获得参考图像来实现的彩色化[7]，利用纹理合成技术的彩色化[8]，利用视觉线索的颜色转移方法[9]等。

现有方法往往不能很好地定位图像边缘，产生颜色越界现象，造成局部图像质量不佳。各向异性扩散是一种对图像纹理和边缘具有自适应能力的处理方法，Bertalmio曾将其用于图像修复[10]，Tripathi等人[11]研究了基于各向异性扩散的图像增强方法。为改进彩色化效果，解决边缘区域因越界扩散导致的颜色模糊问题，本文提出了一种各向异性扩散图像彩色化方法。该方法通过定义一个适当的扩散张量函数，导出用于图像彩色化的非线性各向异性扩散方程，并给出有限差分算法来求解该方程。该方法的特点是：颜色在平滑区域按各向同性方式扩散，在边缘区则按各向异性方式扩散，从而有效避免了颜色越界。实验结果表明，本文方法得到的彩色化图像色彩自然清晰，明显改善了不同颜色边界处的彩色化效果。

2 各向异性扩散图像彩色化算法

2.1 图像彩色化中的各向异性扩散

在图像平滑区，邻近像素的亮度相近，颜色值也相近，这就要求颜色梯度的2范数在平滑区域接近于零。考虑求解如式(1)的最小化问题。

泊松方程式(2)相当于各向同性扩散达到平衡时的情况，这里未考虑不同颜色交界处的复杂情况，很容易产生颜色越界。为了解决这一问题，必须对色度分量进行非均匀各向异性扩散，也就是在边缘附近沿亮度变化缓慢的方向扩散，而不越过边缘。Weickert在研究图像滤波时讨论了式(3)的各向异性扩散方程[12]：

其中是扩散方程中的加权因子。加权因子采用不同的形式会得到不同的扩散结果。当加权因子为标量常数时，是均匀各向同性扩散；加权因子是与位置有关的标量函数时是非均匀各向同性扩散；当加权因子是与位置有关的张量时，是非线性各向异性扩散，或自适应各向异性扩散。

以图像降噪为例，各向同性扩散在降噪同时平滑了图像的边缘；非均匀各向同性扩散能识别边缘，对边缘区不进行平滑；非均匀各向异性扩散可识别边缘，又能改变平滑方向，沿边缘进行平滑以取得良好的效果。

本文通过非线性各向异性扩散来解决图像彩色化问题，关键在于根据亮度分量的梯度确定合适的扩散张量，然后对色度分量进行扩散。灰度图像彩色化算法可通过求解式(4)来实现：

式中是待求图像的色度，U和U分别表示沿和方向的偏导数，div是散度算子，是扩散张量。与式(3)的不同之处在于，这里的并非直接与待求函数有关，而是由亮度分量确定的。采用合适的扩散张量函数可克服颜色越界现象，对得到效果良好的彩色化效果至关重要。

2.2 阻止颜色越界的各向异性扩散张量

文献[13]中定义了如式(5)的各向异性扩散中的结构张量：

基于结构张量导出如式(6)的各向异性扩散方程[14]：

其中()称为扩散系数。方程式(6)的性质主要取决于扩散张量，因此选择合适的是解决具体问题的关键。

将灰度图像的颜色空间从RGB空间转换到YUV空间，其中表示亮度分量，和为色度分量。对进行高斯平滑以减低噪声和中小尺度起伏的影响。计算的梯度Ñ=[YY]T，根据式(5)对每一像素(,)得到大小为2´2的结构张量：

此处高斯卷积的作用之一是平滑滤波，使结构张量具有抗噪声能力，增强鲁棒性；二是引入空间相关性，一个像素的结构张量包含其周围的信息，可体现局部结构信息。也就是说，平滑后任一像素的结构张量均受到周围像素的影响。的特征值为和，对应相互正交的特征向量为1和2。

为了防止在图像边缘处发生颜色越界，要求沿边缘的扩散强度大于垂直于边缘的扩散强度。如上所述，1指向几何结构的最大对比度方向，即指向垂直于边缘的方向，2的方向与1的方向垂直，即沿着边缘的方向。是较大的特征值，较小。为了实现沿边缘的扩散，我们令扩散系数()与特征值成反比：

将式(10)代入式(4)，得到颜色分量满足的非线性各向异性偏微分方程，同样也可得到颜色分量满足的方程。由于张量的作用，使颜色在图像平滑区按各向同性扩散，而在边缘处按照各向异性方式扩散，从而有效避免颜色越界，克服了泊松方程引起的边界颜色模糊问题。对于在平滑区域和边缘附近的作用分析如下：

(1)图像平滑区往往是相似颜色区域内部，若亮度分量完全均匀，Y和Y的值为零，则结构张量所有元素值为0，特征值==0，特征向量1=[1 0]T,2=[0 1]T，因此扩散张量为

此时不会产生各向异性加权作用，因而颜色沿所有方向均匀快速扩散。常数的取值与扩散速度有关，当大时扩散慢，会导致扩散不足，造成图像部分区域没有染上色；小能提高扩散速度，但容易出现颜色溢出的现象，造成图像部分区域颜色模糊不清；在本文实验中，取=0.01，获得了良好的实验效果。

(2)在图像边缘区域即不同颜色交界处，亮度值值有较大变化，Y和Y取非零值，因此结构张量中有非零元素出现，扩散张量产生各向异性的加权效果，颜色按各向异性方式传播，避免了图像边缘处严重的色彩混合，使边缘颜色过渡更自然。

2.3 彩色化的算法实现

本文采用有限差分法求解式(4)的偏微分方程。设扩散张量如下：

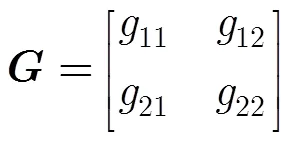
式(4)右边可展开如下：

用差分近似表示偏微商：

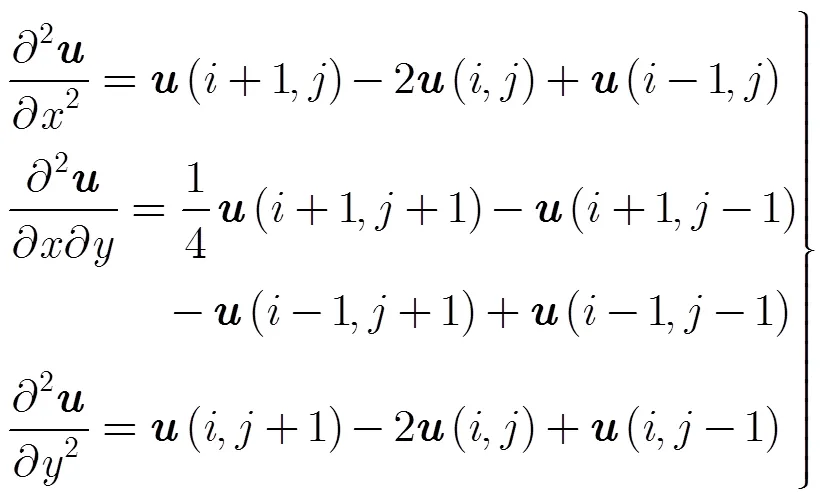
将式(13)代入式(12)，则式(4)可转化为如式(14)的迭代表达式：

(14)

基于上述讨论，实现图像彩色化的算法步骤如下：

(1)用人工方法在黑白图像的主要区域赋予初始颜色；

(2)将图像从RGB颜色空间转换到YUV空间，原黑白图像的灰度分布就是亮度分量；

(3)按式(9)计算得到扩散张量；

(5)按式(14)进行迭代计算，得到彩色化图像的分量，用同样的方法计算得到分量；

(6)将亮度和得到的色度,合并，转换到RGB空间，输出彩色化结果。

3 实验结果和讨论

实验1 采用本文算法对不同的灰度图像进行彩色化实验，得到的彩色化结果如图1所示。图1(a)列是4幅原始灰度图像，图1(b)列为初始染色情况，图1(c)列是用上述方法得到的彩色化结果。由图1可见，用本文的方法对植物、动物、人物等不同类型的图像进行彩色化，都可得到清晰自然的彩色化图像，视觉效果良好。

实验2 为验证算法稳定性，对同一幅灰度图像赋予不同的初始染色，用本文算法进行彩色化，结果如图2所示。图2(a)列是对一幅灰度图像的两种初始染色情况，图2(b)列是获得的彩色化结果。本文方法可在图像梯度较大处阻止扩散越界。图2中右下图所示实验结果中的黄色略有溢出，是由于相邻的郁金香初始颜色中含有较多黄色成分(=0,=91,=80)，在与小花交界处黄色分量梯度较小，发生了少量越界。而图2上面的例子中，初始颜色的黄色成分少(=27,=89,=19)，因而没有越界。采用文献[3]和文献[4]的方法对该图进行实验，越界现象更为明显，如图3所示，可见本文方法在边缘较弱时也有优势。

实验3 对同一幅灰度图像采用同样的初始染色，比较不同迭代次数所得结果，如图4所示。图4(a)是初始染色图像，图4(b)是迭代500次的彩色化结果，图4(c)是迭代1500次的结果，图4(d)是迭代2000次的结果。如图所示，当迭代次数较少于500次时，颜色扩散还不够充分；当迭代1500次以上时颜色扩散充分，图像彩色化结果良好。迭代500次所需要的时间约为3 s，迭代1500次所需要的时间约为5 s，迭代2000次所需要的时间约为8 s，可见在较短时间内即可获得良好的彩色化图像。

图1 本文方法彩色化实验结果

图2 本文对不同初始染色的彩色化结果

图3 文献[3]和文献[4]的方法用于图2所得的彩色化结果

图4 本文方法不同迭代次数的彩色化结果

实验4 将本文方法与文献[2]，文献[3]和文献[4]的方法进行比较，考虑视觉效果和定量指标两方面。对同一幅灰度图像，用同样的初始染色用上述方法和本文方法进行彩色化，图5所示为其中两幅图像的实验结果。3种文献的方法均有不同程度的颜色越界，本文方法效果最优。文献[2]基于相似灰度的像素点具有相似颜色的假设，在不同颜色交界处若灰度相近就会得到相似的颜色，容易产生颜色模糊。文献[3]和文献[4]分别采用基于泊松方程的各向同性扩散和自适应竞争，在边缘附近效果较差。本文方法在交界处能自适应改变扩散方向和强弱，避免颜色越界，得到自然清晰的彩色化效果。

相对于原始彩色图像，计算彩色化图像的峰值信噪比(PSNR)：

表1 4种方法的峰值信噪比(dB)

4 结束语

本文引入了自适应的扩散张量函数，建立了用于图像彩色化的非线性各向异性扩散方程。采用有限差分法求解方程，得到了计算效率高、彩色化效果优良的算法。该算法在图像平滑区域可实现快速的各向同性扩散，在边界区自适应控制扩散方向，可避免颜色越界造成的模糊。与其它同类方法相比，本文提出的方法能明显改善彩色化效果，不仅在同种颜色区域取得良好效果，而且在不同颜色交界的边缘处能保持颜色细节，得到清晰自然的彩色化图像。

图5 4种算法的彩色化结果比较

[1] Ding X W, Xu Y, and Deng L. Colorization using quaternion algebra with automatic scribble generation[J]., 2012, 7(3): 103-114.

[2] Levin A, Lischinski D, and Weiss Y. Colorization using optimization[C]. Proceedings of ACM SIGGRAPH, New York, 2004: 684-689.

[3] Sapiro G. Inpainting the colors[C]. IEEE International Conference on Image Processing, Genoa, 2005: 698-701.

[4] Kawulok M and Smolka B. Competitive image colorization [C]. IEEE International Conference on Image Processing, Hong Kong, 2010: 405-408.

[5] Liu B B and Lu Z M. Image colourisation using graph-based semi-supervised learning[J].,2009, 3(3): 115-120.

[6] Minh H Q, Sung H K, and Triet M L.Image and video colorization using vector-valued reproducing kernel hilbert space[J]., 2010, 37(1): 49-65.

[7] Chia Y S, Zhou S J, Gupta R K,Semantic colorization with internet images[C]. Proceedings of the 2011 SIGGRAPH Asia Conference, Hong Kong, 2011: 1115-1121.

[8] Wang X H, Jia J, Liao H Y,Affective image colorization[J]., 2012, 27(6): 1119-1128.

[9] Song M L, Tao D C, Chen C,Color to gray: visual cue preservation[J]., 2010, 32(9): 1537-1552.

[10] Bertalmio M, Sapiro G, and Caselles V. Image inpainting[C]. Proceedings of 27th Annual Conference on Computer Graphics and Interactive Techniques, New York, 2000: 417-424.

[11] Tripathi A K and Mukhopadhyay S. Single image fog removal using anisotropic diffusion[J]., 2012, 6(7): 966-975.

[12] Weickert J. Anisotropic diffusion in image processing[D]. [Ph. D. dissertation], University of Copenhagen, 1998.

[13] Weickert J. A scheme for coherence-enhancing diffusion filtering with optimized rotation invariance[J]., 2002, 13(1): 103-118.

[14] Tschumperlé D and Deriche R. Vector-valued image regularization with PDEs: a common framework for different applications[J]., 2005, 27(4): 506-517.

陈 颖： 女，1974年生，副教授，博士生，研究方向为图像处理、多媒体技术.

王朔中： 男，1943年生，教授，博士生导师，研究方向为图像处理、多媒体信息安全和水声学.

Image Colorization without Edge Crossover of Colors Based on Anisotropic Diffusion

Chen Ying①②Wang Shuo-zhong①

①(,,200072,)②(,,201418,)

Image colorization is to create a color picture from gray image automatically according to manually added scribbles. A colorization algorithm based on anisotropic diffusion is proposed to overcome the problem of edge crossover of colors. By defining an adaptive diffusion tensor, a nonlinear anisotropic diffusion function based on Partial Differential Equation (PDE) is established. Colors are diffused uniformly and quickly in smooth areas, while anisotropic diffusion takes place near edges, which effectively improves color transition by suppressing unwanted crossover. Numerical solution of the PDE based on a finite difference method gets satisfactory colorization effects and better quality in edge regions compared with the popular techniques.

Image colorization; Tensor; Anisotropic; Finite difference

TN911.73

A

1009-5896(2014)02-0271-06

10.3724/SP.J.1146.2013.00558

陈颖 cheny8262@163.com

2013-04-21收到，2013-10-08改回

国家自然科学基金(61071187, 61103181)资助课题