一种获取非相干分布源空间分布的算法
2014-05-29林晓帆
林晓帆 韦 岗
一种获取非相干分布源空间分布的算法
林晓帆*韦 岗
(华南理工大学电子与信息学院 广州 510640)
多数分布式信号源DOA估计算法是估计中心到达角和分布参数,不能获取真实的分布曲线,而且可能需要2维搜索,运算量大。该文在假设分布曲线形状为钟形对称的前提下,提出一种求非相干分布式信号源空间分布的算法。该算法引入稀疏信号重建作为数学工具,在阵元数充足的条件下能求解多个信号源的分布,在阵元数较少时也能得到近似求解。此外,该算法估计中心到达角的性能不逊于现存算法,且无需2维搜索,运算量低。仿真验证了以上结论。
阵列信号处理;DOA估计;非相干分布源;稀疏重建
1 引言
在阵列信号处理中,许多波达方向(DOA)估计算法都以点目标信号源为模型用以简化算法,降低分析的复杂性。然而,当信号源的空间分布特性不能忽略时,以点源为模型的DOA估计方法将不能得到可靠的估计结果[1,2]。为克服点源模型的局限,学者们提出了多种分布式信号源模型和相应的估计算法。Valaee等人[3]将分布式信号源分为相干分布源(CD源)和非相干分布源(ID源)两大类,并将标准的MUSIC方法推广为CD源和ID源两种情况下的参数估计算法(DSPE),也称“广义MUSIC”法。这一分类至今仍是一种常见的分类,后来的学者根据CD源和ID源模型发展出许多新的分布源估计算法。例如,Meng等人[4]提出分布式信号参数估计(DISPARE)算法,Lee等人[5]提出一种ID源DOA估计方法。
上述CD源和ID源模型需要假设某种确定的角信号密度函数和角功率密度函数,如高斯分布、均匀分布和三角分布等。这两个函数表示信号源的空间分布特征,在实际中不一定能预知。因此,学者们不得不尽量避免在算法中使用分布函数的具体形式信息。而分布源的估计通常也只是估计中心到达角和角度扩展。这样一来,丰富的信号源分布信息只估计出了中心到达角和角度扩展,其它分布信息丢失殆尽。
鉴于以上问题,本文尝试在不设定具体表达式,只假设分布曲线形状为钟形对称的前提下,求解ID源模型里面的角功率密度函数。这个函数代表了ID源的空间分布特征,求出它也等于知道了信号源的空间分布。

2 数据模型

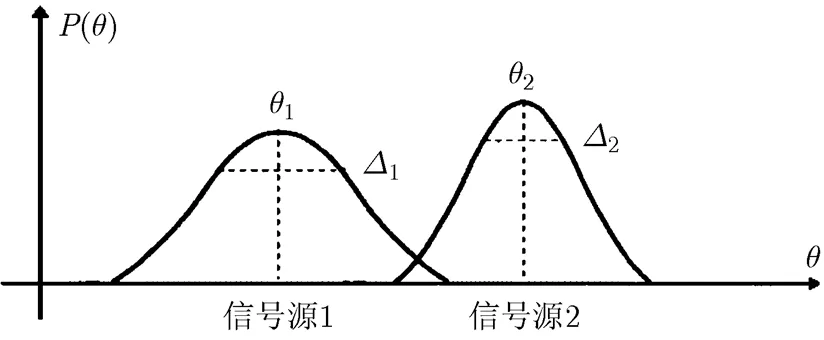
图1 两个钟形分布源在角度空间上的分布
对于非相干分布源,其不同波达方向的分量之间互不相关。假设信号与噪声无关,不同分布源之间相互独立,那么可得

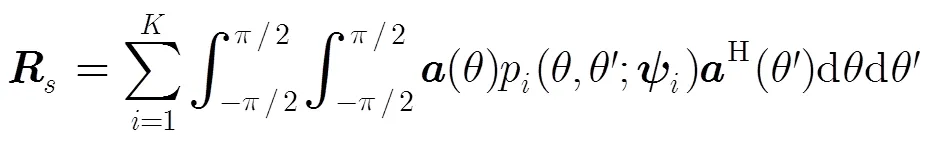
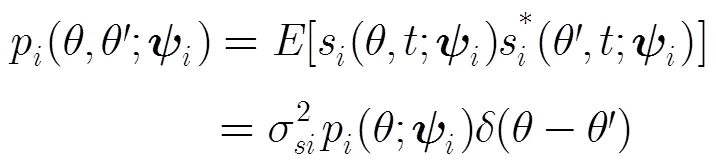
联合式(2)~式(4),可以得到非相干分布源的阵列接收数据矢量自相关矩阵。
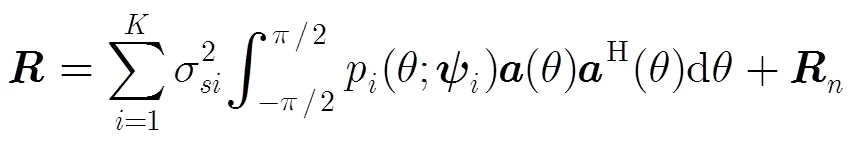

3 求非相干分布源的分布加权
对式(5)进行简化:



用求和近似表示积分,式(9)化为




一般说来,用贪婪算法解式(12)运算量小,而精度略低。具体的算法有MP, OMP及其改进算法。若将式(12)转化为式(13),用凸优化的角度求解,涉及内点法,运算量相对要高,而精度也高。具体算法有BP算法,FOCUSS等。许多关于稀疏重建或压缩感知的文献都有相关介绍,如文献[13]和文献[14]分别提出贪婪算法OMP和凸优化算法BP。
4 从分布加权中提取各分布源分布
从分布加权中提取各分布源分布的难点在于,几个信号源分布可能存在重叠,例如图1的情况。当信号重叠严重时,分离将变得困难。因此,本文假设重叠的分布至少有一边不受重叠影响或影响较小。这一假设是有其合理性的,一方面,当各信号源与阵列的距离未知时,几个分布高度重叠的信号源等效为一个分布源;另一方面,目前大多数算法不能区分分布重叠严重的信号源。
基于上述假设,从分布加权中提取各分布源分布的步骤为:
(2)以中心到达角为起点,向两边同时逐点搜索分布的边线。由于一边可能受到其它分布的重叠影响,搜索时应在左右两边选取距分布对称轴线最近的点;
(3)根据分布的对称性,将步骤(2)中选取的点复制到对称轴的另一边;
(4)插值,对步骤(3)得到的分布线求积分值,再将每一个点除以这个积分值。

5 阵元数与分布稀疏度的关系
求解式(13)需满足一定条件,先介绍如下定理。

此外,式(13)采用1范数代替式(12)的0范数,为使1范数最小化的解与0范数相同,其条件会进一步提高。目前已证明的条件有RIP条件,不相关度(mutual incoherence)条件等,可以参考文献[15-18]。然而,这些条件是充分非必要条件,对实际指导意义有局限性[17]。在实际应用中,由于不知道信号源分布的稀疏度,阵元数应越大越好。
6 算法复杂度分析和比较



7 仿真实验
本节将通过仿真实验说明本文所提算法的性能。实验中设定接收阵列为1维均匀线阵,阵元间隔为信号半波长。信号源为窄带分布源。仿真中采用1000次蒙特卡罗实验。





由图4和图5可总结出,若信号源角度扩展较大,较少的阵元也可以近似得到分布的形状,但若信号源角度扩展较小,则应使用足够的阵元数。实际应用中,若不知道信号源角度扩展,阵元数应越多越好。

图2 不同角度扩展下各算法估计的中心到达角RMSE

图3 不同信噪比下各算法估计的中心到达角RMSE

图4 角度扩展, SNR=10 dB时,随阵元数N的变化情况

图5 角度扩展, SNR=10 dB时,随阵元数N的变化情况

图6 角度扩展,阵元数N=20时,随信噪比SNR的变化情况
8 结论
本文在假设分布曲线形状为钟形对称的前提下,提出一种求非相干分布式信号源空间分布的算法。不同于传统算法,本文算法模型假设宽松(仅要求分布曲线钟形对称),能估计整个分布曲线,而不是仅估计出假设分布模型的分布参数,因此估计结果提供了更完整的分布信息,为分布式信号源的分布估计提供了一个新思路。此外,算法估计中心到达角精确度的性能不逊于现存算法,鲁棒性也相对良好。与传统算法相比,本文算法还避免了2维搜索,使得运算量通常低于传统算法。
[1] Astely D and Ottersten B. The effect of local scattering on direction of arrival estimation with MUSIC[J]., 1999, 47(12): 3220-3234.
[2] Tabrikian J and Messer H. Robust localization of scattered sources[C]. Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing, Pocono Manor, PA, 2000: 453-457.
[3] Valaee S, Champagne B, and Kabal P. Parametric localization of distributed sources[J]., 1995, 43(9): 2144-2153.
[4] Meng Y, Stoica P, and Wong K M. Estimation of the directions of arrival of spatially dispersed signals in array processing[J].-,, 1996, 143(1): 1-9.
[5] Lee J, Joung J, and Kim J D. A method for the direction- of-arrival estimation of incoherently distributed sources[J]., 2008, 57(5): 2885-2893.
[6] Malioutov D, Cetin M, and Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]., 2005, 53(8): 3010-3022.
[7] Wang Bo, Liu Juan-juan, and Sun Xiao-ying. Mixed sources localization based on sparse signal reconstruction[J]., 2012, 19(8): 487-490.
[8] Hu Nan, Ye Zhong-fu, Xu Xu,.. DOA estimation for sparse array via sparse signal reconstruction[J]., 2013, 49(2): 760-773.
[9] Xu Xu, Wei Xiao-han, and Ye Zhong-fu. DOA estimation based on sparse signal recovery utilizing weighted1-norm penalty[J]., 2012, 19(3): 155-158.
[10] He Z Q, Liu Q H, Jin L N,.. Low complexity method for DOA estimation using array covariance matrix sparse representation[J]., 2013, 49(3): 228-230.
[11] Dai J, Zhao D, and Ji X. A sparse representation method for DOA estimation with unknown mutual coupling[J]., 2012, 11: 1210-1213.
[12] Dai J, Xu X, and Zhao D. Direction-of-arrival estimation via real-valued sparse representation.[J]., 2013, 12: 376-379.
[13] Tropp J A and Gilbert A C. Signal recovery from partial information via orthogonal matching pursuit[J]., 2007, 53(12): 4655-4666.
[14] Chen S S, Donoho D L, and Saunders M A. Atomic decomposition by basis pursuit[J]., 1998, 20(1): 33-61.
[15] Candes E J and Tao T. Decoding by linear programming[J]., 2005, 51(12): 4203-4215.
[16] Candès E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509.
[17] Juditsky A and Nemirovski A. On verifiable sufficient conditions for sparse signal recovery via1minimization[J]., 2011, 127(1): 57-88.
[18] Yang Zai,Zhang Ci-shen, and Xie Li-hua. Robustly stable signal recovery in compressed sensing with structured matrix perturbation[J]., 2012, 60(9): 4658-4671.
[19] Ghogho M, Besson O, and Swami A. Estimation of directions of arrival of multiple scattered sources[J]., 2001, 49(11): 2467-2480.
[20] Shahbazpanahi S, Valaee S, and Bastani M H. Distributed source localization using ESPRIT algorithm[J]., 2001, 49(10): 2169-2178.
林晓帆: 男,1990年生,博士生,研究方向为阵列信号处理、通信信号处理.
韦 岗: 男,1963年生,博士生导师,教授,研究方向为信号处理、无线通信.
A Method to Obtain the Spatial Distribution of Incoherently Distributed Sources
Lin Xiao-fan Wei Gang
(,,510640,)
Most DOA estimation algorithms of distributed sources only estimate central angle of the arriving signal and its distribution parameters. These methods can not obtain the real distribution curve, and may require a two-dimensional search which costs a large amount of computation. In this paper, a method to obtain distribution curves is proposed on the assumption that the distribution curves are bell-shaped and symmetrical. Furthermore, the sparse signal reconstruction is introduced as mathematical tools, and it works well in the condition of sufficient number of array elements and can still obtain an approximate solution with insufficient array elements. In addition, its performance to estimate the central angle of arriving signal is not worse than the existing algorithm. Without requirement for a two-dimensional search, this method has lower computational complexity. Simulations verify the above conclusions.
Array signal processing; DOA estimation; Incoherently distributed sources; Sparse reconstruction
TN911.7
A
1009-5896(2014)02-0260-06
10.3724/SP.J.1146.2013.00601
林晓帆 walkerlin@foxmail.com
2013-05-03收到,2013-08-12改回
国家973计划项目(2011CB707003), 高等学校博士学科点专项科研基金(20130172120045)和中央高校基本科研业务费专项资金项目(2014ZZ0034, 2014ZB0030)资助课题
