基于ANSYS和MATLAB智能算法的电石热物性参数反演

2014-05-28王彦龙屈福政

冶金设备 2014年2期

王彦龙屈福政

(大连理工大学机械工程学院辽宁大连116024)

1 引言

电石是一种重要的化工基础原料，广泛应用于生产乙炔、有机合成、氧炔焊接和钢铁脱硫等领域，在国民经济发展中具有不可替代的作用。目前工业上主要采用电炉还原法生产电石，由氧化钙和焦炭在2200℃的高温下反应制得，化学反应方程式为Ca0+3C=CaC2+CO［1］。电石从出炉口进入电石锅后逐渐冷却、凝结，其冷凝和降温过程决定着电石锅的形状、布置和倾翻作业的节拍，因此研究电石在冷却过程中的温度场分布具有十分重要的意义。

但是，由于电石的出炉温度高达2000℃，现场不能立即进行测量，且实验只能测到表面若干点处的温度值，无法直接测量获得电石内部温度分布。因此只能通过软件仿真的方法获得电石冷却过程中的温度场分布。而仿真需要电石的热物性参数，但是由于国内目前在材料热物性参数方面的数据和研究较少，缺少电石从常温到2000℃这么宽范围内的导热系数值。

为此，本文提出一种新的研究思路，依据现场测得的有限的表面温度数据，通过参数反演获得电石的导热系数，希望能对电石出炉系统设计和生产流程控制起到指导作用，并为获得物质的热物性参数提供一种新的研究思路。

2 技术路线

由于求解物质的热物性参数是一种反问题，从数学的角度来讲，反问题是一种病态问题，由于其对误差极其敏感，传统的算法不仅计算量巨大，而且很难收敛得到精确解。神经网络是一种模仿生物神经网络的结构和功能的计算模型，具有分布、并行、自学习等特点;遗传算法是一种借鉴生物界自然选择和进化机制发展起来的搜索优化算法，具有高度并行、自适应、全局收敛等特点。神经网络与遗传算法结合，特别适合解决这种复杂的非线性问题［2］［3］［4］。

探讨利用ANSYS热分析模块、神经网络和遗传算法进行参数反演得到电石的一个热物性参数——导热系数随温度变化的值。分析中ANSYS用于对电石冷却过程进行仿真，得到的数据作为神经网络的训练样本和测试样本;神经网络在MATLAB中代替ANSYS作为传热问题的求解器，用于参数反演中的数据生成;遗传算法进行参数反演得到电石导热系数随温度变化的值。

具体的技术路线为:利用遗传算法中的随机函数，生成一系列的可行解;将它们输入到ANSYS中，仿真得到电石冷却过程的温度分布样本;利用这些样本训练和测试神经网络，得到的神经网络进行参数反演过程中的数据生成;利用遗传算法进行参数反演，最终得到的最优解即为所求的不同温度下电石的导热系数值。其流程如图1所示。

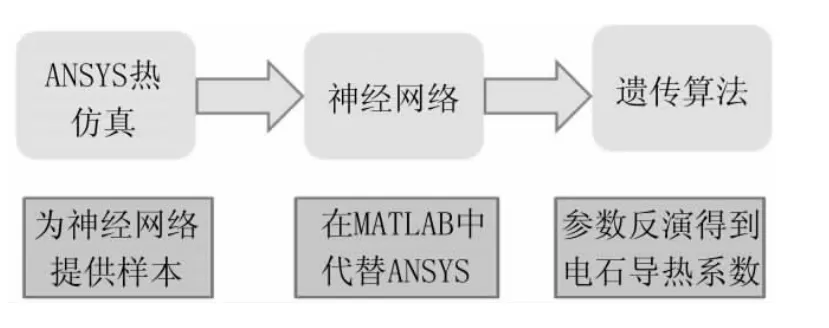
图1 技术路线

3 ANSYS热仿真

3.1 建立模型

电石的冷却过程是一个瞬态过程，在ANSYS的热模块中进行仿真。建立电石二维传热模型(轴对称)如图2 所示［5］。

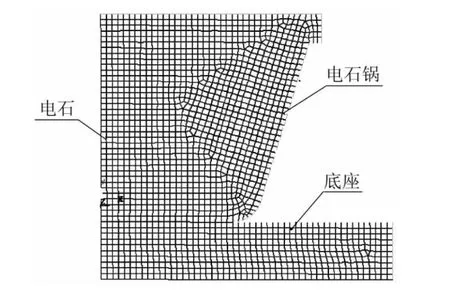
图2 电石传热模型

传热模型由电石锅、电石和底座三部分组成，模拟出炉后的两个小时中电石在电石锅中的冷却过程。采用的单位制为千克(kg)、毫米(mm)、秒(s)、摄氏度(℃)，仿真中的参数单位均需换算到该单位制。电石锅的材料为铸钢，底座的材料为结构钢，涉及到的热物性参数有密度、比热、导热系数［6］［7］。其中，电石的导热系数为待求量，由于其值随温度变化，在综合考虑精确性与计算量之后，决定将其温度划分为5个区间，设计其格式如表1所示。

表1 电石导热系数格式

分析中用到的ANSYS热分析单元有PLANE55单元和SURF151单元。其简介及关键选项设置如下。

PLANE 55为2维4节点热实体单元，可作为平面单元或轴对称环单元，用于2维热传导分析，每个节点只有一个温度自由度，适用于稳态热分析和瞬态热分析。本单元必须位于总体坐标的X－Y平面中，对于轴对称问题，Y轴必须是对称轴，结构模型必须在+X部分。此次仿真中的电石、电石锅及底座均用PLANE 55单元建模，需在单元选项中打开轴对称(Axisymmetric)。

SURF151为表面效应单元，在这个传热模型中，由于需要在电石锅外表面上同时施加辐射和对流边界条件，因此需要用到表面效应单元，将其中一个施加在实体单元表面，而另一个施加在表面效应单元上。为灵活施加边界条件，需要单独新建一个材料类别，定义的材料属性有辐射率(在材料属性中定义，EMIS)和玻尔兹曼常数(在实常数中定义，Stefan-Boltzmann const，5.67 ×10－8W/(m2·K4))。

表面效应单元类似一层皮肤，覆盖在实体单元的表面。它利用实体表面的节点形成单元，因此不增加节点数量而只增加单元数量。ANSYS中2维热分析用到的表面效应单元为SURF151，此次热分析在表面效应单元上施加辐射边界条件。

电石冷却过程中热量通过热对流及热辐射方式散失到空气中，因此这是一个开放的系统。ANSYS中热分析的基本原理是能量守恒，因此需要定义一个外部节点，用于吸收损失的辐射热量。这个节点的位置是没有具体限制的，在模型外部即可。

SURF151单元中关键的分析选项设置如下:

KEYOPT(3)=1 Element behavior-Axisymmetric轴对称;

KEYOPT(4)=1 Midside nodes-Exclude无中间节点;

KEYOPT(5)=1 Extra node for radiation-Include 1 node有外部节点;

KEYOPT(9)=1 Radiation form fact cacl as－Real const FORMF考虑辐射，角系数法。

3.2 施加载荷及求解

分析类型选择瞬态分析(Transient-Full)，在求解控制选项卡中设置求解选项。仿真中只有一个载荷步，在时间控制中设置仿真时间、打开自动时间步、设置子步步长;因为后处理中需要整个热仿真过程中的数据，因此需要设置保存所有子步的结果;其他的选项按照程序默认设置即可。由于热辐射的存在，需要设置温度偏移量，将温度转换为绝对温度，偏移量为273。

初始条件为:电石初始温度2000℃，而电石锅和底座初始温度25℃。

边界条件为:对流和热辐射的边界均为电石的上表面、电石锅的外表面和底座的外表面，在表面效应单元上定义热辐射边界条件，在实体单元上定义对流边界条件;底座底面为绝热条件。

在每次仿真中，将程序随机生成的可行解输入到传热模型中，设置初始条件，然后求解并保存结果。

3.3 后处理

在后处理模块中对仿真结果进行分析。

在通用后处理器中选择Read Results-By Time/Freq，设置时间，读取此时的计算结果，即可查看该时刻电石的温度分布云图。

在时间－历程后处理器中可以查看结果随时间变化情况。选取电石表面中心点处节点，查看其节点温度随时间变化情况，以数据列表形式(.lis)保存结果。将数据文件导入EXCEL中，即可对数据进行操作，得到每10分钟选定点处的温度值(共13个)。以后每次求解、保存数据文件之后，只要在EXCEL中进行刷新操作，即可得到选定点处每10分钟的温度值，大大提高了数据处理效率。

4 神经网络

神经网络，又称人工神经网络，是一种模仿生物神经网络的结构和功能来进行分布并行处理的数学模型，由大量的人工神经元联接而成，可根据外界信息调整内部节点间的相互联接关系，从而达到处理信息的目的。由于其分布、并行、自学习等优越特性，在人工智能、自动控制、计算机科学、信息处理、机器人、模式识别等方面有着重要的应用［8］。

BP神经网络是目前应用最广泛的神经网络模型，采用误差反向传播算法，误差逐层回传，以修正层与层之间的权值和阈值。由于单隐层BP网络有较强的非线性映射能力，因此选用了单隐层BP神经网络。

神经网络算法是在MATLAB神经网络工具箱中编写完成的。因为在ANSYS中每次输入的导热系数值有5个，而输出的温度值有13个，因此输入层神经元个数为5，输出层神经元个数为13，隐含层节点数的经验公式为:

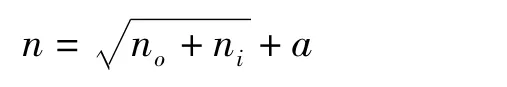
式中 ni—输入层神经元个数;

no—输出层神经元个数;

a—1～10之间的一个自然数。经过测试，当时，神经网络的性能最好，，因此选取隐含层节点数为15。利用ANSYS仿真得到的数据训练神经网络，经测试其性能达到要求后，保存该神经网络。得到的网络在遗传算法中作为传热正问题的求解器，进行数据生成。

神经网络结构如图3所示。

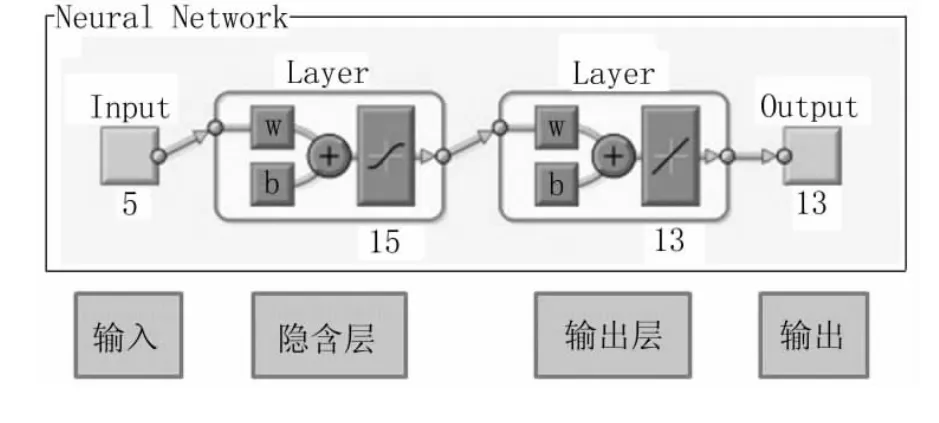
图3 神经网络结构

5 遗传算法

遗传算法是一种借鉴了达尔文进化论和孟德尔遗传学说，模仿自然界生物进化规律发展起来的随机全局搜索、优化方法，是计算机科学人工智能领域中用于解决最优化问题的一种搜索启发式算法，属于进化算法的一种。它提供了一种求解复杂系统优化问题的通用框架，不依赖于问题的具体领域，使用简单、鲁棒性强、易于并行化，广泛应用于各个学科中。目前，遗传算法在参数反演、模式识别、人工智能、机器人学、自动控制、图像处理、人工生命等诸多领域都得有较多应用，是一种求解全局优化问题的有力工具［9］。

遗传算法的实现主要涉及5个方面的内容，下面将从这5个方面对此次参数反演中的遗传算法的原理方法、参数设置等进行介绍。

5.1 参数的编码

参数编码是遗传算法需要首先解决的问题，是遗传算法的一个关键步骤。编码的好坏直接影响着选择、交叉、变异等之后的一系列遗传操作。

遗传算法的编码方法较多，大致可以分为三类:二进制编码、符号编码、浮点数编码。在二进制编码中，参数均被表示为由{0、1}组成的二进制串，由于其编码、解码过程简单易行，交叉、变异操作便于实现，是目前使用最为广泛的编码方法，因此此次参数反演中选用了二进制编码方法。

由于要求解的电石的导热系数值随温度变化，在综合考虑计算精度及计算量之后划分为5个区间，共有5个值，其形式见表1。在编码操作中，这5个值被转换为二进制串，呈线性排列在一起，组成问题的一个可行解。各二进制串长度均取为20，且在迭代过程中长度保持不变。

5.2 初始种群设定

在遗传算法流程中，参数编码后的任务是对初始种群进行设定。需要根据实际问题，确定种群的规模、最优解的分布范围，然后在此分布范围内设定初始种群。遗传算法程序根据所给定条件，随机产生初始的个体，这些个体构成初始的种群，并以此为起点一代代的进化，直至得到最优解，终止进化过程。

5.3 适应度函数设计

在遗传算法中，适应度是评价个体性能的唯一依据。由于适应度的大小直接决定了个体遗传到下一代的概率，影响着遗传算法搜索优化的方向和最终结果的获得，因此适应度函数的设计在遗传算法设计中有着重要的意义。

适应度函数也称评价函数，是根据目标函数确定的用于区分种群中个体优劣程度的标准。在遗传算法中，规定适应度函数是非负的，且值越大越好。而实际问题中目标函数种类繁多，函数值有正有负，优化目标可能是求最大值也可能是求最小值，因此需要利用适应度函数将目标函数值转换为相对适应度值。

此次参数反演的目的是要根据实测的电石表面温度得到电石随温度变化的导热系数值，在编写的遗传算法程序中，目标函数是仿真值与实测值的残差，优化目标是求目标函数的最小值。本文中使用的是基于线性排序的适应度计算方法，首先对目标函数进行降序排列，每个个体的适应度值根据其在排序种群中的位置计算出来。

5.4 遗传操作

遗传操作主要包括选择、交叉、变异，它们在遗传算法中起着核心作用，需要根据实际问题选择合适的操作算子。

选择操作是建立在对个体的适应度进行评价的基础之上的，个体被遗传到下一代的概率与其适应度值大小成正比，适应度大的个体被遗传到下一代的概率就大，而适应度小的个体被遗传到下一代的概率则小。选择操作有效地避免了有用遗传信息的丢失，提高了全局收敛性和计算效率。

此次参数反演中使用的随机遍历抽样方法是一种经典的选择方法，个体被选择的概率与其适应度成正比，每次随机选出一对个体，让这两个个体进行竞争，适应度高的个体被选中，如此反复直至选满。这种方法有效地避免了比例选择方法中选择误差大的问题，是一种较好的选择方法。

交叉操作是遗传算法中产生新个体的主要方法，决定着遗传算法的收敛性和全局搜索能力，起着关键的作用。交叉算子的设计和实现与实际问题密切相关，需要和编码设计一起考虑，主要包括如何确定交叉点位置和如何进行部分基因交换两个方面的内容。

交叉操作的过程是:用随机的方法对种群中的个体进行配对，将种群中的M个个体组成M/2对配对个体组;按预设交叉概率决定每对个体组是否需要进行交叉操作;设定配对个体组的交叉点;进行交叉操作。此次选用的交叉方法是使用最多的单点交叉方法，是在个体组串结构中随机设定一个交叉点，对该点处部分基因进行交换。

变异操作是遗传算法中产生新个体的辅助方法，决定着遗传算法的局部搜索能力，是必不可少的一个重要步骤。变异操作的一般步骤是:在种群所有个体的码串范围内随机确定基因座;以预设的变异概率改变此处的基因值。通常变异概率值非常小，对于二进制编码来说，变异操作就是把某些基因座上的基因值由1变为0，或是由0变为1。此次选用的是离散变异。

5.5 遗传算法的控制参数设定

遗传算法中的控制参数主要包括种群规模、交叉概率、变异概率等。它们对算法的性能和收敛性有着较大的影响，因此这些参数的选取非常关键。下面将详细讲解这些参数的选取过程。

5.5.1 种群规模

种群规模直接影响着遗传算法的收敛性和计算效率，应合理选取。种群规模越大，则群体中个体的多样性越高，算法陷入局部最优解的可能性越小。但是种群规模过大会产生两种弊端:一是大大增加算法的计算量，影响算法计算效率;二是导致少量适应度值很高的个体被选择生存下来，大多数个体被淘汰，影响交叉操作。一般种群规模的取值在10～200之间，经过多次尝试后，选择了种群规模为50。

5.5.2 交叉概率

交叉概率控制着遗传算法中交叉操作被使用的频度，其取值需要合理选取，否则可能会造成一些意想不到的后果。较大的交叉概率可使各代充分交叉，有利于保持种群的多样性;但若过大则会使群体中的优良模式遭到破坏，产生较大的代沟，导致搜索走向随机化。交叉概率越小，产生的代沟的就越小，种群中的优良模式能顺利遗传到下一代，得到全局最优解的可能性就越大;但若过小，则会使种群进化的速度过慢甚至陷入停滞状态，无法得到全局最优解。通常交叉概率的取值范围在0.4 ～0.99 之间，根据实际问题，取为0.7。

5.5.3 变异概率

变异操作是交叉操作有效补充，决定着算法的局部搜索能力，变异概率的值也需合理选取。较大的变异概率能产生较多的新个体，从而增大种群的多样性，但可能破坏种群中较好的模式，使搜索走向随机化;但若过小，则算法容易陷入局部最优解中。通常变异概率的取值范围在0.0001～0.1 之间，根据实际情况，取为0.01。