电机系统载荷惯量在线测试方法与试验研究

王子辉，王文明

（1．浙江科技学院 自动化与电气工程学院，杭州310023；2．浙江工业大学 之江学院，杭州310024）

电机驱动的调速系统在工业和民用应用中使用广泛，如在电梯、抽油机中作为提升机构，在车船等交通工具中作为推进机构，在风机、泵类、压缩机中作为旋转机构，以及在数控机床、机器人和计算机外围设备等高精度伺服领域作为定位机构等。转动惯量可以表征系统受力矩作用而引起转速变化的程度，大惯量系统的转速保持力较好，抗外界扰动能力就强；小惯量系统的速度变化容易，调速性能就好，因此转动惯量影响系统的动态性能。针对不同的用途、不同的电机驱动系统需要达到相应的动态性能，这就要首先测试系统载荷状态下的转动惯量，使得设计的电源功率或者驱动器容量能够与系统要求的动态性能相匹配。

获取转动惯量的方法有许多种，传统的测试方法根据机械惯量的基本属性，有扭摆法、悬吊法和落重法等［1－3］。这些方法可以测量电机空载时的转动惯量，但不能测量电机带负载后系统整体的转动惯量，这就限制了它的实际应用价值，而且测量过程对仪器、工装等都有较高要求。因此，实用的惯量测试方法一般按照惯量的“力矩－速度”效果特性，有谐振运动法、在线参数辨识法和自由减速 法［4－13］等 。

文献［4］提及谐振运动法，向伺服电机施加谐振电磁力矩而使转子产生谐振运动，根据瞬态振荡过程求解得到系统的转动惯量。在线辨识法主要使用各种参数自适应算法求解转动惯量：文献［5］结合了最小二乘法并引入遗忘因子，对转动惯量在线参数辨识过程做了仿真研究；文献［6－9］采用卡尔曼滤波器、模型参考自适应和龙贝格观测器等自适应算法，这类方法的特点是响应十分迅速，它通常可以在电机驱动系统运行的几毫秒内求解得到系统惯量，但是计算过程和参数设置较复杂，对控制系统的性能要求很高。

自由减速法能够测试系统带负载时的整体惯量，测试方便，计算简单。将电机系统带到一定转速，然后切断供电电源，旋转机构依靠惯性自由减速，减速过程中测试系统参数并根据惯性方程求解转动惯量［10－11］。文献［12－13］采用了改变系统惯量的自由减速法，分别测试了施加和不施加已知惯量飞轮的自由减速过程，计算得到系统的转动惯量。但测试过程中需要安装和拆卸已知惯量的飞轮，这在大部分应用现场操作不便，仅适用于实验室测试阶段。

本研究探讨了电机驱动系统在各种常见负载工况下的自由减速过程，建立了自由减速过程的数学模型，并求解出系统转动惯量的精确解析解，最后通过软件仿真和实际带负载测试，验证了该方法的准确性。与其他惯量测试方法相比，这种改进的自由减速法实施起来更为可靠，通用性好，在现场调试过程中实用性较强。

1 负载类型及惯量特性研究

系统的转动惯量受各种因素影响，如电机自身的转子惯量、负载的类型等。对于同一根转动轴而言，物体不同部分的转动惯量可以用代数叠加，所以可以将系统的整体惯量等效为一个总值，基本方程描述为［14］：

式（1）中：ωr—电机转子的转速；J—综合考虑各种因素之后的总体系统惯量；Te—电机电磁转矩；TL—总负载力矩，它包括了负载力矩、黏滞摩擦阻力矩和其他扰动等。

摩擦阻力矩与其他扰动转矩一般与转速成一次和零次的关系，可以统一描述为TLf＝Bmω＋C，但只占了总负载的很小一部分，因而总负载力矩通常只考虑载荷的负载力矩。

常见的负载类型主要有以下几种：

1）恒功率负载。恒功率负载的转矩与转速成反比关系，功率保持恒定。电钻和轧钢机等机械的负载特性属于恒功率负载。这类负载的特点是低速重载，高速轻载。

2）恒转矩负载。恒转矩负载的转矩是常数，不随转速变化而变化，负载的功率变化与转速变化成线性关系，例如电梯和升降机等，大约90%的工业机械负载属于恒转矩负载。

3）一次型负载。转矩与转速成正比关系，功率与转速成平方关系，例如直流电机负载和搅拌机等。

4）二次型负载。转矩与转速成平方关系，功率与转速成三次关系。绝大多数泵类和风机属于二次型负载。

5）不规则负载。转矩变化取决于其他因素，如压缩机负载与转子位置、转子转速和吸排气口压力差都有关系，属于不规则负载［15］。

如果确定了系统的负载类型，即可拟合负载转矩与转速的关系式（2），如表1所示。

表1 负载转矩与转速拟合关系Table 1 Load torque vs．speed

2 解析法求解系统惯量

2．1 自由减速过程的解析表达

根据电机的电磁 －机械关系式（1），如果系统在带负载稳定运行时切断供电电源，电磁转矩Te为零，电机将在负载转矩的作用下作自由减速运动，直到停止旋转。其过程可表示为：

如图1所示，自由减速过程的初始转速为ω0，在t1时刻切断电源，转子开始减速，至t2时刻完全静止，这一过程所经历的时间定义为自由减速时间Δt。转子转速逐渐降低，而负载转矩也按照负载特性随转速改变，因此，以转速为研究对象描述该物理过程：

图1 自由减速过程Fig．1 Free retardation process

令Δt＝t2－t1，联立式（2）和式（4）并代入初始和终止条件，使用专业数学求解工具Maple，解得各负载类型自由减速过程的转速随时间的关系及转动惯量：

恒功率负载：

恒转矩负载：

一次型负载：

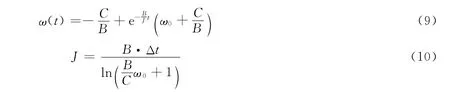
二次型负载：

式（11）中：Δ＝4AC－B2。

考虑最终时刻的停转状态，令ω（Δt）＝0，得：

以上给出了各种负载类型的系统转动惯量的解析表达式，如果与负载特性相关的量P、A、B和C已知，结合初始速度ω0和自由减速时间Δt，即可求出转动惯量。

2．2 负载特性拟合系数

不同类型负载的参数可以根据负载表达式（2）求解。电机驱动系统带负载稳定运行时，驱动转矩等于负载转矩。通过转矩测试仪的读数或者电机电磁关系计算可以得倒驱动转矩，也就知道了系统的负载转矩。在同步dq坐标下，各种交流电机的转矩可统一表示为［16］：

式（13）中：ψ—气隙磁链；i—定子电流；d、q—表示dq坐标系下的分量。

以永磁电机为例，当采用常规的id＝0控制方式时，转矩表达式为：

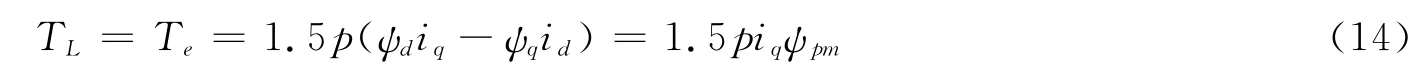
由此可以根据定子电流测算出系统稳定运行时的负载转矩。

以二次型负载模型为例，测定系统在3次不同转速下稳定运行时的负载转矩，从方程组（15）中求解得到系数A、B、C：

同理，一次型系统测试2次负载转矩，恒转矩系统和恒功率系统测试1次负载转矩，就可以求解得到负载系数。需要指出的是，不规则负载如压缩机系统的等效转轴不止1根，因此，它的系统惯量不是常数，就不能用解析式表示等效的惯量。

3 仿真与试验

为了验证解析算法，试验中分别搭建了仿真平台和实物测试平台。使用Matlab／Simulink对恒转矩系统、一次型负载系统和二次型负载系统的自由减速过程进行仿真，系统包含了矢量控制算法、电机数学物理模型、负载模型和转动惯量计算单元，图2所示为永磁同步电机驱动的负载模型框图。试验平台测试了永磁电机驱动的直流电机负载系统和风机负载系统的自由减速过程，如图3所示。

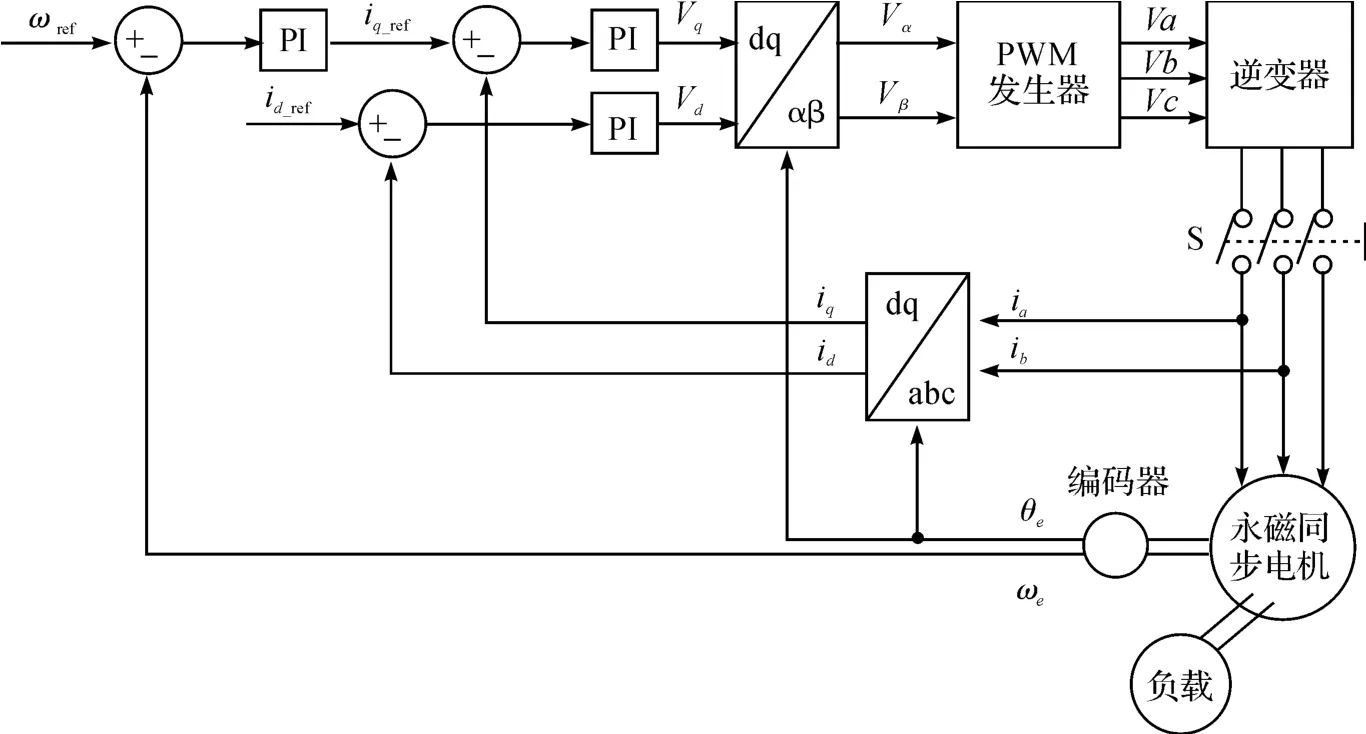
图2 永磁电机矢量控制系统Fig．2 Vector control system of PMSM

图3 永磁电机自由减速试验平台Fig．3 PMSM free retardation platform

系统由驱动控制器、永磁电机、负载机构和测量仪器组成，测量仪器包括电流传感器、速度／位置编码器和计时程序，分别用来测量转矩电流、转速和自由减速时间等。电机和负载的有关参数见表2。

表2 系统参数Table 2 System parameters

3．1 仿真测试一次型负载系统惯量

永磁电机与直流电机的轴联系统中，永磁电机作为驱动机构，直流电机作为负载。在永磁电机的仿真模型中预先设定转动惯量为J＝0．002 4kg·m2。负载转矩的一部分来自直流电机电刷的阻力矩，为恒定负载，另一部分是轴承摩擦产生的与转速成一次方关系的黏滞阻力矩，因此，负载模型为一次型负载，如式（2－c），指定负载系数B＝0．000 28，C＝0．180。在均速3 000r／min时打开开关S，切断电源后电机依靠自身惯性和负载的作用减速至零，仿真结果如图4、图5所示。

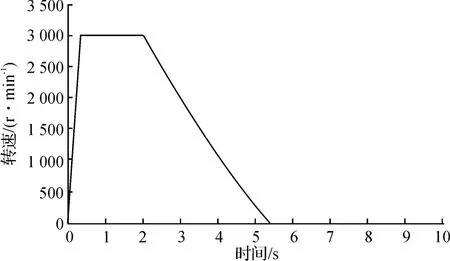
图4 一阶直流机负载自由减速过程的转速变化Fig．4 Speed variation of free retardation process with 1st－order DC motor load

图5 一阶直流机负载自由减速过程的转矩变化Fig．5 Torque variation of free retardation process with 1st－order DC motor load

从图4和图5中测试得到自由减速过程经历的时间为Δt＝3．41s，将初始转速、减速时间和负载系数代入到惯量计算式（10）中计算得：J＝0．002 4kg·m2，与给定值吻合。如图6中惯量求解器所示，由此验证了解析解的正确性。

3．2 测试二次型负载系统惯量的试验验证

风机类负载的阻力矩一般与转速成二次方关系，实验测得不同转速稳定运行时的转矩电流和自由减速时间，如表3所示。

图6 Simulink中的惯量求解器Fig．6 Inertia calculator in Simulink

由式（14）和表3解得 A＝1．09×10－5，B＝5．82×10－4，C＝9．6×10－3，再根据式（12）解得转动惯量J＝2．0×10－3kg·m2。将计算得到的系统参数代入到Simulink模型中进行仿真，得到一条速度随时间变化的自由减速曲线（图7）和负载转矩随时间变化的曲线（图8）。实测试验中，在风机以匀速1 200r／min运行时断开开关，记录10s自由减速过程，编码器把速度值反馈给控制器，并从存储单元中提取数组，绘制出实测的自由减速转速曲线（图7）。对比仿真与实测的转速曲线，可以较直观地看出2条曲线比较接近，它们从相同时刻开始减速，在相同时刻停止，这说明采用解析算法得到的负载表达式和转动惯量能够准确描述实际系统的运动过程，也能准确解得系统惯量。

表3 风机负载系统自由减速实验结果Table 3 Free retardation experiment results of wind－turbine system

图7 二阶风机负载系统自由减速过程的转速变化对比Fig．7 Speed comparison of free retardation process with 2nd－order fan－type load

图8 二阶风机负载系统自由减速过程的转矩变化Fig．8 Torque variation of free retardation process with 2nd－order fan－type load

4 结 语

本研究通过拟合和解析推导得出了电机系统载荷转动惯量的解析解，并给出了实际应用中测试系统转动惯量的方法。采用该方法可以实现系统转动惯量的在线测量，而且测量精确度高，适用范围广。在不同转速和负载的测试条件下对比了仿真和实测结果，其吻合程度较高，从而证明了该方法的实用性。

［1］ 吴晓慧．旋转电机转子转动惯量测定方法［J］．中小型电机，2005，32（2）：62－65．

［2］ 徐丽，张文海．分装式电机转子转动惯量的简易测量［J］．微特电机，2006，34（8）：44－45．

［3］ 刘博伟．电机转子转动惯量获取方法研究［J］．微电机伺服技术，2006，39（3）：97－100．

［4］ Andoh F．Inertia identification method based on the product of the integral of torque reference input and motor speed［C］∥IEEE International Conference on Control Applications．San Antonio，Texas：IEEE，2008：1151－1158．

［5］ 刘永钦，沈艳霞，纪志成．基于改进型最小二乘法的感应电机转动惯量辨识［J］．电机与控制应用，2008，35（12）：13－17．

［6］ Cao X Q，Bi M．Extended luenberger observer based on dynamic neural network for inertia identification in PMSM servo system［C］∥International Conference on Natural Computation．Tianjin，China：IEEE，2009：48－52．

［7］ 夏加宽，盛丽君．转台系统转动惯量辨识与控制器参数自调整［J］．沈阳工业大学学报，2008，30（6）：605－608．

［8］ 卢少武，唐小琦，宋宝，伺服系统转动惯量辨识及其应用［J］．微电机，2011，44（10）：41－43，88．

［9］ Hong S J，Kim H W，Sul S K．A novel inertia identification method for speed control of electric machine［C］∥Industrial Electronics，Control，and Instrumentation．Taipei：IEEE，1996：1234－1239．

［10］ 刘旭，阮毅，张朝艺．一种异步电机转动惯量辨识方法［J］．电机与控制应用，2009，36（9）：1－3．

［11］ 于伟，马佳光，李锦英，等．基于LuGre模型实现精密伺服转台摩擦参数辨识及补偿［J］．光学精密工程，2011，19（11）：2736－2743．

［12］ 周海方，王雪帆．电机转子转动惯量的测量［J］．电气技术，2006（12）：37－40，48．

［13］ 林孙奔，沈宇雯，王波，等．基于电机自由减速过程的转子转动惯量测量方法［J］，微特电机，2011，39（3）：17－20．

［14］ 王子辉，叶云岳．反电势算法的永磁同步电机无位置传感器自启动过程［J］．电机与控制学报，2011，15（10）：36－42．

［15］ 李文华，张宗珍．活塞压缩机电机主轴等效转动惯量的折算［J］．电机技术，2007（3）：8－10．

［16］ Boldea I，Paicu M C，Andreescu G D．Active flux concept for motion－sensorless unified AC drives［J］．IEEE Transactions on Power Electronics，2008，23（5）：2612－2618．