禁止卖空条件下跳扩散模型的均值－方差问题

李玉萍

（郑州师范学院数学与统计学院，郑州 450044）

禁止卖空条件下跳扩散模型的均值－方差问题

李玉萍

（郑州师范学院数学与统计学院，郑州 450044）

在禁止股票卖空的限制条件下讨论股价服从跳扩散过程的均值－方差投资组合选择问题.通过求解二次随机控制问题得到均值－方差问题的最优投资策略和有效前沿.

均值－方差投资组合选择；二次随机控制；最优投资策略；有效前沿

关于投资组合选择的研究可以追溯到1952年Markowitz对单时期均值－方差有效投资组合的开创性工作；后来，Duffie［1］和Grossman［2］等分别将Markowitz的工作推广到多时期和连续时间投资的组合选择模型；Li和Ng［3］又利用嵌套思想将 Markowitz均值－方差模型推广到多时期情形；Zhou和Li［4］也探讨了连续时间均值－方差问题.由于在有些金融市场中股票的交易是禁止卖空的，因此考虑禁止卖空的金融市场的投资问题更具有实际意义.为此，Li［5］，Bai［6］等分别研究了不允许股票卖空情况下的均值－方差投资组合选择问题，但是上述研究均基于股票价格是扩散模型的，而金融市场中股票价格服从跳－扩散过程更为常见，文献 ［7－10］则讨论了跳－扩散模型在金融市场中的应用.在本文中，笔者将禁止股票卖空情况下股价服从跳扩散过程时连续时间均值－方差投资组合选择问题转化为带约束的线性随机二次控制问题，但是由于交易限制的存在使得对应的Hamilton－Jacobi－Bellman方程在这种情况下没有平滑解，因此利用文献 ［11］的方法，寻求最优投资策略和有效前沿.

1 金融市场模型

市场上有d＋1种证券，其中一个无风险证券的价格P0（t）满足方程

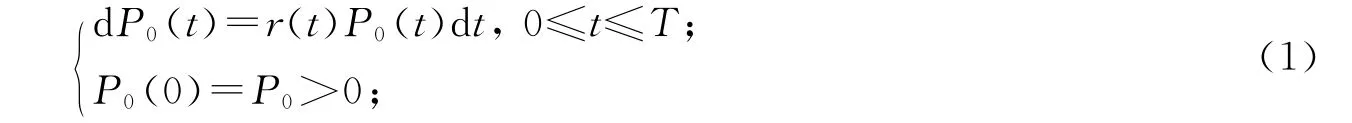
其余d种风险证券的价格P1（t），P2（t），…，P d（t）满足随机微分方程

其中i∈1，2，…，d，bi（t）（＞r（t））是预期收益率，σij（t）是波动率系数，φik（t）是股票跳跃的高度.令

假设r（t），b（t），σij（t），φ（t），λ（t）是确定的，且在［0，T］上有界.另外，还假设λ（t）＞0，［σ（t），φ（t）］非奇异.若一投资者拥有初始财富X0＞0，t≥0时刻的总财富表示为X（t），则X（t）满足

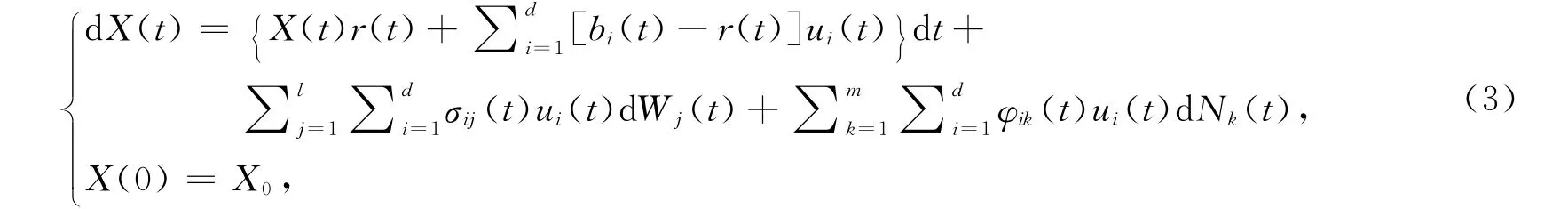
其中u（t），i＝0，1，…，d表示投资者投资在第i种资产上的货币，称u（t）＝ （u（t），…，u（t））T为一i1d个投资组合.本文考虑的一个重要限制是股票卖空的限制，即必须满足ui（t）≥0，i＝0，1，…，d.

均值 －方差投资组合选择问题为寻找一个可容许投资策略，使得EX（T）＝c，且终端财富方差varX（T）＝E［X（T）－E（T）］2＝E［X（T）－c］2最小.

由于（4）是一个凸最优化问题，所以等式限制EX（T）＝c可以通过引入一个拉格朗日乘子μ∈R来处理.这样，策略选择问题（4）可以转化为下面的随机最优化问题：

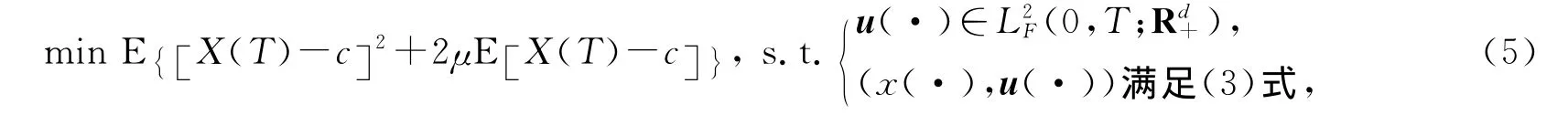
其中目标函数中拉格朗日乘子μ前面的因子2是为了方便而引入的，显然这个问题又等价于

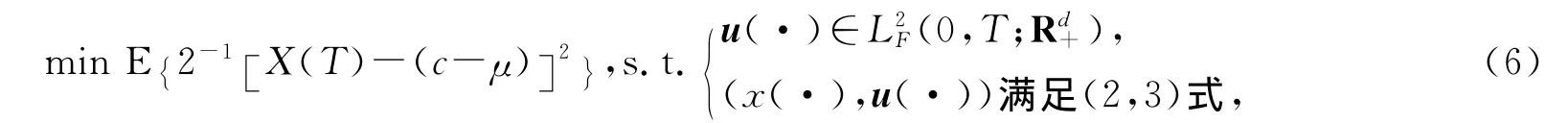
这两个问题有同样的最优控制.

2 有效策略和有效前沿

令x（t）＝X（t）－（c－μ），则问题（6）等价于

由文献［11］1635，令

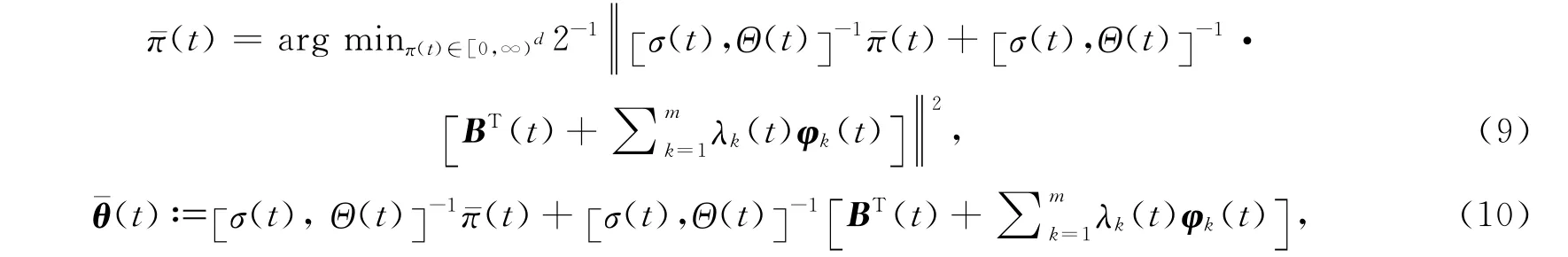
定理1 问题（5）的最优投资策略为

下面求策略选择问题（4）的有效前沿.由于E ｛2－1x2（T）｝＝ E ｛2－1［X（T）－（c－μ）］2｝＝E｛2－1［X（T）－c］｝＋μ［EX（T）－c］2＋2－1μ2，因此对于每个固定的μ，有

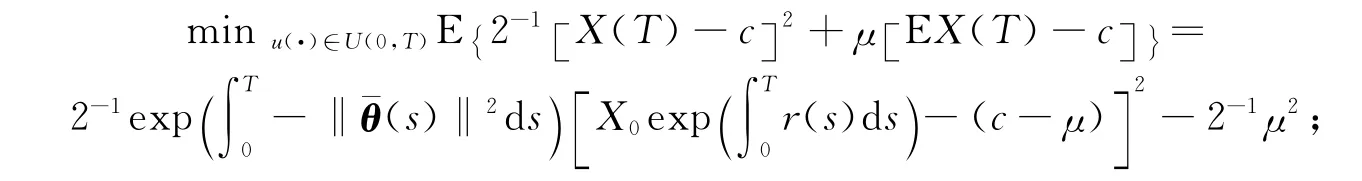
因此，在最优投资策略（11）下，问题（5）的最优值为

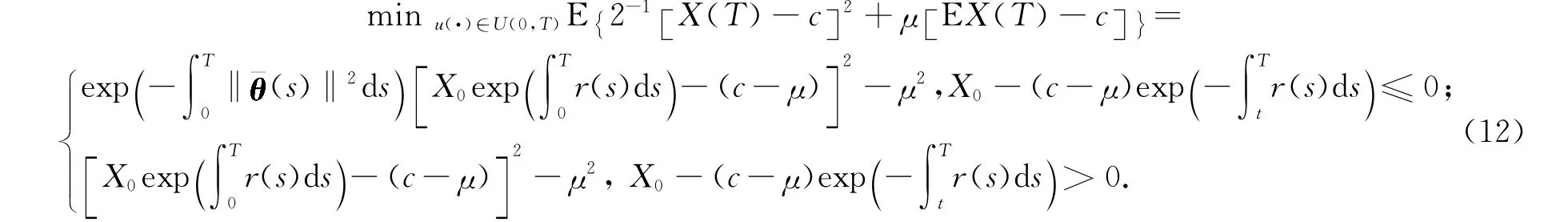
由于上面的值依赖于拉格朗日乘子μ，故为了使方差varX（T）最小，由Lagrange对偶定理，须在μ∈R上最大化（12）的值.

定理2 投资组合选择问题（4）相应于期望终端财富EX（T）＝c的有效策略为

［1］DUFFIE D，RICHARDSON H R.Mean－variance hedging in continuous time［J］.Ann Appl Probab，1991，1（1）：1－15.

［2］GROSSMAN S J，ZHOU Z Q.Equilibrium analysis of portfolio insurance［J］.J Financ，1996，51（4）：1379－1403.

［3］LI Duan，NG Wanlung.Optimal dynamic portfolio selection：multiperiod mean－variance formulation［J］.Math Financ，2000，10（3）：387－406.

［4］ZHOU X Y，LI D.Continuous－time mean－variance portfolio selection：a stochastic LQ framework ［J］.Appl Math Optim，2000，42（1）：19－33.

［5］LI Xun，ZHOU Xunyu，LIM A E B.Dynamic mean－variance portfolio selection with no－shorting constriants［J］.SIAM J Control Optim，2002，40（5）：1540－1555.

［6］BAI Lihua，ZHANG Huayue.Dynamic mean－variance problem with constrained risk control for the insures［J］.Math Meth Oper Res，2008，68（1）：181－205.

［7］SHEN Yang，SIU T K.The maximum principle for a jump－diffusion mean－field model and its application to the mean－variance problem ［J］.Nonlinear Anal：Theor Meth Appl，2013，86：58－73.

［8］MAEKAWA K，LEE S，MORIMOTO T，et al.Jump diffusion model with application to the Japanese stock market［J］.Math Comput Simulat，2008，78（2／3）：223－236.

［9］史敬涛.带Poisson跳跃的正倒向随机延迟系统递归最优控制问题的最大值原理 ［J］.中国科学：数学，2012，42（3）：251－270.

［10］王志焕，林建伟.跳－扩散模型下一类房产期权模型及计算分析 ［J］.扬州大学学报：自然科学版，2011，14（3）：23－26.

［11］PAN Yanling，CHEN Li.Stochastic liner－quadratic control problem with no－shorting constraints follow jumpdiffusion process［J］.Int J Contemp Math Sci，2012，7（33）：1633－1638.

Mean－variance optimal portfolio problems with jump－diffusion model under short－selling prohibition

LI Yuping

（Sch of Math ＆Stat，Zhengzhou Norm Univ，Zhengzhou 450044，China）

This paper deals with mean－variance portfolio selection problems when stock prices follow a jump－diffusion process under the constraint that short－selling of stocks is prohibited.Solving linear－quadratic stochastic control problem enables one to explicitly obtain the optimal investment strategies and efficient frontier for the mean－variance problem.

mean－variance portfolio selection；linear－quadratic stochastic control；optimal investment strategy；efficient frontier

O 211.6；F 830.9

A

1007－824X（2014）01－0016－05

2013－04－15.＊ 联系人，E－mail：liyuping970301＠sina.com.

河南省科技厅软科学基金资助项目 （132400410697）.

李玉萍.禁止卖空条件下跳扩散模型的均值－方差问题 ［J］.扬州大学学报：自然科学版，2014，17（1）：16－20.

（责任编辑 时 光）