一类分数阶微分方程边值问题解的存在性

裴玲燕，赵语维，董琪翔

（扬州大学数学科学学院，江苏 扬州 225002）

一类分数阶微分方程边值问题解的存在性

裴玲燕＊，赵语维，董琪翔

（扬州大学数学科学学院，江苏 扬州 225002）

对导数的阶数大于2小于3、边值非0的一类非线性分数阶微分方程的边值问题，通过构建方程的Green函数，利用非紧测度理论和相关的不动点定理，得到此类方程的解存在的条件，改进和推广了一些已有的结果.

分数阶积分；分数阶导数；微分方程；边值问题；mild解

本文研究一类非线性分数阶微分方程边值问题

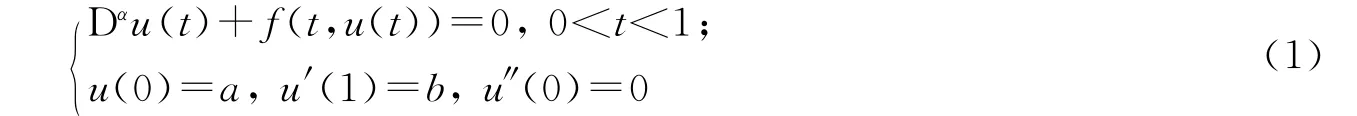
解的存在性，其中Dα表示α阶Caputo分数阶导数，α∈（2，3），f：［0，1］×R→R.

由于分数阶微积分非常适用于刻画具有记忆和遗传性质的材料及其过程，因此被越来越多地用于描述光学、热学、流变学、材料和力学系统，信号处理和系统辨识、控制及其他许多应用领域中的问题，近年来有了较丰富的研究成果［1－7］.Zhou等人在文献［3］中讨论了问题（1），利用非紧测度等理论研究了边值全为0的情形下解的存在性.在本文中，笔者拟探讨边值不全为0时非线性分数阶微分方程边值问题（1）.

1 预备知识

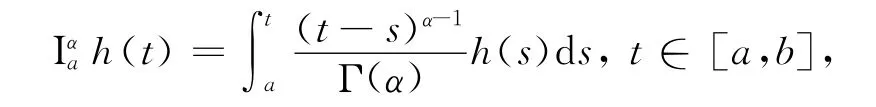
称为函数h的α阶Riemann－Liouville（分数阶）积分，也称为Riemann－Liouville分数阶积分算子，其中Γ（·）为Gamma函数.

定义2［2］27设h：［a，b］→R，α＞0，n＝ ［α］＋1，定义

定义1［2］13设h∈L1（［a，b］；R），α＞0，定义算子Iαa：L1（［a，b］；R）→C（［a，b］；R）为

称为h在t点的α阶Riemann－Liouville（分数阶）导数，也称R为Riemann－Liouville分数阶微分算子，其中［α］表示实数α的整数部分.

定义3［2］50设h：［a，b］→R，α＞0，n＝ ［α］＋1，定义

称为h在t点的α阶Caputo（分数阶）导数，也称C为Caputo分数阶微分算子.

可以证明，当α＝n为正整数时，分数阶导数Rh（t）和Ch（t）都等于整数阶导数h（n）（t）.

本文主要讨论Caputo分数阶微分方程，为方便起见，当a＝0时，记C为Dα，为Iα.

引理1［2］54若α＞0，则方程Dαh（t）＝0的解为h（t）＝C0＋C1t＋C2t2＋…＋Cn－1tn－1，其中Ci为常数，i＝1，2，…，n－1，n＝［α］＋1.进一步地，若 Dαh（t）∈L（［0，b］），则IαDαh（t）＝h（t）＋C0＋C1t＋C2t2＋…＋Cn－1tn－1.

当研究微积分方程时，非紧测度理论是一个有力的工具［8－11］.下面引入非紧测度的定义.

定义4［8］4设Y是实Banach空间，B是Y中的有界子集，且令χY（B）＝inf｛ε＞0；B在Y中被有限个半径不小于ε的球所覆盖｝，称χY（B）为B在Y中的Hausdorff非紧性测度.

非紧性测度最重要的性质在于χY（B）＝0当且仅当B在Y中相对紧.在连续函数空间中，Hausdorff非紧性测度有便于计算的表示.设C［a，b］为区间［a，b］上的连续函数全体，按上确界范数构成的Banach空间，B⊂C［a，b］为有界集，x∈C［a，b］为连续函数.本文记χC为C［a，b］中的Hausdorff非紧性测度，定义x的连续模为ω（x，ε）＝sup｛｜x（t）－x（s）｜：t，s∈［a，b］，｜t－s｜＜ε｝.进一步地，设ω（B，ε）＝sup｛ω（x，ε）；x∈B｝，ω0（B）＝limε→0ω（B，ε）.可以证明（参见文献［11］）

2 mild解的存在性

首先讨论边值问题（1）解的定义.设g∈C（［0，1］；R｝，α∈ （2，3）.考虑初值问题

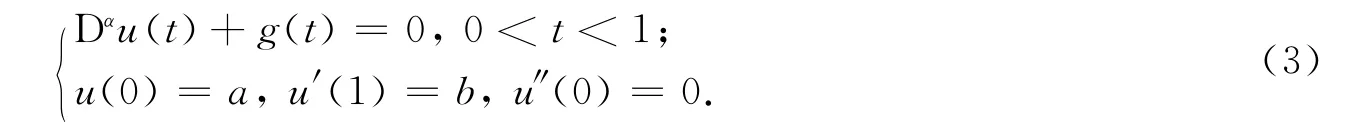
方程两边应用积分算子Iα，由引理1知，存在常数c0，c1，c2，使得

由边值条件u（0）＝a可得c0＝a.（4）式两边分别求导，可得

反之，若u∈C［0，1］是由（7）式给出，则它必满足边值问题（3），因此得到下面的命题.

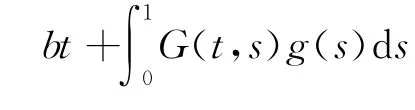
由此，可给出边值问题（1）的mild解的定义.

定义5 设α∈ （2，3），u∈C［0，1］使得u（0）＝a，u′（1）＝b，u″（0）＝0.若u满足积分方程

则称u是边值问题（1）的一个mild解，其中G由（8）式定义.

由于2＜α＜3，故由Green函数G的定义可见，G在［0，1］×［0，1］上连续，从而有界.记M＝supt，s∈［0，1］｜G（t，s）｜.对x∈C［0，1］，令 ‖x‖ ＝sup0≤t≤1｜x（t）｜，则（C［0，1］；‖·‖）为Banach空间.现给出下面的假设.

H1：f：［0，1］×R→R满足Carathedory条件，即对几乎处处的t∈ ［0，1］，f（t，·）：R→R连续，对所有u∈R，f（·，u）：［0，1］→R可测；

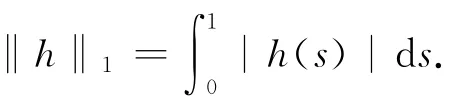
定理1 若H1，H2成立，则边值问题（1）至少有一mild解.

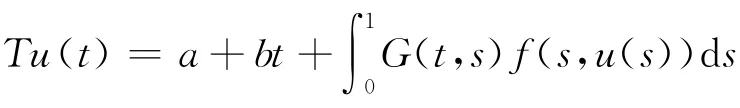
现设u∈C［0，1］，0≤t1＜t2≤1，则

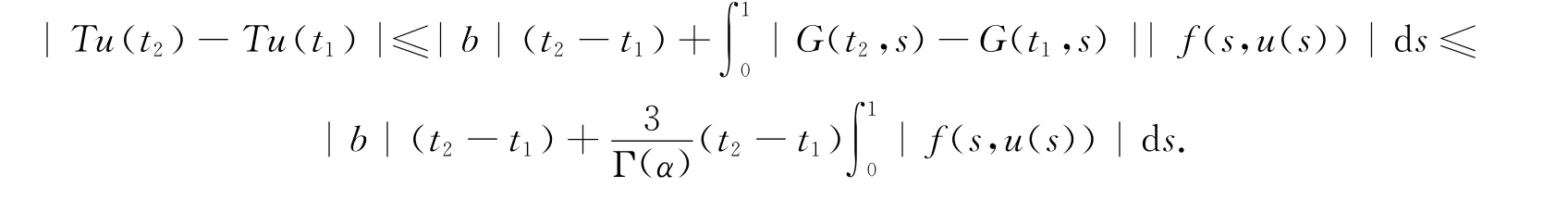
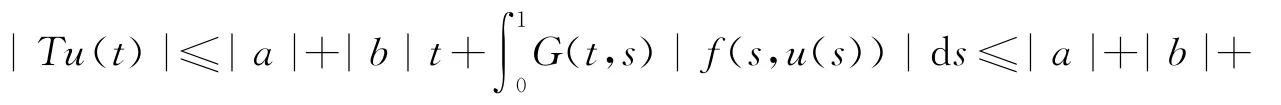
最后，由Schauder不动点定理知T在W中有不动点，即边值问题（1）有mild解.定理证毕.

当f连续时，条件H1自然成立，因此类似地可得如下定理.

定理2 若f：［0，1］×R→R连续，且H2成立，则边值问题（1）至少有一mild解.

3 应用

例1 考虑分数阶边值问题

［1］RASHID M H M，AL－OMARI A.Local and global existence of mild solutions for impulsive fractional semilinear integro－differential equation［J］.Commun Nonlinear Sci Nuner Simulat，2011，16（9）：3493－3503.

［2］DIETHELM K.The analysis of fractional differential equations：an application－oriented exposition using differential operators of Caputo type［M］.Berlin：Springer，2010：13－65.

［3］ZHOU Wenxue，PENG Jigen.Existence of solutions to boundary value problem for fractional differential equation［J］.Chin J Eng Math，2011，28（6）：727－735.

［4］BAJLEKOVA E G.Fractional evolution equations in Banach space［M］.Eindhoven：University Press Facilities，2001：1－18.

［5］LAKSHMIKANTHAM V，VATSALA A S.Basic theory of fractional differentional equation［J］.Nonlinear Anal：Theor Meth Appl，2008，69（8）：2677－2682.

［6］ZHANG Shuqin.The existence of a positive solution for a nonlinear fractional differential equation［J］.J Math Anal Appl，2000，252（2）：804－812.

［7］董琪翔，毋光先，李姣.Banach空间中一类分数阶微分方程边值问题 ［J］.纯粹数学与应用数学，2013，29（1）：1－10.

［8］郭大钧.非线性分析中的半序方法 ［M］.济南：山东科学技术出版社，2000：1－13.

［9］徐小平，毋绪道，王杰瑛，等.Banach空间中一类无穷时滞分数阶微分方程 ［J］.扬州大学学报：自然科学版，2012，15（4）：16－19，29.

［10］DONG Qixiang，LI Gang.Existence of solutions for semilinear differential equations with nonlocal conditions in Banach space［J］.Electr J Quali Theory Diff Equati，2009，47：1－13.

［11］BANA J，GOEBEL K.Measures of noncompactness in Banach spaces［M］.New York：Marcel Dekker Incorporated，1980：60－75.

Existence of solutions to a class of boundary value problem of fractional differential equations

PEI Lingyan＊，ZHAO Yuwei，DONG Qixiang

（Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China）

This paper is concerned with a class of nonlinear fractional derivative equations with boundary value conditions，where the order of fractional differential is greater than 2 and less than 3，and the boundary values are not all zero.By using the Green’s function，the theory of measure of noncompactness and fixed point theorem，the conditions for the existence of mild solutions are obtained.It improves and generalizes some previous results.

fractional order integral；fractional order derivative；differential equation；boundary value problem；mild solution

O 175.15

A

1007－824X（2014）01－0005－04

2013－06－14.＊ 联系人，E－mail：1184699162＠qq.com.

国家自然科学基金资助项目（11271316，11201410）；扬州大学大学生科技创新基金资助项目（B12010）.

裴玲燕，赵语维，董琪翔.一类分数阶微分方程边值问题解的存在性 ［J］.扬州大学学报：自然科学版，2014，17（1）：5－8.

（责任编辑 时 光）