大学物理教学中的类比法探讨

王春芳

（上海理工大学 物理系，上海 200000）

大学物理教学中的类比法探讨

王春芳

（上海理工大学 物理系，上海 200000）

本文通过介绍运类比法组织教学的典型例子，说明在物理教学中，应用类比法对提高教学质量、培养创造能力都具有重要的现实意义。

大学物理；类比法；教学

作为一门自然科学的基础课程，很多学校都将大学物理作为专业必修课开设。大学物理涉及物理学的基本概念、理论和方法，这些知识是构成学生科学素养的重要组成部分，同时，也是高新技术理论重要基础。通过对该课程的学习，可以培养学生的科学世界观，增强学生分析问题和解决问题的能力，培养学生的探索和创新精神。然而，随着我国高等教育扩招规模的快速发展，办学规模不断扩大，这使得普通高等院校学生基础出现了一定程度的下降，因此，在大学物理教学中出现许多新的问题。比如说，学生反映物理难学，老师觉得难教，很多同学缺乏学习兴趣，甚至许多学生通过死记硬背来应付考试。即便如此，期末考试学生的挂科率也比较高，这给大学物理课程教学目标的实现带来了很大难题。为了解决物理教学中的这些问题，除了教学的深度改革之外，还需要教师掌握有效的教学方法，提高教学质量。其中，类比法就是一种可以有效地缓解工科大学物理课程内容多、学时紧的矛盾，而且可以帮助学生在学习中举一反三、融会贯通。

结合笔者的教学实践，本文就物理教学和学习中经常使用的类比法作一些探讨。

所谓类比，就是指运用特定事物在某些方面的相同、相似或可比拟的特性来分析、推断所研究对象在另一些方面的属性和特征的一种间接推理方法。

在物理学的发展历史上，有一些著名的物理学家就是运用类比推理的方法取得成功的。如荷兰物理学家惠更斯，他发现光和声这两类物理现象具有很多相同的性质：它们都遵循直线传播规律，都有反射、折射和干涉现象，而“声”是一种波动，由此他推出结论：“光”可能也是一种波动，随后的很多实验证明，这种类比推理得出的想法是正确的。又如，20世纪20年代，法国著名青年物理学家德布罗意就是在将实物粒子与光子进行类比的基础上，得出了“实物粒子也具有波动性”这一物理学史上具有划时代意义的科学论断。还有，轨道量子化中，自旋量子数的得出，都是类比推论的结果。

从事大学物理教学的教师都会体会到：类比法不仅是一种重要的科学研究方法，也是一种有效的教学方法。尤其对工科大学物理的教学而盲，教学内容中的很多概念都可以通过相互类比进行学习和理解。例如，力学中质点的直线运动公式、刚体的定轴转动公式，以及量子力学中的各种力学关系，都可以进行类比；电磁学中静电场规律与稳恒磁场规律的类比等。在教学中适当地运用类比法，不仅可以帮助学生在学习中举一反三、融会贯通，而更为重要的是，通过这样的教学实践，可以培养学生善于观察、勇于探索的科学能力。

下面举几个运用类比法进行物理教学的典型例子。

康普顿效应和光电效应，都是表明光的粒子性的两个重要效应。康普顿效应是光子与电子发生弹性碰撞，而光电效应则是电子吸收光子。为什么会产生这样的区别？同样是用光子去打击电子，为什么用可见光照射时，电子可以吸收光子，表现为光电效应；而用X射线照射时，此时电子不吸收光子，而是与光子发生弹性碰撞，表现为康普顿效应？它们之间会有什么联系呢？带着这些疑问，我们将这两种效应进行一场深入的对比和分析。

在光电效应中，入射光通常是可见光和紫外光，这些光子的能量很低，大约为几个eV，和金属中电子的束缚能量（逸出功）有相同数量级。所以，在光电效应中，光子和物质相互作用时，必须考虑光子、电子和原子核三者的能量和动量变化．但是，由于原子核的质量比电子大几千倍，因此，核的能量变化很小，可以忽略不计，而动量变化较大，无法略去。爱因斯坦方程只表示光子与电子的能量守恒，而没有相应的光子和电子的动量守恒关系。

而在康普顿效应中，X射线光子的能量大约在10～10eV，相对于光电效应的入射光而言，能量大了很多。此时，可认为是光子与核外电子二者的相互作用，光子和电子之问能量和动量均守恒，而没有考虑原子核的运动。作为一级近似，可以认为电子是自由的。光子与这种“自由电子”发生碰撞，损失部分能量出射，宏观体现为波长变长。与光子作用的那个电子叫做康普顿电子（初速度为零），康普顿电子获得光子给予它的那部分能量出射． 其出射角度在0°～90°之间，这也证明了康普顿效应是两个准自由粒子的弹性碰撞。

此外，薄膜干涉中的等倾干涉条纹与牛顿环很容易混淆，教学的过程中，可以通过类比的方法将它们予以区分，加深理解和记忆。首先，可以告诉学生，等倾干涉产生于平行薄膜干涉，而牛顿环产生于楔角渐变的薄膜干涉。其次，可根据它们的产生原理不同，分析条纹的特点。如图1所示，对等倾干涉而言，假设薄膜光学厚度为nh，入射角为i，对应折射角为γ，此时光程差为

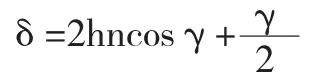
由上式可知，γ相等（即入射角i相等）的点，光程差相等，这些点形成同一圆形条纹，当然，不同的入射角具有不同级次的同心圆环。i越小光程差越大，干涉级次越高，即圆环中心（i=0）的级次最高。

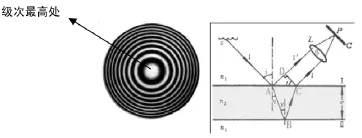
图1 平行薄膜的等倾干涉

对牛顿环而言，如图2所示，垂直下表面入射角的单色光在厚度为h处的光程差为：

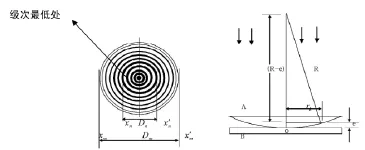
图2 楔形薄膜干涉

由此可见，厚度h相同处光程差相等，即同一厚度的所有点具有同一级干涉条纹，因此，干涉条纹也是圆形的，e不同时，构成一系列同心圆环。e越小，光程差越小，干涉级次越低，即e=0时，级次最低。

类比法在物理教学中的运用相当广泛，它不仅有利于学生对新知识的学习、理解，还有利于对较复杂的物理过程和抽象物理概念的具体化、形象化，能帮助学生通过联想进行再造想象，寻求思维的线索，获取解决问题的方法。对于培养学生创造能力具有重要的现实意义。

[1]Compton A H.A quantum theory of the scattering of X-rays by light elements[J].Physcal Review，1923，21（5）：483-502.

[2]Compton A H.The spectrum of scattered X-rays[J].Physcal Review，1923，22（5）：409-413.

[3]姚启钧.光学教程[M].北京：人民教育出版社，1981.

G642.41

A

1674-9324（2014）20-0071-02