基于FAHP和模糊综合评判的高职数学教师素质评价研究
2014-05-25蒋沈庆
蒋沈庆
(南通航运职业技术学院 基础教学部,江苏 南通226010)
众所周知,高等数学在整个高职教育阶段,不仅是学习其他课程的基础,而且还是整个高职教育的基础,甚至是终身教育的一个基础。提高学生的数学素质,逐步将所学数学知识转化以达到高职院校培养应用型人才的目标。因此,高职数学教师在整个高等职业教育过程中充当了很特殊的角色,同时数学教师接触的学生较多,也较为广泛,可以说所有的专业都要开设至少一年的数学课程,可见高职数学教师的影响之大。因此,提高高职数学教师素质是提高高等职业教育的质量保证。只有建立起科学有效的高职数学教师评价制度,才能使高职数学教师师资队伍自身素质不断提高,才能充分挖掘教师的潜能,发挥数学教师在高职教育发展中的作用。本文首先构建高职数学教师素质评价指标体系,采用模糊层次分析法(FAHP)确定指标权重,再采用模糊综合评判得到评价对象综合素质各方面的评价信息,为现阶段高职数学师资队伍建设提供一个简便可行的评价体系。
1 高职数学教师素质评价体系
1.1 构建高职数学教师素质评价指标体系
高职数学教师综合素质评价指标的确立是一个复杂而系统工作,必须要筛选出能够全方位、多角度反映高职数学教师素质的评价指标。本文综合、补充文献[1-2]的研究结果,按照科学、全面、简明、可行原则,设计了高职数学教师素质评价指标体系。
1.2 用模糊层次分析法(FAHP)确定各指标权重
模糊层次分析法(FAHP)是先通过同层元素两两比较建立模糊互补判断矩阵。设存在指标集B={b1,b2,…,bn},采用表1进行标度,且满足aij=1- aji,其中aij表示指标因素ui比uj重要的隶属度,aij越大,表示ui比uj越重要,则所构建的判断矩阵A=(aij)n×n是模糊互补判断矩阵。对模糊互补矩阵A=(aij)n×n按行求和,记,并施数学变换则矩阵R=(rij)n×n是模糊一致矩阵,即不用再去检验矩阵的一致性。然后对矩阵R 采用行和归一化求得的排序向量w=(w1,w2,…,wn)T,满足
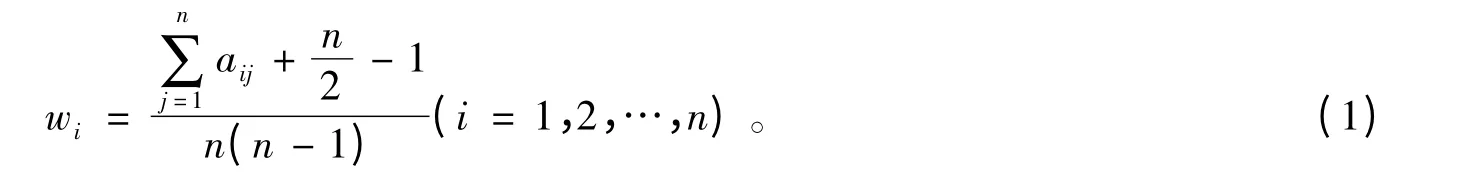

表1 FAHP 中0.1~0.9 标度含义
1.3 用模糊综合评判进行综合评价
模糊综合评判是在考虑与被评价对象相关的各种因素的影响下,运用模糊数学工具对被评价对象做出合理的综合评价。设因素集为与被评价对象相关的m 种因素,记作U={u1,u2,…,um},评语集为所有可能出现的n 评语,记作V={v1,v2,…,vn}。记tij为因素ui(i=1,2,…,m)具有评语vj(j=1,2,…,n)的程度,构造综合评价矩阵T=(tij)m×n。
确定评价对象的指标由m 个因素决定,其因素为U,U={u1,u2,…,um},每个因素的重要程度系数记为wi,即它们的权重是不同的,权重的分配是因素U 上的一个模糊子集W,W={w1,w2,…,wm},其中wi为因素集中ui的权重值,wi≥0,且
然后通过复合运算求出综合评价结果B=W·T=(b1,b2,…,bn),其中bj表示被评价对象具有评语vj的隶属度。再从最大隶属度原则出发,在B=(b1,b2,…,bn)中取其最大值作为被考评对象所获得的等级。
2 高职数学教师素质评价
2.1 运用FAHP 求高职数学教师素质评价指标的权重
根据图1层次结构模型,将某一层次的指标相对上一层次指标按重要程度进行两两比较,得模糊互补判断矩阵,指标两两比较的重要程度按表1来确定。然后将某一层次指标相对于上一层次指标的重要程度进行排序,得出各指标之间的相对权重。具体数据如下:

表2 总目标层高职数学教师素质评价的模糊互补判断矩阵及权重

表3 准则层U1 的模糊互补判断矩阵及权重
同理可得U2、U3、U4的模糊互补判断矩阵及权重,结果如下:
w2=(0.15,0.2,0.235,0.235,0.18)
w3=(0.1767,0.1567,0.2033,0.1467,0.19,0.1267)
w4=(0.2417,0.2083,0.2667,0.2833)
2.2 运用模糊综合评判对高职数学教师素质进行评价
2.2.1 高职数学教师素质一级指标模糊评价
第一,采用专家调查法开展评判工作。由领导、专家、学生、教师等共同组成专家组,根据各指标包含的具体评价要求,给出评语集V={优秀,良好,一般,较差}。
第二,确定综合评价矩阵,即确定准则层Ui与V 之间的关系矩阵,以U1为例。假设U11=(0.6,0.4,0,0),U12=(0.5,0.4,0.1,0),U13=(0.4,0.4,0.2,0),如U12的含义是:在这个评估专家组中有50%的成员认为该教师职业道德是优秀的,40%的成员认为良好,10%的成员认为一般,没有人认为较差。构造U1与V 之间的关系矩阵T1:

第三,一级指标模糊评价。根据前面计算出的U1层指标权重向量w1,通过B1=w1·T1计算得到U1层次综合评价:

即专家组认为该教师在思想政治素质方面有52%的人认为优秀,有40%的人认为良好,8%的人认为一般,没有人认为较差,从最大隶属度原则出发,取其最大值作为被考评对象所获得的等级,评定为:优秀。同理可得:B2=(0.28 0.36 0.30 0.06 ),评定为:良好;B3=(0.36 0.40 0.20 0.03 ),评定为:良好;B4=(0.34 0.36 0.23 0.08 ),评定为:良好。
2.2.2 高职数学教师素质二级模糊评价
一级指标的模糊评价仅仅显示教师单项指标的评价,利用求得的一级指标权重w0,一级模糊评价矩阵

通过B=w0·T0计算得到目标层综合评价结果为:B=(0.37 0.38 0.21 0.04 ),评定为:良好。若依据现实生活中的评价等级标准:优秀(100~90 分)、良好(90~80 分),一般(80~60 分),较差(60~0 分),可取等级评价矩阵V=(95 85 70 50),所以该教师的素质评价分数为:0.37×95+0.38×85+0.21×70+0.04×50=83.9,即可求出高职数学教师素质评价的定量分数。
3 结 语
本文从思想政治素质、科学文化素质、职业道德素质、科研素质等四个方面构建高职数学教师素质三层评价指标体系,通过模糊层次分析法确定高职数学教师素质评价指标,综合多位专家的经验知识,从而保证评价结果的客观、准确与公正,并且该方法直接由原模糊互补判断矩阵求出较为理想的排序向量,计算结果简洁、合理、有效。再运用模糊综合评判对评价数据自底向上逐层处理,得出高职数学教师素质各方面的评价结果。对某个教师的评价实例证明模糊层次分析法与模糊综合评判相结合的评价模型简便、可行,结果合理,可大面积推广。
[1]张德全.谈高职高专院核毅营教师的素质拓展[J].桂林航天工业高等专科学校学报,2007,46(2):73-76.
[2]冯素芬.论高职数学教师的素质[J].北京工业职业技术学院学报,2003,2(1):59-61.
[3]张吉军.模糊层次分析法(FAHP)[J].模糊系统与数学,2000,14(2):80-88.
[4]徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314.
[5]陈水利,李敬功,王向公.模糊集理论及其应用[M].北京:科学出版社,2005.
