金属橡胶隔振系统动刚度及减振效能分析
2014-05-25赵国伟李德勇
赵国伟,李德勇,陈 勇
(北京航空航天大学宇航学院,北京 100191)
金属橡胶隔振系统动刚度及减振效能分析
赵国伟,李德勇,陈 勇
(北京航空航天大学宇航学院,北京 100191)
基于圆柱螺旋弹簧受压变形原理建立金属橡胶隔振系统动力学模型。分析在简谐激励作用下金属橡胶的动态刚度、频率响应及减振特性。基于谐波平衡法分别获得激励频率对金属橡胶压缩量幅值影响及金属橡胶压缩量幅值与激励频率对金属橡胶动态刚度影响。通过分析金属橡胶隔振系统获得金属橡胶构件高度、工作面横截面积及激励频率对冲击隔离系数影响,推导的冲击隔离系数表达式对金属橡胶设计及工程实际应用有重要指导意义。
金属橡胶;动力学模型;动态刚度;频率响应;冲击隔离系数
随工程界对在冲击振动环境中工作系统性能要求的不断提高,作为新型基于干摩擦耗能机理非线性隔振材料的金属橡胶颇受重视。金属橡胶由一定质量的螺旋金属丝经有序编织后置于模具中冲压而成,为均匀弹性多孔材料,具有高弹性、大阻尼、耐高温、耐高压、耐高真空及耐腐蚀性等特点。金属橡胶受振动激励或冲击时其内部螺旋金属丝会发生弹性变形,该变形达到临界值时金属丝之间开始接触,继而发生摩擦、挤压并耗散大量能量。由微元弹簧变形建立的金属橡胶力学模型[1-5]通过静力学或动力学实验获得金属橡胶力学模型或相关参数变化对金属橡胶减振性能影响;但对金属橡胶隔振系统的动态刚度及减振效能研究较少。本文基于金属橡胶隔振系统动力学模型,研究在简谐激励作用下隔振系统动态刚度、频率响应及冲击隔离系数等特性。
1 金属橡胶力学建模
1.1 金属橡胶构件力学模型
金属橡胶构件据微观结构特征可视为将具有一定数量的圆柱螺旋微元弹簧按一定规律排列组合而成。振动激励下金属橡胶内部微元弹簧主要承受轴向、径向载荷作用,且微元弹簧变形也主要由于金属丝截面承受弯矩、扭矩引起。
1.1.1 金属微元弹簧刚度分析
由于圆柱形微元弹簧受载荷作用时轴向、径向表现的刚度不同,设变形过程中微元弹簧仍基本保持螺旋形,可建立微元弹簧轴向、径向刚度模型。
1.1.1.1 圆柱螺旋微元弹簧受轴向载荷作用
弹簧受轴向压缩载荷Fz作用后,据文献[6]可得微元弹簧沿轴向载荷方向变形为
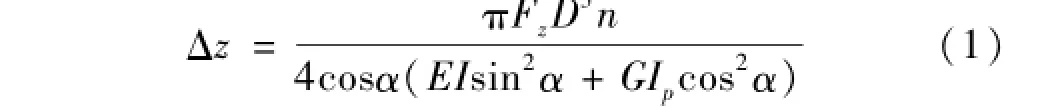
式中:α为螺旋角;D为微元弹簧中径;n为微元弹簧螺旋圈数;G为金属丝材料切变模量,对各向同性材料G=E/[2(1+ν)],E为金属丝材料弹性模量,d为金属丝径,ν为泊松比;I=πd4/64,Ip=πd4/32分别为微元弹簧材料截面惯性矩及极惯性矩。

令式(1)中n=1得单圈微元弹簧沿轴向变形刚度为式中:β为变量(β≤1),与金属橡胶构件金属丝材料、压缩变形量及铺层排列方式等有关为金属橡胶构件相对密度,ρmr为金属橡胶构件密度,ρs为金属丝密度;a,b为与金属橡胶材料相关常数,由试验确定,A1=1/(ab),A2=1/(ab2),A3=1/(ab3)。
1.2 金属橡胶构件内部阻尼粘性等效
由于金属橡胶材料内部阻尼的复杂性及非线性,导致阻尼、刚度在一定程度上耦合,较难在金属橡胶的阻尼中区分出刚度系数。因此需从金属橡胶复刚度、复弹性模量出发分析金属橡胶材料内部阻尼。
迟滞回线能反映系统能量耗散,可对阻尼耗能进行定量分析。由于金属橡胶材料内部金属丝间干摩擦作用,激振力与金属橡胶的动态压缩量均按简谐振动规律变化时,大量实验表明应力较应变超前一个常数相位角θ,则金属橡胶的复刚度[7]为
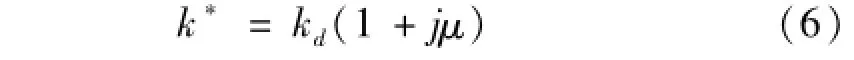
式中:kd为金属橡胶动态刚度;μ=E″/E′=tanθ为损失系数,E′为储存模量,E″为损失模量。
由式(6)及金属橡胶构件压缩量x=X sin(ωt)可得金属橡胶迟滞恢复力在每周期的能量耗散为迟滞回线围成的椭圆面积,见图1,动态刚度kd为直线PQ斜率,图中
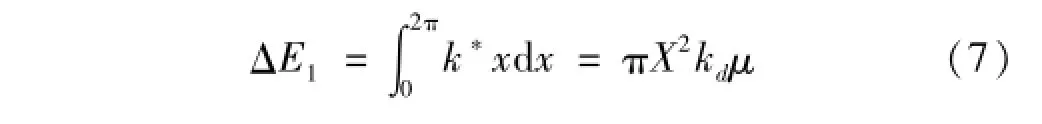
设金属橡胶材料内部等效粘性阻尼系数为ceq,则等效后的粘性阻尼在一个周期的内耗散能量可由无阻尼振动规律近似求出[8],即

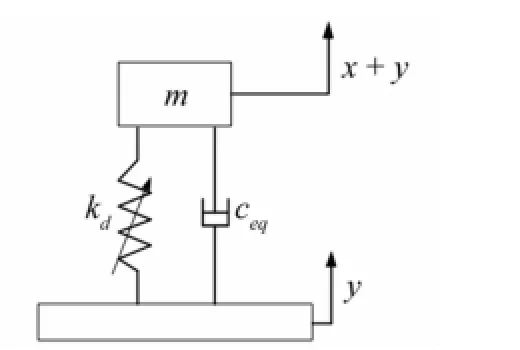
图2 金属橡胶动态简化模型Fig.2 Dynamicsmodel of isolation system formetal rubber
1.3 金属橡胶隔振系统动力学模型
金属橡胶动态模型可用高阶非线性刚度与等效粘性阻尼力叠加方法构造[10]。金属橡胶动态模型见图2。分析金属橡胶隔振系统受力可得隔振系统动力学模型为
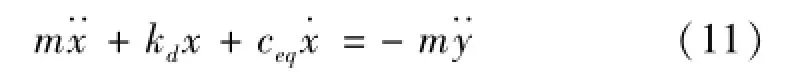
2 金属橡胶隔振系统动态刚度分析
文献[11]将金属橡胶隔振系统动态刚度描述为常数项与压缩量的二次项之和,反映金属橡胶隔振系统动态刚度与实验测试结果一致。将ε=x/h代入式(5)有
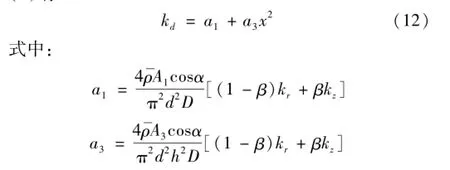
由1.2节知,简谐振动作为动态载荷作用于金属橡胶构件时激励作用力较金属橡胶压缩位移超前一个相位角θ。令激励位移y=Y cos(ωt)、压缩位移x=X cos(ωt-θ)及kd=a1+a3x2代入式(11)得
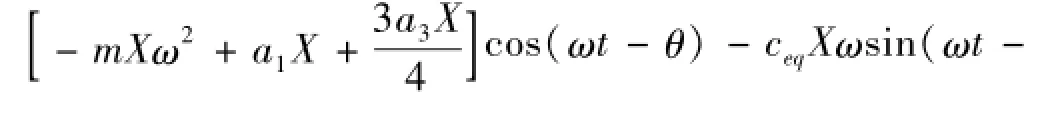

由式(16)可得金属橡胶隔振系统动态刚度与激励频率间关系,见图3。由图3看出,在相同激励频率下金属橡胶隔振系统动态刚度随压缩量幅值增大而增大;在相同压缩量幅值下其动态刚度随激励频率增大小幅减小。
3 金属橡胶隔振系统频率特性及减振效能分析
3.1 金属橡胶隔振系统频率响应特性分析
令激励位移为y=Y cos(ωt),压缩位移为x=X cos(ωt-θ),kd=a1+a3x2,并将式(9)、(10)代入式

由式(12)知,金属橡胶构件在压缩过程中高度不断减小,导致动态刚度kd中二次项系数a3不断增大。高度15 mm金属橡胶构件压缩到8 mm时(高度为15.5 mm金属橡胶构件以50 mm/min定速压缩时,最大非破坏性压缩量为7 mm[13]),a3值将由7.75×1012增加到2.7×1013,见图4。

图3 金属橡胶动态刚度kd与激励频率ω关系图Fig.3 Relationship between dynamic stiffness and excitation frequency ofmetal rubber
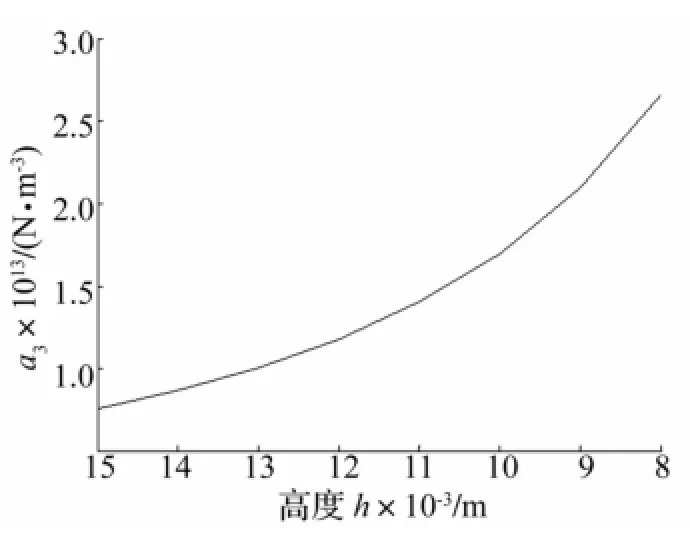
图4 动态刚度二次项系数a3与高度h之关系Fig.4 Relationship between a3and the height
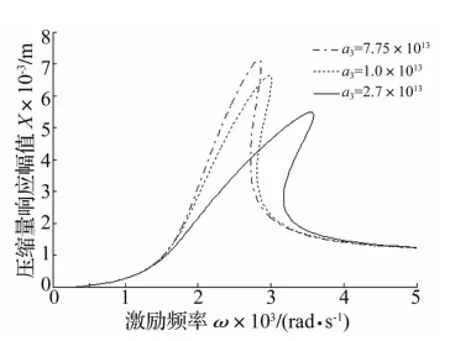
图5 金属橡胶频率响应曲线Fig.5 Amplitude-frequency response ofmetal rubber
式(19)取ξ=0.157,Y=1 mm,金属橡胶频率响应曲线见图5。由图5看出,激励频率增大时金属橡胶构件压缩量响应幅值随之增大;激励频率接近金属橡胶隔振系统动态刚度对应的固有频率时达最大值;激励频率继续增大,金属橡胶压缩量响应幅值随之下降。压缩中随金属橡胶构件高度不断减小金属橡胶压缩量响应幅值峰值减小,且峰值逐渐右移,表明金属橡胶隔振系统动态刚度对应的固有频率随金属橡胶动态刚度二次项系数增大逐渐增大。峰值右移时发生倾斜,激励频率增大到响应峰值时曲线发生跳跃现象,主要因金属橡胶构件压缩中金属丝间相互挤压摩擦的阻尼为干摩擦阻尼,压缩量达到峰值时金属丝间产生滑移现象,导致曲线在响应峰值时出现跳跃现象。
3.2 金属橡胶隔振系统减振效能分析
通常用冲击隔离系数η作为衡量金属橡胶隔振系统减振效能指标。冲击隔离系数η指响应幅值与激励幅值比值,由图2可得

激励频率与幅值确定时,为保证目标设备安全,需将冲击振动幅值降低到一定范围内。取目标设备安全临界振动冲击隔离系数η0,则在冲击隔离系数η≤η0范围内设备均安全。

取参数m′=18.6 g,ρs=7.8 g/cm3。由式(24)得金属橡胶横截面积S与高度h分别与冲击隔离系数η之关系见图6~图8。由图6看出,金属橡胶质量一定时冲击隔离系数随金属橡胶轴向横截面积增大而减小;轴向横截面积相同时激励频率越大减振系统冲击隔离系数越小,减振效果越好。由图7看出,金属橡胶质量一定时冲击隔离系数随金属橡胶高度增大而减小;高度相同时激振频率越大,减振系统冲击隔离系数越小,减振效果越好。由图8看出,对所选金属橡胶构件,激励频率增大时金属橡胶隔振系统冲击隔离系数随之增大;激励频率接近金属橡胶隔振系统动态刚度对应的固有频率时冲击隔离系数达最大值;随激励频率继续增大冲击隔离系数随之下降;金属橡胶构件压缩量增大时金属橡胶隔振系统冲击隔离系数峰值逐渐右移。
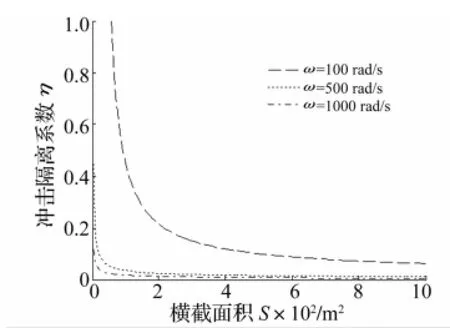
图6 冲击隔离系数η与横截面积S之关系图Fig.6 Relationship between shock isolation coefficient and cross-sectional area ofmetal rubber
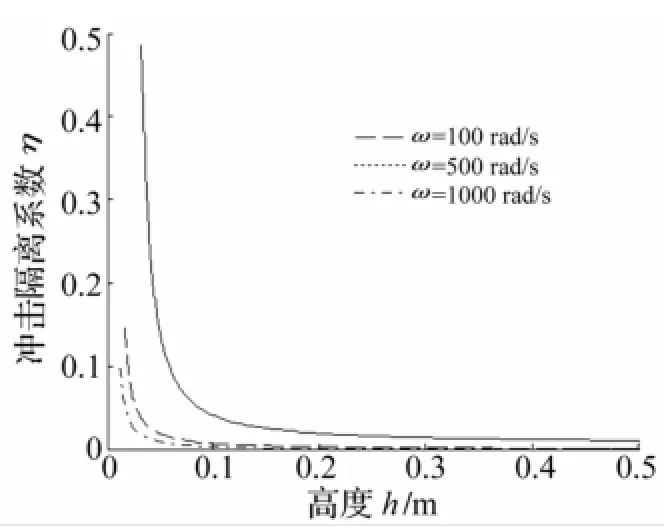
图7 冲击隔离系数η与高度h之关系Fig.7 Relationship between shock isolation coefficientand the height ofmetal rubber
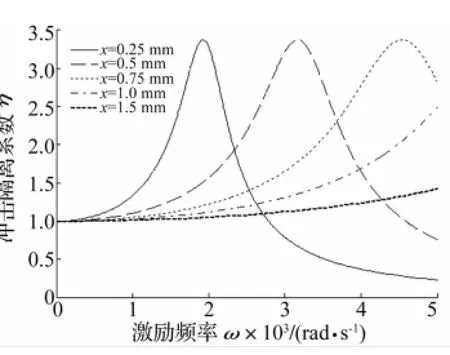
图8 冲击隔离系数η与激励频率ω之关系Fig.8 Relationship between shock isolation coefficient and excitation frequency ofmetal rubber
对任意压缩量的金属橡胶构件存在有效激励频率阈值,激励频率大于阈值时冲击隔离系数小于1,且随激励频率增大有逐渐趋近零的趋势。规律说明,对一定压缩量的金属橡胶构件而言,仅当激励频率大于激振频率阈值时才具有减振作用,且激励频率越大减振效果越明显。即金属橡胶隔振系统动态刚度越高,隔振系统对高频范围内激励的减振作用越好;对中低频段激励需选动态刚度较低的金属橡胶隔振系统,如选截面积较小、高度较大的金属橡胶构件等。
4 结 论
本文基于所建金属橡胶隔振系统动力学模型,对其动态刚度及减振效能进行仿真分析,结论如下:
(1)轴向受压且压缩量幅值相同时金属橡胶隔振系统动态刚度随激励频率增大而小幅减小;激励频率相同时金属橡胶动态刚度随压缩量幅值增大而增大。金属橡胶构件压缩过程中随压缩量的增大其动态刚度二次项系数逐渐增大,导致响应压缩量幅值峰值逐渐变大。
(2)金属橡胶隔振系统冲击隔离系数η与金属橡胶构件沿轴向横截面积S、高度h及激励频率ω有关。金属橡胶构件质量一定时η随S、h增大而减小;η随ω增大而增大,激励频率接近金属橡胶隔振系统动态刚度对应的固有频率时η达最大值;随激励频率继续增大η随之下降;属橡胶构件压缩量增大时金属橡胶隔振系统动态刚度对应的固有频率增大;金属橡胶隔振系统动态刚度对η影响较大,动态刚度较高时对高频范围内激励减振作用较好;对中低频段激励而言,选动态刚度较低的金属橡胶构件对系统减振较有益。
[1]彭威,白鸿柏,郑坚,等.金属橡胶材料基于微弹簧组合变形的细观本构模型[J].实验力学,2005,20(3):455-462.
PENG Wei,BAI Hong-bai,ZHENG Jian,et al.A micromechanics constitutive model of the metal rubber materials based on the radial and axial combined deformation of themicrosprings[J].Journal of Experimental Mechanics,2005,20(3):455-462.
[2]李宇明,彭威,白鸿柏,等.金属橡胶材料宏观和细观力学模型[J].机械工程学报,2005,41(9):38-41.
LI Yu-ming,PENG Wei,BAI Hong-bai,et al.Mechanical model ofmetal rubbermaterial inmacro and micro level[J].Chinese Journal of Mechanical Engineering,2005,41(9):38-41.
[3]许建东,郭宝亭,朱梓根,等.金属橡胶材料的振动特性[J].航空动力学报,2004,19(5):619-622.
XU Jian-dong,GUO Bao-ting,ZHU Zi-gen,et al.The vibration performance ofmetal-rubbermaterial[J].Journal of Aerospace Power,2004,19(5):619-622.
[4]金鸣,薛前光,田立强,等.金属橡胶减振器振动及冲击特性实验研究[J].电子产品可靠性与环境试验,2012,30(2):20-23.
JIN Ming,XUE Qian-guang,TIAN Li-qiang,et al.Experimental study on vibration and shock characteristics of metal rubber damper[J].Electronic Product Reliability and Environmental Testing,2012,30(2):20-23.
[5]洪杰,朱彬,马艳红,等.金属橡胶颗粒静态特性试验[J].北京航空航天大学学报,2012,38(2):218-221.
HONG Jie,ZHU Bin,MA Yan-hong,et al.Experiments on static characteristics ofmetal rubber particles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(2):218-221.
[6]张英会,刘辉航,王德成.弹簧手册第二版[M].北京:机械工业出版社,2008:281-294.
[7]比尔兹C F,著.朱世杰,陈玉琼,译.结构振动分析[M].北京:中国铁道出版社,1988:30.
[8]刘延柱,陈文良,陈立群.振动力学[M].北京:高等教育出版社,1998:13.
[9]李宇燕,黄协清.金属橡胶材料阻尼性能的影响参数[J].振动、测试与诊断,2009,29(1):23-26.
LI Yu-yan,HUANG Xie-qing.The influence of damping performance ofmetal rubbermaterial parameters[J].Journal of Vibration.Measurement&Diagnosis,2009,29(1):23-26.
[10]李宇明,郑坚,白鸿柏.金属橡胶材料的动态力学模型[J].材料研究学报,2009,17(5):500-504.
LI Yu-m ing,ZHENG Jian,BAI Hong-bai.Dynamic mechanics model of metal-rubber materials[J].Chinese Journal of Materials Research,2009,17(5):500-504.
[11]黄晓琼,李莹,张瑾瑾,等.非线性因素对金属橡胶减振系统幅频特性的影响[C].力学与工程应用(第十三卷),2010.
[12]王光远,郑钢铁,韩潮.金属橡胶动力学建模的频域方法[J].宇航学报,2008,29(2):499-504.
WANG Guang-yuan,ZHENG Gang-tie,HAN Chao.Dynamic modeling method of metallic rubbers in frequency domain[J].Journal of Astronautics,2008,29(2):499-504.
[13]李宇明,郑坚,白鸿柏,等.金属橡胶构件的拉-压变形测试[J].宇航学报,2004,18(S):51-54.
LIYu-ming,ZHENG Jian,BAI Hong-bai,et al.Stretchcompress measurement of metal rubbers specimen[J].Journal of Astronautics,2004,18(S):51-54.
Dynam ic stiffness and vibration reduction efficiency ofmetal rubber
ZHAO Guo-wei,LIDe-yong,CHEN-yong
(School of Astronautics,Beihang University,Beijing 100191,China)
Based on the principle of compressive deformation of cylindricalhelical spring,the dynamic equations of a metal rubber vibration isolation system were derived.The dynamic stiffness,frequency response and vibration characteristics ofmetal rubber were analyzed under the condition of simple harmonic excitation.According to the method of harmonic balance,the influence of excitation frequency on themetal rubber compressionmagnitude,and the influences of compression magnitude and excitation frequency on the metal rubber dynamic stiffness were analyzed.On the basis of the analysis of the metal rubber vibration isolation system,the effects of metal rubber height,cross-sectional area of working surface and excitation frequency on the shock isolation coefficientwere studied.The shock isolation coefficient can provide a reference to the design ofmetal rubber and its applications in engineering.
metal rubber;dynamic model;dynamic stiffness;frequency response;shock isolation coefficient
O328;TB535
:A
10.13465/j.cnki.jvs.2014.22.035
2013-07-02 修改稿收到日期:2013-11-28
赵国伟男,博士,副教授,1976年生
