冲击荷载下单层球面网壳动力响应分析与试验研究

吴 长，王秀丽，马肖彤，梁亚雄

（1．兰州理工大学土木工程学院，兰州 730050；2．兰州理工大学西部土木工程防灾减灾教育部工程研究中心，兰州 730050）

式中：σ0为常应变率处屈服应力；ε·′为有效应变率；C，P为应变率参数，低碳钢取40，5；fh（εpeff）为基于有效塑性应变的硬化函数。其它材料参数见表1。冲击物据冲击荷载相似关系以不同质量的钢球模拟。冲击荷载通过冲击物从水平方向撞击网壳支承柱形式施加。冲击物与钢管柱接触类型选点面接触（NTS）。

冲击荷载下单层球面网壳动力响应分析与试验研究

吴 长1，2，王秀丽1，2，马肖彤1，2，梁亚雄1，2

（1．兰州理工大学土木工程学院，兰州 730050；2．兰州理工大学西部土木工程防灾减灾教育部工程研究中心，兰州 730050）

为分析带下部支承结构的Kiewitt－6型单层球面网壳在冲击荷载下动力响应，在ANSYS／LS－DYNA中建立钢管柱支承的单层球面网壳数值分析模型，据冲击响应特点，总结四种响应模式，研究冲击能量、冲击位置、环梁刚度对上部网壳动力响应影响。进行钢管柱支承的单层球壳模型冲击试验，测量、分析结构的动应力、动位移及加速度，研究冲击柱破坏模式。结果表明，四种响应模式以冲击柱破坏模式（轻微损伤、局部凹陷、压弯破坏、剪切破坏）为典型特征；除响应模式4，网壳动力响应随冲击能量增大而增大；柱中为最不利冲击位置；环梁刚度增大，网壳动力响应减小；有限元分析结果与实测结果吻合较好，验证数值计算方法的正确性。

冲击；单层球面网壳；下部支承结构；动力响应；试验研究

受人为因素影响，世界各地多次发生大型建筑被破坏甚至倒塌事件。“911”后严重性尤其突出。大跨度空间网壳结构以自重轻、刚度大、造型丰富优美被广泛应用。其空间体量大、覆盖范围广常在赈灾中起减少生命财产损失的重要作用，因而在遭遇冲击荷载作用时会出现严重破坏甚至倒塌，造成人员伤亡及财产损失，但针对该类结构受冲击荷载作用研究尚处于起步阶段。李海旺等［1－3］率先对网壳结构在冲击荷载下的动力响应进行研究。范峰等［4－12］分别对网壳在冲击荷载作用下的动力响应、失效模式及失效机理进行研究。王多智等［13－15］认为网壳自重在研究冲击问题时不可忽略，并通过考察网壳杆件受力与破坏形式，建立网壳杆件破坏形式与网壳失效模式间对应关系，对网壳结构冲击响应分析方法及抗冲击特性进行研究。

目前，有关网壳结构受冲击荷载研究均针对落地网壳结构，但实际工程中网壳结构均带下部支承，该支承结构一旦破坏，对上部网壳会产生较大影响。本文通过建立钢管柱支承的Kiewitt－6型单层球面网壳数值模型，分析冲击荷载下整体结构动力响应，归纳总结四种响应模式，研究冲击能量、冲击位置、环梁刚度对上部网壳动力响应影响，并对钢管柱支承的单层球面网壳结构模型进行冲击试验，验证结构抗冲击荷载数值模型。

1 钢管柱支承的单层球面网壳结构冲击响应模式分析

1.1 冲击响应分析数值模型

用计算冲击荷载的有限元显式动力分析软件ANSYS／LS-DYNA建立钢管柱支承的Kiewitt－6型单层球面网壳试验数值模型，见图1。网壳跨度3 m，矢高0．667 m。共240根杆件（圆钢管），92个节点（焊接球节点）。其中主肋杆、环杆截面较大用D22×4，斜杆截面较小用D14×2，焊接球节点规格D80。支承柱用D89×4圆钢管高1．5m。环梁用截面150mm×100 mm×5 mm方钢管。网壳杆件、支承柱单元采用3节点梁单元Beam161，屋面荷载通过质量单元Mass166施加，冲击物采用8节点六面体实体单元Solid164，材料模型用RigidBody刚性体模型。

钢材料模型用分段线性塑性（Piecewise Linear Plasticity）模型，该模型考虑应变率效应影响。应变率与屈服应力关系为

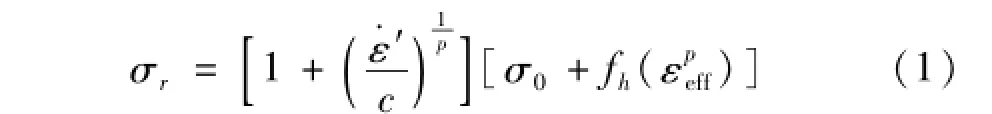
式中：σ0为常应变率处屈服应力；ε·′为有效应变率；C，P为应变率参数，低碳钢取40，5；fh（εpeff）为基于有效塑性应变的硬化函数。其它材料参数见表1。冲击物据冲击荷载相似关系以不同质量的钢球模拟。冲击荷载通过冲击物从水平方向撞击网壳支承柱形式施加。冲击物与钢管柱接触类型选点面接触（NTS）。

图1 分析模型Fig．1 Analysismodel

表1 下部柱及上部杆件材料模型Tab.1 Materialmodel of suppor ting column and member

1.2 冲击响应模式及动力响应分析

据冲击物在现实中的变化，以单一变量形式对计算模型进行参数分析，冲击荷载分析方案见表2。表中ν为冲击物速度；D为钢球直径；m为不同直径钢球质量；h为冲击点距柱底距离。

表2 参数分析方案Tab.2 Parameters of analysis

据参数分析结果，据动力响应特点，将冲击荷载下钢管柱支承的单层球面网壳响应模式分为4类：①支承柱冲击点处有较小损伤，整体结构处于弹性阶段，网壳位移响应较小；②柱冲击区域进入塑性，冲击点塑性应变达失效应变，冲击柱局部凹陷，网壳位移响应增大，靠近冲击区域个别杆件应力增大；③冲击柱塑性区域扩展，弯曲变形明显，冲击柱压弯破坏，上部网壳位移响应较大，近冲击区域个别杆件进入塑性；④冲击柱受高速冲击剪切破坏，网壳位移响应较小。对冲击位置柱中h＝800 mm处以不同质量、速度进行参数分析，各响应模式变形见图2～图5。

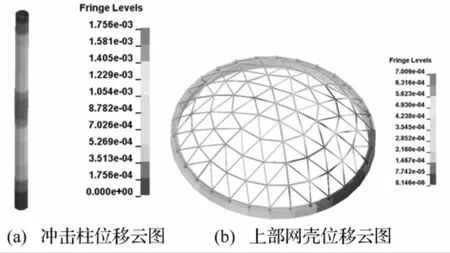
图2 节点位移云图（模式1：m＝4．1 kg，ν＝10 m／s）Fig．2 Nephogram of node displacement

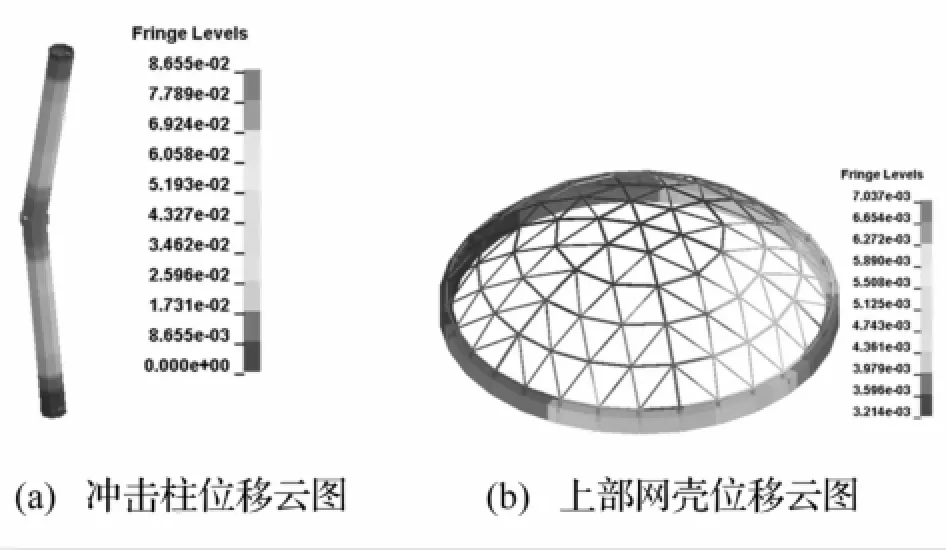
图3 节点位移云图（模式2：m＝32．9 kg，ν＝15 m／s）Fig．3 Nephogram of node disp lacement

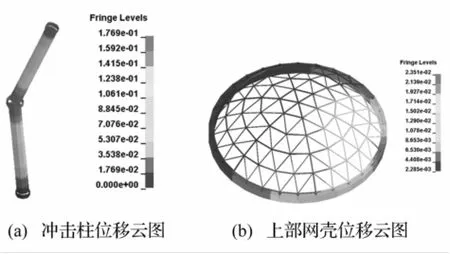
图4 节点位移云图（模式3：m＝123．3 kg，ν＝10 m／s）Fig．4 Nephogram of node displacement

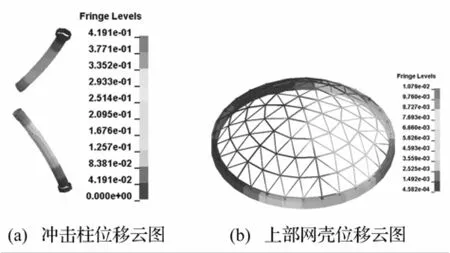
图5 节点位移云图（模式4：m＝161．5 kg，ν＝50m／s）Fig．5 Nephogram of node displacement

四种响应模式的冲击力时程曲线见图6。由图6看出，模式1、2、3冲击力为三角形脉冲荷载。模式4冲击力时程出现两次峰值，此因冲击柱发生冲切破坏，冲击物穿过冲击柱与相对柱发生二次撞击。一次撞击的四种模式冲击力作用时间分别为0．013 s、0．036 s、0．984 s、0．018 s，冲击力峰值模式1、2、4随冲击能量增大而增大，但模式3的冲击持时明显大于其它模式，表明支承柱变形较大，由于冲击物与支承柱接触时间长，致使能量有较长时间由冲击区域传至上部网壳。模式4中因第一次撞击耗散能量较小，撞击后冲击物仍有较大动能，二次撞击能量大于一次撞击能量，持时较短，故冲击力峰值大于第一次冲击力峰值。

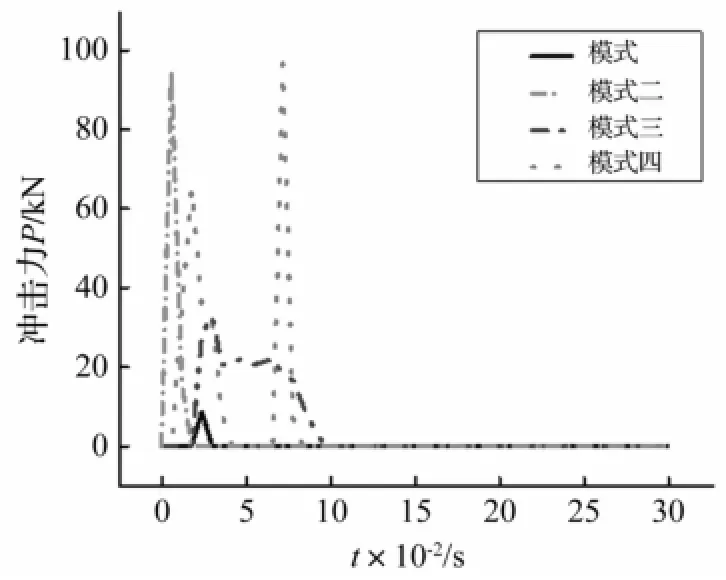
图6 冲击力时程曲线Fig．6 Time-history curvses of impact

图7为各响应模式下支承柱及网壳应力峰值。由图7看出，随冲击能量增大上下部结构应力峰值均增大，当冲击柱发生剪切破坏时应力峰值有所减小。除模式1外，应力均远大于结构的屈服应力，说明在受冲击区域内结构进入塑性状态，由于应力波传播效应，下部柱应力均大于上部网壳应力。网壳结构以最外环近冲击区域斜杆应力最大。

1.3 冲击能量分析

冲击能量为冲击物所具有的初动能，可由初始冲击质量与速度求出。撞击中因冲击物与支承柱接触致冲击物动能迅速减小并转化为网壳整体结构总能量，该总能量即为冲击结束时所得能量，由三部分组成，即下部支承柱所得能量、环梁所得能量及上部网壳所得能量。

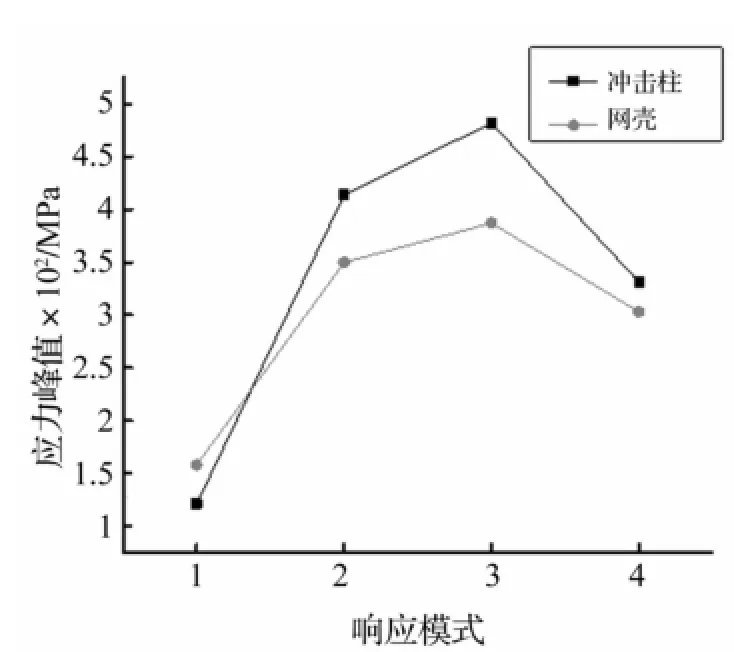
图7 各响应模式下杆件应力峰值Fig．7 Peak stress ofmember on each responsemodel

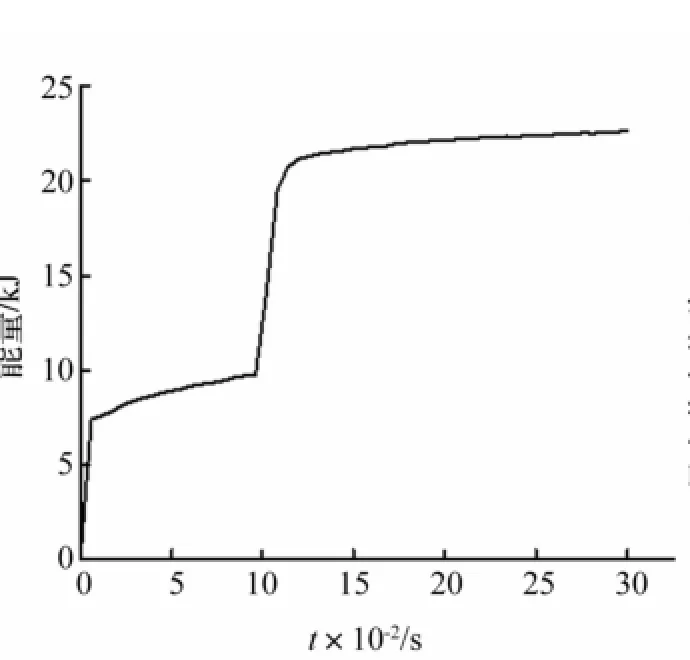
图8 冲击柱的能量时程曲线Fig．8 Energy time-history curve of impact column

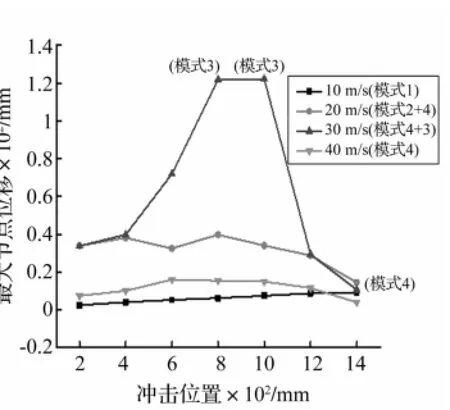
图9 冲击位置对网壳最大节点位移影响Fig．9 Influence of the impact location on the Maximum node displacement

取质量32．9 kg、冲击位置柱中、以速度为参数进行分析，对应的冲击能量及主要动力响应见表3。速度在10～30 m／s时冲击物撞击后反弹，冲击物与支承柱发生一次撞击；速度在40～60 m／s时冲击物与冲击柱相对支承柱发生二次撞击，表中数据对应第一次撞击后能量。本文重点考虑一次冲击，二次冲击不做详细分析。由表3看出，速度在10～30 m／s时网壳整体结构所得能量约占初始冲击能量的95%，剩余能量为冲击物动能。冲击柱变形耗散大部分能量，其次为环梁，网壳所得能量最小，小于总能量的5%。由于冲击能量增加冲击柱变形增大，冲击持时增加，使环梁及网壳获得较多能量，位移响应增大。响应为模式3时环梁及上部网壳获得能量最大，位移响应最大，网壳最大节点位移达115．6 mm，环梁变形明显。40～60 m／s时由于冲击速度极快，冲击持时较短，整体结构响应模式为模式4，冲击能量由冲击柱的剪切破坏耗散。第一次冲击网壳整体结构获得冲击能量低于30%，且随速度增加占比减小。第一次冲击后大部分冲击能量被冲击物带走。上部网壳位移响应较小，且随速度增加环梁、网壳响应逐渐较小。随后冲击物与相对柱发生撞击，相对柱破坏较大，并耗散大量能量，见图8（ν＝40 m／s）。第二冲击柱响应模式随冲击速度增加依次呈现响应模式1～4特点，且上部网壳响应较大区域由近第一次冲击区域转向近第二次冲击区域逐渐较小。此过程较复杂，本文重点考虑一次冲击，二次冲击不做详细分析。

总体上，冲击力峰值随冲击能量增加而增加，但增加幅度不大。

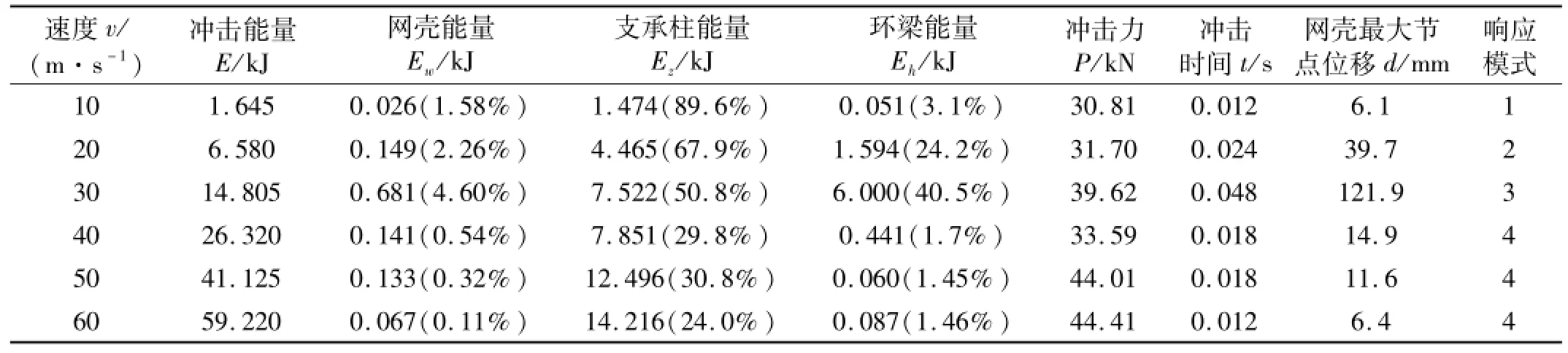
表3 冲击能量及主要动力响应结果对比Tab.3 Com parison of energy and major dynam ic response results

1.4 不同冲击位置动力响应分析

取冲击质量32．9 kg，速度10 m／s、20 m／s、30 m／s、40 m／s，以冲击位置为参数进行分析。不同冲击位置上部网壳响应模式与最大节点位移比较见图9。由图9看出，速度为10 m／s时由于冲击能量小，网壳响应模式为模式1；冲击位置为柱顶时网壳节点位移最大，柱底最小（同试验结果），此因碰撞后钢柱变形极小，应力波迅速向非冲击区传播，且不断衰减，故离冲击区域越近动力响应越大。速度取20 m／s时，除冲击柱顶外各算例对应的网壳最大节点位移在28．7～39．7 mm之间相差不大。此因冲击点离柱两侧约束位置不同、柱的变形不同、冲击过程持时不同，故传至上部网壳的能量略有差异，且各算例对应的响应模式均为模式2。冲击柱中时网壳节点位移最大（39．7 mm）。冲击柱顶时因其为与环梁连接部位，刚度相差较大，冲击瞬间冲击力峰值较大，柱顶被冲断，网壳最大节点位移仅14．41 mm。速度取30 m／s冲击位置为柱底与柱顶位置时（h＝200 mm、400 mm、1 200 mm、1 400 mm）与20 m／s相比，虽冲击能量增加2．25倍，但网壳最大节点位移基本相同，因此时冲击柱遭剪切破坏，上部网壳所得能量未增加。冲击柱中区域时（h＝600 mm、800 mm、1 000 mm），其响应模式为3，由于柱中离支座较远，所受约束较小，位移较大，冲击过程持时较长，上部网壳获得能量较多。速度取40m／s时网壳结构对应的响应为模式4，上部网壳节点位移较小，冲击柱中时网壳节点位移最大，柱顶最小，此因柱顶约束最弱，冲击持时最短。

总之，柱顶较易被冲断，柱中变形最大，当响应模式为①时，柱顶为最不利冲击位置；其它响应模式中柱中区域为最不利冲击位置。

1.5 不同环梁刚度动力响应分析

因冲击应力波由冲击点开始，通过环梁传递到上部网壳，故环梁刚度对上部网壳的动力响应亦有影响。取冲击物质量32．9 kg，冲击物速度20 m／s，冲击物位置柱中（h＝800 mm），改变环梁截面进行分析。各部能量及上部网壳最大节点位移见表4。由表4看出，随环梁刚度增加，网壳所得能量及最大节点位移逐渐递减。环梁刚度越小吸收能量越小，传递到上部网壳的能量越大。环梁刚度会影响各部能量分配，随环梁刚度增大环梁耗散能量先增大后减小，支承柱耗散能量先减小后增大。

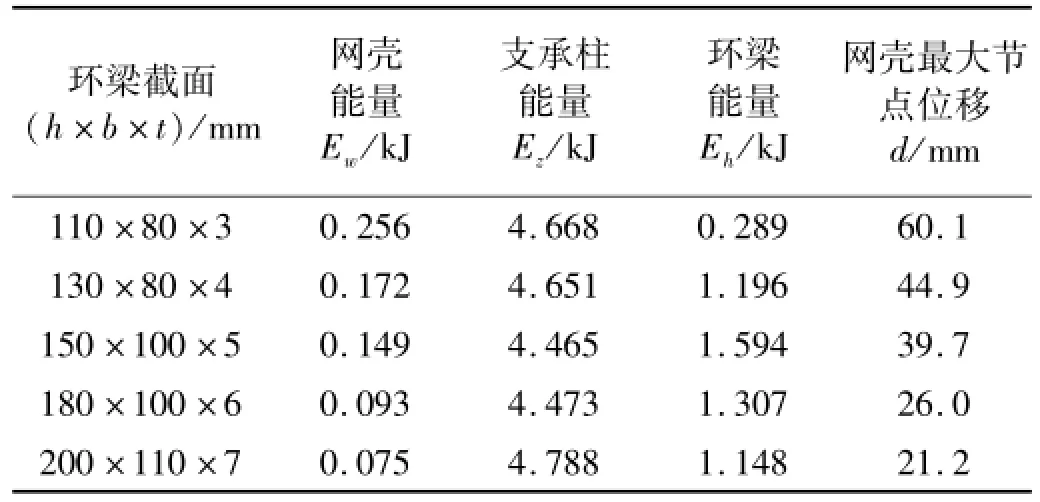
表4 冲击能量及位移响应结果对比Tab.4 Comparison of energy and disp lacement response results

2 试验研究

2.1 试验目的

（1）现场观测带下部支承结构的单层球面网壳受冲击力作用的破坏形态及历程，采集结构的动态位移、应变、加速度，分析动力响应，验证该结构的数值模型及动力响应模式。

（2）分析钢管柱支承的单层球面网壳结构受冲击荷载作用时下部柱的破坏形态及上部网壳结构的动力响应。

2.2 试验模型

K6型单层球面网壳模型平面示意图见图10，试验模型见图11。

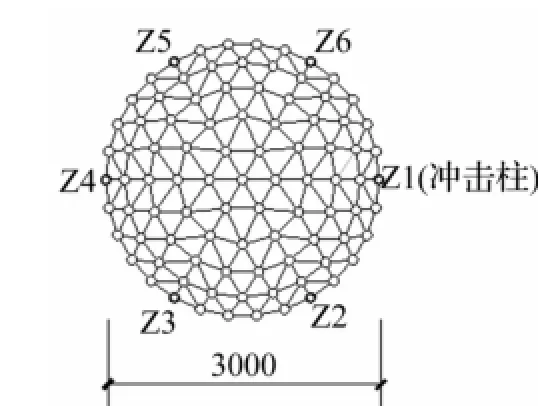
图10 模型平面示意图Fig．10 Plane sketch ofmodal

图11 试验模型Fig．11 Modal test

2.3 试验装置

试验在自行设计的冲击模拟加载装置上进行，利用冲击物由高处滚落时的冲力作为集中冲击力施加。加载架见图12（a），高度5．8 m，上部平台尺寸3 m× 3．3 m，坡道长5．7 m，坡度42°。加载架通过轨道（图12（b））及调高装置（图12（c））模拟不同加载工况，冲击出口可调节为400 mm，600 mm，800 mm，1 000 mm，1 200 mm，1 300 mm。加载架可承载最大冲击物质量为10 t。

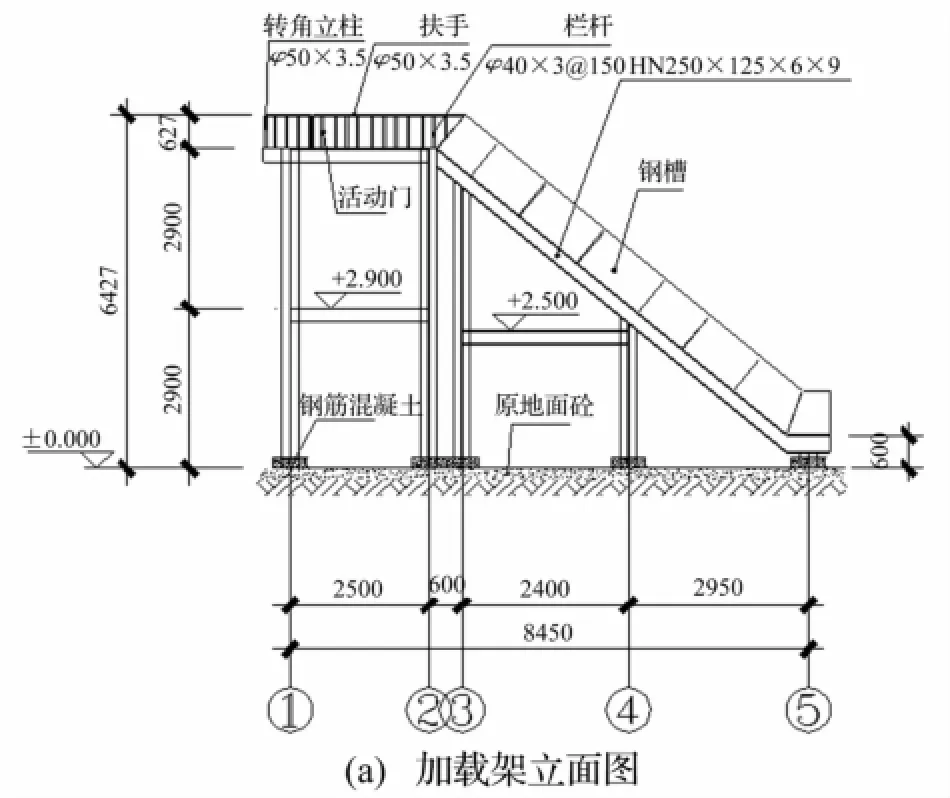
图12 冲击试验加载架Fig．12 Impact loading frame of test

2.4 试验工况

试验时通过改变冲击物质量及下落高度模拟不同冲击荷载。冲击试验加载点选支承柱上高度为400 mm、600 mm、800 mm三处。加载后间隔30 min再进行下个工况。试验工况按钢球释放高度相同、撞击点不同及初始总冲击能量相同、撞击点不同原则确定，共分20个工况，见表5。

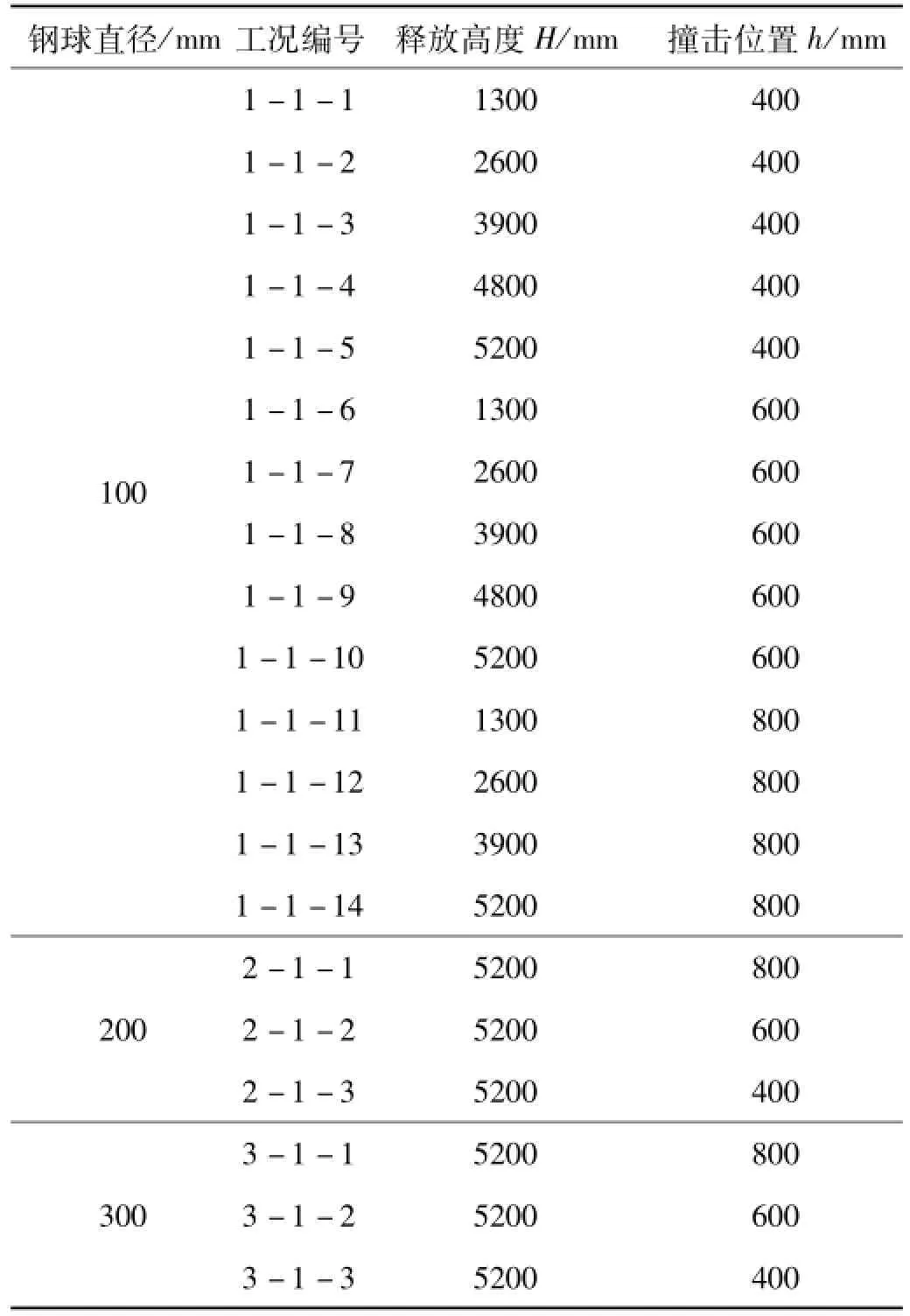
表5 试验工况Tab.5 Test cond itions

2.5 数据采集与测点布置

据试验目的及模型对称特点共布置5个加速度测点（加速度传感器型号DH151，量程30 000 g），即冲击柱Z1、相邻柱Z2、相对柱Z4顶部各1个、冲击柱相邻网壳最外环主肋节点1个及网壳顶点1个。4个位移测点分别为：与冲击柱相邻网壳最外环主肋节点D1、冲击柱Z1顶部D2、中部D5、相邻柱Z2顶部D4、相对柱Z4顶部D3。8个应变测点见图13。冲击柱Z1的6个应变测点为：柱底、1／5柱高、1／3柱高、1／2柱高、2／3柱高、柱顶，编号Y9～Y14。相邻柱Z2的3个应变测点位置为：柱底、1／5柱高、1／3柱高，编号Y15～Y17。相对柱Z4的3个应变测点为：柱底、1／5柱高、1／3柱高，编号为Y18、Y19。

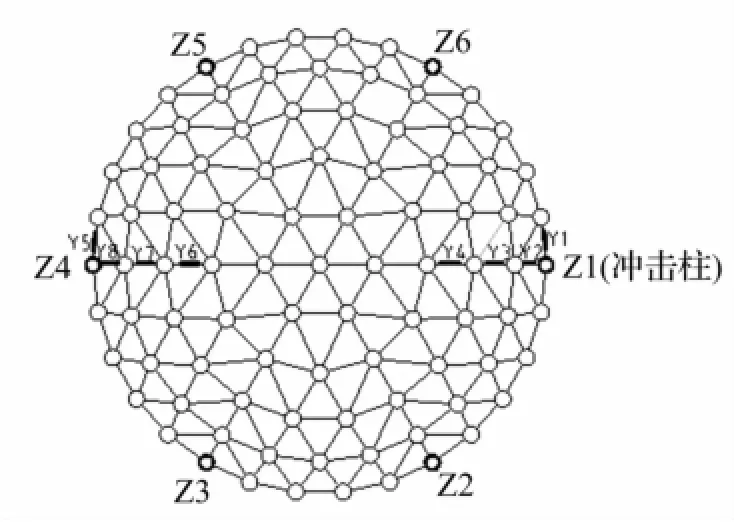
图13 上部网壳应变片布置图Fig．13 Strain gauge position of the upper reticulated shell

3 试验现象

钢球直径为100 mm时小球沿轨道以不同速度及略有差异入射角冲击下部柱，碰撞瞬间有较大声音，钢球反弹后落地。因钢球质量较小冲击载荷亦小，冲击效果仅产生下部柱的刚体平动及绕柱顶转动，柱略有倾斜，见图14（a），上部网壳结构几乎未振动。钢球直径为200 mm时，随冲击荷载增加碰撞瞬间冲击柱振动明显，上部网壳结构亦有振动，冲击柱碰撞部位有局部凹陷，见图14（b）。钢球直径为300 mm时冲击柱出现较明显弯曲变形，见图14（c），与环梁连接的焊缝发生破坏，上部网壳振动明显。

图14 冲击柱的变形形态Fig．14 Deformation patterns of column

4 试验结果分析

试验条件所限，加载架能实现的最大冲击速度为10 m／s，故试验验证的仅为数值分析中冲击物速度ν≤10 m／s的特例。

4.1 动力响应分析

冲击位置为柱下部时（h＝400 mm），不同工况冲击柱Z1测点Y9～Y14的应力峰值见表6。由表6看出，工况为1－1－1～1－1－5时，由于冲击能量小冲击柱应力均较小，结构处于弹性状态，故分析均采用钢球从平台处滚下工况（1－1－5、1－1－10、1－1－14、2－1－1、2－1－2、2－1－3），对应冲击速度为10 m／s。工况2－1－3时因钢柱整体弯曲变形，柱中拉应力较大，柱底压应力较大。

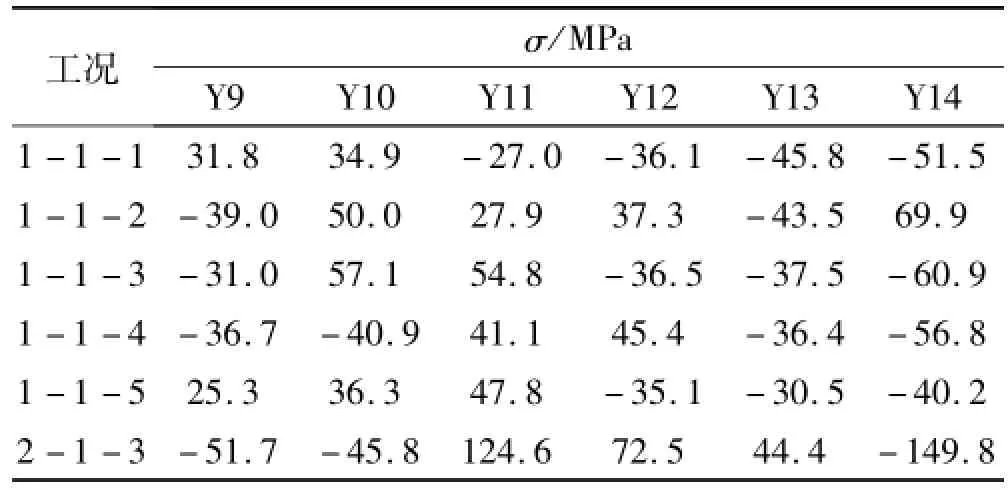
表6 冲击柱测点Y9～Y14应力峰值Tab.6 Stress extremum of Y9～Y14

冲击高度为600 mm时，1－1－10、2－1－2、3－1－2工况部分测点应力峰值见表7。由表7看出，杆件应力试验与数值结果误差在3%～11%之间，表明带下部支承柱的网壳结构数值模型正确。工况3－1－2个别数据误差较大，因冲击柱已多次受冲击物撞击，数值模型未考虑损伤累积影响，而冲击柱略有倾斜，故数值分析模型与试验模型存在差异。

表7中Y1、Y5为环杆测点，Y2、Y4、Y6、Y8为主肋测点，环杆及主肋应力变化不大，说明冲击为局部性强荷载，在冲击作用下通常与冲击物直接接触的冲击区承受大部分冲击能量，少部分冲击能量通过环梁传到网壳。Y10（h＝300 mm）、Y11（h＝500 mm）、Y14（柱顶）为冲击柱应变测点，测点Y11离冲击点最近应力峰值最大，且随冲击能量增大而增大。冲击质量为123．3 kg时柱中点应力瞬间增加到490．3 MPa，表明该点材料已屈服，此时应力大于材料普通屈服应力207 MPa，此因应变率效应影响。网壳对应响应模式为模式3，与数值分析结构吻合较好。Y15、Y16、Y17为相邻柱（Z2）测点，应力峰值明显小于冲击柱应力峰值；Y18、Y20为相对柱（Z4）测点，应力峰值明显小于相邻柱应力峰值，表明冲击能量由冲击区传递至非冲击区并逐渐衰减，使不同位置支承柱受力差距较大。

冲击柱测点Y11采集的应力时程曲线见图15。由图15看出，撞击高度600 mm时不同冲击物质量下应力峰值分别为53．1 MPa、110．5 MPa、490．3 MPa，表明冲击点区域应力随冲击能量增加而增加，且变化较大。冲击能量较小时（图15（a）、（b）），冲击过程结束后测点应力明显减小；冲击结束后（图15（c））杆件应力一直在320 MPa附近，表明冲击区域已产生永久塑性变形。由冲击位置800 mm时Y11应变测点应力时程（图15（d））看出，应力峰值瞬间增加到510 MPa，大于490．3 MPa（h＝600 mm），此因冲击位置不同结构响应也不同，冲击高度越高支承柱约束越弱，变形越大。

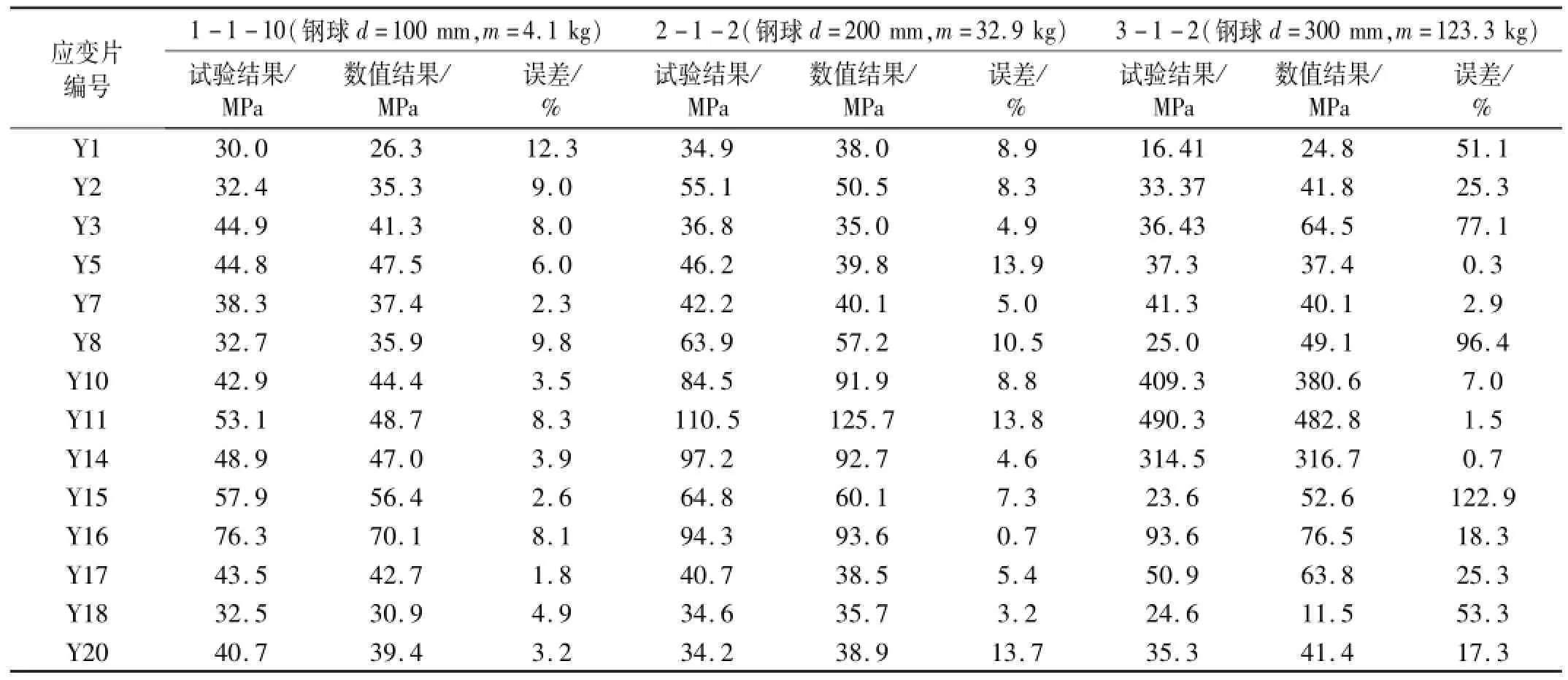
表7 部分测点应力峰值Tab.7 Stress extremum of partmeasuring point

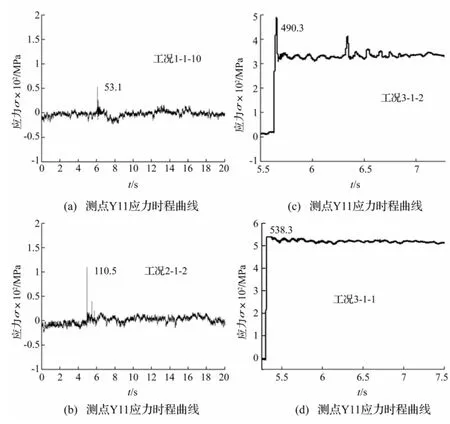
图15 不同工况测点Y11应力时程曲线Fig．15 Stress time-history curve of Y11 on different test conditions

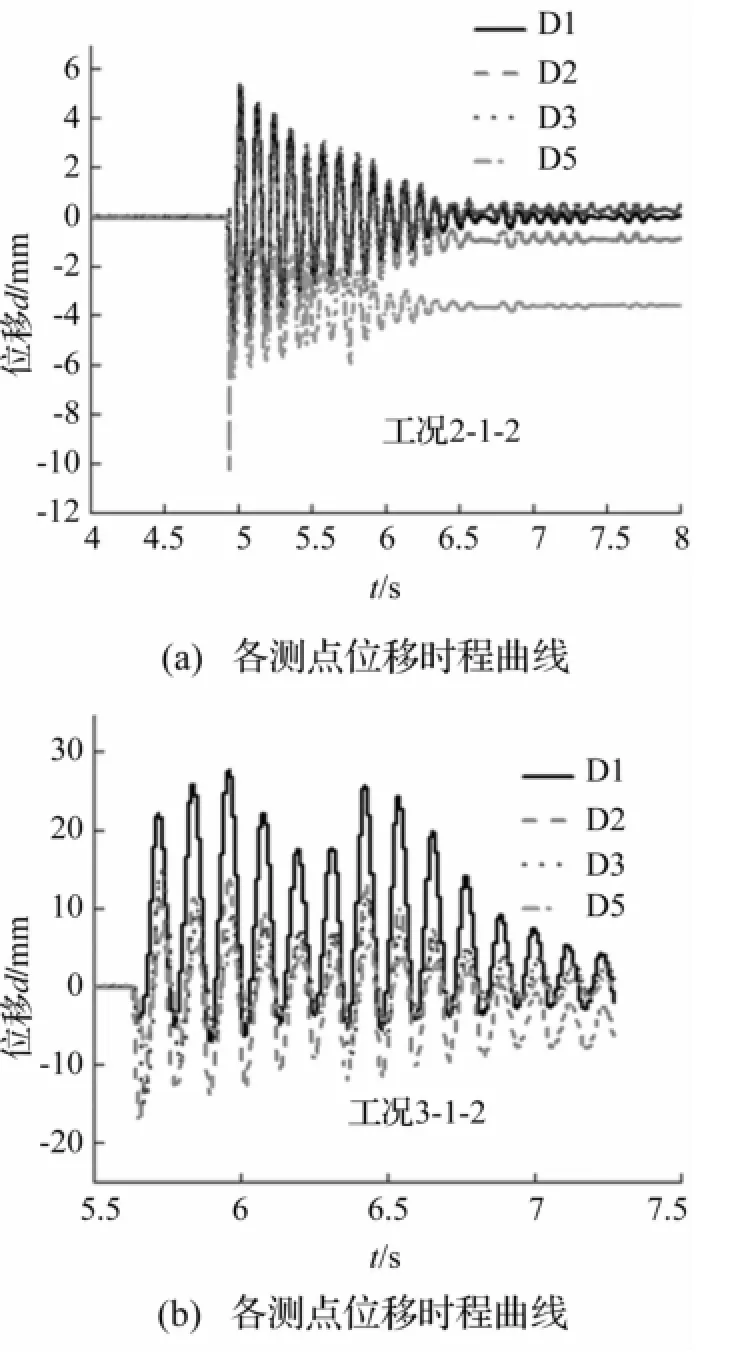
图16 位移时程对比Fig．16 Contrast of displacement time histories

测点D1～D5采集的水平位移时程曲线见图16。由图16看出，冲击瞬间各测点位移基本达到峰值，冲击柱测点D5位移峰值较大，而网壳测点D1位移峰值较小，由于应力波传播需一定时间，网壳距冲击点有一定距离，故冲击瞬间位移幅值较小。在10 ms以内网壳及其它测点位移峰值迅速增大。冲击能量较小时（图16（a）），随冲击过程结束位移逐渐减小，最后在阻尼作用下整体结构停止振动。冲击能量较大时（图16（b））网壳位移峰值明显增大，且未立即呈衰减规律，在随后振动中衰减速率较小，表明网壳振动较明显，持续时间较长。数值分析与试验实测结果误差率在3%－10%之间。

工况2－1－2上部网壳顶点竖向加速度（A1）与冲击柱Z1柱顶加速度（A2）时程对比见图17。由图17看出，支承柱振动不仅引起上部网壳的水平振动，亦引起竖向振动，最大峰值为561．37 m／s2，冲击柱测点A2加速度峰值为1495 m／s2。可见，几个柱顶加速度峰值相差不大，几乎同时在冲击瞬间达到峰值。随冲击能量增大上部网壳加速度峰值有增大趋势但变化不大，而下部支承柱加速度峰值反而减小；工况3－1－2中冲击柱Z1测点A2加速度峰值为1 002 m／s2，减小33%，此因下部柱损伤较大，变形较大所致。

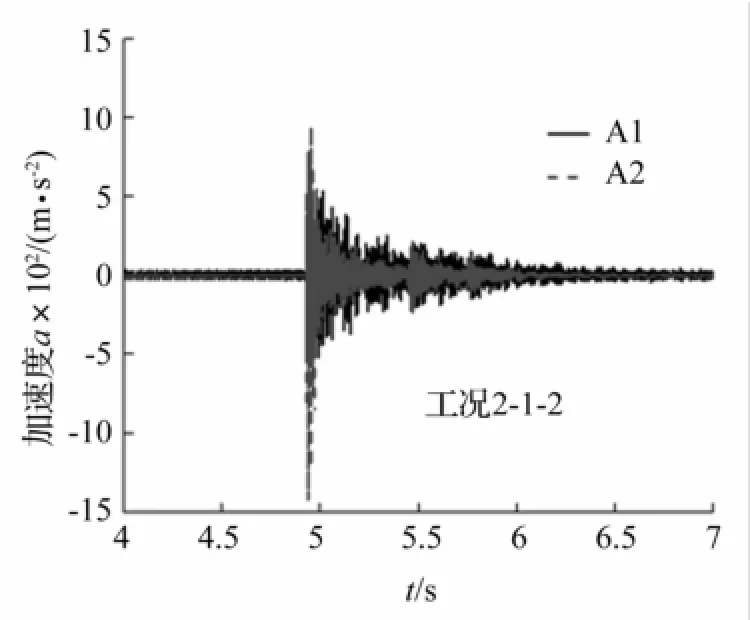
图17 加速度时程对比Fig．17 Contrastof acceleration time histories

4.2 冲击柱破坏模式分析

支承柱耗散的能量主要集中于冲击柱（比例95%），而冲击柱破坏位置主要集中于冲击区域。冲击荷载较小时冲击柱在冲击点有轻微损伤仍处于弹性阶段，见图18（a）。冲击荷载增加时局部损伤范围扩大，冲击柱出现局部凹陷，其受力状态主要以剪切为主（图14（b））。随冲击荷载增加该柱剪切状态未破坏进入弯曲状态，在上部竖向荷载共同作用下发生压弯破坏，见图18（b）。可见，冲击柱的破坏形式即能体现冲击荷载大小，亦能反映其破坏时传递给上部网壳能量多少。而外传能量的多少为决定网壳动力响应大小的主要因素。试验条件所限，未能验证高速冲击的冲击柱剪切破坏模式。

图18 冲击柱破坏形态Fig．18 Damage patterns of column

5 结 论

（1）据钢管柱支承的单层网壳结构冲击响应特点分四种模式，而柱的破坏模式有轻微损伤、局部凹陷、压弯破坏及剪切破坏。对应的上部网壳位移响应先增大后减小；近冲击区域斜杆应力较大。

（2）冲击能量主要由冲击柱变形耗散。支承柱获得能量最多，其次为环梁，网壳获得能量最少。响应模式不同支承柱、环梁、网壳获得能量比例亦不同。支承柱破坏模式对网壳动力响应影响最大。

（3）对上部网壳动力响应，冲击能量较小时柱顶为最不利冲击位置；冲击能量增加时柱中为最不利冲击位置；冲击能量相同时冲击位置不同引起的响应模式亦不同，柱顶最易冲断。

（4）增加环梁刚度，网壳所得能量及位移响应逐渐减小。响应模式3时环梁刚度对网壳响应影响最大。

（5）利用冲击试验对冲击速度10 m／s的数值分析结果及冲击柱以轻微损伤、局部凹陷，压弯破坏为典型特征的响应模式进行验证。

［1］李海旺，郭可，魏剑伟，等．撞击载荷作用下单层球面网壳动力响应模型实验研究［J］．爆炸与冲击，2006，26（1）：39－45．

LI Hai-wang，GUO Ke，WEI Jian-wei，et al．The dynamic response of a single-layer reticulated shell to drop hammer impact［J］．Explosion and Shock Waves，2006，26（1）：39－45．

［2］郭可．单层球面网壳在冲击载荷作用下的动力响应分析［D］．太原：太原理工大学，2004．

［3］史俊亮．K8型单层网壳在撞击荷载作用下的动力响应研究［D］．太原：太原理工大学，2005．

［4］王多智．冲击荷载下网壳结构的失效机理研究［D］．哈尔滨：哈尔滨工业大学，2010．

［5］谭双林．单层球面网壳在冲击荷载下的动力响应与失效模式研究［D］．哈尔滨：哈尔滨工业大学，2009．

［6］田永红．冲击荷载下短程线型和肋环斜杆型球面网壳的失效模式［D］．哈尔滨：哈尔滨工业大学，2010．

［7］范峰，王多智，支旭东，等．K8型单层球面网壳抗冲击荷载性能研究［J］．工程力学，2009，26（6）：75－81．

FAN Feng，WANG Duo-zhi，ZHI Xu-dong，et al．Performance for Kiewitt8 single-layer reticulated domes subjected to impact load［J］．Engineering Mechanics，2009，26（6）：75－81．

［8］王多智，支旭东，范峰，等．冲击荷载下K8单层球面网壳的破坏类型［J］．工程力学，2008，25（S2）：144－149．

WANG Duo-zhi，ZHI Xu-dong，FAN Feng，et al．Failure patterns of Kiewitt8 single-layer reticulated domes under impact loads［J］．Engineering Mechanics，2008，25（S）：144－149．

［9］范峰，王多智，支旭东，等．冲击荷载下凯威特型球面网壳的失效模式及其判别方法［J］．土木工程学报，2010，43（5）：56－62．

FAN Feng，WANG Duo-zhi，ZHI Xu-dong，et al．Failure modes and discrimination method for Kiewitt reticulated dome under impact loads［J］．China Civil Engineering Journal，2010，43（5）：56－62．

［10］Fan Feng，Wang Duo-zhi，Zhi Xu-dong，et al．Failure modes for single-layer reticulated domes under impact loads［J］．Transactions of Tianjin University，2008，14（S1）：545－550．

［11］王多智，范峰，支旭东，等．冲击荷载下单层球面网壳的失效机理［J］．爆炸与冲击，2010，30（2）：169－177．

WANG Duo-zhi，FAN Feng，ZHI Xu-dong，et al．Failure mechanism of single-layer reticulated domes subjected to impact loads［J］．Explosion and Shock Waves，2010，30（2）：169－177．

［12］Wang Duo-zhi，Zhi Xu-dong，Fan Fen，et al．Failure process and energy transmission for single-layer reticulated domes under impact loads［J］．Transactions of Tianjin University，2008，14（S1）：551－557．

［13］王多智，范峰，支旭东，等．考虑重力效应的单层球面网壳抗冲击荷载性能［J］．哈尔滨工业大学学报，2009，41（8）：19－23．

WANG Duo-zhi，ZHI Xu-dong，FAN Feng，et al．Performance for single-layer reticulated domes under impact load and gravity［J］．Journal of Harbin Institute of Technology，2009，41（8）：19－23．

［14］王多智，范峰，支旭东，等．基于杆件破坏形式的冲击荷载下单层球面网壳失效机理分析［J］．振动与冲击，2009，28（10）：54－59．

WANG Duo-zhi，FAN Feng，ZHI Xu-dong，et al．Failure mechanism for a single-layer reticulated dome under impact loads based on energy transfer［J］．Vibration and Shock，2009，28（10）：54－59．

［15］王多智，范峰，支旭东，等．网壳结构冲击响应分析方法及抗冲击特性研究［J］．振动与冲击，2013，32（10）：111－117．

WANG Duo-zhi，FAN Feng，ZHI Xu-dong，et al．Dynamic response analysis and anti-shock performance of reticulated shell under impact［J］．Journal of Vibration and Shock，2013，32（10）：111－117．

Numerical analysis and experimental study on the dynam ic response of single-layer reticulated shell under im pact

WU Chang1，2，WANG Xiu-li1，2，MA Xiao-tong1，2，LIANG Ya-xiong1，2
（1．Lanzhou University of Technology，School of Civil Engineering，Lanzhou 730050，China；2．Western Center of Disaster Mitigation in Civil Engineering of Ministry of Education，Lanzhou University of Tech，Lanzhou 730050，China）

In order to analyze the dynamic response mode of Kiewitt-6 single-layer reticulated shell with substructure under impact，a model of shell with steel pipe column for numerical analysis was established by using the ANSYS／LS-DYNA program．Four dynamic response modes were put forward according to the features of dynamic responses．The influences of the impactenergy，impact location，and stiffnessof ring beamswere studied．The impact test on the single-layer reticulated shell model with steel pipe columns was conducted．The dynamic stress，dynamic displacement and acceleration weremeasured and analyzed，and the damage patterns of impacted columnswere studied．The results show that response modes are typically characterized by the damage patterns of impacted columns（slight damage，local dent，press-bend failure and shear failure）．The dynamic response of the reticulated shell increaseswith the increase of impact energy with the exception of the response mode 4．Themost unfavorable impact position is the central part of columns．The dynamic response of reticulated shell decreases with the increase of stiffness of ring beams．The numericalmodel was also proved to be reasonable by comparing the theoretical and experimental results．

impact；single-layer reticulated shell；substructure；dynamic response；experimental study

TU393．3 TU317．1

：A

10．13465／j．cnki．jvs．2014．22．016

国家自然科学基金面上项目（51278236）；国家科技支撑计划（2011BAK12B07）

2014－04－01 修改稿收到日期：2014－05－10

吴长女，博士生，1981年生

王秀丽女，教授，博士生导师，1963年生邮箱：wangxl9104＠163．com