带覆盖层半空间内SH波对浅埋圆孔及夹杂散射与地震动

齐 辉，陈冬妮，蔡立明

（哈尔滨工程大学航天与建筑工程学院，哈尔滨 150001）

带覆盖层半空间内SH波对浅埋圆孔及夹杂散射与地震动

齐 辉，陈冬妮，蔡立明

（哈尔滨工程大学航天与建筑工程学院，哈尔滨 150001）

采用大圆弧假定法将具有地表覆盖层的半空间直边界问题转化为曲面边界问题。借助Helmholtz定理预先给出问题波函数的一般形式解，再利用复变函数法及边界条件将问题化为求解波函数未知系数的无穷线性代数方程组，截断该方程组即可求解带地表覆盖层的半空间内浅埋圆孔及夹杂对SH波散射问题，并给出地面运动数值结果。定性分析入射波数、入射角度、埋深、夹杂刚度及覆盖层刚度等对地面运动影响。研究表明，浅埋圆孔及夹杂与地表覆盖层间存在强烈的相互作用，地震动会受较大影响。

地表覆盖层；圆孔；夹杂；SH波散射；大圆弧假定法；地震动

研究SH波作用下局部地形、地质构造对地震动影响对地震工程学及地下结构抗震与抗爆具有重要的理论意义及应用价值。针对凹陷与凸起地形影响地震动研究已有很多［1－4］。本文研究地震波传播过程中接近带覆盖层地表面时SH波对浅埋圆孔及夹杂的散射问题，确定地面运动。若将浅埋多圆孔及夹杂视为“隐蔽地形”，则本文所研究问题可与凹陷、凸起地形研究同归属地形影响范畴。隐蔽地形研究成果见文献［5－8］。

本文利用大圆弧假定法［9］将半空间直边界用一半径较大圆孔边界拟合，使原问题转化为半空间内大圆孔、小圆孔及圆柱形夹杂对SH波散射问题；联合复变函数法及波函数展开法给出具有地表覆盖层的弹性半空间内圆孔与夹杂在稳态SH波作用下地震动问题解。

1 理论分析

1.1 计算模型

计算模型见图1。在地表覆盖层下边界建立总体坐标系XOY，在圆孔与圆柱形夹杂圆心建立局部坐标系XjOjYj。地表覆盖层上边界标记为TU，下边界标记为TD，覆盖层厚度为h2，密度为ρ2，剪切弹性模量为μ2；利用半径较大圆拟合地表直边界，逼近覆盖层大圆弧中心记为O′，至上边界半径记为RU，至下边界半径记为RD；浅埋圆孔及圆柱形夹杂记为TS（S＝1，…，m，cs为第s圆孔或夹杂中心坐标，即第s圆孔或夹杂圆心在总体坐标下的坐标，半径为as；夹杂密度及剪切弹性模量分别为ρj，μj；基体介质密度及剪切弹性模量分别为ρ1，μ1。针对研究问题中存在不同边界条件，将整个区域分割成Ⅰ、Ⅱ、Ⅲ区域进行分析。区域Ⅰ为基体半无限空间，区域Ⅱ为地表覆盖层，区域Ⅲ为圆柱形夹杂，TD为区域Ⅰ、Ⅱ的公共边界。

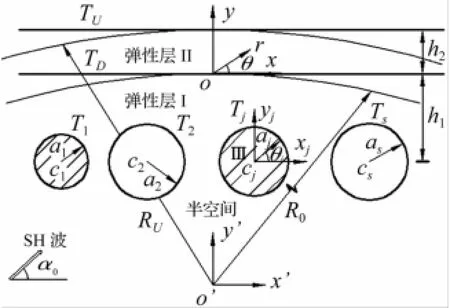
图1 SH波对浅埋多圆形结构散射计算模型Fig．1 Themodel of scattering of shallow circular structures impacted by SH-wave

1.2 控制方程

1.3 基体中散射波求解

1.4 地表覆盖层中散射波求解

式中：z′＝z＋i RD；Cn，Dn（n＝0，±1，±2，…）为待求系数。

应力可表示为

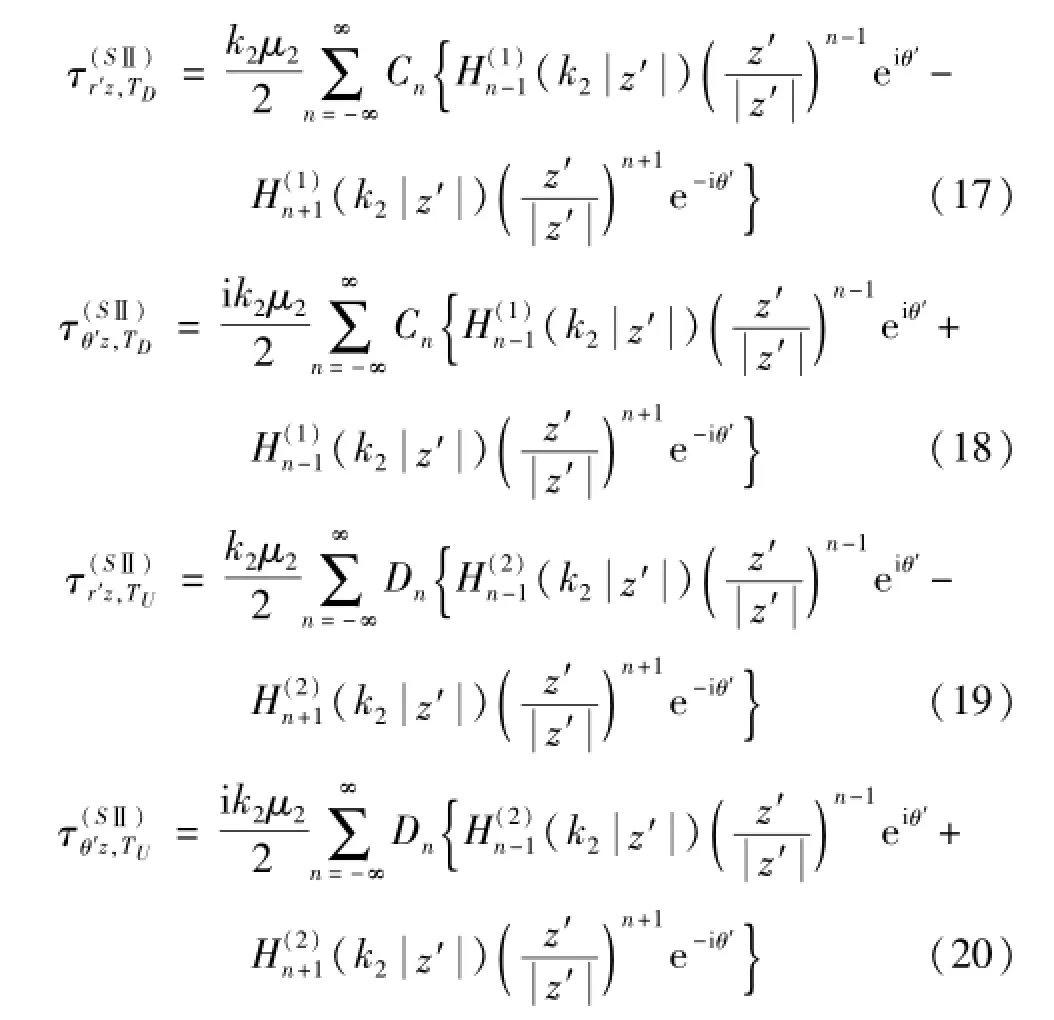
1.5 夹杂驻波求解

1.6 问题解答

将式（27）第一式两边同乘exp（－i mθj），第二、三、四式两边同乘exp（－i mθ′）（m＝0，±1，±2，…），第五、六式两边同乘exp（－i mθ2）（m＝0，±1，±2，…）并在（－π，π）上积分，化简成未知系数A1n，A2nBn，Cn，Dn，En的一组无穷代数方程组。通过精度控制截取方程组有限项求解。经验算，本文计算精度可达10－5。

2 地面运动数值结果

本文模型对SH波散射时地震动影响重要分析内容为地表位移幅值。在地震工程与结构抗震分析中主要关注地表面加速度最大幅值及相位变化。对稳态SH波而言，若求得浅埋结构影响下地表各点位移即可求出各点加速度。在入射SH波作用下，地表水平界面总波场可写为

式中：W（t）为位移幅值；φ为W（t）相位。

对图2具有相同半径（为便于分析，用无量纲参数，取圆孔及夹杂半径R＝1．0），纵向排列圆孔及夹杂对地震动影响进行分析。参数组合设为μ*1＝μ2／μ1，μ*2＝μ3／μ1，k*1＝k2／k1，k*2＝k3／k1，计算结果见图3～图5。

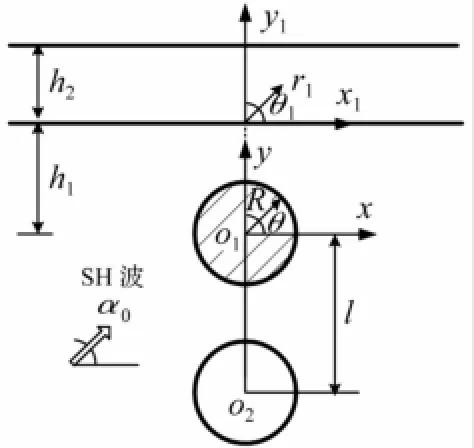
图2 SH波对两纵向相邻圆孔及夹杂入射计算模型Fig．2 Themodel of circular cavity and inclusion locating in same vertical by SH-wave

（1）图3为入射角α0＝90°、h1／R＝1．5、h2／R＝2．0，介质参数k*1与波数k1R不同情况下水平地表位移幅值随X／R的变化。由图3（a）看出，SH波低频入射时夹杂与圆孔及覆盖层的存在对地表位移幅值变化影响较小。由图3（b）、（c）知，SH波较高频入射时在垂直排列的夹杂与圆孔作用下地表位移幅值成对称分布，地表位移沿地表水平方向呈增强、减弱交替震荡且随入射频率增加趋于剧烈。由此可见，中高频垂直入射SH波对地表动位移影响尤其显著。入射SH波与无浅埋结构及无覆盖层半空间地表位移量相比，在圆孔、夹杂及覆盖层共同作用下低频阶段位移被放大，而在中高频阶段减震作用明显。介质参数k*1亦为重要影响因素，k*1增大地表位移幅值减小。

（2）图4为SH波垂直入射、介质参数k*1不同时X／R＝0．0处水平地表位移幅值随h2／R的变化。由图4看出，地表位移幅值随h2／R的增大呈周期性变化，k*1增大引起地表位移震荡频率加大而位移幅值最大值减小。地表覆盖层厚度变化未改变X／R＝0．0处位移幅值最大值，与文献［10］中地表位移幅值与覆盖层厚度无关结论完全一致。

图3 地表位移幅值W（t）随X／R变化Fig．3 Variation of surface displacement amplitudeswith X／R

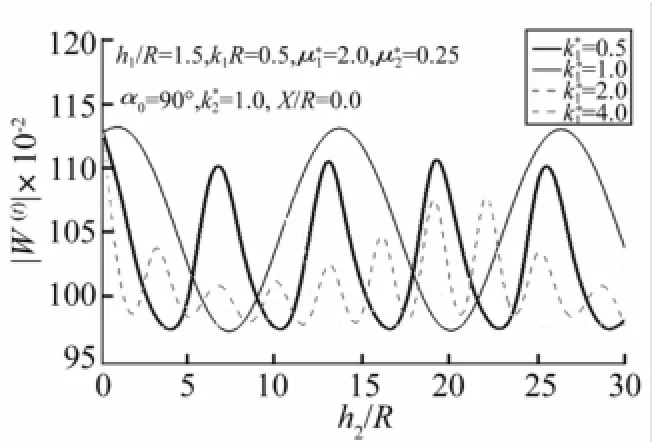
图4 地表位移幅值W（t）随h2／R变化Fig．4 Variation of surface displacement amplitudeswith h2／R

（3）图5为夹杂在埋深、刚度及SH波入射角不同时水平地表位移幅值W（t）随X／R的变化。由图5（a）看出，SH波水平及斜入射时对地表位移影响较大，最大值现于X／R＜0．0范围内，且地表位移在X／R＜0．0时变化幅度较大，震荡效果明显，而浅埋孔洞及夹杂背波面一侧地表位移变化明显减缓，其幅值明显降低。表明浅埋孔洞、夹杂的迎波面对入射波反射其后面区域产生屏蔽，起到隔振作用；由图5（b）看出，埋深增大时圆孔与夹杂对地表位移影响减弱。随埋深h增大地表位移变化趋于平稳。由图5（c）看出，μ*2＝4．0夹杂刚性较大时对地表位移影响变小，与图5（a）相比，地表位移幅值最大值变小。

（4）将本文算例中参数赋予特殊值进行退化验算见图6，结果与文献［11］基本一致。

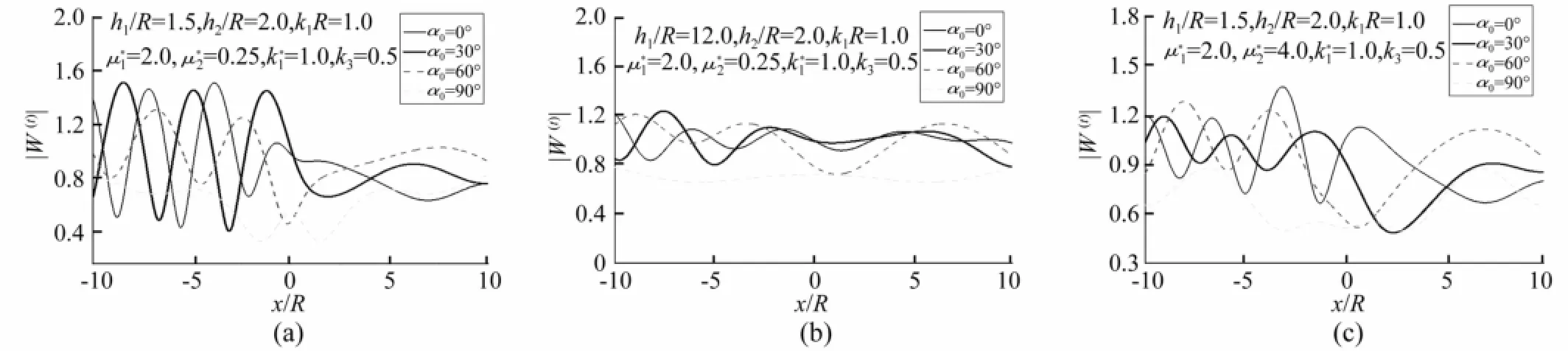
图5 地表位移幅值W（t）随X／R变化Fig．5 Variation of surface displacement amplitudeswith X／R

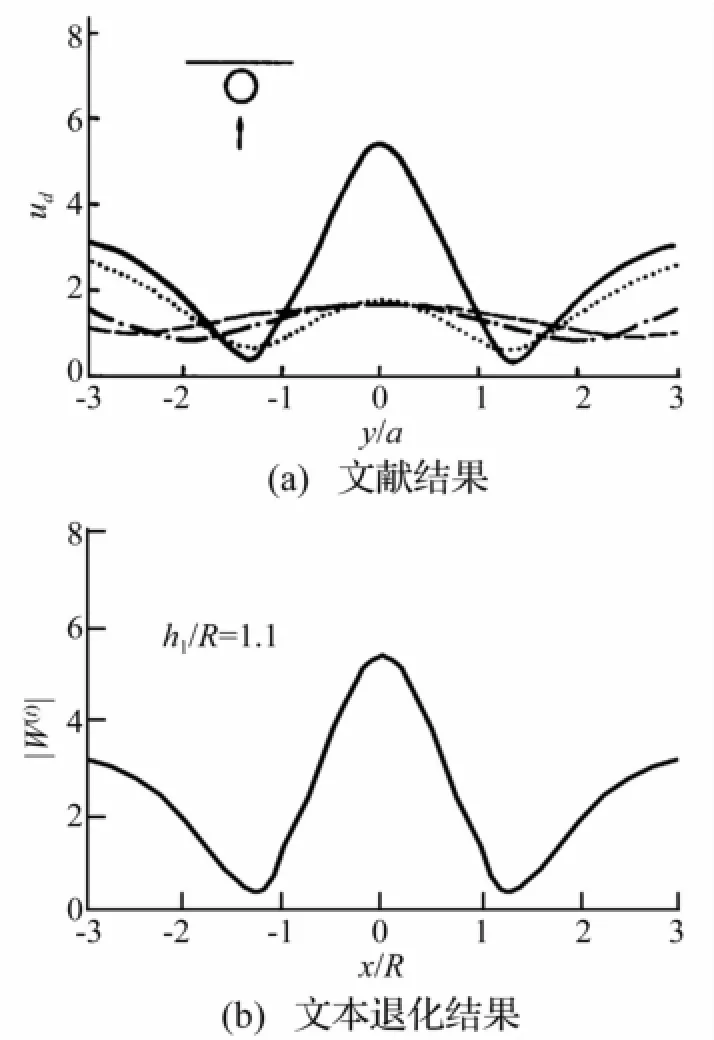
图6 结果对比Fig．6 Results contrast

3 结 论

利用复变函数法及大圆弧假定法给出SH波作用下带地表覆盖层的弹性半空间内圆孔及夹杂散射的近似解析解，探讨、分析地震动变化。数值结果表明，半无限空间中地表覆盖层及夹杂与浅埋孔洞之间存在强烈相互作用，地震动受影响较大。何时产生放大或隔震减震作用与入射波数、埋深、覆盖层及夹杂刚度等介质参数及入射波入射角度等因素密切相关。工程中须对地表覆盖层及隐蔽地形予以重视。

［1］薄景山，李秀领，李山有．场地条件对地震动影响研究的若干进展［J］．世界地震工程，2003，19（2）：11－15．

BO Jing-shan，LIXiu-ling，LIShan-you．Some progress of study on the effect of site conditions on ground motion［J］．World Earthquake Engineering，2003，19（2）：11－15．

［2］梁建文，魏新磊，VincentW LEE．圆弧形沉积谷地对平面P波的三维散射解析解［J］．岩土力学，2010，31（2）：461－470．

LIANG Jian-wen，WEI Xin-lei，Vincent W LEE．3－D scattering of plane P waves by a circular-arc alluvial valley［J］．Rock and Soil Mechanics，2010，31（2）：461－470．

［3］王慧文，刘殿魁，邱发强，等．SH波入射时浅埋圆形结构附近半圆形沉积谷地的地震动［J］．哈尔滨工业大学学报，2006，38（6）：941－945．

WANGHui-wen，LIU Dian-kui，QIU Fa-qiang，etal．Ground motion of semi-cylindrical alluvial valley above subsurface circular structure impacted by SH-waves［J］．Journal of Harbin Institute of Technology，2006，38（6）：941－945．

［4］Yuan Xiao-ming，Men Fu-lu．Scattering of plane SH-wavesby a semi-cylindrical hill［J］．Earthquake Engineering and Structural Dynamics，1992，21（12）：1091－1098．

［5］刘殿魁，林宏．浅埋的圆柱形孔洞对SH波的散射与地震动［J］．爆炸与冲击，2003，23（1）：6－12．

LIU Dian-kui，LIN Hong．Scattering of SH waves by a shallow buried cylindrical cavity and the ground motion［J］．Explosion and Shock Waves，2003，23（1）：6－12．

［6］王慧文，杨在林．SH波入射时多个浅埋圆形衬砌结构附近半圆形沉积层的地表位移［J］．哈尔滨工业大学学报，2011，43（增1）：309－314．

WANG Hui-wen，YANG Zai-lin．The ground surface displacement of a semi-cylindrical alluvial valley above subsurface circular structure impacted by SH-waves［J］．Journal of Harbin Institute of Technology，2010，43（S1）：309－314．

［7］陈志刚，杨在林，刘殿魁．SH波在浅埋椭圆孔上的散射对地震动的影响［J］．哈尔滨工程大学学报，2006，27（1）：5－9．

CHEN Zhi-gang，YANG Zai-lin，LIU Dian-kui．Effect of scattering on the ground motion above a subsurface elliptic cavity by incident SH-waves［J］．Journal of Harbin Engineering University，2006，27（1）：5－9．

［8］梁建文，张季，巴振宁．层状半空间中洞室群对地震动的时域放大作用［J］．土木工程学报，2012，45（增1）：152－157．

LIANG Jian-wen，ZHANG Ji，BA Zhen-ning．Time-domain amplification of seismic ground motion by group cavities in layered half-space［J］．China Civil Engineering Journal，2012，45（S1）：152－157．

［9］Lee V W，Karl J．Diffraction of elastic plane p wave by circular underground unlined tunnels［J］．European Earthquake Engineering，1993，6（1）：29－36．

［10］袁晓铭，李雨润，孙锐．圆弧状沉积盆地与软土单覆盖层出平面地表运动对比［J］．地震工程与工程振动，2002，22（4）：16－21．

YUAN Xiao-ming，LIYu-run，SUN Rui．Comparison of outof-plane surface ground motion between a circular-arc alluvial valley and a single overburden soft layer［J］．Earthquake Engineering and Engineering Vibration，2002，22（4）：16－21．

［11］袁晓铭．地表下圆形夹塞区出平面散射对地面运动的影响［J］．地球物理学报，1996，39（3）：373－381．

YUAN Xiao-ming．Effect of a circular underground inclusion on surfacemotion under incident plane SH-wave［J］．Chinese Journal of Geophysics，1996，39（3）：373－381．

Scattering of SH-wave to subsurface circular cavity and inclusion in a layered half-space and the induced ground motion

QIHui，CHEN Dong-ni，CAILi-ming
（Harbin Engineering University，Aerial and Civil Engineering College，Harbin 150001，China）

The solution of scattering of SH-wave was given by the method using an circular boundary with large radius to approximate the straightboundary of surface layer．In the lightof the theory of Helmholtz，the general solution of the Biot's wave function was achieved．Utilizing the complex function method and the boundary conditions，the present problem was transformed into a problem in which only infinite linear algebraic equationswith unknown coefficients need to be solved．Numerical results of the ground motion were provided．The effects of incident wave number，incident angle，buried depth，stiffness of inclusion and layer on ground motion were analyzed qualitatively．The results of numerical examples show that great a influence on ground motion may occur due to strong interaction between the surface layer and the circular cavity and inclusion．

surface layer；circular cavity；inclusion；scattering of SH-wave；large arc assumed method；ground motion

O343．1；P315．3

：A

10．13465／j．cnki．jvs．2014．22．027

中央高校基本科研业务费项目资助

2013－07－11 修改稿收到日期：2013－11－06

齐辉男，教授，博士生导师，1963年生

陈冬妮女，博士，讲师，1974年12月生