基于灰色-BP神经网络理论的上染率模型研究

徐文龙，汪 澜，张永兴

（浙江理工大学，a.先进纺织材料与制备技术教育部重点实验室；b.机械与自动控制学院，杭州310018）

基于灰色-BP神经网络理论的上染率模型研究

徐文龙a，汪 澜a，张永兴b

（浙江理工大学，a.先进纺织材料与制备技术教育部重点实验室；b.机械与自动控制学院，杭州310018）

以活性黄3RF上染棉织物为例，首先利用灰色系统GM（1，1）和Verhulst建立起上染率-染色工艺单因素模型，再将其输出直接作为神经网络的输入，最终建立灰色-BP神经网络上染率-染色工艺多因素模型，其拟合值的相对误差小于1.3%，并通过实验验证，预测值的误差均在1.0%以内。验证结果表明，该数学模型精确度较高，能较准确地反映棉织物活性染料染色后的上染率，并可以满足预测上染率的需求。

活性染料；棉织物；灰色-BP神经网络；上染率；多因素模型

0 引 言

染料上染率反映了染色过程纤维与染料的结合程度，是衡量染料性能及染色质量的重要指标之一［1］。若能通过染色工艺，控制染色过程和预测上染率，便能达到提高染色产品质量和染料利用率的目的。由于纺织品染色过程中伴随着大量的物理、化学变化，影响染色过程上染率的因素很多，因此上染率建模存在一定难度。

为了实现间歇式染色过程的精确建模，本文采取了将灰色模型和BP神经网络融合的方法。即利用BP神经网络将多个单因素模型融合成多因素模型，同时修正灰色建模的误差。具体步骤是利用GM（1，1）和Verhulst分别建立起上染率-染色工艺单因素模型，再将其输出直接作为神经网络的输入，利用神经网络无限逼近任意函数的能力，再建立上染率-染色工艺多因素模型，进一步提高模型的精度。

1 实验部分

1.1 材料与药品

纯棉平纹织物（75 g/m2）；活性黄3RF（安诺其股份有限公司）；无水硫酸钠（分析纯）；无水碳酸钠（分析纯）。

1.2 实验仪器与设备

IR-12红外染色机（台湾新瑞开发科技有限公司），UV-2550紫外分光光度计（Shimadzu Corporation），DHG-9140A型电热恒温鼓风干燥箱（英博联科技公司），FA2004电子天平（天津市天有利有限公司）等。

1.3 实验及测试方法

1.3.1 染色工艺处方及流程

染色工艺流程见图1。

图1 染色工艺流程

1.3.2 上染百分率的测定

采用残液法测定上染百分率E［2］。

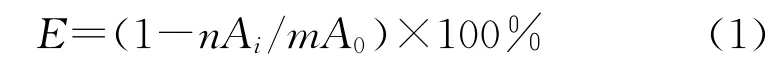
式中：Ai为染后残液稀释n倍后的吸光度；A0为空白染液稀释m倍后的吸光度。

2 结果与讨论

影响上染率的工艺因素有染料浓度、染色温度、染色时间、盐浓度及浴比［3］，由于实际生产过程中一般根据产品色泽的最终要求以及染料特性确定染料的浓度，活性染料的上染时间又分为保温时间和固色时间两个阶段，所以本文仅对染色温度、盐浓度和浴比三个主要工艺因素进行相关分析。

2.1 上染率-染色工艺因素建模

2.1.1 灰色系统建模

灰色系统指信息部分不确定、部分确定，部分不完整、部分完整，部分未知、部分已知的系统［4］，介于白色系统（信息完全确定）和黑色系统（信息完全不确定）之间。灰色模型分为GM（1，1）模型和Verhulst模型。

GM（1，1）模型适合于指数型数据的模型，Verhulst模型要求建模数据是S型的，活性黄3RF的上染率与染色温度的关系数据经过一次累加后属于指数型数据的模型，上染率与盐浓度及浴比的关系数据经过一次累加后属于S型数据的模型。因此，拟使用GM（1，1）模型建立上染率-染色温度工艺因素模型，使用灰色Verhulst模型建立上染率-盐浓度工艺因素模型及上染率-浴比工艺因素模型。

（1）GM（1，1）模型

GM（1，1）适合于指数型数据的模型，此模型可以用于预测，一般用于单因素或者复杂多因素影响的建模，等间隔序列和非等间隔序列都可以建立GM（1，1）模型，其等间隔建模过程如下［5］：首先对原始序列x（0）=（x（0）（1），x（0）（2），x（0）（3），…，x（0）（n））进行一次前向加，即为一次累计值，将x（0）转化为近似指数型数据x（1），有利于减小数据的波动对模型的影响，对x（1）的中值序列进行建模：

因此可将GM（1，1）白化型的解写为：

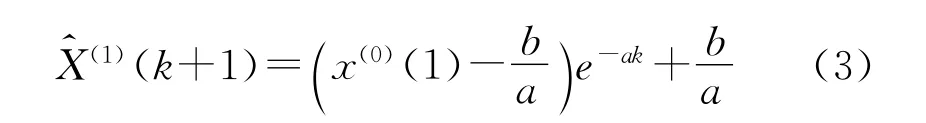
对上染率-染色温度工艺因素使用GM（1，1）模型建模，其参数值为：

a=0.020 608；b=94.313 916。

白化型的解为：

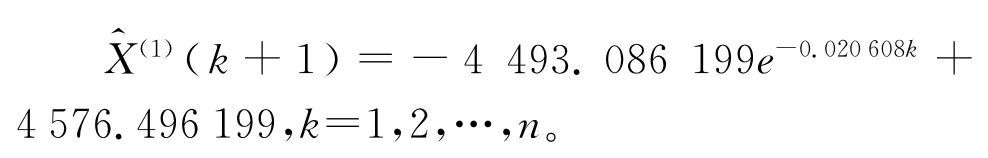
活性黄3RF上染率-染色温度工艺因素模型一次累加值的拟合值及其相对误差如表1所示。

表1 活性黄3RE上染率-染色温度工艺因素模型一次累加值的拟合值及其相对误差

（2）灰色Verhulst模型

灰色Verhulst模型（即GM（1，1，V））要求建模数据是S型的，如果建模数据是单峰型或者不是完全的单峰型，经过累加生成（AGO）后就可以获得较好的S型。此模型可以用来描述诸如一个从生到死的生命过程、一个从发生到饱和的演化过程等。灰色Verhulst模型的建模具体方法如下：对数据的前期处理和GM（1，1）一样，也是建立起x（1）的均值序列z（1），z（1）（k）=0.5x（1）（k）+0.5x（1）（k-1），k=2，3，…，n。

对上染率-盐浓度工艺因素使用灰色Verhulst模型建模，其参数值为：

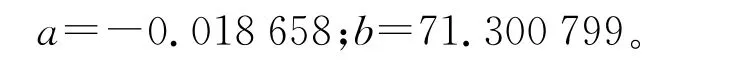
白化响应式为：

活性黄3RF上染率-盐浓度工艺因素模型一次累加值的拟合值及其相对误差如表2所示。

对上染率-浴比工艺因素使用灰色Verhulst模型建模，其参数值为：

白化响应式为：

表2 活性黄3RE上染率-盐浓度工艺因素模型一次累加值的拟合值及其相对误差

活性黄3RF上染率-浴比工艺因素模型一次累加值的拟合值及其相对误差如表3所示。

由表1～表3可知灰色模型部分相对误差较大，指数型数据所建立的模型误差尤为明显，这是由于在求解微分方程的过程中存在很大的误差，并且灰色模型通常用于建立单因素模型。由于单因素模型不能全面反映染色实际情况，为此，下面采取灰色模型与BP神经网络融合的方法来建模。

表3 活性黄3RE上染率-浴比工艺因素模型一次累加值的拟合值及其相对误差

2.1.2 灰色系统与BP神经网络融合建模

BP神经网络是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。它在模拟人脑神经组织的基础上发展起来，是由大量计算单元通过丰富的连接构成的复杂网络，可以实现输入与输出之间的任意线性映射，在函数逼近、模式识别和数据压缩等领域应用广泛［6］。神经网络不需要预先给出公式，而是以实验数据为基础，经过有限次的迭代计算来反映数据间规律的数学模型。网络通过学习，使其输入与期望输出相符，从而达到预测的目的。

采用BP算法的多层前馈网路是至今为止应用最广泛的神经网络，在多层前馈网的应用中，以单隐层网络的应用最为普遍。一般习惯将单隐层前馈网络称为三层前馈网或三层感知器，所谓三层包括了输入层、隐层和输出层。三层前馈网中，输入向量为X=（x1，x2，…，xn）T，图中x0=-1是为隐层神经元引入阈值而设置的；隐层输出向量为Y=（y1，y2，…，yn）T，图中y0=-1是为输出层神经元引入阈值而设置的：输出层输出向量为O=（o1，o2，…，on）；期望输出向量为d=（d1，d2，…，dk，…，dL）T。输入层到隐层之间的权值矩阵为V=（V1，V2，…，Vj，…，Vm），其中列向量Vj为隐层第j个神经元对应的权向量；隐层到输出层之间的权值矩阵用W表示，W =（W1，W2，…，Wk，…，WL），其中列向量Wk为输出层第k个神经元对应的权向量。三层BP网如图2所示。

图2 神经网络拓扑结构图

本文针对染色过程影响因素很多，提出一种灰色-BP神经网络模型，即利用神经网络将染色过程的多个单因素模型融合成一个多因素模型。相对于单因素模型来说，多因素模型能更好地反映染色的真实过程，大幅度提高模型精度。

灰色模型和神经网络的融合有很多种方法：（1）串联型组合，即一方的输出作为另一方的输入，最终的输出结果是整个系统最终的输出结果，用于复杂系统容错分析预测；（2）用神经网络增强灰色系统，构造一个BP网络对灰色微分方程的灰参数进行白化；（3）使用灰色系统辅助构造神经网络；（4）神经网络和灰色系统完全融合。

本文采取的是串联型组合，即将灰色系统的输出作为神经网络的输入，不进行累减操作［7］，直接将灰色系统的输出作为神经网络的输入，这样可以削弱数据的波动性，便于神经网络进行逼近。有利于提高模型精度。本文所用的灰色-BP神经网络模型的拓扑图如图3所示。

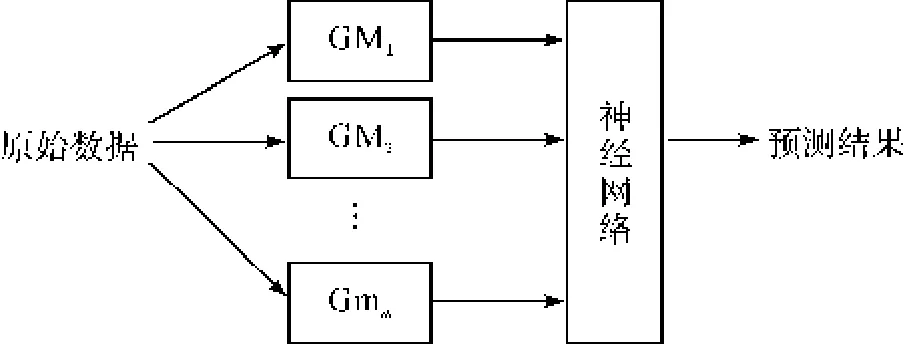
图3 灰色-BP神经网络模型拓扑图

将2.1.1中使用灰色系统建立的上染率-染色工艺单因素模型作为神经网络的输入，不进行累减操作，建立上染率-染色工艺多因素模型，活性黄3RF上染率-染色工艺多因素模型实验值与拟合值的比较如表4所示。

以上拟合值是通过Mat Lab编程得出，采用灰色-BP神经网络理论所建立的上染率-染色工艺多因素模型，其拟合值与实验值的相对误差均小于1.3%，求得实验值与模型拟合值的相关系数为R= 0.998，P=0。相关系数大于0.9，显著性水平小于0.05，说明预测值与实验值吻合性较好，即该模型的拟合度较高。

2.2 上染率-染色工艺多因素模型效果验证

随机抽取三组染色温度、盐浓度及浴比进行实验，对活性染料染棉的上染率-染色工艺多因素模型进行验证。根据模型计算的实验值、预测值及相对误差见表5。

由表5可知，利用活性染料染棉的上染率-染色工艺多因素模型计算的预测值与实验值较为接近，相对误差可控制在1.0%以内。由此表明：该模型可精确预测棉织物活性染料染色过程中不同工艺因素的上染率，切实可用。

表4 活性黄3RE上染率-染色工艺多因素模型实验值与拟合值的比较

表5 活性染料染棉的上染率-染色工艺多因素模型验证结果

3 结 论

将灰色模型与BP神经网络模型相结合，使用灰色系统建立的上染率-染色工艺单因素模型作为神经网络的输入，不进行累减操作，建立活性染料染棉的上染率-染色工艺多因素模型，模型的相对误差在1.3%之内。通过实验验证，所得拟合值与实验值接近，相对误差在1.0%以内。验证结果说明该模型精确度较高，该方法切实可行。

［1］金福江.基于LS-SVM的棉针织物染色上染率模型的研究［J］.福州大学学报：自然科学版，2010，38（3）：446-449.

［2］张 珥，安东东.活性染料上染真丝染色性能的研究［J］.染整技术2010，32（5）：20-23.

［3］赵 涛.染整工艺与原理：下册［M］.北京：中国纺织出版社，2009：85-87.

［4］冯思静，邓元月.中国能源消费预测灰色建模法［J］.数学的实践与认识，2012，42（3）：78-84.

［5］陈正平，苏 虹.灰色系统建模数据的一种变换方法［J］.江苏理工大学学报，1999，20（3）：91-94.

［6］朱海东，刘俊康.改进神经网络-残液法同时测定多组分拼混染料上染率［J］.计算机与应用化学，2009，26（1）：117-120.

［7］熊萍萍，党耀国.灰色Verhulst模型背景值优化的建模方法研究［J］.中国管理科学，2012，20（6）：154-159.

Research on Dye-uptake Rate ModeI Based on Gray-BP NeuraI Network Theory

XU Wen-Long1a，WANG Lan1a，ZHANGYong-xing1b
（a.Key Laboratory of Advanced Textile Materials and Manufacturing Technology，Ministry of Fducation；b.School of Mechanical Fngineering &Automation，Zhejiang Sci-Tech University，Hangzhou 310018）

This paper takes dyeing of cotton fabric with Reactive Yellow 3RF for example.Firstly，dye-uptake rate and dying single-factor model was established with gray system GM（1，1）and verhulst. Secondly，the output directly served as the input of neural network，and finally dye-uptake rate and dying multi-factor model based on gray-BP neural network was established.The relative error of the fitting values was less than 1.3%.The experimental result shows that the error of the predicted value is within 1.0%.The verification results show that the mathematical model has high accuracy and can exactly reflect the dye-uptake rate of reactive dyes in the dyeing process and meet the actual requirement of forecasted dye-uptake rate.

reactive dyes；cotton fabric；Grey-BP neural network；dye-uptake rate；multi-factor model

TS190.9

A

（责任编辑：许惠儿）

1673-3851（2014）04-0343-04

2013-10-30

国家自然科学基金（61074154）

徐文龙（1988-），男，山东德州人，硕士研究生，主要研究方向为生态纺织染整技术及染整污染控制。

汪 澜，F-mail：wlan_cn@aliyun.com