近断层速度脉冲地震动引起的边坡永久位移预测模型

高广运，宋 健

（1.同济大学 地下建筑与工程系，上海 200092；2.同济大学 岩土及地下工程教育部重点实验室，上海 200092）

1 引 言

地震引起的边坡永久位移作为衡量边坡稳定性的重要参数，其准确预测对提高边坡震害区划及灾害性分析的水平具有重要意义。Newmark刚塑性滑块法[1]是目前预测边坡地震永久位移最常用的简化方法，许多学者对其进行了改进和完善[2－4]，用于具体边坡工程的地震稳定性分析及边坡概率地震灾害性分析。

基于边坡永久位移值的概率地震灾害性分析，是求出边坡在一系列可能的地震事件中产生的永久位移超过某一允许值的年平均概率。对一般的非脉冲地震动引起边坡概率地震灾害分析，以一个地震强度参数为例，计算公式如下：

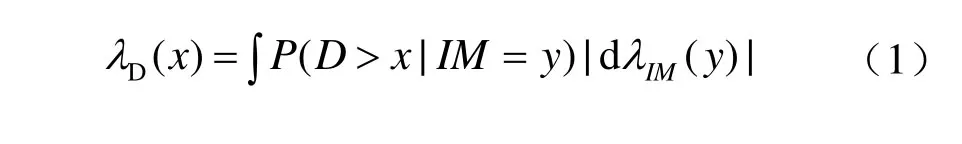
式中：λD(x)为永久位移值超过x的年平均概率；P(D＞x|IM=y)为确定的地震动强度参数y引起的永久位移值超过x的概率，IM 为地震动强度参数；λIM(y)为地震动强度参数超过y的年平均概率，可通过地震动灾害分析曲线得到。上述分析的关键是求出 P(D＞x|IM=y)，这就需要建立永久位移与地震动强度参数的关系，即建立基于地震动强度参数的边坡永久位移预测模型。基于Newmark滑块法，Ambraseys等[5]采用11次地震的50条强震记录，得到了基于峰值加速度PGA的回归方程；Jibson[6]利用30次地震中的2270条地震记录，得到875组计算位移，建立了基于PGA、Arias强度及震级的不同形式的预测模型；Bray等[7]采用41次地震的668条地震记录（每条记录包含两条水平正交的地震动）计算了不同屈服加速度的刚性边坡和不同屈服加速度及自振周期的柔性边坡的滑动位移，并基于此分别得到了适用于刚性、柔性边坡的永久位移预测模型；Rathj等[8－9]基于NGA 数据库的 2383条地震记录，并对加速度-时程数据乘以比例因子2和3，计算得到不同屈服加速度刚性边坡的大约14000个非零永久位移值，分别建立了以多项式形式的永久位移预测模型。总体而言，由于回归数据量的增多以及模型的形式越来越复杂，Rathje和Saygili建立的预测模型离散性最小。

近断层地震动的速度时程常具有大幅值、长周期的强脉冲特性，其对工程结构的危害性远远超过一般的非脉冲地震动[10－12]，且结构动力响应与速度脉冲时程特征参数，如峰值速度PGV相关性较大。理论分析表明，断层破裂的方向性效应是近断层区产生速度脉冲的主要因素，且速度脉冲主要发生在断层法向分量[13－14]。因此，近断层脉冲地震动同样有可能对边坡产生特殊的破坏作用，在动力响应分析及地震灾害评估时，应将脉冲与非脉冲地震动区分对待。Shahi等[15]指出，在进行概率地震灾害分析时，考虑速度脉冲地震动对结构的影响，将对灾害的贡献分为速度脉冲地震动和无脉冲地震动，表示如下：

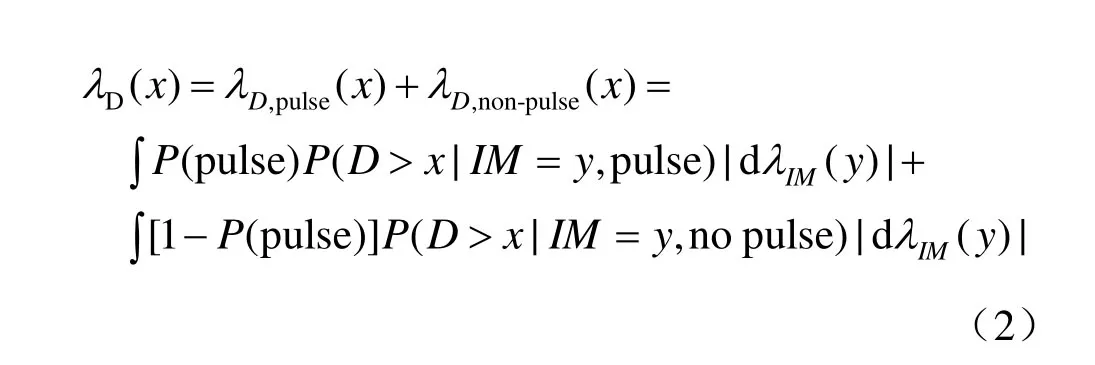
式中：P(pulse)为脉冲发生的概率。因此，要实现上述过程，需要建立基于脉冲地震动强度参数的边坡永久位移预测模型。

本文采用Shahi等[15]提出的脉冲地震动判定方法，从NGA（next generation attenuation）数据库的3551条地震记录中选取出 189条速度脉冲型地震动，地震动均转换成发生最强脉冲的方向（小波系数最大的方向）；基于Newmark方法，将滑坡体简化为刚塑性滑块，分析了近断层速度脉冲地震动作用对边坡永久位移的影响。基于选取的速度脉冲地震动作用下不同屈服加速度刚性边坡的永久位移值，建立了基于PGV的单变量及PGV、PGA的双变量两种永久位移预测模型。本文提出的预测模型为考虑近断层地震动速度脉冲特性影响的边坡永久位移值的概率地震灾害分析提供了基础。

2 速度脉冲地震动的选取

傅里叶频谱分析是将原始地震动信号通过一系列正弦波的线性叠加来代表，可以反映地震动能量在频域内的分布，但不能反映信号频率随时间变化的非平稳性特征。小波分析是一种信号的时间-尺度或时间-频率的分析方法，即将原始信号分解成一系列不同尺度的小波，分别代表不同的频率范围。对于非平稳信号，如地震动信号，它具有高分辨率的特点，而且在时、频域都具有表征信号局部特征的能力，适合分析地震动信号时频变化过程中的瞬态特征。Baker[16]以Db4小波为母小波函数，基于小波分析方法提出了一套脉冲型地震动判定的方法，并从NGA（next generation attenuation）数据库中提取出了91条断层法向分量的速度脉冲记录。然而，要建立合理的近断层速度脉冲引起的边坡永久位移模型，更多的速度脉冲地震动数据是必要的。Shahi等[15]改进了上述方法仅能判别断层法向分量速度脉冲特性的局限性。由于断层破裂模式的不同，脉冲特性不一定只发生于垂直断层方向上，因此，假定地震动小波系数最大的方向为最有可能出现速度脉冲特性的方向，而小波系数最大的方向不一定沿断层法向，只要小波系数最大的方向对应的地震动具有速度脉冲特性，即判定为速度脉冲型地震动。采用上述方法选取的非脉冲地震动（Imperial Valley-06，Bonds Corner）和脉冲地震动（Imperial Valley-06，El Centro Array #4）的速度时程如图1所示。可以看出，相比非脉冲地震动（图1(a)），速度脉冲地震动（图1(b)）在速度时程的开始阶段有一个明显的长周期、大峰值的速度脉冲，且包含了地震动能量的主要部分，因此，可以采用简化的小波脉冲等效原始速度时程。

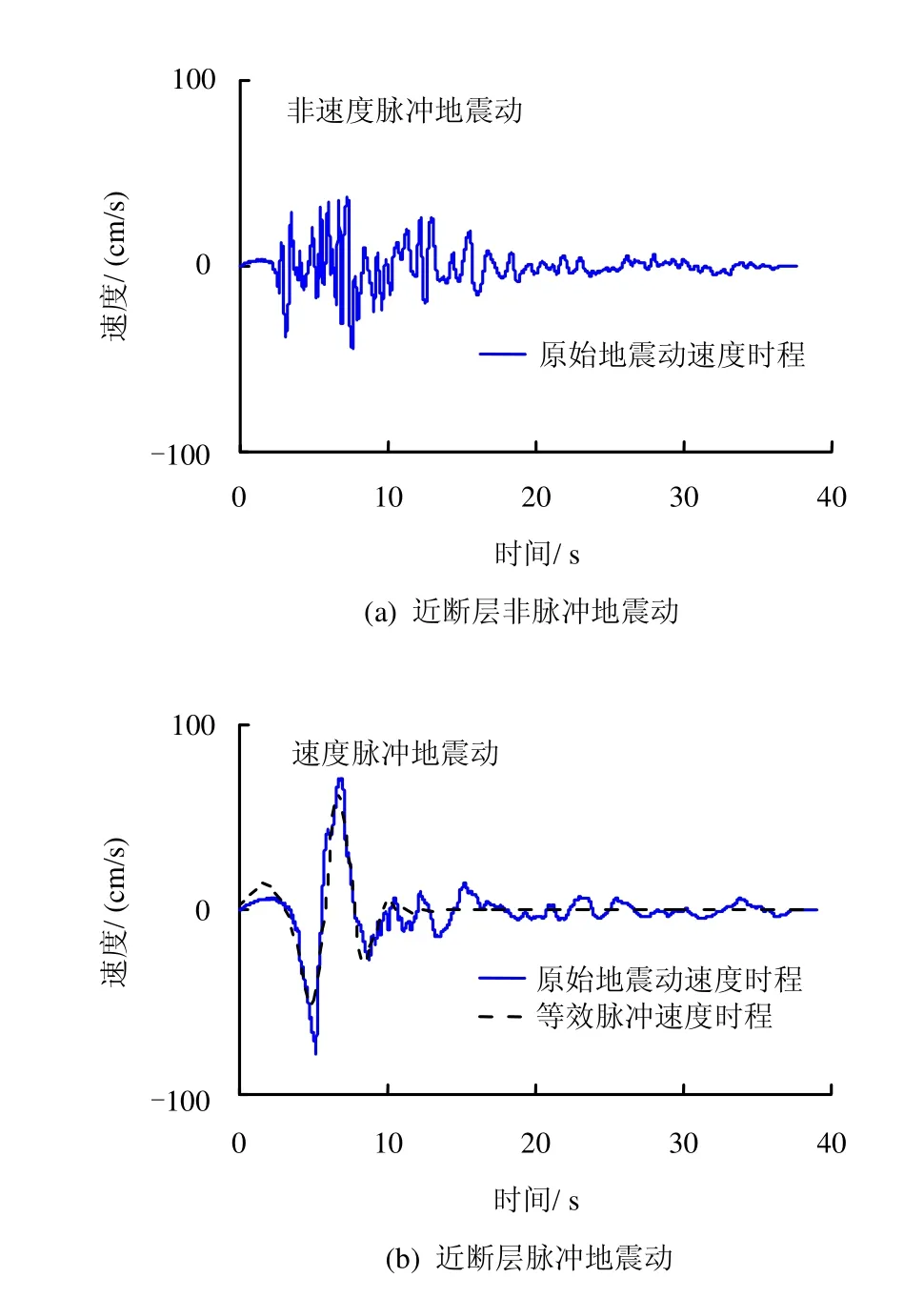
图1 近断层非脉冲地震动和脉冲地震动的速度时程Fig.1 Velocity time histories of near-fault non-pulse and near-fault pulse-like ground motions

基于上述脉冲地震动判定方法，从NGA数据库的3551条地震记录中选取出了189条速度脉冲型地震动记录，为研究近断层地震动速度脉冲特性对边坡永久位移的影响及建立相应的预测模型提供了条件。脉冲地震动分布如表1所示，地震动均转换成发生最强脉冲的方向，即小波系数最大的方向。限于篇幅，具体的地震动记录未能在文中列出。

3 速度脉冲特性的影响

近断层速度脉冲地震动主要由向前方向性效应引起[16]，地震动持时短，速度时程由一系列长周期脉冲成分组成，且PGV值一般较大。本节分别选取32条近断层速度脉冲地震动和32条近断层非速度脉冲地震动，断层距离均在 35 km以内；基于Newmark模型模拟实际边坡，计算得到屈服加速度ky=0.05g时的边坡永久位移时程发展曲线如图 2所示。限于篇幅，具体的地震动记录未能在文中列出。可以看出，速度脉冲地震动引起的永久位移值较大，且滑移主要集中在地震动起始阶段的较短时间内。表2列出了两种类型近断层地震动引起的永久位移的平均值。类似5%～95%地震动持时的计算方法，本文定义5%～95%永久位移发展持时，即滑动位移发展至最终位移值的 5%到最终位移值的95%的时间间隔。可以看出，近断层速度脉冲地震动引起的边坡永久位移值大于非脉冲地震动引起的位移值，且永久位移发展持时较短。导致滑移的坡体具有更大的滑移速度，携带更高的能量，从而对周边环境产生更强的破坏作用。因此，相比于非脉冲地震动，脉冲地震动对边坡产生特殊的破坏作用，表现在最终滑动位移值大、滑动体破坏力强等方面。

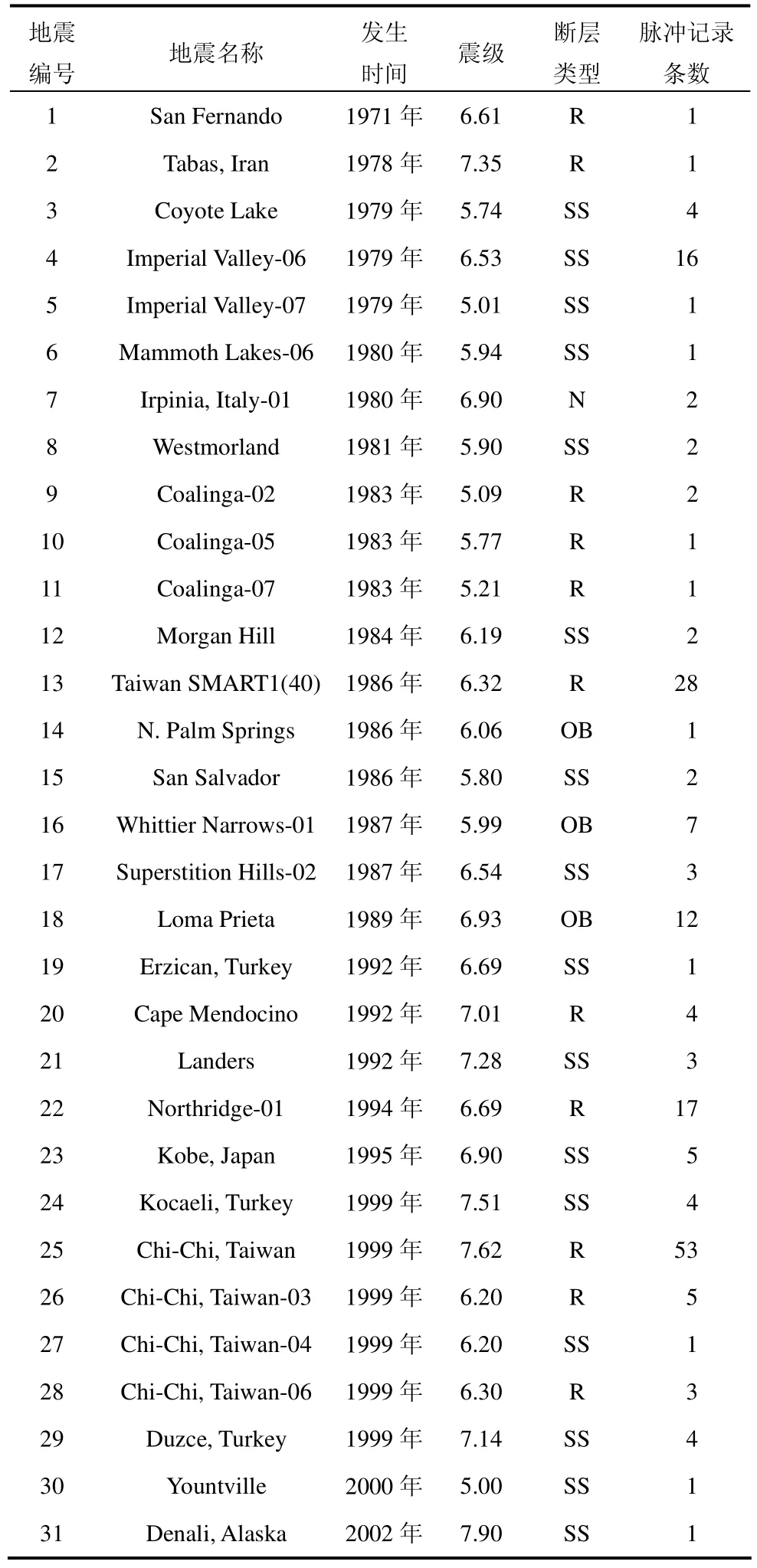
表1 NGA数据库中31个地震事件中的脉冲记录Table 1 Pulse-like records of 31 earthquakes from NGA database

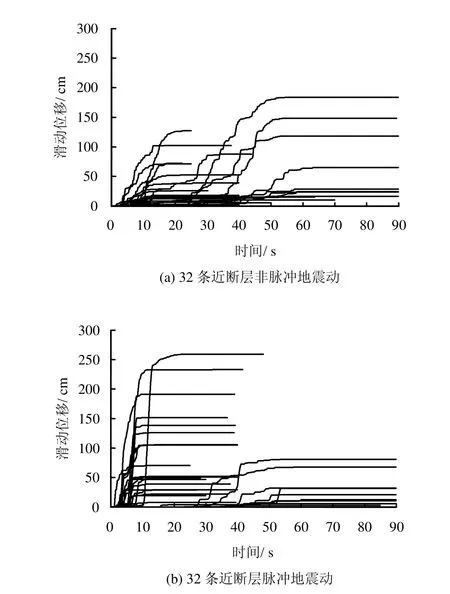
图2 近断层非脉冲地震动和脉冲地震动引起的永久位移时程发展曲线(ky=0.05g)Fig.2 Time histories of permanent displacement caused by near-fault non-pulse and near-fault pulse-like groun d motions(ky=0.05g)

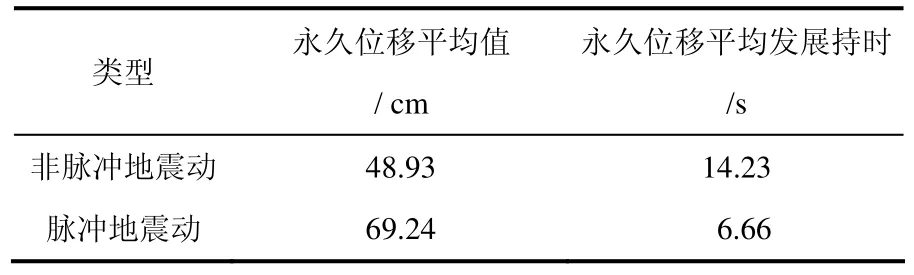
表2 近断层非脉冲和脉冲地震动引起的永久位移平均值Table 2 Mean values of permanent displacement for near-fault non-pulse and pulse-like ground motions

为了更深入地研究脉冲地震动和非脉冲地震动引起边坡永久位移的差别，分别选取非脉冲地震动（Imperial Valley—06，Bonds Corner）和脉冲地震动（Imperial Valley—06，El Centro Array #4）作为输入，计算边坡屈服加速度 ky=0.05g时滑动?体加速度和速度、滑动体沿地面相对速度及相对位移时程发展曲线，如图3所示。可以看出，脉冲地震动引起的永久位移值较大，永久位移发展持时较短是由脉冲地震动特性决定的，大的速度脉冲以及大的地震动峰值速度 PGV导致滑动体沿地面相对速度较大，且呈脉冲形式，从而使最终的永久位移值较大，位移发展持时较短。

4 永久位移预测模型

4.1 既有模型的有效性分析

目前的边坡永久位移预测模型都是基于所有选择的地震动记录建立的，没有区分近场和远场、脉冲和非脉冲地震动，从而增加了预测模型的离散型，降低了模型预测某些特定地震动引起边坡永久位移的准确性。由上节分析可知，脉冲地震动较非脉冲地震动将引起较大的边坡永久位移值。因此，已有的预测模型很可能会低估脉冲地震动引起的永久位移值。下面将对既有永久位移模型的有效性进行分析。

2) 副溶血性弧菌菌落：圆形，边缘整齐，湿润，稍浑浊，半透明，多数具有尖心、斗笠装，蓝绿色菌落，直径为2～4 mm。

取不同的屈服加速度 ky分别为0.02g、0.05g、0.1g、0.2g、0.3g，代表不同强度边坡，利用选取的189条近断层脉冲地震动作为输入，计算得到了742个非零永久位移值。图4为不同的屈服加速度时，对应189条脉冲地震动的永久位移计算值和不同模型预测值的残差（lnD计算值−lnD预测值）的平均值。可以看出，对于任意强度的边坡，Jibson[6]模型和Bray[7]模型均低估了近断层脉冲地震动引起的永久位移值，而Saygili模型则低估近断层脉冲地震动引起的低强度边坡永久位移，高估近断层脉冲地震动引起的高强度边坡永久位移。这是由于Saygili[8]和Rathje[9]建立预测模型时，对加速度时程数据乘以比例因子2和3，人为地提高了地震动的强度，从而大大增加了回归数据中大位移值的比例，导致严重高估了高强度边坡的永久位移（小的位移值）。图5为永久位移和屈服加速度比（ky/PGA）的回归曲线，同时给出了 Jibson[6]模型的预测曲线。同样可以看出，Jibson模型低估了近断层脉冲地震动引起的边坡永久位移。

4.2 基于脉冲地震动参数的永久位移预测模型

通过上述分析可知，既有模型不适用于预测近断层速度脉冲地震动引起的边坡永久位移值。因此，需要考虑近断层脉冲地震动特性，选取合适的地震动参数，建立脉冲地震动引起的永久位移的预测模型。

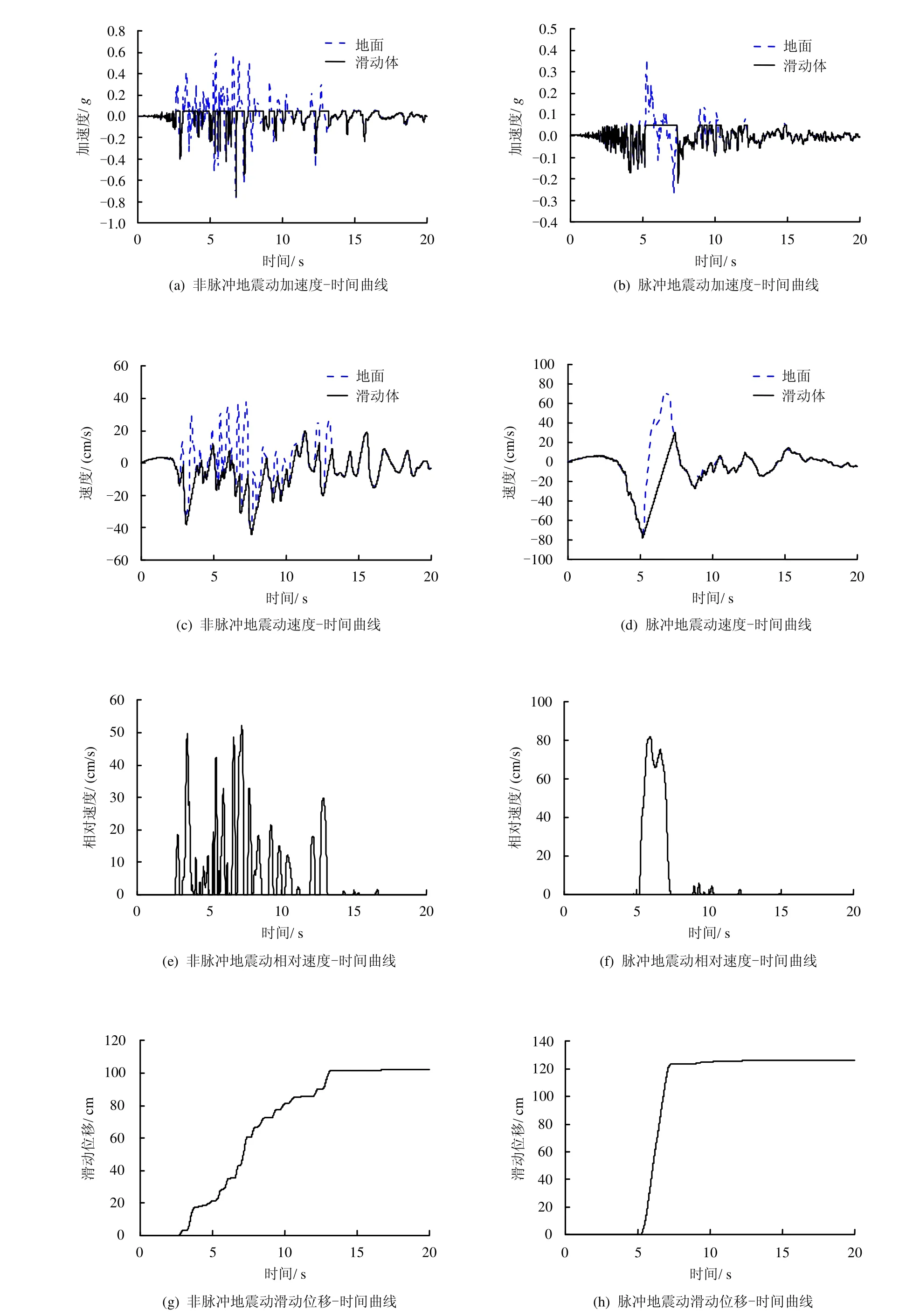
图3 近断层非脉冲和脉冲地震动引起的滑动体加速度、速度和滑动体沿地面相对速度及相对位移时程发展曲线(ky=0.05g)Fig.3 Time histories of permanent acceleration of block,permanent velocity of block,relative velocityand displacement caused by near-fault non-pulse and near-fault pulse-like ground motions(ky=0.05g)

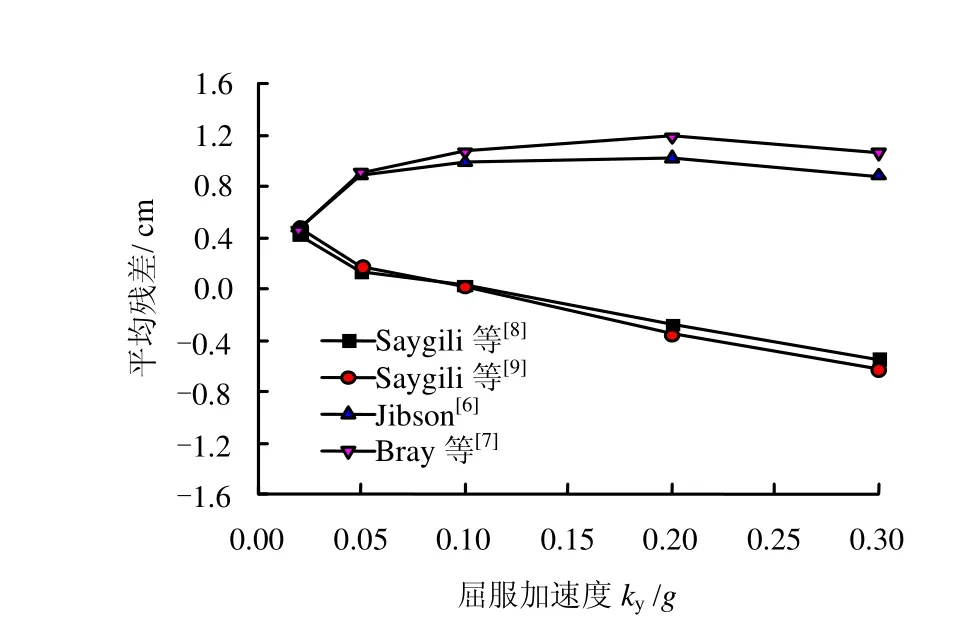
图4 不同模型预测值的残差平均值与屈服加速度ky的变化关系Fig.4 Mean values of the residuals of different predictive models plotted v ersus yield acceleration ky

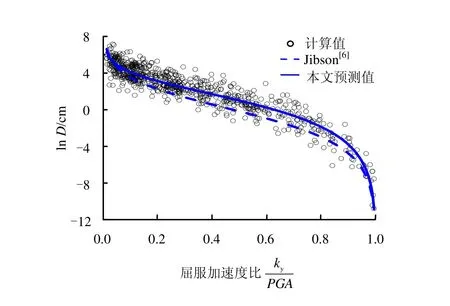
图5 永久位移和ky/PGA的回归曲线Fig.5 Predictive curves of permanent displacements as a function of ky/P GA

4.2.1 地震动参数的选取

既有边坡永久位移预测模型多采用峰值加速度PGA、Arias强度AI为地震动强度参数。近断层速度脉冲地震动的脉冲形式表现在速度时程上，由图3(b)也可以看出，近断层脉冲地震动引起的永久位移主要发生在速度脉冲阶段。因此，地震动速度时程参数也许能够更好地描述脉冲地震动引起的永久位移值。

图6为屈服加速度 ky=0.05g时的189条脉冲地震动引起的边坡永久位移值与PGA、PGV及AI的线性回归关系，可以看出，峰值地面速度 PGV与永久位移值的相关性最好（判 定系数 R2最大，离散值σ最小）；与传统非脉冲地震动引起永久位移值的分析结果不同，Arias强度AI与永久位移值关联度并不高，且 AI的计算较为繁琐；峰值地面加速度与永久位移值的相关性最差。

4.2.2 预测模型的建立

图7给出了742个非零永久位移值与边坡屈服加速度 ky和PGV之比（ky/PGV）的分布关系。可以看出，永久位移值与速度脉冲地震动的峰值速度PGV具有高度相关性，位移值ln D＞1时尤为明显。因此，去除ln D＜1的所有位移，采用ln D＞1的共511个永久位移值，建立基于PGV的永久位移预测模型。为了使模型预测具有更小的离散性，除了ky/PGV外，模型中还增加了PGV一项，回归得预测模型如下：

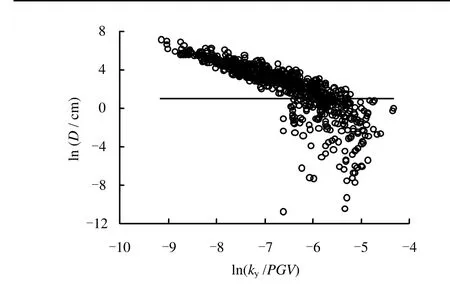
图7 永久位移和ln(ky/PGV)的分布关系Fig.7 Relationship of permanent displacement versus ln(ky/P GV)

判定系数 R2= 0.864，不同屈服加速度对应的永久位移计算值与模型预测值的残差（lnD计算值−lnD预测值）如图8(a)所示，显示了ln D＞1的永久位移与PGV的高度相关性。

小的永久位移值，如ln D＜1，大都发生在 ky较大的边坡，即高强度边坡。由于Newmark方法是计算地震动加速度大于屈服加速度时的位移量，当屈服加速度较大，甚至接近地震动峰值加速度时，产生的永久位移很小，此时主导最终永久位移量的参数是峰值加速度PGA。如果考虑全部的742个非零位移，上述PGV模型中还应再增加含PGA的项，本文采用了 ky/PGV，回归得到的模型如下式：

判定系数 R2= 0.914，不同屈服加速度对应的永久位移计算值与模型预测值的残差如图 8(b)所示，模型预测值与计算值拟合较好。

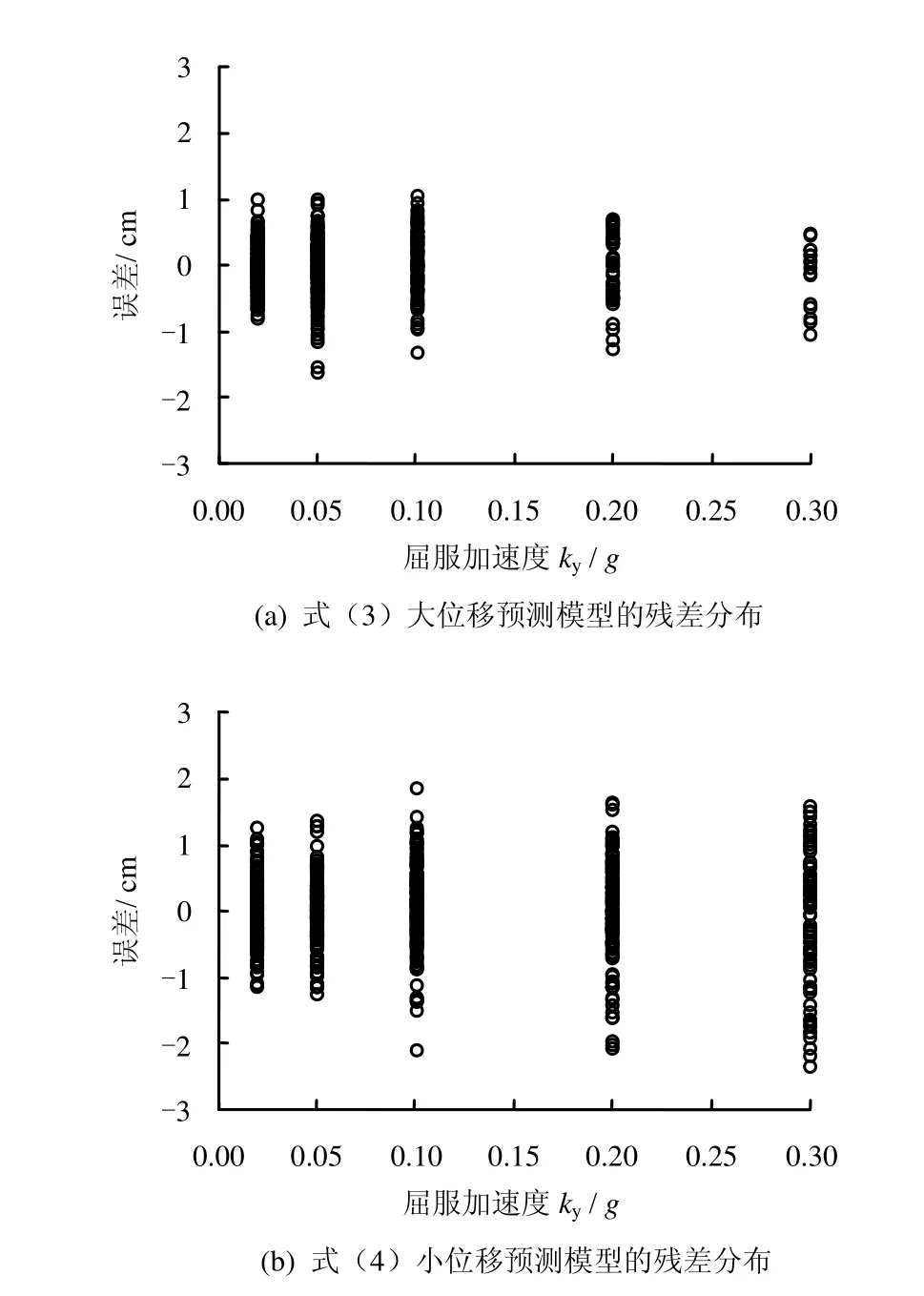
图8 不同屈服加速度ky时方程(3)、(4)的预测值的残差Fig.8 Residuals of Eq.(3) and Eq.(4) plotted versus yield acceleration ky

5 结 论

采用Newmark刚塑性滑块模型，对近断层速度脉冲地震动引起的边坡滑动位移进行分析，并建立了基于速度脉冲地震动参数的两种永久位移预测模型。主要结论如下：

（1）近断层速度脉冲地震动对边坡产生特殊的破坏作用，表现为滑动位移值大、滑动体破坏力强；永久位移值与速度脉冲地震动的峰值速度具有高度相关性，位移值lnD＞1时尤为明显。

（2）既有边坡永久位移预测模型低估了近断层脉冲地震动引起的位移值。因此，本文建立了基于单变量形式的峰值速度及双变量形式的峰值速度、峰值加速度两种永久位移预测模型，模型简单、实用，与回归数据具有很好的相关性，前者更适用于预测对实际工程影响较大的永久位移值（ln 1D＞），且离散性较小。

（3）要建立更为合理的脉冲地震动引起的永久位移预测模型，更多的脉冲地震动记录是必要的，而基于小波分析的脉冲地震动判定方法为今后建立大量的近断层脉冲地震动数据库提供了基础。

（4）本文提出的预测模型为考虑近断层地震动速度脉冲特性影响的边坡永久位移值的概率地震灾害分析提供了基础。

[1]NEWMARK N M.Effects of earthquakes on dams and embankments[J].Geotechnique,1965,15(2): 139－160.

[2]MAKDISI F I,SEED H B.Simplified procedure for estimation dam and embankment earthquake induced deformations[J].Journal of the Geotechnical Engineering Division,ASCE,1978,104(GT7): 849－868.

[3]RATHJE E M,BRAY J D.An examination of simplified earthquake induced displacement procedures for earth structures[J].Canadian Geotechnical Journal,1999,36(1): 72－87.

[4]RATHJE E M,BRAY J D.Nonlinear coupled seismic analysis of earth structure[J].Journal of Geotechnical and Geoenvironmental Engineering,2000,126(11):1002－1215.

[5]AMBRASEYS N N,MENU J M.Earthquake-induced ground displacements[J].Earthquake Engineering and Structural Dynamics,1988,16(7): 985－1006.

[6]JIBSON R W.Regression models for estimating coseismic landslide displacement[J].Engineering Geology,2007,91(2-4): 209－218.

[7]BRAY J D,TRAVASAROU T.Simplified procedure for estimating earthquake-induced deviatoric slope displacements[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(4): 381－392.

[8]SAYGILI G,RATHJE E M.Empirical predictive models for earthquake-induced sliding displacements of slopes[J].Journal of Geotechnical and Geoenviron-mental Engineering,2008,134(6): 790－803.

[9]RATHJE E M,SAYGILI G.Probabilistic assessment of earthquake-induced sliding displacements of natural slopes[J].Bulletin of the New Zealand Society for Earthquake Engineering,2009,42(1): 18－27.

[10]KALKAN E,KUNNATH S K.Effects of fling step and forward directivity on seismic response of building[J].Earthquake Spectra,2006,22(2): 367－390.

[11]江义,杨迪雄,李刚.近断层地震动向前方向性效应和滑冲效应对高层钢结构地震反应的影响[J].建筑结构学报,2010,31(9): 103－110.JIANG Yi,YANG Di-xiong,LI Gang.Effects of forward directivity and fling step of near-fault ground motions on seismic responses of high-rise steel structure[J].Journal of Building Structures,2010,31(9): 103－110.

[12]SEHHATI R,RODRIGUEZ-MAREK A,ELGAWADY M,et al.Effects of near-fault ground motions and equivalent pulses on multi-story structures[J].Engineering Structures,2011,33(3): 767－779.

[13]SOMERVILLE P G,SMITH N F,GRAVES R W,et al.Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J].Seismological Research Letters,1997,68(1): 199－222.

[14]SOMERVILLE P G.Magnitude scaling of the near fault rupture directivity pulse[J].Physics of the Earth and Planetary Interiors,2003,137(2): 201－212.

[15]SHAHI S K,BAKER J W.An empirically calibrated framework for including the effects of near-fault directivity in probabilistic seismic hazard analysis[J].Bulletin of the Seismological Society of America,2011,101(2): 742－755.

[16]BAKER J W.Quantitative classification of near-fault ground motions using wavelet analysis[J].Bulletin of the Seismological Society of America,2007,97(5): 1486－1501.